Похожие презентации:
Векторы в пространстве
1.
Векторы впространстве
2.
Цели урока• Знать: определение вектора в
пространстве и связанные с
ним понятия; равенство
векторов
• Уметь: решать задачи по
данной теме
3.
Физические величиныСкорость v
Ускорение а
Перемещение
Сила F
s
4.
Электрическое полеЕ
+
5.
вНаправление тока
Магнитное поле
6.
Понятие вектора появилось в 19 веке вработах математиков
Г. Грассмана
У. Гамильтона
7.
Современная символика для обозначениявектора r была введена в 1853 году
французским математиком О. Коши.
8.
ЗаданиеПовторить все термины по теме «Векторы на
плоскости»
Вектор
Нулевой вектор
Длина вектора
Коллинеарные векторы
Сонаправленные векторы
Противоположно направленные
векторы
Равенство векторов
9.
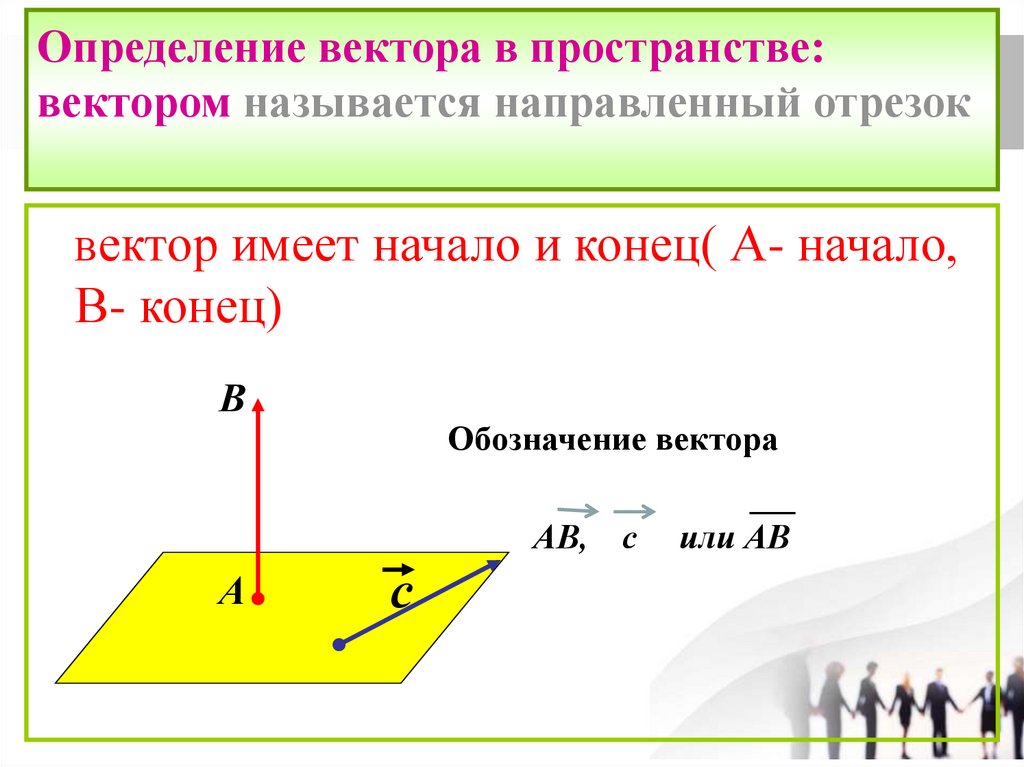
Определение вектора в пространстве:вектором называется направленный отрезок
Вектор
имеет начало и конец( А- начало,
В- конец)
В
Обозначение вектора
АВ,
А
с
с
или АВ
10.
Любая точка пространства такжеможет рассматриваться как вектор. Такой вектор
называется нулевым
0
Т
Обозначение нулевого
вектора
ТТ, 0
11.
ОпределениеКоординатами вектора с началом в точке А1
(х1; у1; z1) и концом в точке
А2 (х2; у2; z2 ) называются числа
х2 - х1, у2 - у1, z2 - z1
Обозначают: А1 А2 ( а1; а2; а3 ) или
а ( а1; а2; а3) или ( а1; а2; а3 ) или
а ( а1; а2; а3)
12.
Решить задачу № 1образец наследующем слайде)
Даны четыре точки
А(1; 2; 3), С(2; 3; 4),
В(4; 5; 6), Д(7; 8; 9)
• Найти координаты векторов АВ, СД,
ВД, АД, ДС,СВ
13.
Образец решенияА(1; 2; 3),
В(4; 5; 6)
АВ = (4 - 1; 5 - 2; 6 - 3) = (3; 3; 3)
Из координат конечной точки
вычитаем координаты начальной точки
14.
Длина ненулевого вектора• Длиной вектора АВ с кординатами (а1;а2;а3) или
абсолютной величиной называется длина отрезка
АВ
• Длина вектора АВ (вектора а) обозначается
так:
АВ , а
• Длина нулевого вектора считается равной
нулю:
0 =0
15.
Абсолютная величинавычисляется по формуле
АВ а1 а2 а3
2
2
2
16.
Решить задачу• Даны две точки А(1;2;3) и
В(2;3;4). Найти длину вектора АВ
Далее образец решения
17.
Образец решения:Сначала найдём координаты вектора:
АВ = (2-1;3-2;4-3) = (1;1;1). Затем по
формуле, найдём модуль
АВ
а1 а2 а3
2
2
2
АВ 12 12 12 3 1,7
18.
Решитьзадачу(самостоятельно)
Даны точки С(2;2;3) и
Д(5;3 ;4),М(5;4;7), К(8;3;5) Найти
длину векторов СД и МК
19.
Определение коллинеарностивекторов
• Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых
20.
Коллинеарные векторыСонаправленные
векторы
Противоположно
направленные
векторы
21.
Какие векторы на рисунке сонаправленные?Какие векторы на рисунке противоположно
направленные?
Найти длины векторов АВ; ВС; СС1.
Сонаправленные векторы:
D1 5 см
C1
AA1 BB1, A1D B1C
3 см
AB D1C1
В1
A1
Противоположно-направленные:
9 см
9 см
CD D1C1, CD AB,
C DA BC
D
A
5 см
3 см АВ = 5 см; ВС = 3 см; ВВ1 = 9 см.
B
22.
•Далее нерассматривать.Дальше будет тема
следующео урока
23.
Равенство векторовВекторы называются равными, если они
сонаправлены и их длины равны
С
В
АВ=ЕС, так как
АВ ЕС и АВ = ЕС
Е
А
24.
Могут ли быть равными векторы на рисунке?Ответ обоснуйте
• Рисунок № 1
А
В
Рисунок № 2
О
Н
К
М
С
АВ=СМ, т. к АВ = СМ
А
АН=ОК, т. к АН ОК
25.
• Среди векторов найдитеравные
АВ = (1; 2; 3)
ВС=(2; 2; 3)
СД=(1; 2; 5)
МК=(1; 2; 3)
АВ = МК
26.
Решить задачуДаны точки: А = (1;2;-3), В=(2;-2;3),
С=(1;-2;5), К=(1;2;3), М=(5;6;7),
Д(0;2;-1)
Найти векторы: АВ, ВС, КМ, ДС и
найти среди них равные
27.
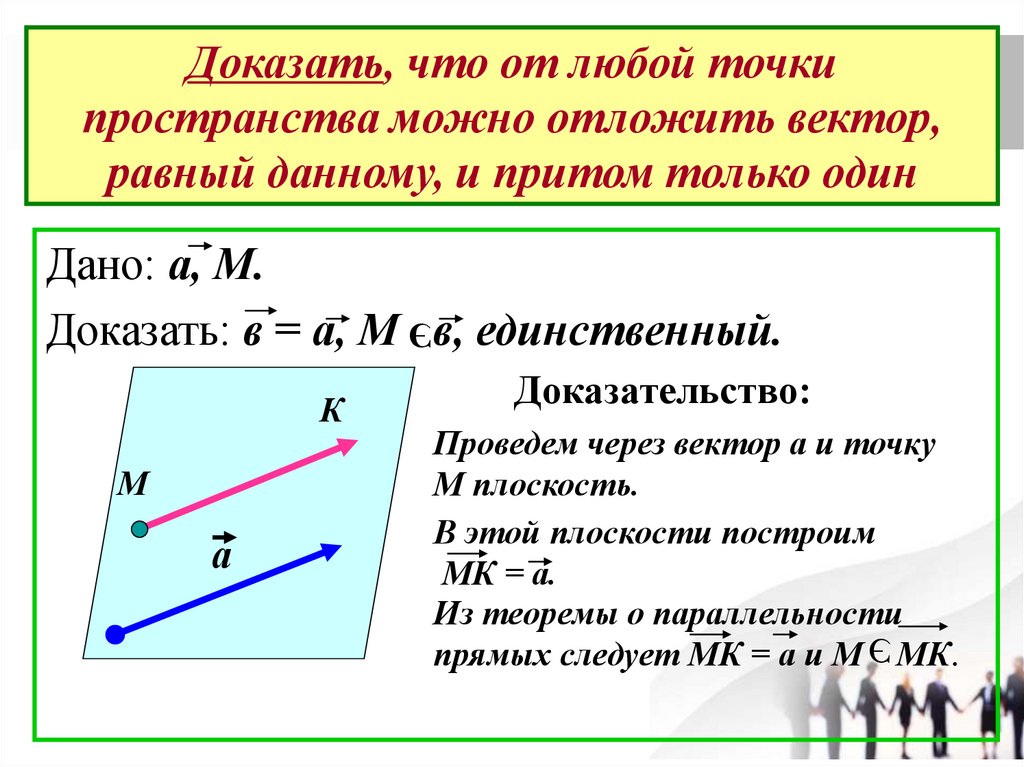
Доказать, что от любой точкипространства можно отложить вектор,
равный данному, и притом только один
Дано: а, М.
Доказать: в = а, М в, единственный.
Э
М
а
Проведем через вектор а и точку
М плоскость.
В этой плоскости построим
МК = а.
Из теоремы о параллельности
прямых следует МК = а и М МК.
Э
К
Доказательство:
28.
• ДАЛЬШЕ НЕ РАЗБИРАЕМ29.
Решение задач№ 322
М
В1
А1
К
С1
Д1
Укажите на этом рисунке
все пары:
а) сонаправленных векторов
ДК и СМ; CВ и С1В1 и Д1А1;
б) противоположно направленных
векторов
СД и АВ; АД и СВ; АА1 и СС1;
С АД и Д1А1; АД и С1В1;
в) равных векторов
А
Д
CВ = С1В1; Д1А1 = С1В1; ДК=СМ
30.
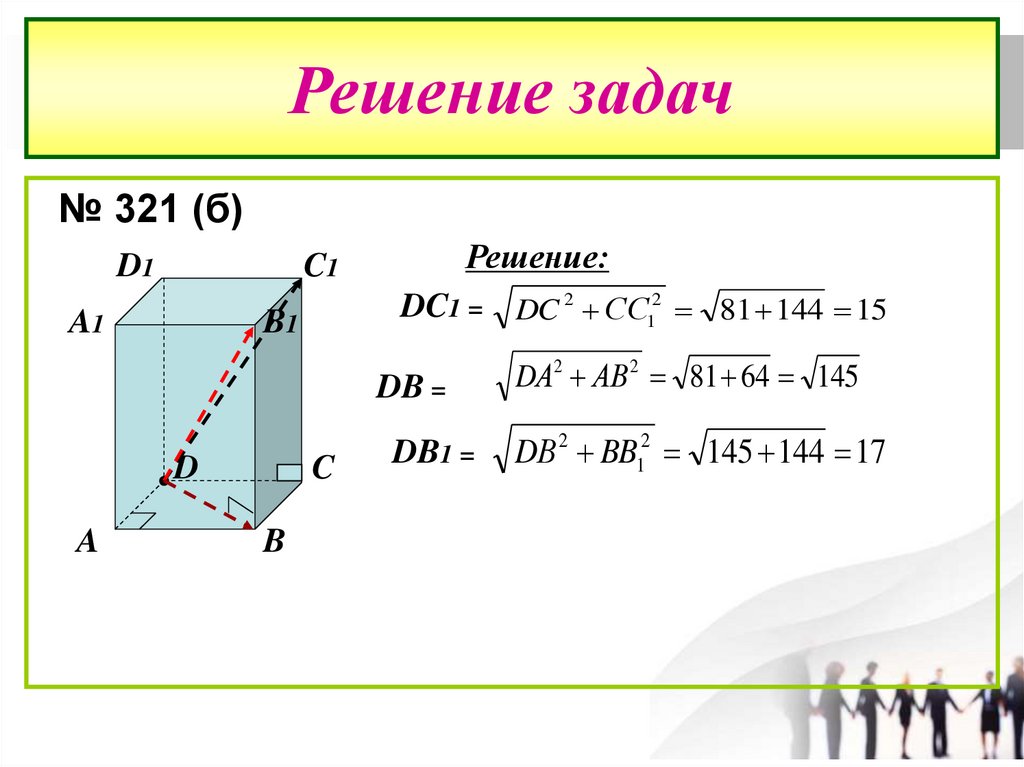
Решение задач№ 321 (б)
D1
Решение:
C1
A1
DC1 = DC 2 СС12 81 144 15
B1
DB =
D
A
C
B
DB1 =
DА2 АВ 2 81 64 145
DВ 2 BB12 145 144 17
31.
Решение задач№ 323
N
А
М
Дано: точки М, N, P,Q – середины сторон
D AB, AD, DC, BC; AB=AD= DC=BC=DD=AC;
а) выписать пары равных векторов;
MN = QP; PN = QM; DP = PC;
б) определить вид четырехугольника
Р MNHQ .
Решение: NP-средняя линия треугольника
ADC, NP = 0,5AC, NP\\AC;
MQ-средняя линия тр. ABC, MQ = 0,5AC,
С MQ\\AC, NP=MQ, NP\\MQ.
PQ-средняя линия треугольника DВC;
Q PQ = 0,5DB, PQ\\DB;
NM-средняя линяя треугольника ADB,
MN = 0,5DB, MN\\DB, PQ=MN, PQ\\MN.
32.
По условию все ребра тетраэдра равны, то онправильный и скрещивающиеся ребра в нем
перпендикулярны.
DB перпендикулярно АС .
MNPQNP=MQ=PQ=MN
NP\\MQ
квадрат
MN\\PQ
33.
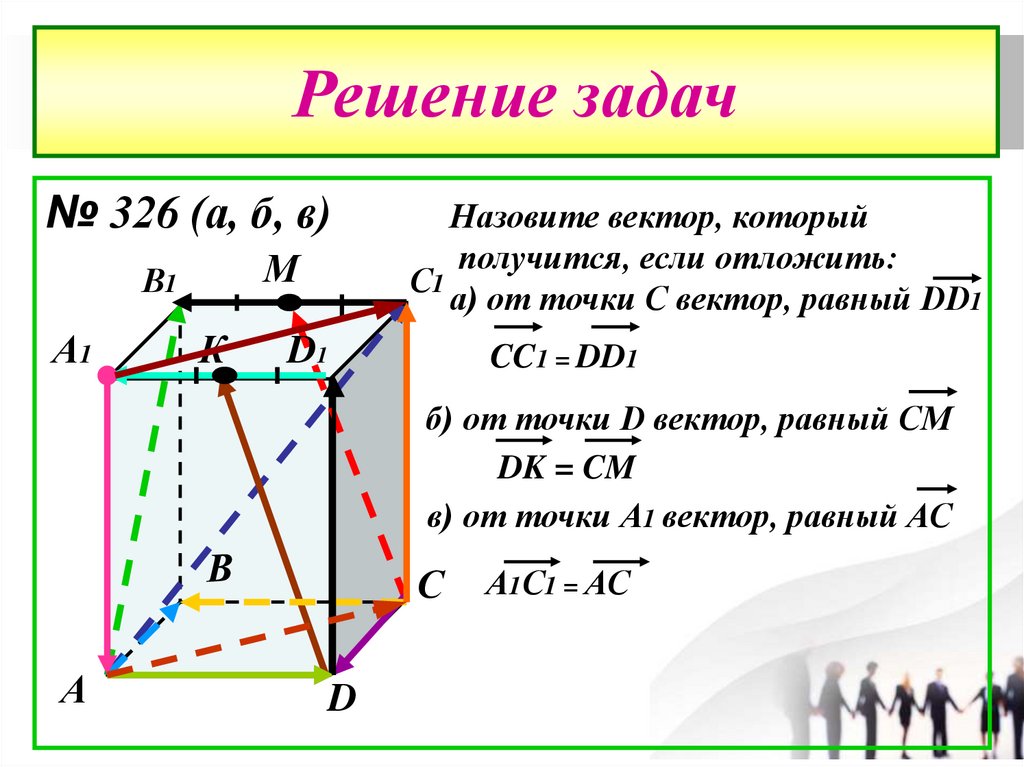
Решение задач№ 326 (а, б, в)
М
В1
А1
К
Назовите вектор, который
получится, если отложить:
С1
а) от точки С вектор, равный DD1
D1
CC1 = DD1
б) от точки D вектор, равный СМ
DK = CM
в) от точки А1 вектор, равный АС
С
А
D
А1С1 = АС
34.
Самостоятельная работаДан тетраэдр МАВС, угол АСВ прямой. Точки К и Р
середины сторон МВ и МС, АС = 9 см и ВА = 15 см.
Найти КМ .
Решение:
Треугольник АВС, угол АСВ- прямой.
М
М
По теореме Пифагора
К
9
А
15
В
С
ВС АВ2 АС 2 225 81 12
КМ – средняя линия треугольника МВС,
КМ = 0,5ВС = 6 см.
КМ = 6 см.
35.
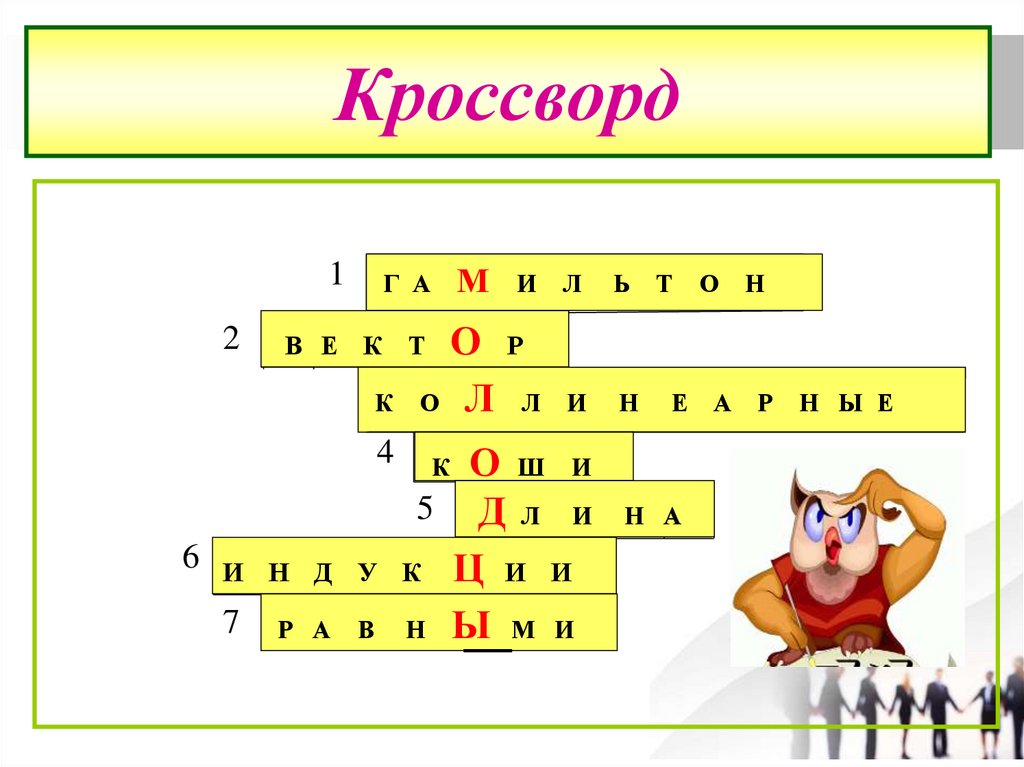
Кроссворд2
1
Г А
В Е
К Т
К
4
6
И Н Д У
7
Р А В
М
О
О Л
И
Л
Ь Т О Н
И
Н
Р
Л
О Ш И
5 Д Л И
К Ц И И
Н Ы М И
Е А Р
К
Н А
Н Ы Е
36.
Домашнее заданиеСтр. 84 – 85
№ 320, 321(а), 325.




























 Математика
Математика








