Похожие презентации:
Применение метода перемещений для расчета колебаний систем с несколькими степенями свободы (применение МКЭ). Семинар 7
1.
Семинар 7. Применение метода перемещений для расчета колебаний систем снесколькими степенями свободы (применение МКЭ)
2.
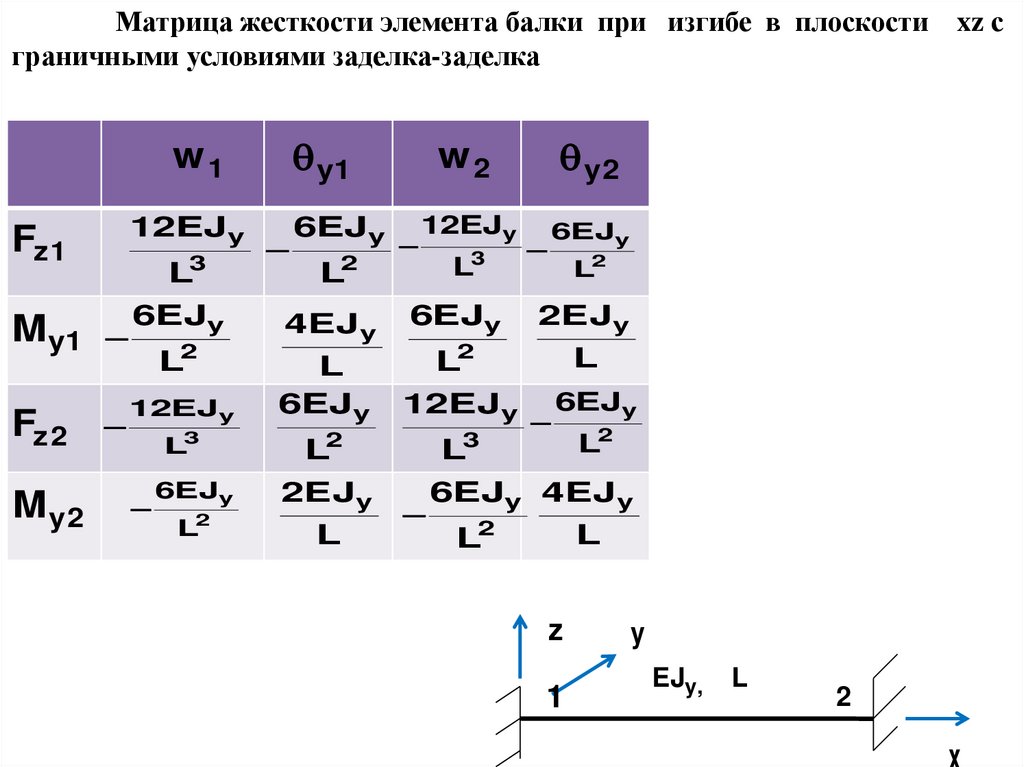
Матрица жесткости элемента балки при изгибе в плоскости xz сграничными условиями заделка-заделка
Fz 1
w1
y1
12EJy
6EJy
L3
y
My1 6EJ
2
L
Fz 2
My2
L2
4EJy
12EJy
L3
6EJy
L2
6EJy
2EJy
L2
L
12EJy
L
6EJy
12EJy
L3
L2
L3
6EJy
2EJy
L2
L
y2
w2
6EJy
L2
6EJy 4EJy
L2
L
z
1
y
EJy,
L
2
3.
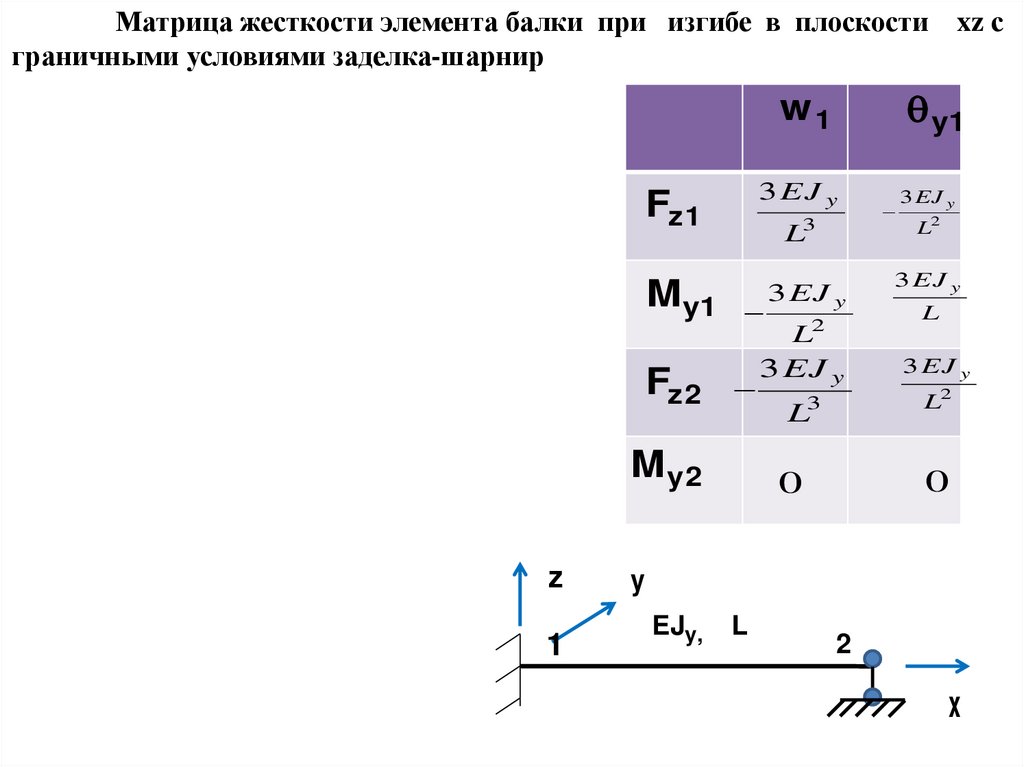
Матрица жесткости элемента балки при изгибе в плоскости xz сграничными условиями заделка-шарнир
y1
w1
Fz 1
3 EJ y
M y1
3 EJ y
Fz 2
L3
My2
z
1
2
3 EJ y
L2
3 EJ y
L
L
3 EJ y
3 EJ y
3
L2
L
0
0
y
EJy,
L
2
x
4.
Таблица изгибающих моментов ипоперечных сил метода перемещений
5.
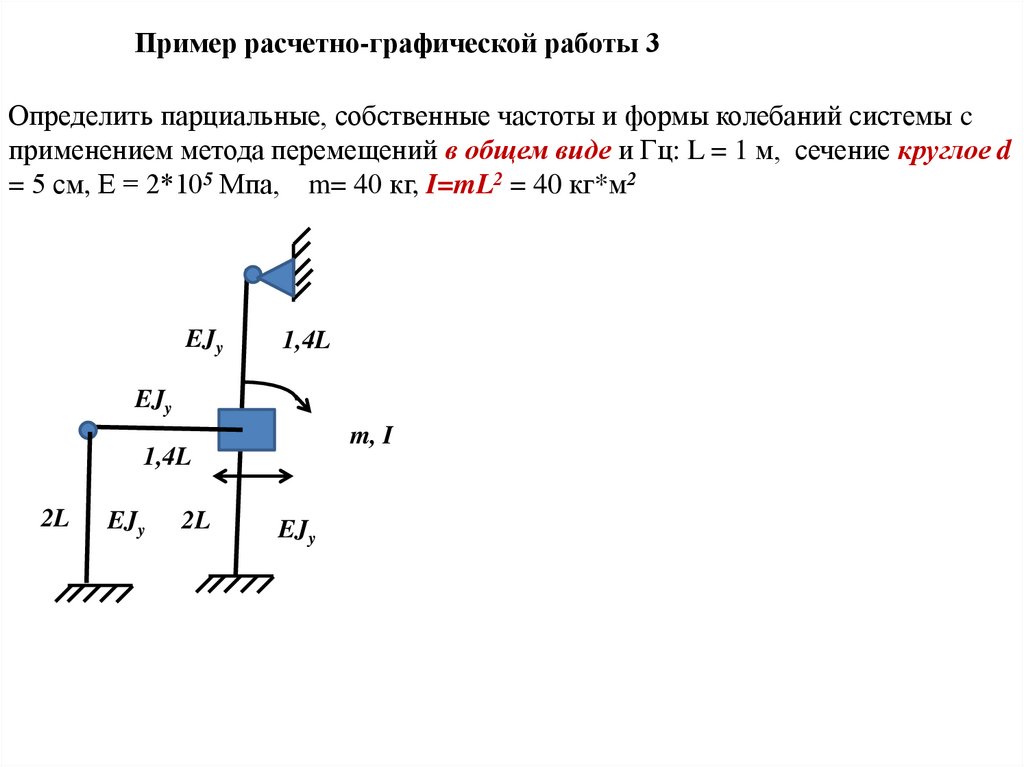
Пример расчетно-графической работы 3Определить парциальные, собственные частоты и формы колебаний системы c
применением метода перемещений в общем виде и Гц: L = 1 м, сечение круглое d
= 5 см, Е = 2*105 Мпа, m= 40 кг, I=mL2 = 40 кг*м2
EJy
1,4L
EJy
m, I
1,4L
2L
EJy
2L
EJy
6.
Уравнения колебаний системы с двумя степенью свободы через жесткостиКинетическая и потенциальная энергии системы равны соответственно
1
(m11 q 12 2m12 q 1q 2 m22 q 22 ),
2
1
U (k11 q12 2k12 q1q2 k 22 q 22 )
2
T
d дT
д
(
)
(T U ) 0
dt дq i
дqi
1 m 12q
2 k11 q1 k12 q2 0
m 11q
1 m 22q
2 k 21 q1 k 22 q2 0
m 21q
(i 1, 2)
7.
или в матричной записиKq 0
Mq
q (t ) v e
i t
( 2 M K ) v 0
Характеристическое уравнение
k11
K
k21
k11
k
21
K 2 M 0
k12
m11
M
k22
m21
k12
m
2 11
k 22
m21
m12
;
m22
m12
k11 2 m11 k12 2 m12
0
2
2
m22
k 21 m21 k 22 m22
Характеристическое уравнение
2
(m 11m 22 m12
) 4 (m 11k22 m 22k11 2m12k12 ) 2 k11k22 k122 0
8.
Определить собственные и парциальные частоты и формы колебаний системы cприменением метода перемещений в общем виде и Гц: L = 1 м, сечение круглое d
= 5 см, Е = 2*105 Мпа, m= 40 кг, I=mL2 = 40 кг*м2
k11
EJy
12 EJ y
1,4L
EJy
m, I
1,4L
2L
EJy
2L
EJy
k22
( 2 L)
3
4 EJ y
2L
k12 k21
3EJ y
( 2 L)
3
3EJ y
1,4 L
6 EJ y
( 2 L)
2
3EJ y
(1,4L)
3EJ y
1,4 L
3EJ y
(1,4 L)
EJ y
2,45 3
m 0
L
M
;
K
2
0
mL
EJ y
3 L2
2
3
2,45
6,28
3
EJ y
L3
EJ y
L
EJ y
L2
EJ y
3 2
L
EJ y
6,28
L
2
(m 11m 22 m12
) 4 (m 11k22 m 22k11 2m12k12 ) 2 k11k22 k122 0
9.
EJ y 2m L ( m 6,28
mL 2,45 3 ) (2,45 6,28 9)( 2 ) 0
L
L
L
2 2
EJ y
4
EJ y
2
2
2
EJ y
2 4,37 3 6,39 3 0
mL
mL
EJ y
4
4 2b 2 c 0
2
2 b b 2 c
2
EJ y
EJ y
2
4,37 3 4,37 3 6,39 3
mL
mL
mL
EJ y
4,37
2
EJ y
3
mL
3,57
2
EJ y
mL3
2
EJ y
f2
53 Гц
2 10 3,14 1*10
2 7,94 3 7,94
333 1 / с
2
3
mL
40 1
64
1
11
4
f1
16, 9 Гц
EJ y
2 10 3,14 1*10
2
1 0,8 3 0,8
106 1 / c
3
4
11
mL
40 1
64
10.
EJ yEJ y
3 2
2,45 3
m 0
L
L
M
;
K
2
EJ y
0
mL
EJ y
6,28
3 L2
L
Парциальные частоты
I
k11
m11
II
k 22
m22
2 1011 3,14 1*10 4
I 2,45 3 2,45
177 1 / c
3
mL
40 1
64
EJ y
I 177
fI
29, 5 Гц
2 6 , 28
2 1011 3,14 1*10 4
II 6,28 3 6,28
290 1 / c
3
mL
40 1
64
EJ y
II 290
f II
46 Гц
2 6 , 28
11.
Парциальные собственные частоты колебанийfI
I 177
29, 5 Гц
2 6 , 28
f II
II 290
46 Гц
2 6 , 28
Собственные частоты колебаний связанной системы
2 333
f2
53 Гц
2 6 , 28
106
f1 1
16, 9 Гц
2 6 , 28
1
I
II
2
Определение собственных форм колебаний связанной системы
12.
Запишем развернутые алгебраические уравнения свободных колебанийk11
k
21
k12
m
2 11
k 22
m21
m12 v11
0
m22 v12
Подставляем все коэффициенты k и m из матриц
EJ y
2,45 3
L
EJ
3 2 y
L
EJ y
3 2
L 2 m
EJ y
0
6,28
L
0 v11
0
2
mL v12
EJ y
EJ y
2
2,45
m
v
3
v
11
12
2
L3
L
0
EJ y
EJ y
2
2
6,28
mL v12
3 L2 v11
L
13.
EJ yEJ y
2
2,45 3 m v11 3 2 v12 0
L
L
EJ y
EJ y
2
2
3 2 v11 6,28
mL v12 0
L
L
Подставляем выражение в общем виде
0,8
2
1
EJ y
EJ y
EJ y
2,45 3 0,8 3 m v11 3 2 v12 0
L
mL
L
EJ y
EJ y
EJ y
2
3 2 v11 6,28
0,8 3 mL v12 0
L
L
mL
1,65
v11 3v12 0
L
3
v11 5,48v12 0
L
EJ y
mL3
14.
1,65v11 3v12 0
L
3
v11 5,48v12 0
L
Решение системы однородных алгебраических уравнений определитель,
которой равен нулю определяется с точностью до постоянного значения: поэтому
положим v12 = 1 и подставим в 1-е уравнение, находим v11 =1,86L
15.
Задание для самостоятельной работыFemap Nx NASTRAN for Windows
Рассчитать 10 первых собственные частоты и формы колебаний секции моста:
Длина двух двутавровых лонжеронов - 50,60,70,80,90,100 м;
Двутавровые лонжероны:
Высота – 1,4; 1,6; 1,8; 2,0; 2,2; 2,4 м ;
Ширина 0,7; 0,8; 0,9; 1,0; 1,1; 1,2 м;
Толщина листа - 0,04 м.
Расстояние между лонжеронами 8 м.
Лонжероны соединены 11 поперечинами квадратного сечения 1х1 м толщиной
листа 0,04 м.
По краям жесткое защемление по всем степеням свободы.
Предварительно оценить прогиб под собственным весом.
E= 2*10^11 н/м^2; м=0.3; G=0,8*10^11 н/м^2;
p= 7850 кг/м^3












 Физика
Физика Механика
Механика








