Колебания систем с одной степенью свободы

1.

Семинар 4. КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ

2.

Рассмотрим изгибные колебания стержня с массой М на конце
L = 2 м, сечение прямоугольное шириной b = 5 см и высотой h = 3 см,
Е = 200 000 Мпа, М = 50 кг
Уравнение для определения собственных частот колебаний
k m 0
2
1 2m f 0
где f = 1/ k - единичная податливость, величина обратная жесткости
Определим единичную податливость методом сил

3.

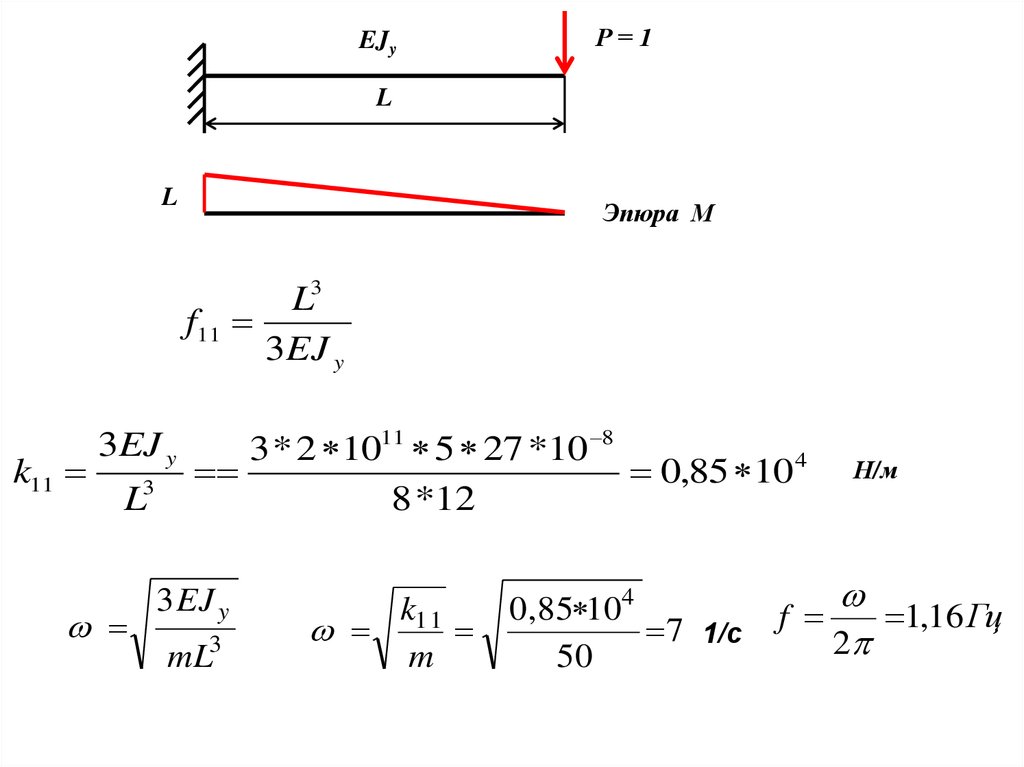
EJy
Р=1
L
L
Эпюра М
L3
f11
3EJ y
k11
3EJ y
3
L
3 * 2 1011 5 27 *10 8
0,85 10 4
8 *12
3 EJ y
mL3
k11
m
0 ,85 104
7 1/с
50
Н/м
f
1,16 Гц
2

4.

Рассмотрим изгибные колебания свободно опертого стержня с массой М по
середине
EJy
М
L
L = 2 м, сечение прямоугольное шириной b = 5 см и высотой h = 3 см,
Е = 200 000 Мпа, М = 50 кг
Уравнение для определения собственных частот колебаний
k 2m 0
1 2m f 0
1
mf
Определим единичную податливость методом сил

5.

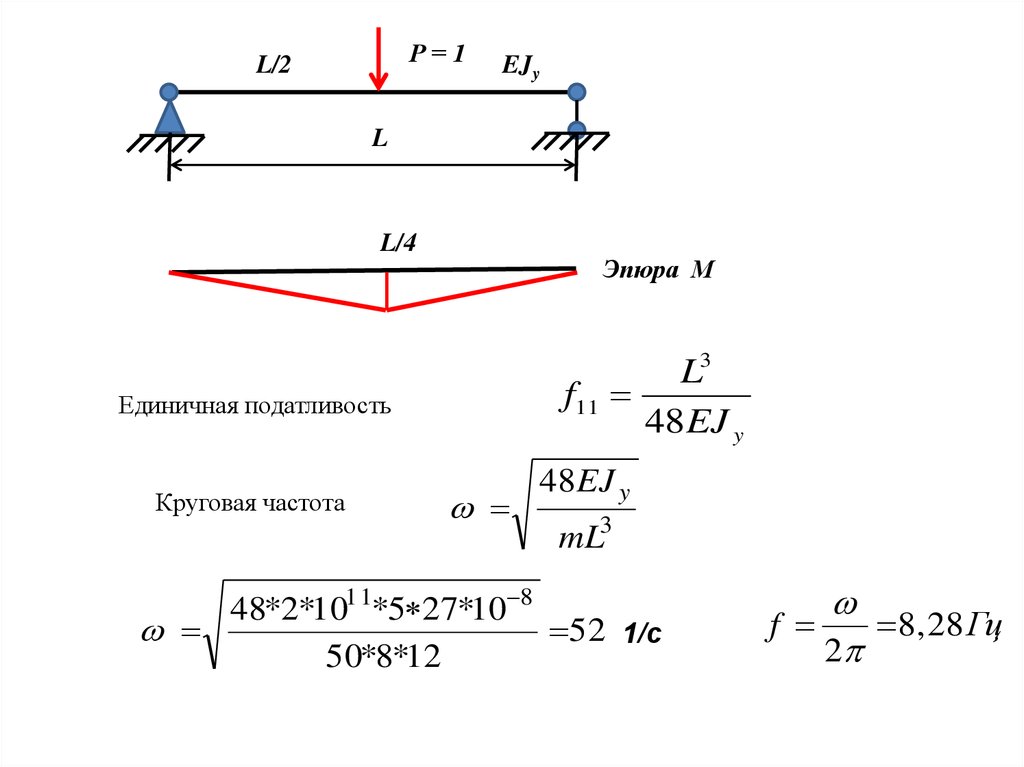
Р=1
L/2
EJy
L
L/4
Эпюра М
L3
f11
48 EJ y
Единичная податливость
Круговая частота
48 EJ y
mL3
48*2*1011*5 27*10 8
52 1/с
50*8*12
f
8, 28 Гц
2

6.

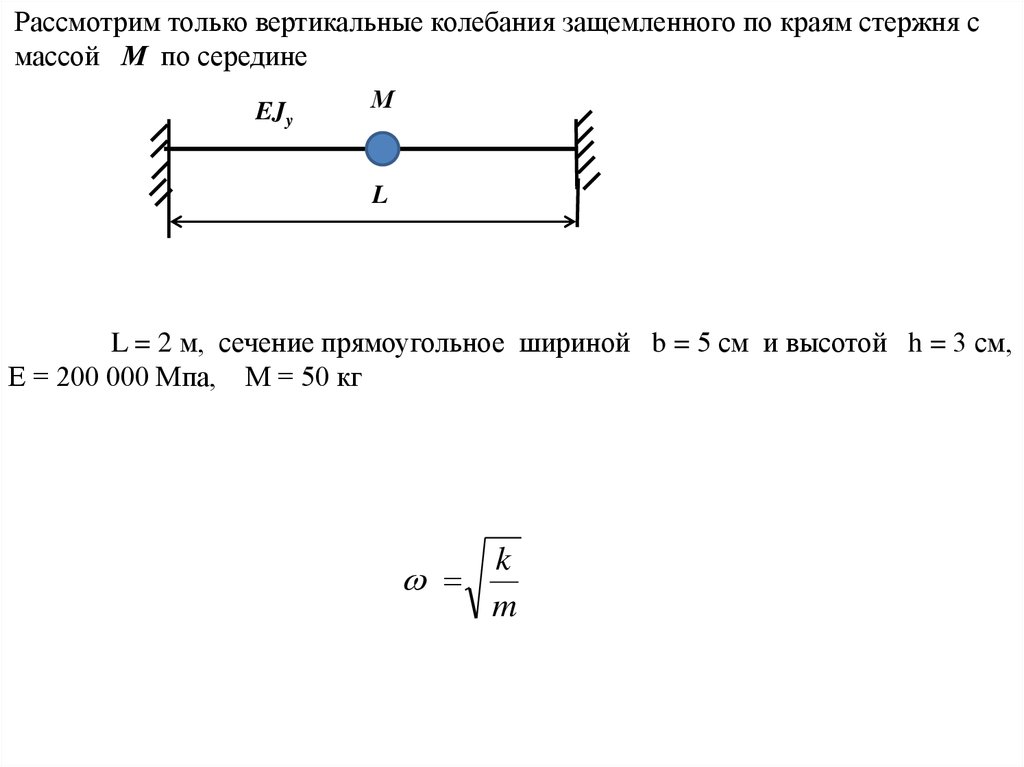
Рассмотрим только вертикальные колебания защемленного по краям стержня с
массой М по середине
EJy
М
L
L = 2 м, сечение прямоугольное шириной b = 5 см и высотой h = 3 см,
Е = 200 000 Мпа, М = 50 кг
k
m

7.

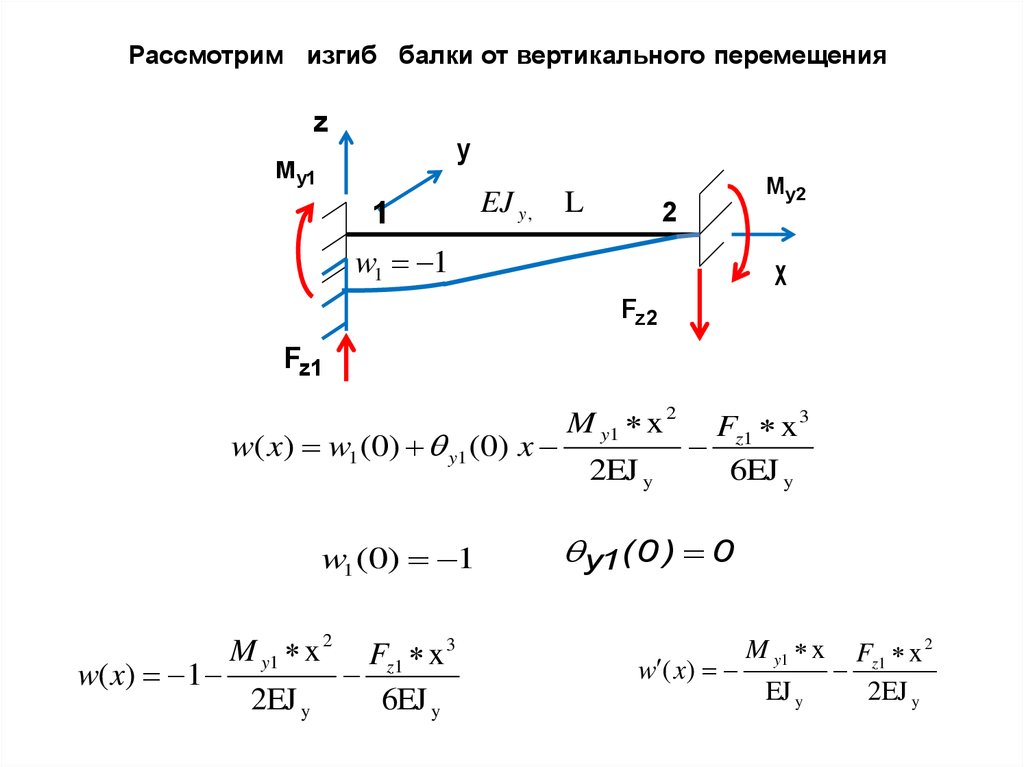
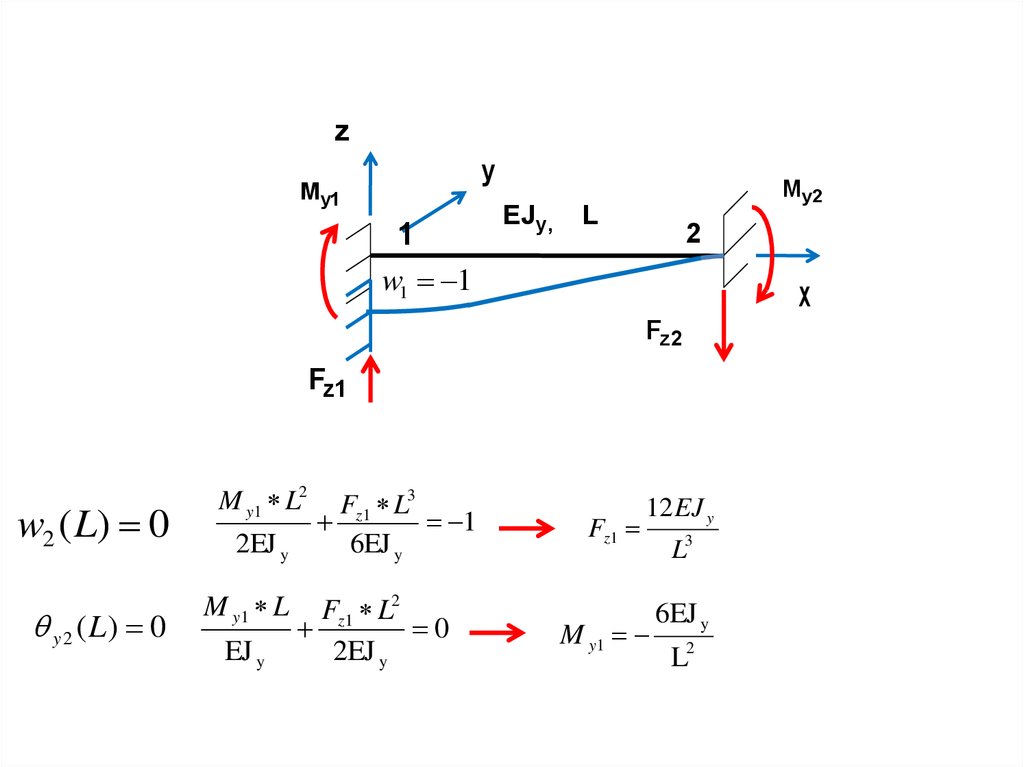
Рассмотрим изгиб балки от вертикального перемещения
z
y
My1
1
EJ y ,
L
M y2
2
w1 1
x
Fz 2
Fz1
w( x) w1 (0) y1 (0) x
w1 (0) 1
w( x) 1
M y1 x 2
2EJ y
Fz1 x 3
6EJ y
M y1 x 2
2EJ y
Fz1 x 3
6EJ y
y1( 0 ) 0
w ( x)
M y1 x
EJ y
Fz1 x 2
2EJ y

8.

z
y
My1
1
w1 1
EJy,
M y2
L
2
x
Fz 2
Fz1
w2 ( L) 0
y 2 ( L) 0
M y1 L2
2EJ y
M y1 L
EJ y
Fz1 L3
1
6EJ y
Fz1 L2
0
2EJ y
Fz1
12 EJ y
M y1
L3
6EJ y
L2

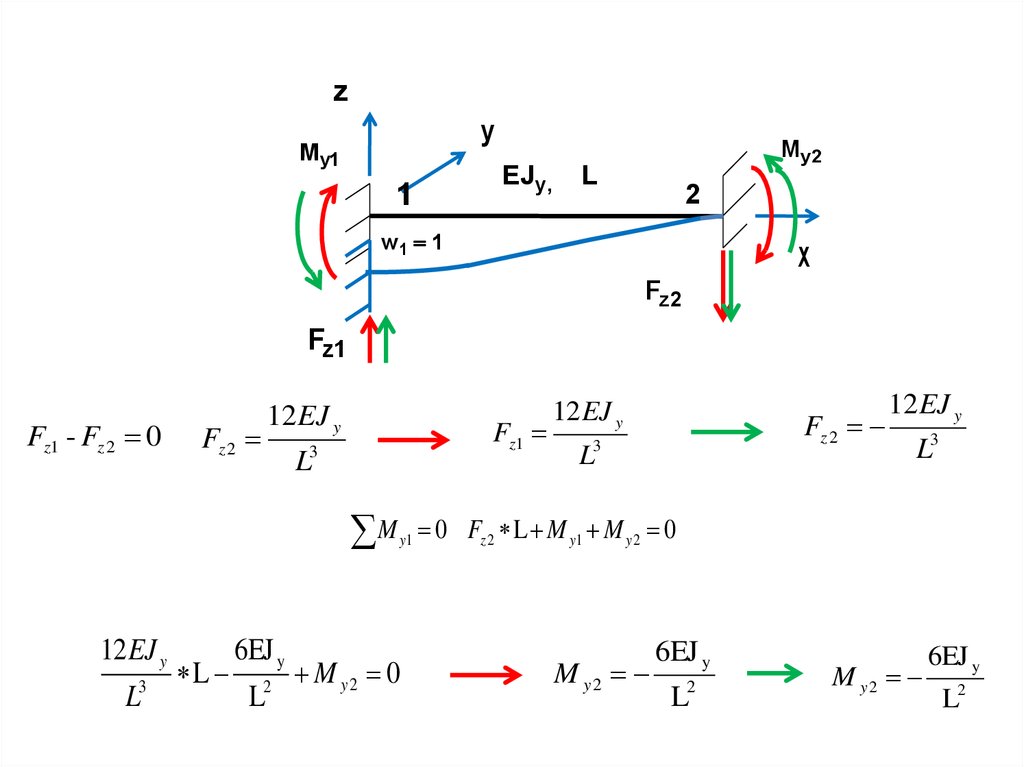
9.

z
y
My1
EJy,
1
M y2
L
2
w1 1
x
Fz 2
Fz1
Fz1 - Fz 2 0
12 EJ y
Fz 2
Fz1
3
L
M
12 EJ y
3
L
L
6EJ y
2
L
y1
M y2 0
12 EJ y
Fz 2
3
L
12 EJ y
L3
0 Fz 2 L M y1 M y 2 0
M y2
6EJ y
L2
M y2
6EJ y
L2

10.

EJy
М
L
L = 2 м, сечение прямоугольное шириной b = 5 см и высотой h = 3 см,
Е = 200 000 Мпа, М = 50 кг
Уравнение для определения собственных частот колебаний
k 2m 0
Fz1
12 EJ y
3
L
k z11
2 *12 EJ y
L3 / 8
2*12 EJ y
192EJ y
k
3
m
m*L / 8
m*L3
2*12*2*1011*5*27*10 8 *8
104
50*8*12
1/с
f
16, 6 Гц
2

11.

Рассмотрим только вертикальные колебания статически неопределимой балки с
массой М по середине
EJy
М
L
L = 2 м, сечение прямоугольное шириной b = 5 см и высотой h = 3 см,
Е = 200 000 Мпа, М = 50 кг
1
mf
Единичную податливость методом сил
768EJ y
3
m7 L
7 L3
f11
768 EJ y
768*2*1011*5*27*10 8
78
50*7*8*12
1/с
f 12, 6 Гц

12.

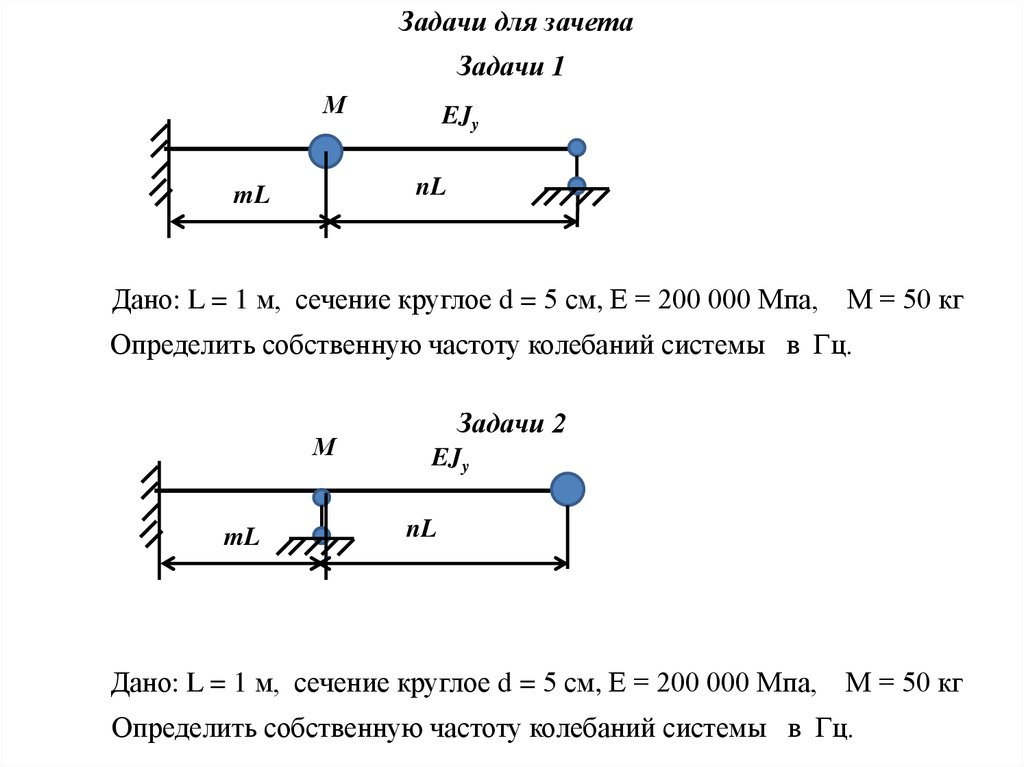
Задачи для зачета
Задачи 1
М
EJy
nL
mL
Дано: L = 1 м, сечение круглое d = 5 см, Е = 200 000 Мпа, М = 50 кг
Определить собственную частоту колебаний системы в Гц.
М
mL
Задачи 2
EJy
nL
Дано: L = 1 м, сечение круглое d = 5 см, Е = 200 000 Мпа,
М = 50 кг
Определить собственную частоту колебаний системы в Гц.

13.

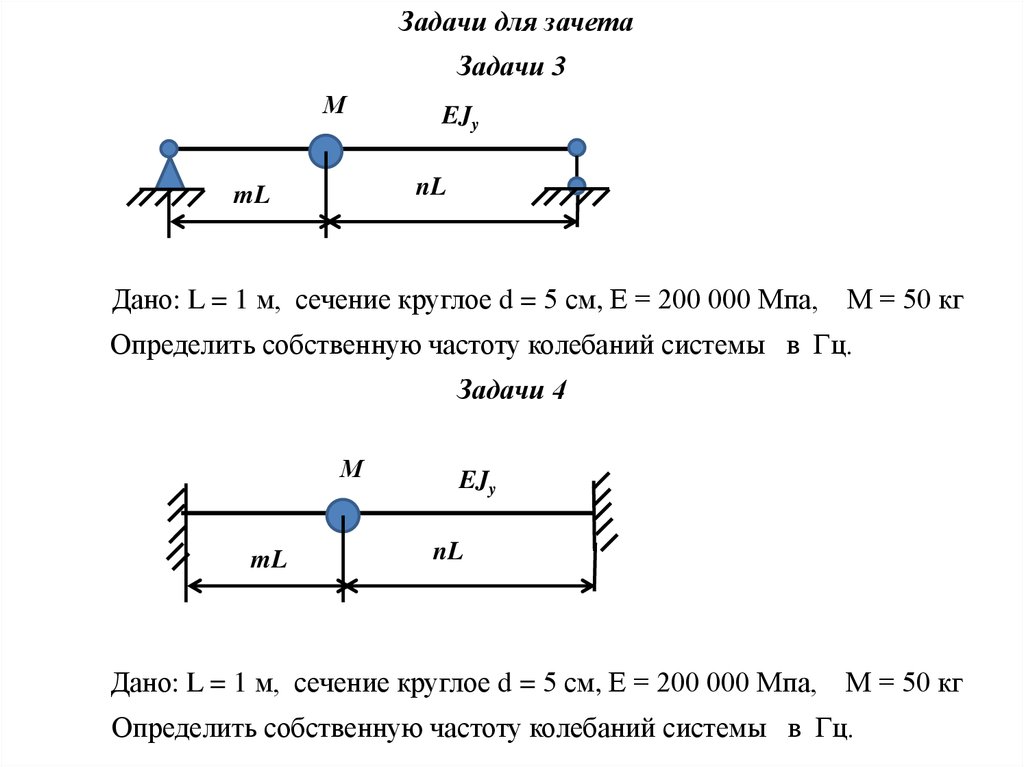
Задачи для зачета
Задачи 3
М
EJy
nL
mL
Дано: L = 1 м, сечение круглое d = 5 см, Е = 200 000 Мпа, М = 50 кг
Определить собственную частоту колебаний системы в Гц.
Задачи 4
М
mL
EJy
nL
Дано: L = 1 м, сечение круглое d = 5 см, Е = 200 000 Мпа,
М = 50 кг
Определить собственную частоту колебаний системы в Гц.