Свободные колебания системы с несколькими степенями свободы

1. Лекция 9-10 Свободные колебания системы с несколькими степенями свободы

Содержание
1.Вековое уравнение.
2.Спектр собственных частот и формы
собственных колебаний.
3.Ортогональность
собственных
форм.

2. Свободные колебания системы с несколькими степенями свободы.

ryi mi yi// 0,
yi ( yi )o Sin ( t o ),
i 1,2,...n
I i mi yi//
(уi)o – представляет собой амплитудное значение перемещения i
– ой массы , а ω – частоту свободных колебаний масс.
I1 m1 y1o 2 Sin ( t o ),
I 2 m 2 y2 o 2 Sin ( t o ),
.........................................,
I n mn yno 2 Sin ( t o )
i 1,2,3,...n

3. Перемещения масс. Интегралы Мора при изгибе

….
Перемещения масс. Интегралы Мора при изгибе
y1 I1 11 I 2 12 ..... I n 1n ,
y2 I1 21 I 2 22 ..... I n 2 n ,
.............................................,
yn I1 n1 I 2 n 2 ..... I n nn
M 1 М 10 dx
11
;
EI
M n М10dx
n1
;
EI
M 1 М 20 dx
12
;
EI
M n М dx
n2
;
EI
0
2
1n
M 1 М n0 dx
;
EI
M n М n0dx
nn
;
EI

4. Вековое уравнение

(m1 11 2 1) y1o m2 12 2 y2o ... mn 1n 2 yno 0,
2
2
2
m
y
m
(
1
)
y
...
m
yno 0,
2o
n 2n
• 1 21 1o 2 22
................................................................................,
m1 n1 2 y1o m2 n 2 2 y2o ... (mn nn 2 1) yno 0,
(m1 11 )
m 21
m 2 12
...
m n 1n
(m 2 22 ) ...
mn 2n
...
...
m1 n1
m 2 n 2
...
...
... (m n nn )
0
1
2
(1)

5. Вековое уравнение для системы с двумя степенями свободы

1,2
(m1 11 m2 22 ) (m1 11 m2 22 ) 2 4m1m2 ( 11 22 122 )
2m1m2 ( 11 22 )
2
12
Движение к-ой массы
n
yk yki Sin ( i t ),
1
k 1,2,...n

6. Собственные формы колебаний

y1i
1i
1,
y1i
y2i
2i
,
y1i
y3 i
yni
3i , ... ni
,
y1i
y1i
(2)
(m1 11 i 1) m2 12 i 2i ... mn 1n i ni 0,
2
2
2
m1 21 i (m 2 22 i 1) 2i ... m n 2 n i ni 0,
2
2
2
................................................................................,
m1 n1 i m 2 n 2 i 2i ... (m n nn i 1) ni 0,
2
2
2
Полное перемещение к-ой массы
n
yk (t ) ki y1i Sin ( i t ),
1
k 1,2,...n
(3)

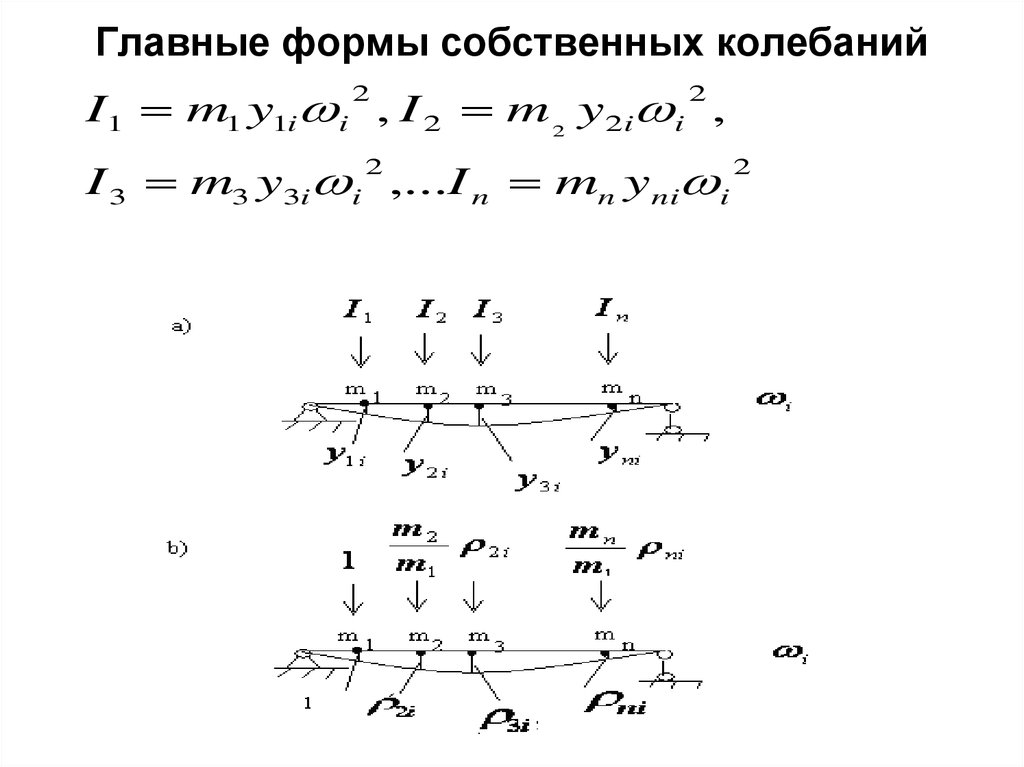
7. Главные формы собственных колебаний

I1 m1 y1i i , I 2 m 2 y2i i ,
2
2
I 3 m3 y3i i ,...I n mn yni i
2
2

8. Ортогональность главных форм колебаний

n
Aim mk i2 y ki Sin i t y km Sin m t ,
k 1
n
Amn mk m2 y km Sin m t y ki Sin i t ,
k 1
n
( ) mk y ki y km 0,
2
i
2
m
n
m
k 1
k
k 1
y ki y km 0
i m ,

9. Свойство ортогональности для системы с двумя степенями свободы

m1 y12 y11 m2 y21 y22 0

10. Разложение нагрузки по нормальным составляющим

P1 C1m1 y11 C2 m1 y12 ,
P2 C1m2 y21 C2 m2 y22
2
C1
Py
i
i1
1
2
,
m
i
yi21
1
2
C2
Py
i
i2
1
2
m
i
yi22
1
n
Pk (t ) Ci i2 mk yki ,
i 1
k 1,2,....n

11. Нормальные составляющие внешней нагрузки