Похожие презентации:
Компьютерное и математическое моделирование. Тема 7. Математическая модель деформирования оболочки
1.
Санкт-Петербургский государственныйархитектурно-строительный университет
0
кафедра Информационных технологий
b
a
z
y
x
R1
Компьютерное и математическое моделирование
Тема 7
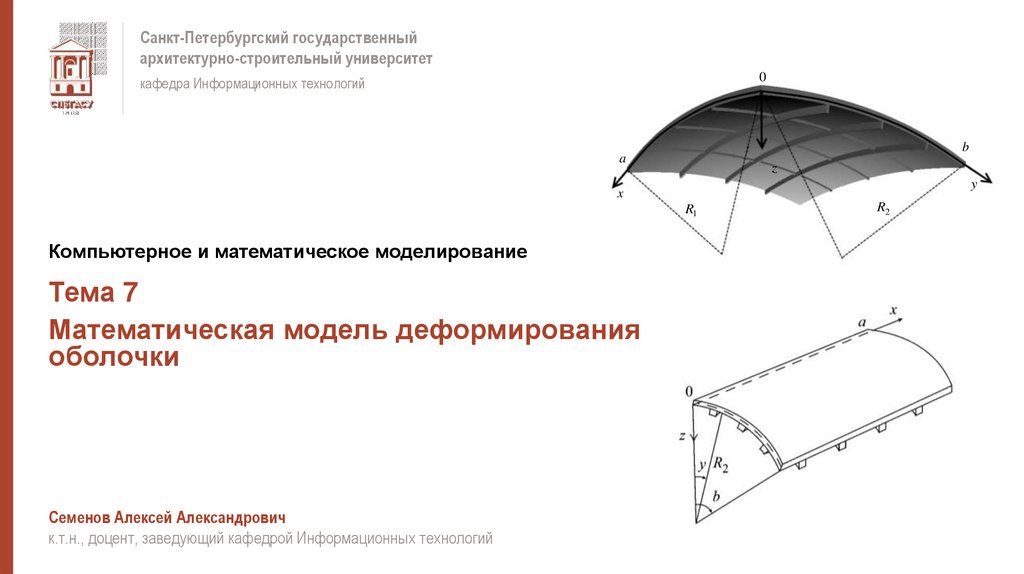
Математическая модель деформирования
оболочки
Семенов Алексей Александрович
к.т.н., доцент, заведующий кафедрой Информационных технологий
R2
2.
Гипотеза прямой нормали.Теория оболочек Кирхгофа – Лява (CSDT)
2
Для тонкостенных конструкций (балка, плита, оболочка) вводятся гипотезы,
позволяющие для характеристик НДС (перемещения, деформации, напряжения)
принять линейный закон их изменений по толщине конструкции (вдоль оси Oz).
Тем самым, например, для оболочки и плиты достаточно знать НДС срединной
поверхности (срединной плоскости) конструкций, то есть рассматривать уже не
трёхмерную задачу, а двухмерную.
Для плиты рассматривают двумерную задачу (перемещения, деформации,
напряжения рассматриваются изменяющимися только вдоль осей Ox и Oy).
Основная гипотеза механики – это гипотеза прямой нормали.
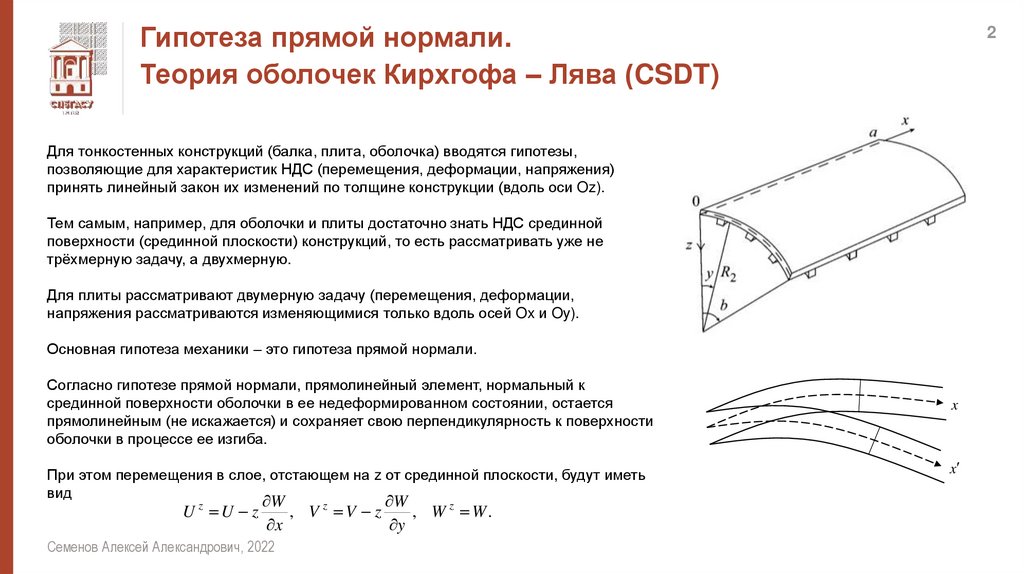
Согласно гипотезе прямой нормали, прямолинейный элемент, нормальный к
срединной поверхности оболочки в ее недеформированном состоянии, остается
прямолинейным (не искажается) и сохраняет свою перпендикулярность к поверхности
оболочки в процессе ее изгиба.
При этом перемещения в слое, отстающем на z от срединной плоскости, будут иметь
вид
U z U z
W
W
, V z V z
, W z W.
x
y
Семенов Алексей Александрович, 2022
x
x
3.
Основные допущения1.
Материал, из которого изготовлена строительная конструкция, представляет собой однородную сплошную среду.
Следовательно, все характеристики НДС в конструкции (перемещения, деформации, напряжения) являются
непрерывными функциями координат, и не только непрерывными, но и дифференцируемыми. Таким образом,
далее можно использовать математический анализ (дифференциальное, интегральное, вариационное
исчисление и др.).
2.
Если специально не обговаривается, то считается, что материал конструкции работает в упругой зоне, то есть
после снятия нагрузки он восстанавливает свои первоначальные размеры.
3.
Обычно принимается, что материал конструкции изотропный, то есть свойства материала не зависит от его
исходной угловой ориентации.
4.
Для тонкостенных конструкций (балка, плита, оболочка) считается что напряжение z мало по сравнению с
другими напряжениями и им можно пренебречь.
5.
Для тонкостенных конструкций можно использовать гипотезу прямой нормали (гипотезу плоских сечений).
6.
Если рассматривается геометрически линейный вариант деформирования конструкции, то прогиб не должен
превышать значения толщины конструкции и геометрические соотношения будут линейными.
Могут быть и другие допущения, которые оговариваются специально.
Семенов Алексей Александрович, 2022
3
4.
Параметры Ляме4
x
a
x
a
M
V
a1
0
z
y
y
b
R
R
Семенов Алексей Александрович, 2022
0
U
b
W
R
x
y
5.
Геометрические соотношенияq ( x, y )
y
b
x
R2
a
R1
z
5
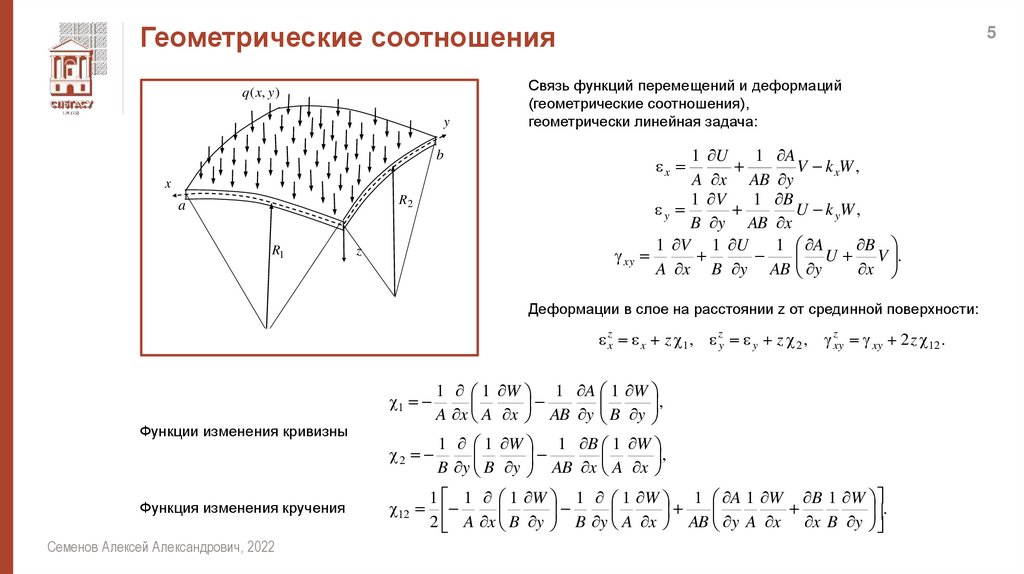
Связь функций перемещений и деформаций
(геометрические соотношения),
геометрически линейная задача:
1 U
1 A
V k xW ,
A x AB y
1 V
1 B
y
U k yW ,
B y AB x
1 V 1 U
1 A
B
xy
U V .
A x B y AB y
x
x
Деформации в слое на расстоянии z от срединной поверхности:
zx x z 1 , zy y z 2 , zxy xy 2 z 12 .
1
1 1 W 1 A 1 W
,
A x A x AB y B y
2
1 1 W 1 B 1 W
,
B y B y AB x A x
Функции изменения кривизны
Функция изменения кручения
Семенов Алексей Александрович, 2022
1 1 1 W 1 1 W 1 A 1 W B 1 W
12
.
2 A x B y B y A x AB y A x x B y
6.
Физические соотношения(линейно-упругая задача)
6
Изотропный материал:
q ( x, y )
y
x
b
E
E
E
z
z
z
z
,
,
zxy .
x
y
y
y
x
xy
2
2
2 1
1
1
Ортотропный материал:
x
R2
a
R1
z
Семенов Алексей Александрович, 2022
x
E1
E2
zx 21 zy , y
zy 12 zx , xy G12 zxy .
1 12 21
1 12 21
7.
Усилия и моментыУсилия и моменты получаются интегрированием компонент напряжений по толщине оболочки:
Изотропный случай:
Ортотропный случай:
E
E
h
,
N
h y x ,
x
y
y
1 2
1 2
E h3
E h3
1 2 , M y
2 1 ,
Mx
1 2 12
1 2 12
E
E h3
12 ,
N xy N yx
h xy , M xy M yx
2 1
1 12
Nx
E1
E2
h x 21 y , N y
h y 12 x ,
1 12 21
1 12 21
h3
h3
E1
E2
1 21 2 , M y
2 12 1 ,
Mx
1 12 21 12
1 12 21 12
h3
N xy N yx G12 h xy , M xy M yx 2G12 12 ,
12
Nx
Семенов Алексей Александрович, 2022
7
8.
Функционал полной потенциальной энергиидеформации (линейно-упругая задача)
Es E p
1ab
1
Es N x x N y y N xy N yx xy M x 1 M y 2 M xy M yx 12 2 PxU PyV qW ABdxdy .
200
2
Семенов Алексей Александрович, 2022
8
9.
Санкт-Петербургский государственныйархитектурно-строительный университет
кафедра Информационных технологий
Автор:
Семенов Алексей Александрович
pmi@spbgasu.ru






 Математика
Математика Механика
Механика








