Математические модели линейных цифровых систем

1. Введение в задачи исследования и проектирования цифровых систем

Санкт-Петербургский государственный университет
Факультет прикладной математики - процессов управления
Веремей Е.И.
Введение в задачи
исследования и проектирования
цифровых систем
Лекции 2 ─ 5
Раздел 1. Математические модели
линейных цифровых систем

2.

Математические модели DLTI систем
1
1. Преобразование дискретных сигналов линейными
системами
{u[n]}
Hn{∙}
y[n]
n N
1
u[n], y[n] R
1
Система, преобразующая дискретный сигнал u[n]
1. y[n] 2(u[n])
2
2. y[n] 2 (u[n]) u[n 1]
2
3. y[n] 2u[n] u[n 1] 5 y[n 2]

3.

Математические модели DLTI систем
2
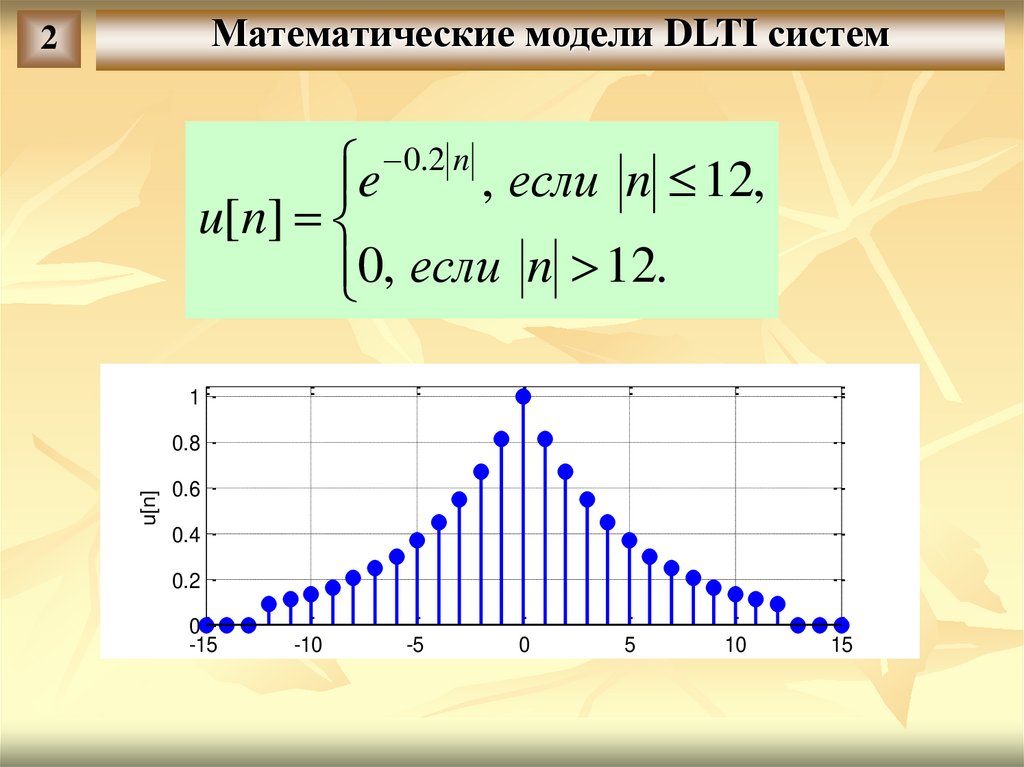
e 0.2 n , если n 12,
u[n]
0, если n 12.
1
u[n]
0.8
0.6
0.4
0.2
0
-15
-10
-5
0
n
5
10
15

4.

Математические модели DLTI систем
3
Единичный импульс
1
1 если n 0,
[n]
0, если n 0
x[n]
0.8
0.6
0.4
0.2
0
-10
-5
0
n
5
10
1 если n k ,
[n k ]
0, если n k
1
x[n]
0.8
0.6
0.4
0.2
0
-10
-5
0
n
5
u[n]
10
u[k ] [n k ]
k

5.

4
Математические модели DLTI систем
{ [n k ]}
hk [n] H n [n k ]
h[n] H n [n]
Hn{∙}
hk [n]
y[n]
u[k ] h [n].
k
k
y[n]
u[k ] h[n k ].
k
y[n] u[n] h[n]

6.

Математические модели DLTI систем
5
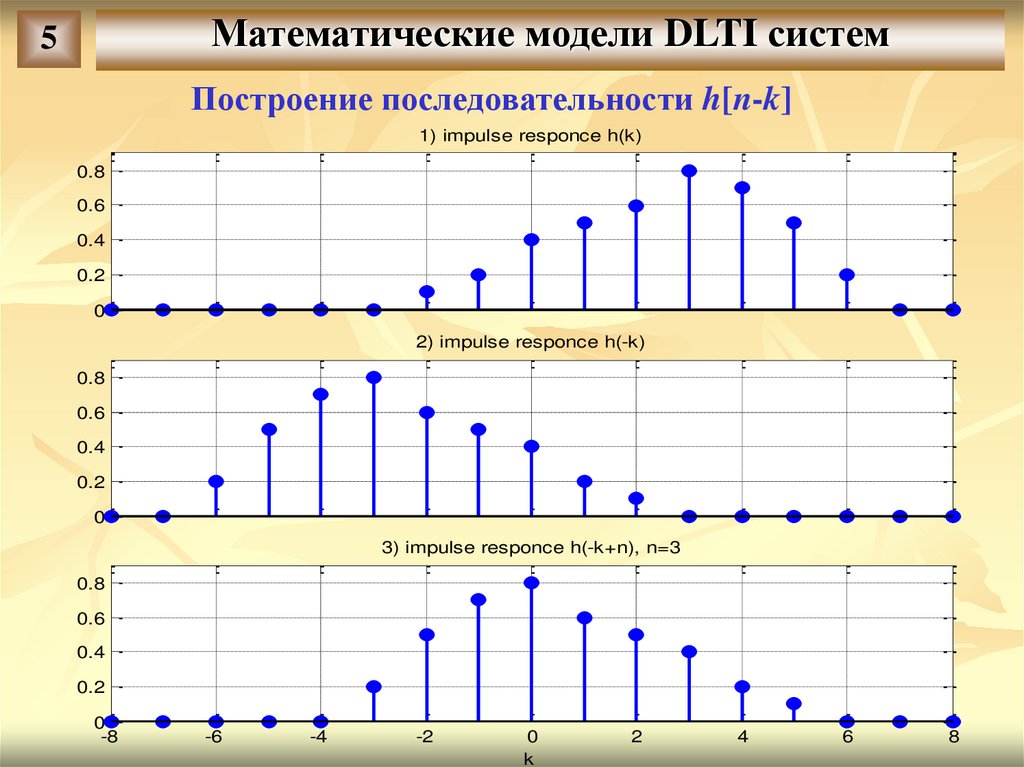
Построение последовательности h[n-k]
1) impulse responce h(k)
0.8
0.6
0.4
0.2
0
2) impulse responce h(-k)
0.8
0.6
0.4
0.2
0
3) impulse responce h(-k+n), n=3
0.8
0.6
0.4
0.2
0
-8
-6
-4
-2
0
k
2
4
6
8

7.

Математические модели DLTI систем
6
2. Математические модели DLTI систем в виде
разностных уравнений
y { y[n]}
y { y[n]}
y[n] y[n] y[n 1], n N
1
Первая обратная конечная разность
F n, y[n], y[n], y[n], ..., y[n] 0
2
N

8.

Математические модели DLTI систем
7
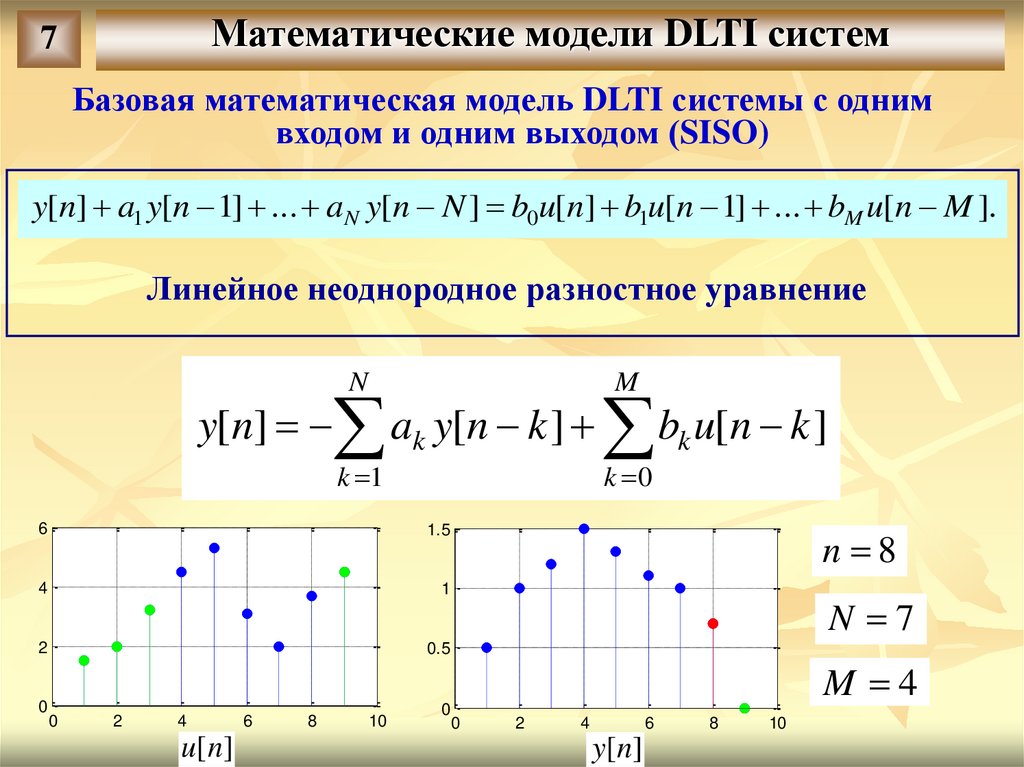
Базовая математическая модель DLTI системы с одним
входом и одним выходом (SISO)
y[n] a1 y[n 1] ... a N y[n N ] b0u[n] b1u[n 1] ... bM u[n M ].
Линейное неоднородное разностное уравнение
y[n]
N
M
a y[n k ] b u[n k ]
k
k
k 1
k 0
6
1.5
4
1
2
0.5
0
0
2
4
u[n ]
6
8
10
0
n 8
N 7
M 4
0
2
4
6
y[n]
8
10

9.

8
Математические модели DLTI систем
ТИПЫ SISO DLTI МОДЕЛЕЙ
y[n] a1 y[n 1] ... a N y[n N ] b0u[n] b1u[n 1] ... bM u[n M ].
Модель авторегрессии со скользящим средним (АРСС)
Autoregressive moving average (ARMA) model
y[n] a1 y[n 1] ... a N y[n N ] b0u[n].
Модель авторегрессии (АР)
Autoregressive (AR) model
y[n] b0u[n] b1u[n 1] ... bM u[n M ].
Модель скользящего среднего (СС)
Moving average (MA) model

10.

9
Математические модели DLTI систем
ЦИФРОВЫЕ ФИЛЬТРЫ
y[n] a1 y[n 1] ... a N y[n N ] b0u[n] b1u[n 1] ... bM u[n M ].
АРСС (ARMA)
– рекурсивные цифровые фильтры
АР (AR)
CC (MA)
– нерекурсивные цифровые фильтры
{ [n]}
H n { }
{h[n]} {b0 , b1 ,..., bM }
h[n]
КИХ (FIR) фильтры

11.

Математические модели DLTI систем
10
Разностные уравнения DLTI систем в пространстве
состояний
y[n] a1 y[n 1] ... a N y[n N ] b0u[n].
Модель АР
(авторегрессия)
x[n 1] Ax[n] bu[n],
y[n] cx[n] du[n].
0
0
A ...
0
a
N
1
0
0
1
...
...
0
0
a N 1 a N 2
c a N
... 0
... 0
... ...
... 1
... a1
a N 1
0
0
b ...
0
b
0
aN 2
... a1
d b0

12.

11
Математические модели DLTI систем
3. Z – пробразование (Преобразование Лорана)
F F (z)
f { f [n]}
F ( z ) Z { f [n]}
f [ n] z
Прямое
преобразование
n
n
1 если n 0,
[n]
0, если n 0.
1 если n 0,
ue [ n]
0, если n 0,
f [n] A ue [n]
n
F ( z ) Z{ [n]}
[n]z n 1 z 0 1
n
F ( z ) Z{ue [n]}
[n]z n
n
F ( z)
A( z 1 ) n
n 0
A
Az
1 z 1 z
( z 1 ) n

13.

Математические модели DLTI систем
12
№
f [n]
F (z )
1.
[n]
1
2.
u e [n ]
z
z 1
3.
A nue [n]
Az
z
f1[n], f 2 [n]
F1 ( z ), F2 ( z )
4.
1F1 ( z ) 2 F2 ( z )
1 f1[n] 2 f 2 [n]
5.
f [n m]
6.
f1[n] f 2 [n]
z m F (z )
F1 ( z ) F2 ( z )

14.

13
Математические модели DLTI систем
Одностороннее z-преобразование
F F (z)
f { f [n]}
F ( z ) Z 0{ f [n]}
f [ n] z
n
n 0
f m { f [n m]}
f [n]u [n]z
n
e
n
m 0
Fm ( z ) Z 0 { f m [n]}
1
m
p
Fm ( z ) z
F ( z)
f [ p]z
p
m

15.

14
Математические модели DLTI систем
Обратное z-преобразование
F F (z)
f { f [n]} Z
1
F ( z)
n
z
f [n] F ( z ) dz
z
n
z
z
f [n] F ( z ) dz
Res F ( z ) , zi
z
z
i
1
n
k

16.

Математические модели DLTI систем
15
Обратное z-преобр. для дробно-рациональных функций
F F (z)
f { f [n]} Z
1
F ( z)
zB ( z )
A( z ) ans ( z 1 )( z 2 )...( z ns )
F ( z)
A( z )
F ( z)
ns
i 1
B ( i )
z
i A' ( i ) z i
f i { f i [n]}
f i [ n]
f Z 1 F ( z )
n
f,
i
i 1
Ai inue [n]
B ( i )
Ai
i A' ( i )

17.

16
Математические модели DLTI систем
Решение разностных уравнений в изображениях
y[n] a1 y[n 1] ... a N y[n N ] b0u[n] b1u[n 1] ... bM u[n M ].
b0 b1 z 1 b2 z 2 ... bM z M
Y ( z)
U ( z)
1
2
N
1 a1 z a2 z ... a N z
U ( z ) Z u[n]
Y ( z ) Z y[n]
x[n 1] Ax[n] Bu[n]
X( z ) Z x[n] U( z ) Z u[n]
X( z ) (Ez A) 1 BU( z )

18.

17
Математические модели DLTI систем
4. Модели DLTI систем в изображениеях по Лорану
x[n 1] Ax[n] Bu[n],
u[n] E
y[n] Cx[n] Du[n].
ms
y[n] E k s
x[n] E
Y( z ) C(Ez A) B D U( z )
1
ПЕРЕДАТОЧНАЯ МАТРИЦА
1
H( z) C(Ez A) B D,
y H( z)u,
H( z ) : A, B, C, D
ns

19.

18
Математические модели DLTI систем
Передаточные функции цифровых фильтров
y[n] a1 y[n 1] ... a N y[n N ] b0u[n] b1u[n 1] ... bM u[n M ].
b0 b1 z 1 b2 z 2 ... bM z M
Y ( z)
U ( z)
1
2
N
1 a1 z a2 z ... a N z
y H ( z)u
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ ФИЛЬТРА
1
2
M
Y ( z ) b0 b1 z b2 z ... bM z
H ( z)
U ( z ) 1 a1 z 1 a2 z 2 ... a N z N