Признаки равенства углов

1. Признаки равенства углов

Образовательный комплекс "Школа №29 г. Йошкар-Олы" им. Героя Российской
Федерации Д.Э. Шаймарданова
Признаки равенства углов
Преподаватель Мусина Н.А.
Работа ученика 7 "г" класса
Павлова Матвея
2023 г.

2.

Треугольник
В
В
Треугольник - простейшая
плоская фигура, которая
состоит из трёх точек, не
лежащих на одной прямой, и
трёх отрезков, соединяющих
эти точки.
С
А
С

3.

Свойства равных треугольников
У равных треугольников все соответствующие
элементы равны (стороны, углы, высоты,
медианы, биссектрисы)
У равных треугольников против равных сторон
лежат равные углы, а против равных углов равные
стороны.
Сумма углов треугольника равна 180°.

4.

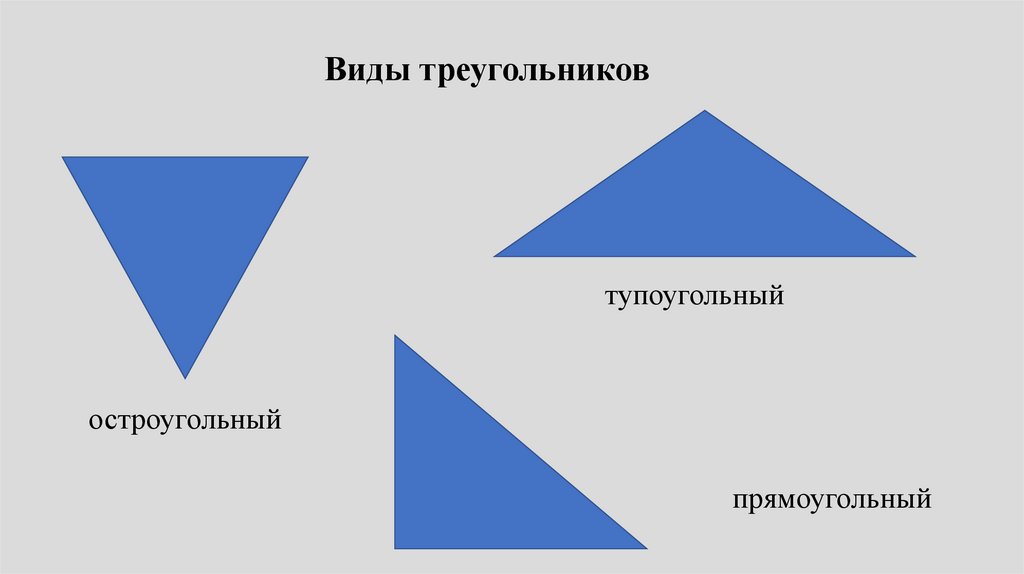
Виды треугольников
тупоугольный
остроугольный
прямоугольный

5.

А также разносторонний, равносторонний и
равнобедренный треугольник
B
K
M
K
N
разносторонний
E
F
равносторонний
A
C
равнобедренный

6.

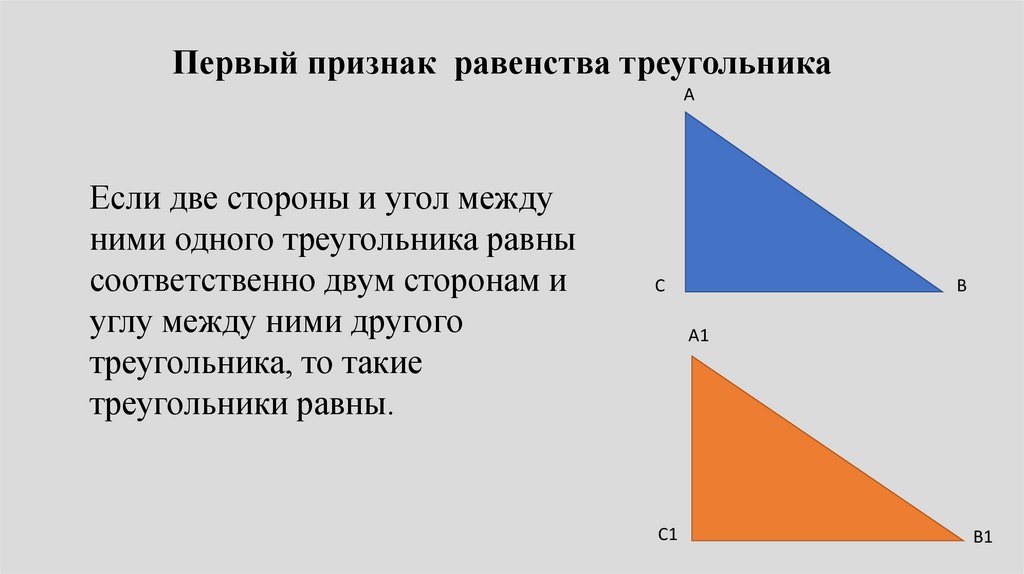
Первый признак равенства треугольника
А
Если две стороны и угол между
ними одного треугольника равны
соответственно двум сторонам и
углу между ними другого
треугольника, то такие
треугольники равны.
С
В
А1
С1
В1

7.

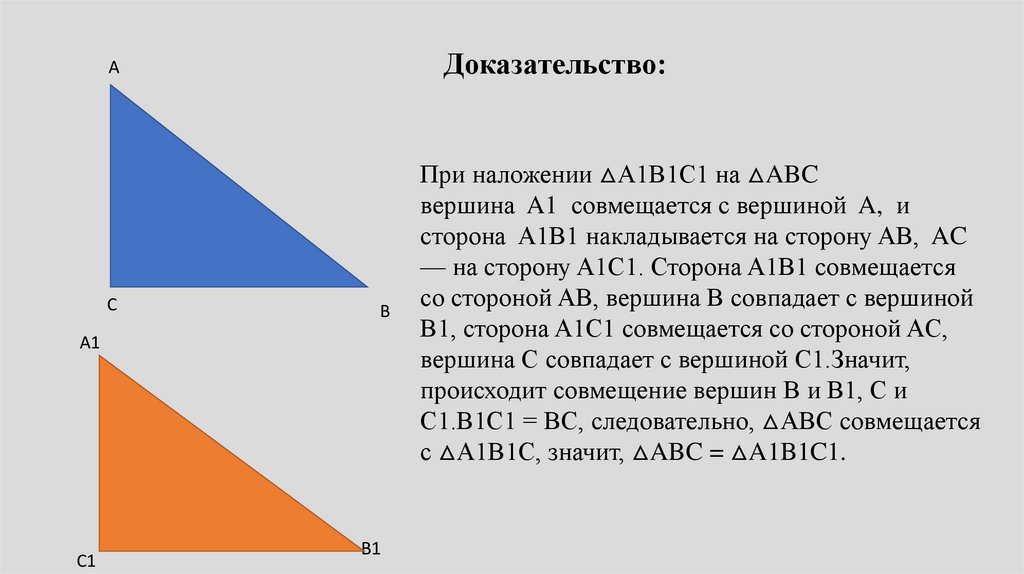
Доказательство:
А
С
В
А1
С1
В1
При наложении △A1B1C1 на △ABC
вершина A1 совмещается с вершиной A, и
сторона A1B1 накладывается на сторону AB, AC
— на сторону A1C1. Сторона A1B1 совмещается
со стороной AB, вершина B совпадает с вершиной
B1, сторона A1С1 совмещается со стороной AС,
вершина C совпадает с вершиной C1.Значит,
происходит совмещение вершин В и В1, С и
С1.B1C1 = BC, следовательно, △ABC совмещается
с △A1B1C, значит, △ABC = △A1B1C1.

8.

Второй признак равенства треугольников
Теорема
Если сторона и два прилежащих
к ней угла одного треугольника
соответственно равны стороне
и двум прилежащим к ней
углам другого треугольника, то
такие треугольники равны.
А1
А
С1
С
В
В1

9.

Доказательство
Дано:∆ABC, ∆А1В1С1,
АC = А1C1,
∠А =∠А1
∠C=∠C1
Доказать: ∆АВС = ∆А1В1С1.
Доказательство
Наложим треугольник ∆ABC на ∆А1В1С1, так чтобы вершина A
совместилась с вершиной A1, вершины B и B1лежали по одну сторону от
A1C1.
Так как ∠А =∠А1, ∠C=∠C1, то AB наложится на луч A1B1, BC наложится на
луч B1C1 (по аксиоме откладывания угла).
Вершина B – с вершиной B1 (по аксиоме откладывания отрезка).
Стороны треугольников BС и B1С1, АВ и А1В1совместятся (по аксиоме
откладывания отрезка).
Треугольник ABC и треугольник А1В1С1 полностью совместится →∆АВС =
∆А1В1С1
Теорема доказана.

10.

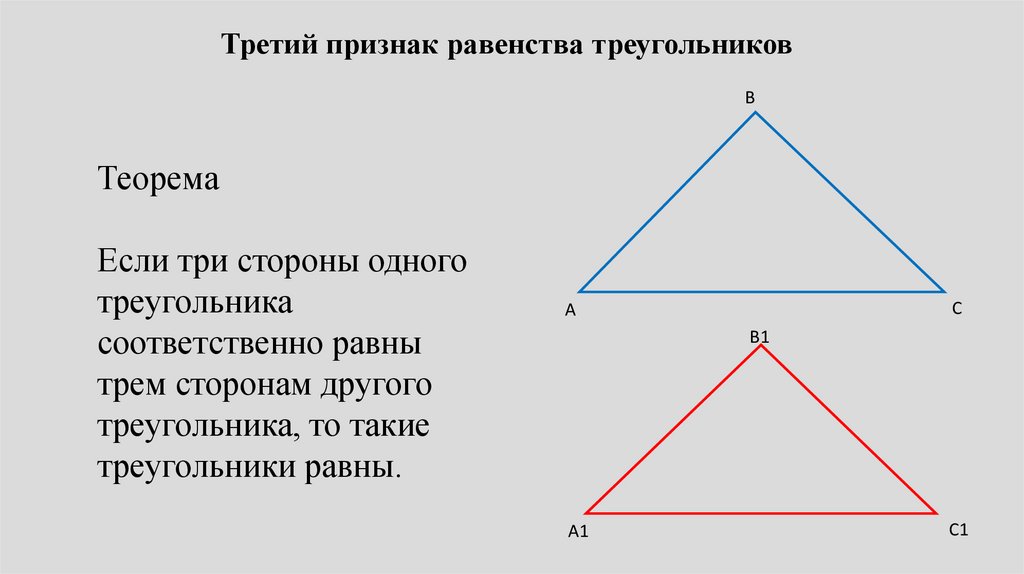
Третий признак равенства треугольников
В
Теорема
Если три стороны одного
треугольника
соответственно равны
трем сторонам другого
треугольника, то такие
треугольники равны.
С
А
В1
А1
С1

11.

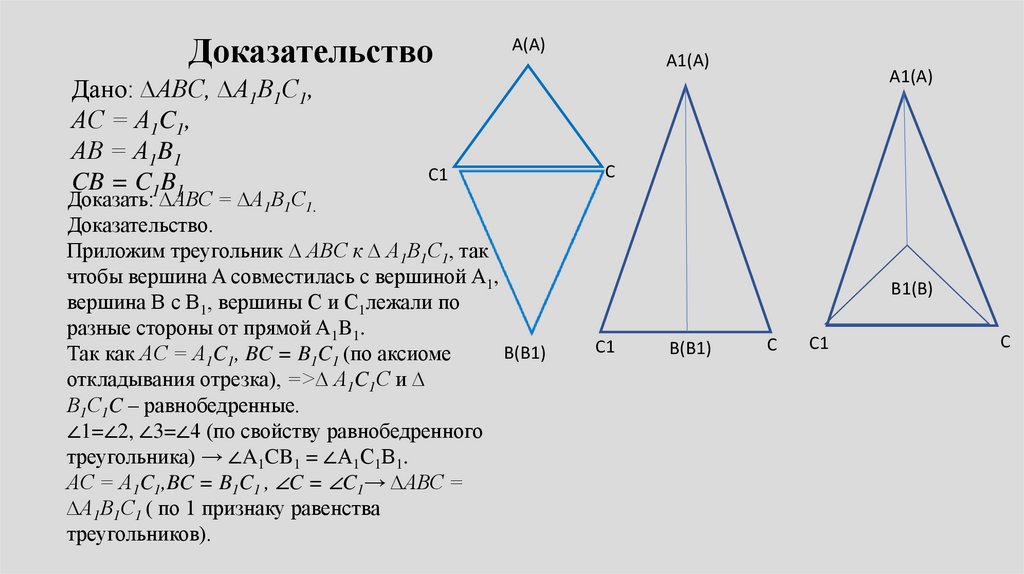
Доказательство
Дано: ∆ABC, ∆А1В1С1,
АC = А1C1,
АB = А1B1
CB = C1B1
А(А)
С1
Доказать: ∆АВС = ∆А1В1С1.
Доказательство.
Приложим треугольник ∆ ABC к ∆ А1В1С1, так
чтобы вершина A совместилась с вершиной A1,
вершина B с B1, вершины C и C1лежали по
разные стороны от прямой A1B1.
В(В1)
Так как АC = А1C1, BC = B1C1 (по аксиоме
откладывания отрезка), =>∆ А1C1С и ∆
В1С1C – равнобедренные.
∠1=∠2, ∠3=∠4 (по свойству равнобедренного
треугольника) → ∠A1CB1 = ∠А1С1В1.
АC = А1C1,BC = B1C1 , ∠C = ∠C1→ ∆АВС =
∆А1В1С1 ( по 1 признаку равенства
треугольников).
А1(А)
А1(А)
С
В1(В)
С1
В(В1)
С
С1
С

12.

Четвертый признак равенства треугольников
Теорема
В
А
О
Н
С
Если две стороны и угол,
лежащий против большей из
них одного треугольника
соответственно равны двум
сторонам и углу, лежащему
против большей из них другого
треугольника, то такие
треугольники равны.

13.

Доказательство:
Рассмотрим △ABC и △FHE, которые наложились друг на друга,
AВ = AH,∠ABO = ∠AHO, ∠BOC = ∠HOC.
Докажем, что △ABC = △FHE.
△ABH — равнобедренный (AB = AH), значит ∠ABO = ∠AHO.
∠BOC = ∠HOC, так как остатки равных углов.
△BHC — равнобедренный(∠BOC = ∠HOC), а так как углы при
боковых сторонах HC и BC равны, значит HC = BC.
Итак, △ABC = △FHE по двум сторонам и углу, лежащему
против большей из сторон.

14.

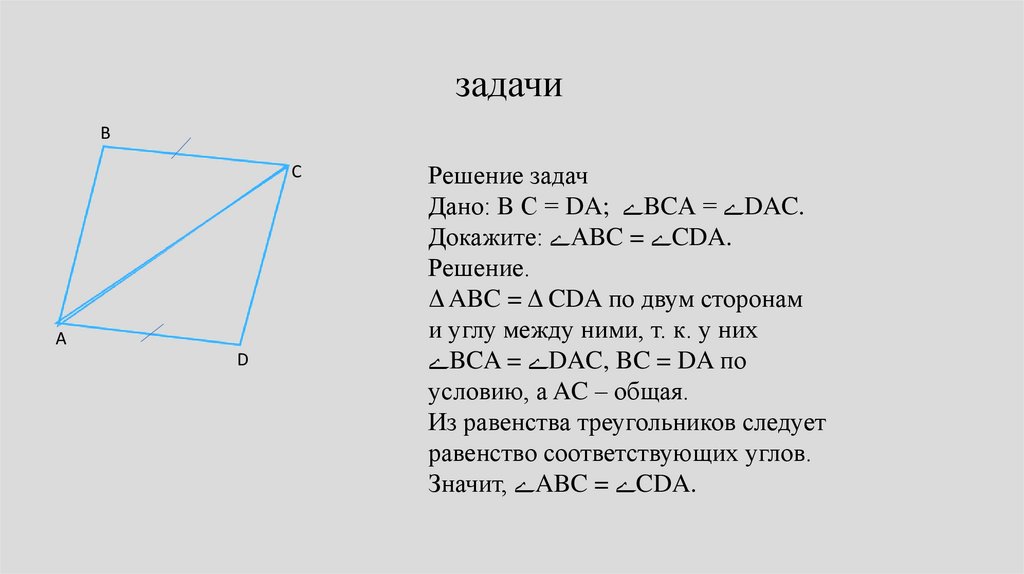
задачи
В
С
А
D
Решение задач
Дано: B С = DA; ‫ے‬BCА = ‫ے‬DAC.
Докажите: ‫ے‬АBC = ‫ے‬CDA.
Решение.
Δ ABC = Δ CDA по двум сторонам
и углу между ними, т. к. у них
‫ے‬BCA = ‫ے‬DAC, BC = DA по
условию, а AC – общая.
Из равенства треугольников следует
равенство соответствующих углов.
Значит, ‫ے‬ABC = ‫ے‬CDA.

15.

B
A
K
Найдите пару равных треугольников и
докажите их равенство.
Решение.
Δ АВК = Δ СВР по двум сторонам и углу
между ними,
т. к. у них АК = СР, ВК = ВР по условию,
‫ے‬АКВ = ‫ے‬СРВ как углы смежные с углами
ВКР и ВРК , равными по условию.
P
C

16.

В работе использован
учебник
Геометрия. 7-9 классы.
Автор Л.С. Атанасян