Похожие презентации:
Энергетическая светимость. Облученность и закон квадрата расстояния
1.
ОблученностьОблученность - отношению элементарного потока излучения dФе ,
упавшего на площадку dA , к её площади
dФe
Ee
dA
Ee ( x, y, z , t )
Вт
м2
Фе
1
Фe
Eе ср Eе ( x, y ) dx dy Eе ср
AA
A
Ee vф
2
0 Emax
2
dФe vф
2
0 Emax
2
dA
А
Облученность
2.
Энергетическая экспозиция, энергетическая светимостьtк
dQ
Энергия излучения, упавшая на
He e
dA
единицу поверхности тела в течение
всего времени облучения, называется
энергетической экспозицией
H e Ee (t )dt
tн
Энергетическая светимость равна отношению
энергетического потока dФe уходящего от
площадки dA к её площади
dФe M ( x, y, z , t )
Фe
Me
M e ср
e
dA
A
В определении Ee –
dФе - поток упавший на площадку dA
H e ( x, y , z )
Дж
м2
Фе
Вт
2
м
dФe
Ee
dA
А
Энергетическая светимость
3.
Облученность и закон квадрата расстоянияdФe
I e ( , )
d
dФе I e ( , )d
dA0 cos( )
d
l2
dA0 cos( )
dФе I e ( , )
l2
dФe
Ee
dA0
I e ( , )
Закон квадрата
Ee (l )
2
расстояния для Ee
l
Закон косинуса
Ee ( ) Ee cos( )
Закон квадрата
расстояния
I е ( , )
Ee (l , )
cos( )
2
l
4.
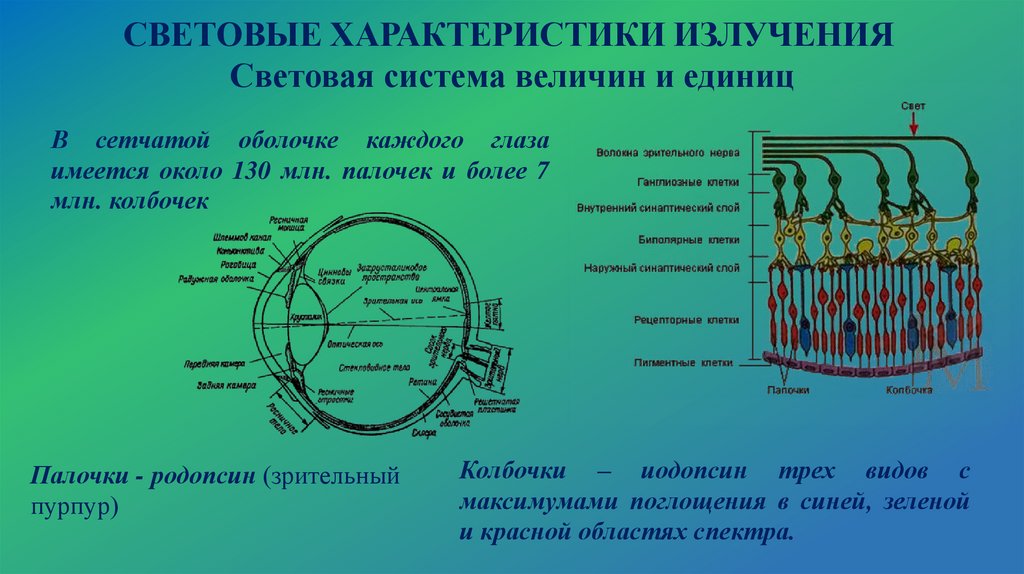
Строение человеческого глаза5.
Энергетическая яркость. Расчет облученности в фокальнойплоскости идеальной оптической системы
Aвх ОС
d >> f ’
F`
O
N
dA
Ω
α
Ie(α,β)
dA1
dAcos(α)
d
f’
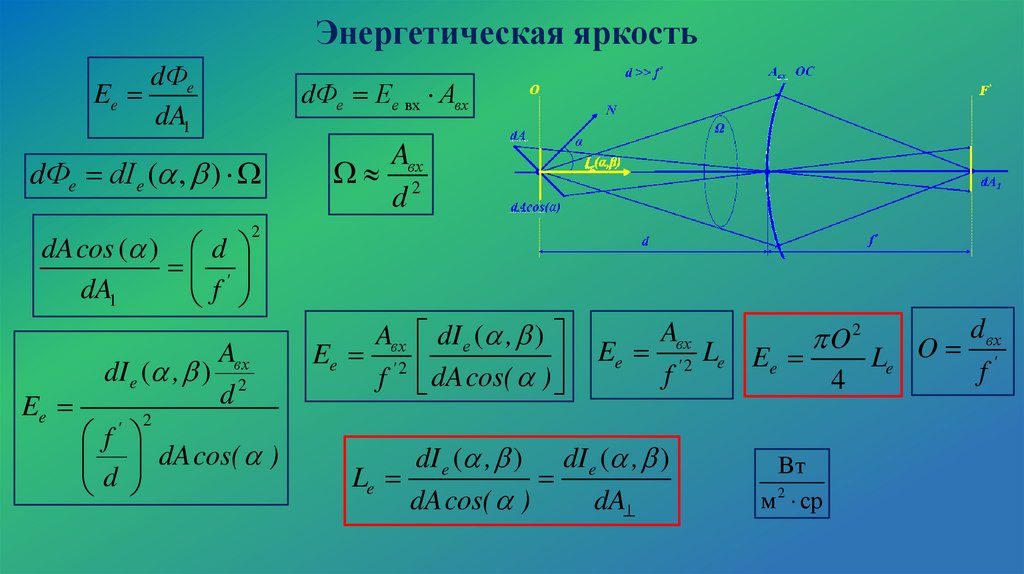
6.
Энергетическая яркостьdФe
Ee
dA1
dФе Ее вх Авх
dФe dI e ( , )
Aвх
2
d
dAcos ( ) d
'
dA1
f
2
Aвх
dI e ( , ) 2
d
Ee
' 2
f
dAcos( )
d
Aвх dI e ( , )
Ee ' 2
f dAcos( )
2
d вх
Aвх
O
Ee ' 2 Le Ee
Le O f '
f
4
dI e ( , ) dI e ( , )
Le
dAcos( )
dA
Вт
м 2 ср
7.
Энергетическая яркостьЭнергетическая яркость элемента поверхности (воображаемого или
реального) равна отношению его силы излучения в выбранном направлении к
площади проекции этой поверхности на плоскость, перпендикулярную
выбранному направлению ( dA ).
Физический смысл dA это видимая с выбранного
направления α,β площадь
элемента dA .
dI e ( , )
Le ( , ,x, y,z )
dA ( , ,x, y,z )
8.
Закон Ламберта. Светимость и яркость равнояркихисточников
Источники, яркость которых не зависит от выбранного в пространстве направления
излучают по закону Ламберта
I e ( , ) Le ( x, y, z ) dA cos( ) I e ( , ) I e 0 cos( )
Взаимосвязь яркости и светимости равноярких объектов
d 2Фе
dI e ( )
d
d 2Фe dI e ( )d
dI e ( )
Le
dI e ( ) Le dA cos( )
dA cos( )
d 2Фe 2 Le sin( ) cos( ) d dA
0
2
α α
dФe 2 Le dA sin( ) cos( ) d
0
d 2 sin( )d
π/2
dФ е
Me
dA
M e Le
9.
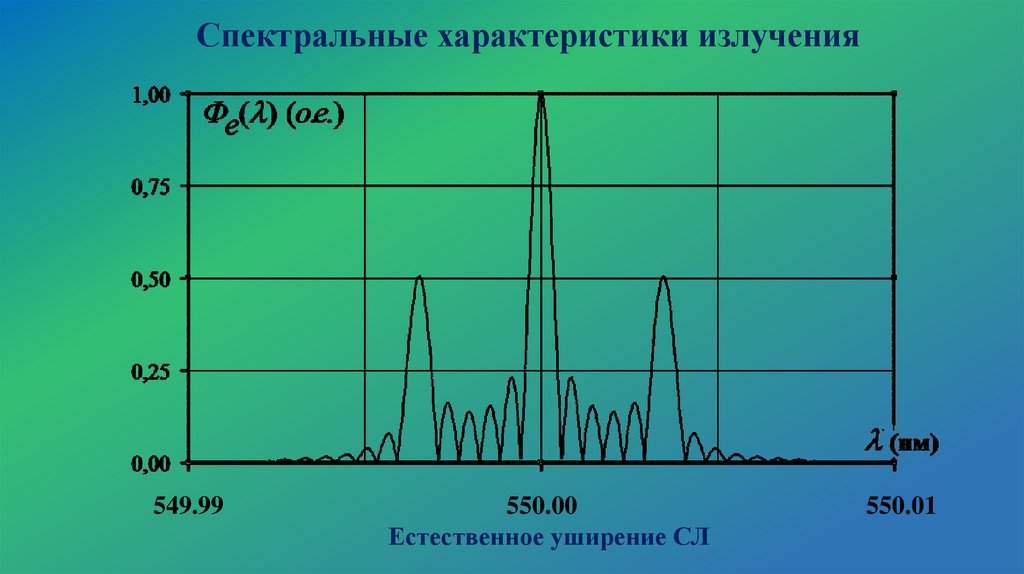
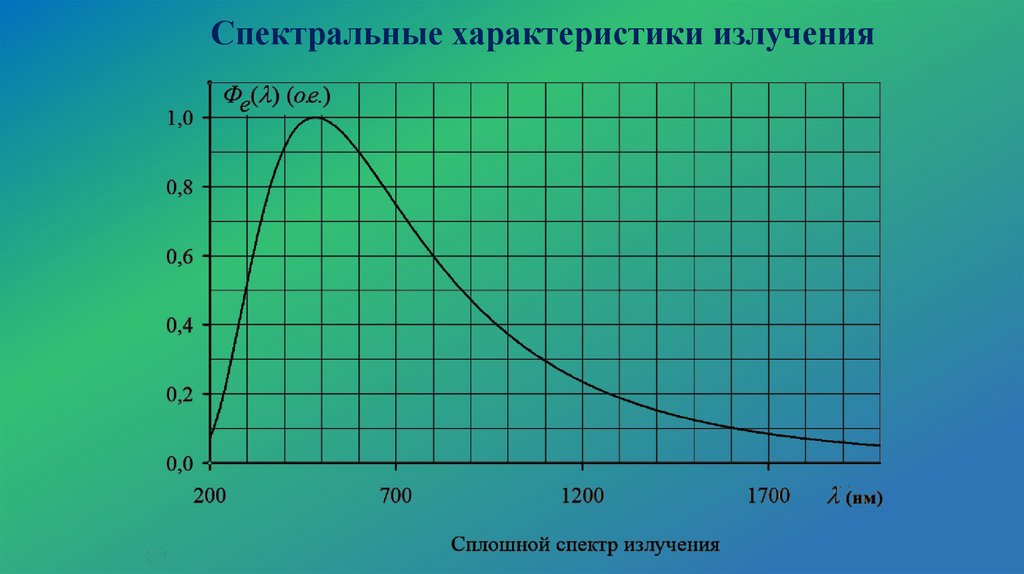
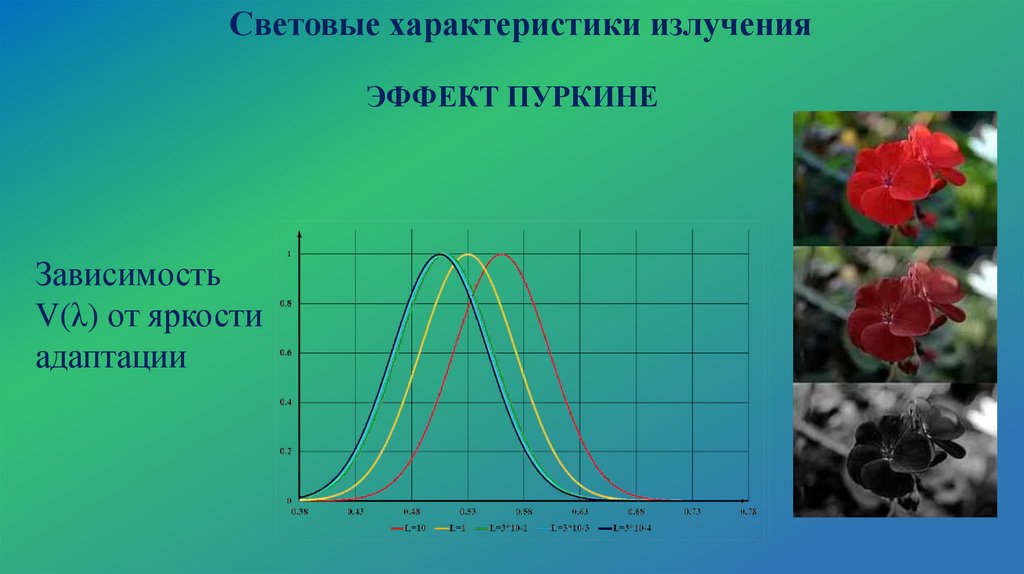
Спектральные характеристики излучения549.99
550.00
Естественное уширение СЛ
550.01
10.
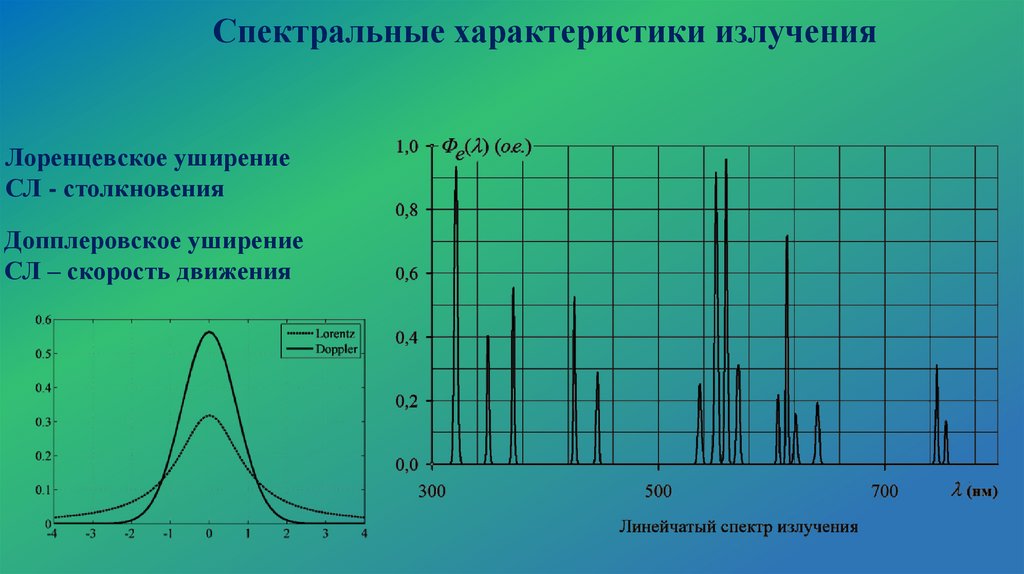
Спектральные характеристики излученияЛоренцевское уширение
СЛ - столкновения
Допплеровское уширение
СЛ – скорость движения
11.
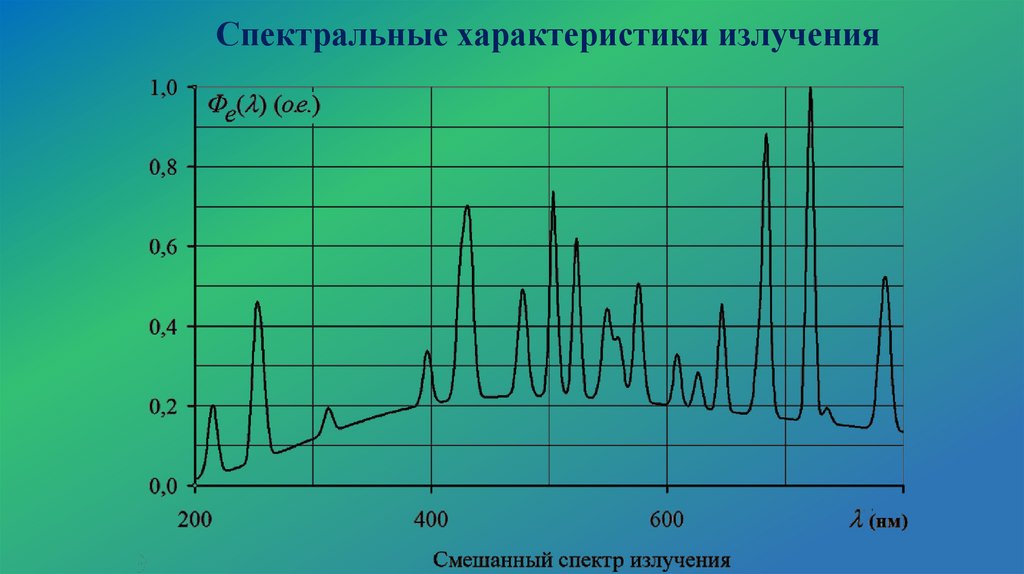
Спектральные характеристики излучения12.
Спектральные характеристики излучения13.
Спектральные характеристики излученияСпектральная плотность потока излучения Фе ( ) :
(Фе ; Ф, е ( , d ) )
Фе ( , )
dФе ( )
Фе ( ) lim
Фе ( )
0
d
Вт
м
Выражение монохроматического потока
излучения через его спектральную плотность
dФе ( ) Фе ( )d
1 мм
Фе
Ф ( ) d Ф ( ) d
е
1 нм
е
0
Вт
мкм
2
Вт
нм
Фе ( 1 , 2 ) Фе ( )d
1
14.
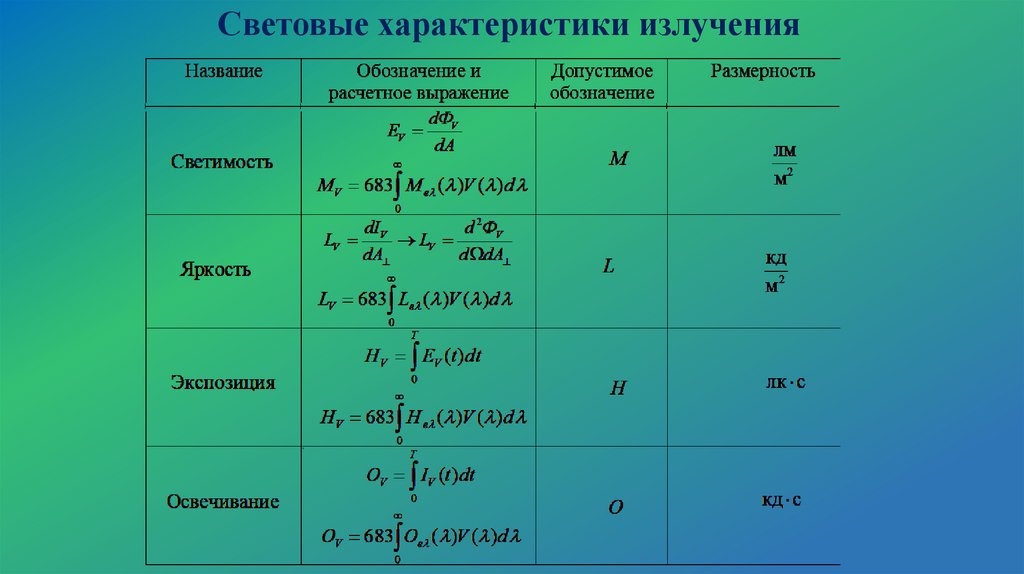
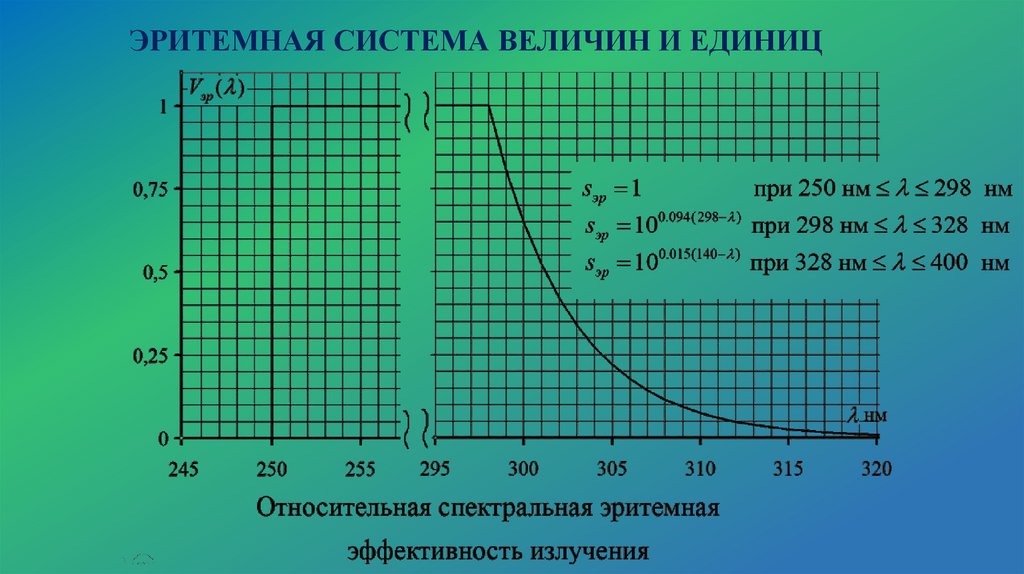
ЭНЕРГЕТИЧЕСКАЯ СИСТЕМА ВЕЛИЧИН И ЕДИНИЦ15.
Энергетическая система величин и единиц16.
ЭФФЕКТИВНЫЕ ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯТела, в которых происходит преобразование энергии излучения в другие виды
энергии, называются приемниками излучения.
Основные энергетические характеристики приемника излучения - его
спектральная и интегральная чувствительность.
Чувствительность приемника излучения – это отношение реакции
приемника излучения к величине входного воздействия, вызвавшего эту
реакцию.
Спектральная чувствительность приемника излучения – это
отношение реакции приемника излучения (R) к величине
монохроматического потока излучения (Фe(λ) ), вызвавшего эту реакцию:
R
S ( )
Фe ( )
dR
S ( )
dФe ( )
17.
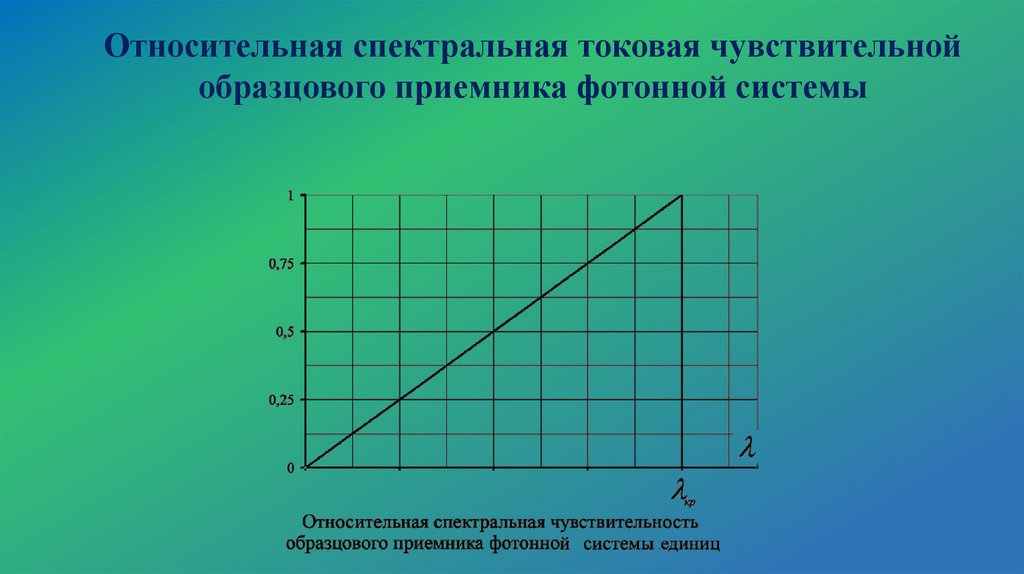
Эффективные характеристики излученияОтносительная спектральная чувствительность приемника
излучения:
S ( )
S 0 ( )
Smax
0
0
R Фe ( )S ( )d R S max Фe ( )S0 ( ) d
Интегральная чувствительность приемника излучения к
энергетическому потоку излучения:
Ф ( )S ( )d
R
Se
Se 0
Фe
e
Ф ( ) d
e
0
Ф ( )S ( )d
e
Se Smax 0
0
Ф ( ) d
e
0
18.
Эффективные характеристики излученияЭффективный (редуцированный) поток
излучения:
Фэф Фe ( )S0 ( )d
0
∞







































 Физика
Физика








