Тепловое излучение

1.

ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
Феи( М ) M eM (T ) AM
Ф
(M )
еп
EeM AM eM
Ф
(N )
еи
M eN (T ) AN
Феп( N ) EeN AN eN
M eM (T )
EeM
M eM (T ) AM EeM AM eM (T ) M eM (T ) EeM eM (T ) eM (T )
M eN (T ) AN EeN AN eN (T )
M eN (T ) EeN eN (T )
M eN (T )
EeN
eN (T )

2.

ТЕПЛОВОЕ ИЗЛУЧЕНИЕ
EeM EeN
M eM (T ) M eM (T )
eM (T ) eM (T )
M e1 (T ) M e 2 (T )
M ei (T )
M eS (T )
e1 (T ) e 2 (T )
ei (T )
С учетом второго закона термодинамики:
M e 1 ( , T ) M e 2 ( , T )
M e i ( , T )
M e S ( , T )
e1 ( , T )
e 2 ( , T )
ei ( , T )
Спектральная плотность излучения черного тела
c2
M e S ( , T ) c1T exp
T
3
1887 г., В. Михельсон
ν~V
2
6

3.

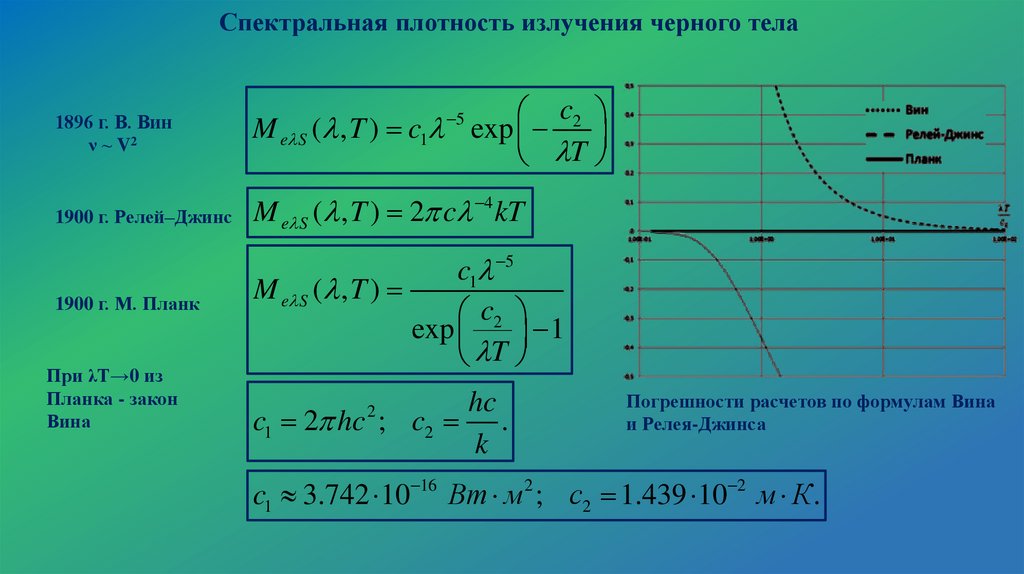
Спектральная плотность излучения черного тела
1896 г. В. Вин
ν ~ V2
c2
M e S ( , T ) c1 exp
T
1900 г. Релей–Джинс
M e S ( , T ) 2 c 4 kT
1900 г. М. Планк
c1 5
M e S ( , T )
c2
exp
1
T
При λT→0 из
Планка - закон
Вина
5
hc
c1 2 hc ; c2 .
k
2
Погрешности расчетов по формулам Вина
и Релея-Джинса
c1 3.742 10 16 Вт м 2 ; c2 1.439 10 2 м К .

4.

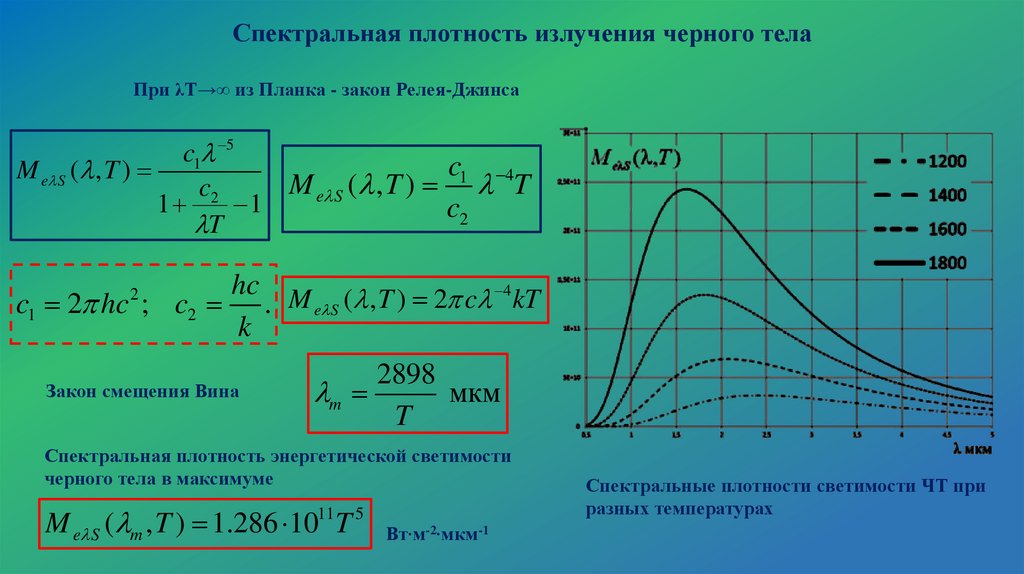
Спектральная плотность излучения черного тела
При λT→∞ из Планка - закон Релея-Джинса
c1 5
c1 4
M e S ( , T )
M e S ( , T ) T
c2
1
1
c2
T
hc M ( , T ) 2 c 4 kT
c1 2 hc ; c2 . e S
k
2
Закон смещения Вина
2898
m
мкм
T
Спектральная плотность энергетической светимости
черного тела в максимуме
M e S ( m , T ) 1.286 1011T 5
Вт∙м-2∙мкм-1
Спектральные плотности светимости ЧТ при
разных температурах

5.

Закон Стефана (1879) -Больцмана (1884) г.
Постоянная Стефана – Больцмана Получение закона Стефана – Больцмана из формулы Планка:

6.

Излучение черного тела
1. При повышении температуры излучающего тела происходит рост энергетической
светимости пропорционально четвертой степени температуры.
2. Максимум спектральной плотности энергетической светимости растет пропорционально
пятой степени температуры тела.
3. Повышение температуры тела приводит к смешению максимума кривой спектральной
плотности излучения в область коротких длин волн, следовательно к увеличению роли
коротковолновых излучений.
4. Максимум спектральной плотности излучения черного тела лежит в видимой области
спектра (λ=0,38÷0,78 мкм) для значений температур 3715÷7626 К°.

7.

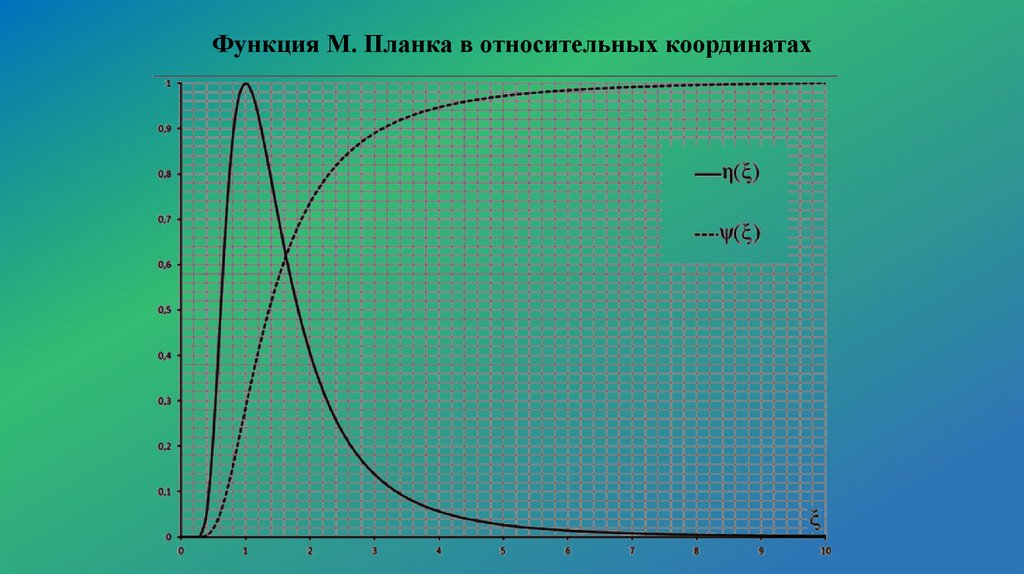
Функция М. Планка в относительных координатах
λ2
M
eλS
(λ, T )dλ
λ
0
η(ξ)dξ
ξ
ηs (λ1 ,λ 2 ) = 1
M
ξ
ξ2
= 1
eλS
(λ, T )dλ
η(ξ)dξ
0
= ( 2 ) ( 1 )
η(ξ)dξ
(ξ)= 0
η(ξ)dξ
0

8.

Функция М. Планка в относительных координатах

9.

Тепловое излучение реальных тел
При отсутствии многократных отражений
Спектральный коэффициент
излучения
Интегральный коэффициент
излучения
Следствие закона
Кирхгофа
При наличии многократных отражений
- Спектральный коэффициент почернения

10.

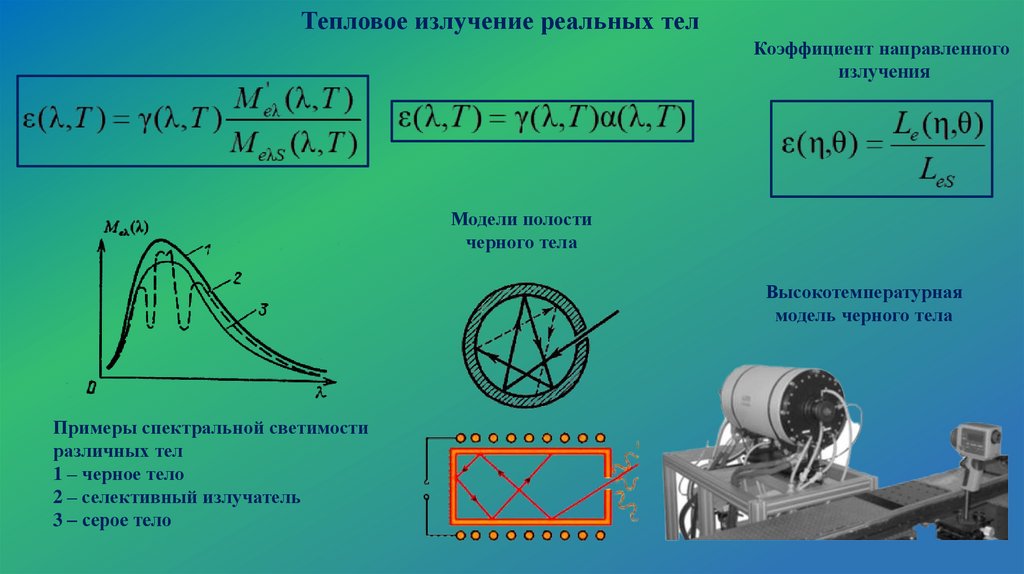
Тепловое излучение реальных тел
Коэффициент направленного
излучения
Модели полости
черного тела
Высокотемпературная
модель черного тела
Примеры спектральной светимости
различных тел
1 – черное тело
2 – селективный излучатель
3 – серое тело

11.

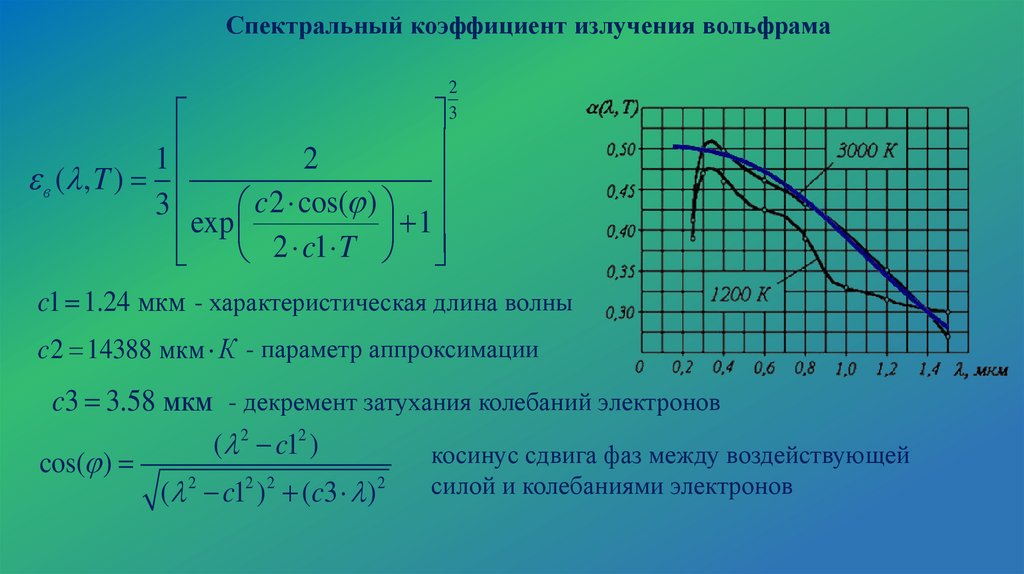
Спектральный коэффициент излучения вольфрама
1
2
в ( , T )
3
c 2 cos( )
exp
1
2 c1 T
2
3
c1 1.24 мкм - характеристическая длина волны
c 2 14388 мкм К - параметр аппроксимации
c3 3.58 мкм - декремент затухания колебаний электронов
( 2 c12 )
косинус сдвига фаз между воздействующей
cos( )
силой и колебаниями электронов
( 2 c12 ) 2 (c3 ) 2

12.

Тепловое действие излучения
Уравнение теплового баланса
e 0 Ee A0 dt cmdT ak (T Tв ) Adt
поглощенная
энергия
энергия
затраченная
на нагрев
отведенная за счет
конвекци энергия
(T то e 0 T от eт ) Adt
uAdt
изменение энергии за счет
теплообмена излучением
энергия , затраченная
на испарение ( сушку )
4
4
т
αe0, αem – коэффициенты поглощения
тела и окружающих предметов
Tв – температура воздуха
A0 – облучаемая площадь
A – полная площадь тела
c – удельная теплоемкость тела
φ – удельная теплота испарения
ηоп – коэффициент использования
потока объекта окружающими телами
u – скорость испарения
m – плотность тела
ak – коэффициент теплопередачи конвекцией

13.

Тепловое действие излучения
При Т<700K
(T 4 то e 0 Tт4 от eт ) Adt ak (T Tв ) Adt aT (T Tв )
aТ – суммарный коэффициент теплопередачи
с
e 0 Ee A0 dt a A dT aT a A (T Tв )dt ua Adt
aV
где
где
a A A A0 ; aV A V ; плотность тела

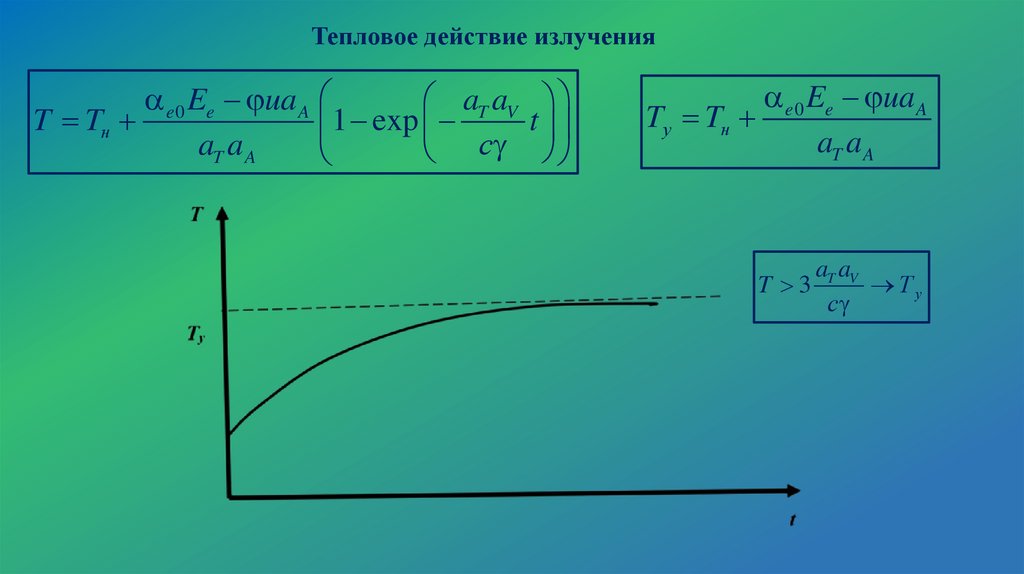
14.

Тепловое действие излучения
e 0 Ee ua A
aT aV
T Tн
t
1 exp
aT a A
с
e 0 Ee ua A
Tу Tн
aT a A
aT aV
T 3
Ту
с

15.

ЭКВИВАЛЕНТНЫЕ ТЕМПЕРАТУРЫ
Эквивалентной температурой (Тэк) называется температура черного тела, при которой одна из его
фотометрических характеристик совпадает с аналогичной характеристикой реального тела имеющего
температуру Т. Используются следующие эквивалентные температуры: Тр, Тя, Тц, Ткц
Радиационная температура (Тр)
M eS ( Tp ) M e ( T )
Tр T
Схема радиационного пирометра
с одноэлементным приемником
излучения.
1 – объектив; 2 – диафрагма;
3 – термоэлемент;
4 –светофильтр;
5 – окуляр
Современный тепловизор
1 – объектив; 2 – жидкокристаллический экран
3 – электронный блок с болометрической матрицей

16.

ЭКВИВАЛЕНТНЫЕ ТЕМПЕРАТУРЫ
Яркостная температура (Тя)
LeS ( я ,Tp ) Le ( я ,T )
я 660 нм
c2
c2
5
c exp
я , Т c1 я exp
яTя
яT
5
1 я
Tя
c2
1
я c2 ln , Т
я
яT
Tя T

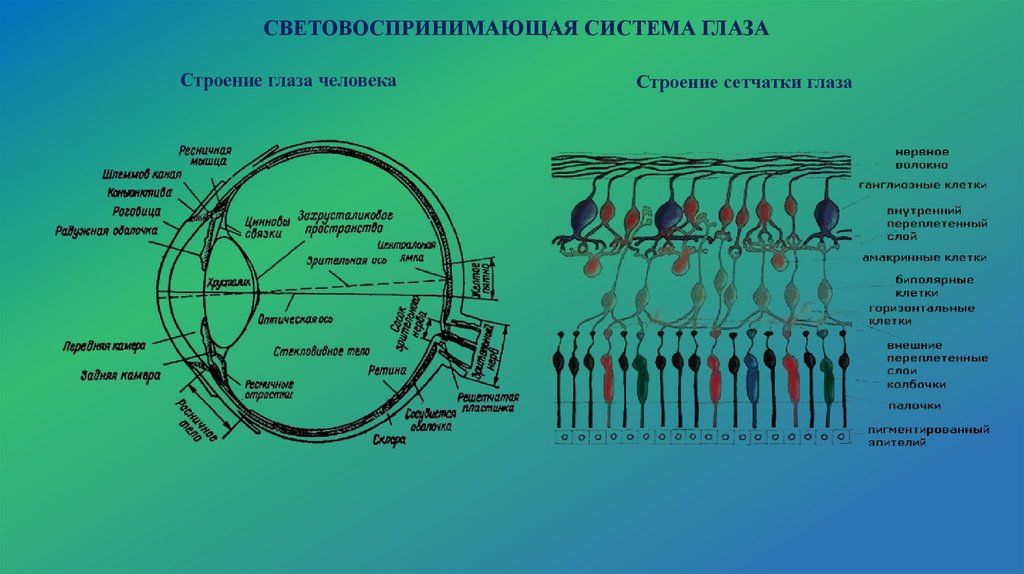
17.

СВЕТОВОСПРИНИМАЮЩАЯ СИСТЕМА ГЛАЗА
Строение глаза человека
Строение сетчатки глаза

18.

РАСЧЕТ ЦВЕТОВЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ
Эффективные потоки рецепторов
Спектральные
чувствительности колбочек
Фк к Фе ( )к ( )d
380
780
Фз з Фе ( ) з ( )d
380
780
Фс с Фе ( )с ( )d
380
780
Удельные координаты цвета
к ( ); з ( ); с ( )
Фv 683 Фк Фз Фс
Lv 683 Lк Lз Lс
780
780
780
Lv 683 к Lе ( )к ( )d з Lе ( ) з ( )d с Lе ( )с ( ) d
380
380
380

19.

РАСЧЕТ ЦВЕТОВЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ
Для монохроматического излучения
Треугольник
единичных цветов
Фv 683Фе ( )V ( )
Фv 683 к к ( ) з з ( ) с с ( ) Фе ( )
Цветовое пространство
Джеймс Клерк Максвелл
1860 год
V ( ) к к ( ) з з ( ) с с ( )
К ( )
Фe ( )
З ( )
з ( )
Фe ( )
С ( )
с ( )
Фe ( )
Координаты цвета
к ( )
К Фе ( )к ( )
З Фе ( ) з ( )
С Фе ( )с ( )
Цвет F(К,З,С) характеризуется длиной
(модулем σF) и направлением в цветовом
пространстве (координатами цветности
к, з, с)
К З С
к
К
К
К З С
З
З
К З С
С
С
с
К З С
з
Физическое содержание
удельных координат цвета:
координаты цвета
монохроматического
излучения мощностью 1 Вт
совпадают с удельными
координатами цвета

20.

РАСЧЕТ ЦВЕТОВЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ
к з с 1
Для излучения сложного
спектрального состава
К Фе ( )к ( )d
380
780
З Фе ( ) з ( )d
380
780
С Фе ( )с ( )d
380
Совокупность к, з для всех возможных излучений
образуют диаграмму цветности, т.е. область реальных
цветов
780
Законы Грассмана
1. Любой цвет может быть получен алгебраическим сложением в
определенных количествах трех линейно независимых основных цветов
Цветовое уравнение:
F К К З З СС
2. При непрерывном изменении спектрального состава любого
излучения цвет меняется непрерывно
3. Цвет смеси цветов зависит только от цветов,
составляющих (компонентов) смеси и не зависит от
спектрального состава излучения:
Следствие: существуют так называемые
«метамерные цвета», имеющие разные
спектральные распределения, но одинаковый цвет
N
К см К i
i 1
N
Зсм Зi
i 1
N
Ссм Сi
i 1

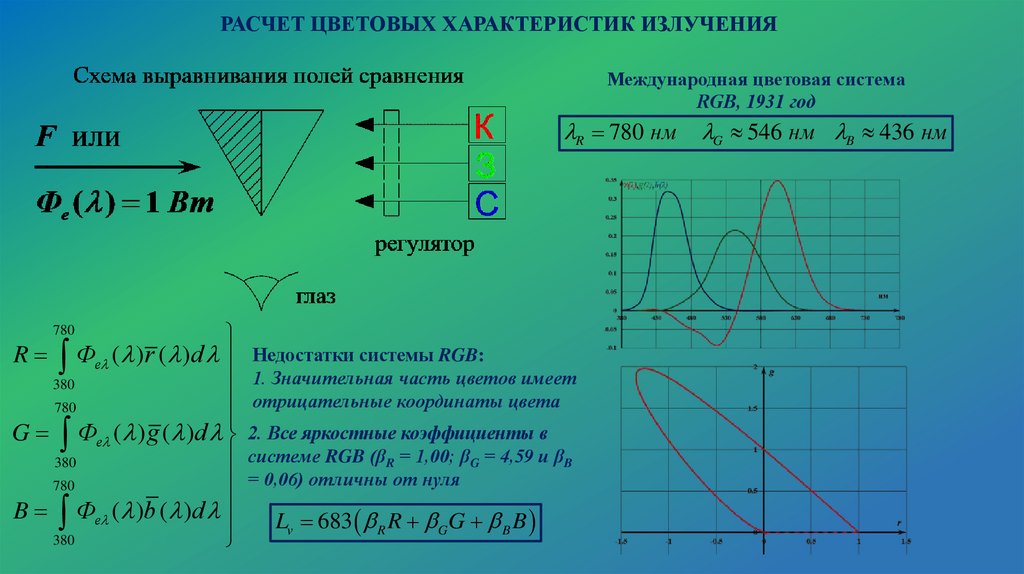
21.

РАСЧЕТ ЦВЕТОВЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ
Международная цветовая система
RGB, 1931 год
R 780 нм G 546 нм B 436 нм
R Фе ( )r ( )d Недостатки системы RGB:
380
1. Значительная часть цветов имеет
780
отрицательные координаты цвета
G Фе ( ) g ( )d 2. Все яркостные коэффициенты в
380
системе RGB (βR = 1,00; βG = 4,59 и βB
780
= 0,06) отличны от нуля
B Фе ( )b ( )d
Lv 683 R R G G B B
380
780

22.

РАСЧЕТ ЦВЕТОВЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ
Требования к новой системе:
1. Удельные координаты цвета должны быть
положительны для всех реальных цветов → Основные
цвета системы – нереальные цвета
2. Яркостной коэффициент только у одного цвета
должен быть отличен от нуля
X Фе ( ) x ( )d
380
780
Y Фе ( ) y ( )d
380
780
Z Фе ( ) z ( )d
380
780
Международная цветовая система
XYZ, 1931 год
βX = 0; βY= 1; βZ = 0
Lv 683 X X L Y YL Z Z L
Lv 683YL
Фv 683YФ
y ( ) V ( )
2.768505 0.999935 0.000055
x (λ) y (λ) z (λ) r (λ) g (λ)b (λ) 1.751491 4.589942 0.056629
1.130003 0.060123 5.593316
0.000902
0.418762 0.09117
r (λ) g (λ)b (λ) x (λ) y (λ) z (λ) 0.15887 0.252449 0.00251
0.0829
0.015708 0.178602

23.

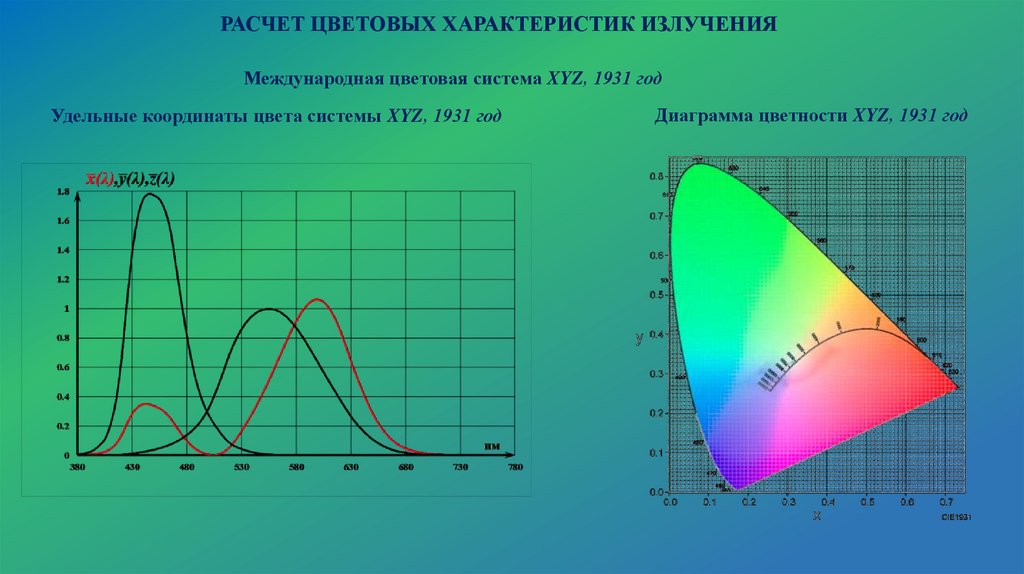
РАСЧЕТ ЦВЕТОВЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ
Международная цветовая система XYZ, 1931 год
Удельные координаты цвета системы XYZ, 1931 год
Диаграмма цветности XYZ, 1931 год

24.

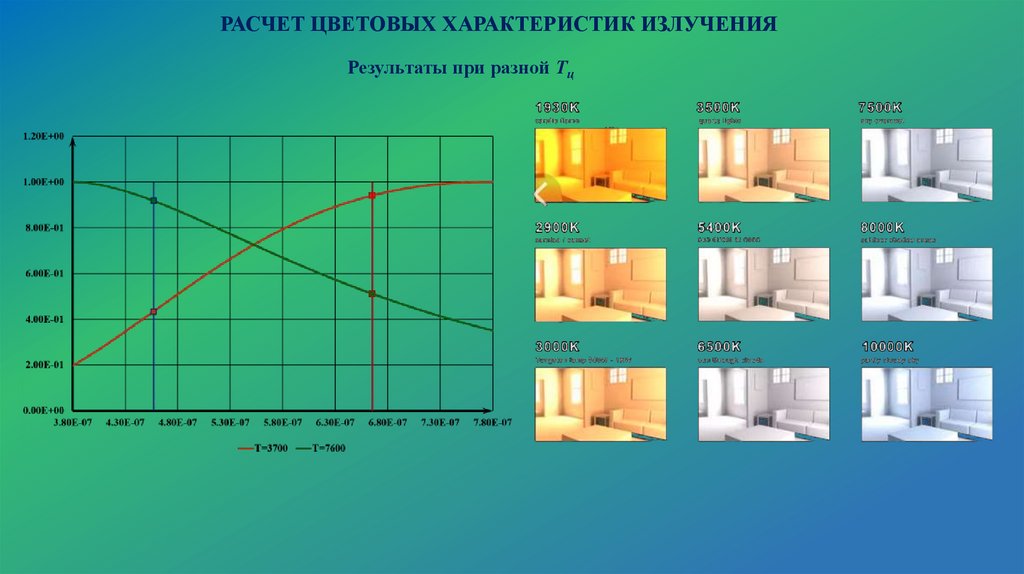
РАСЧЕТ ЦВЕТОВЫХ ХАРАКТЕРИСТИК ИЗЛУЧЕНИЯ
Результаты при разной Тц

25.

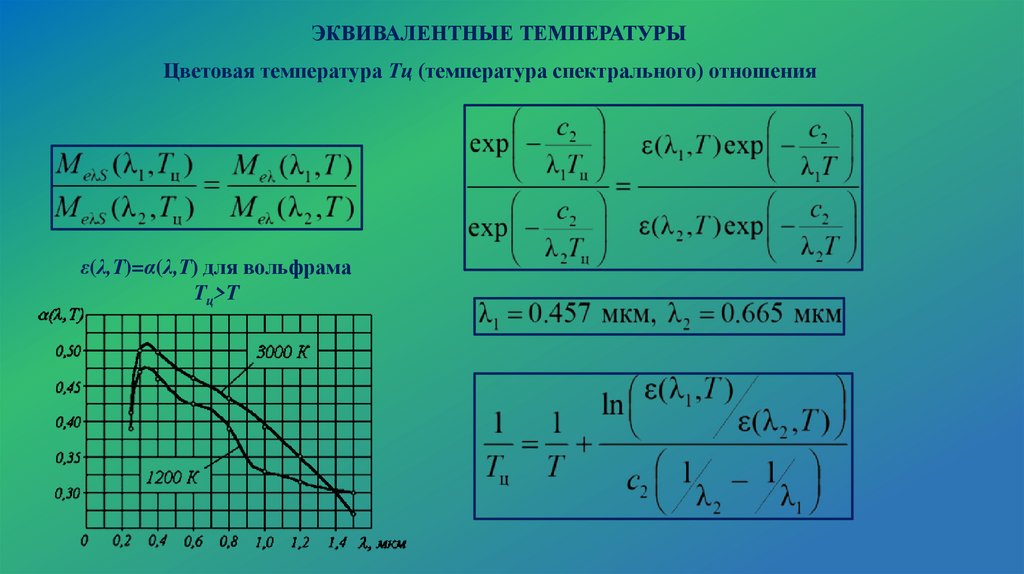
ЭКВИВАЛЕНТНЫЕ ТЕМПЕРАТУРЫ
Цветовая температура Тц (температура спектрального) отношения
ε(λ,Т)=α(λ,Т) для вольфрама
Тц>T

26.

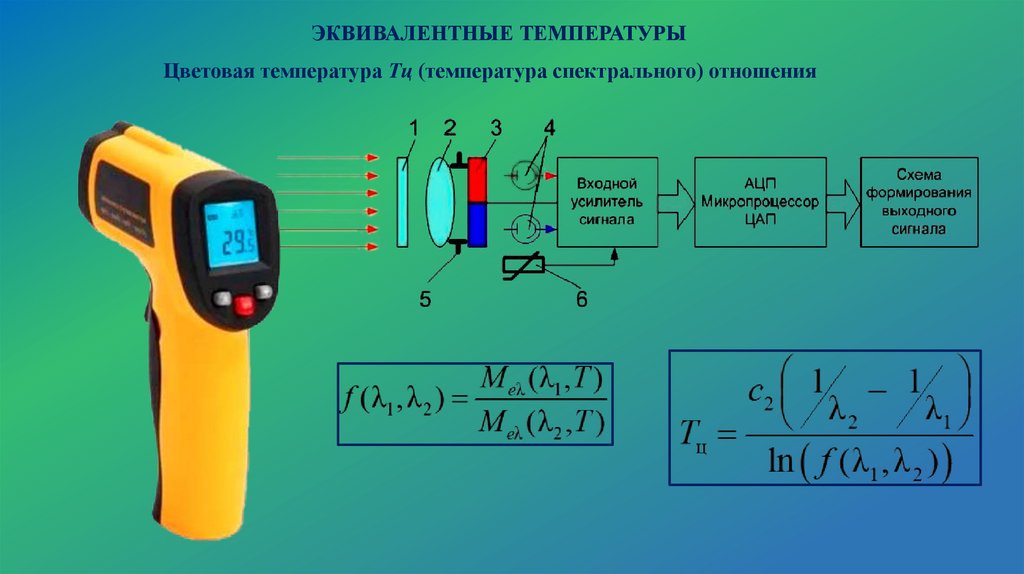
ЭКВИВАЛЕНТНЫЕ ТЕМПЕРАТУРЫ
Цветовая температура Тц (температура спектрального) отношения

27.

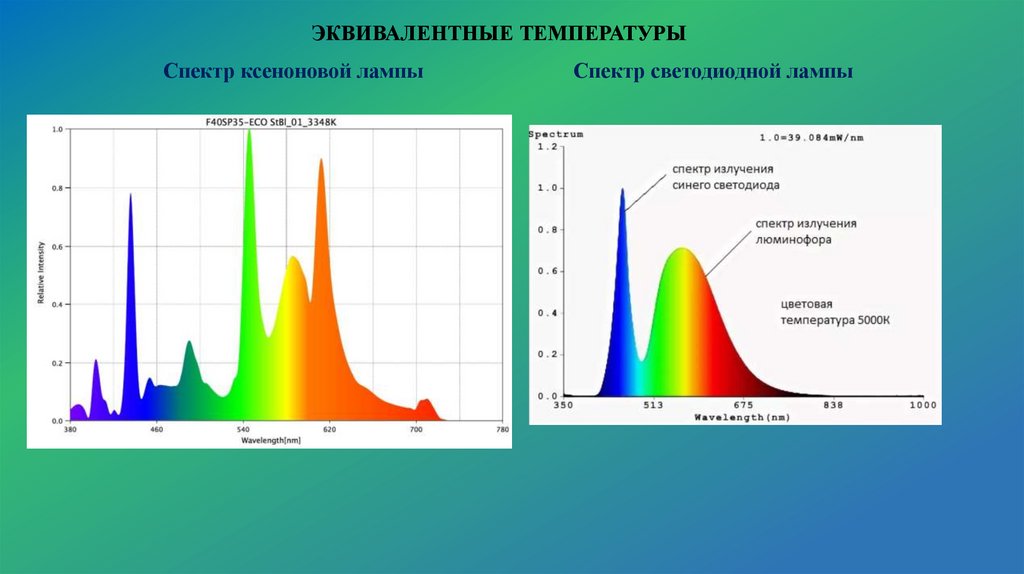
ЭКВИВАЛЕНТНЫЕ ТЕМПЕРАТУРЫ
Спектр ксеноновой лампы
Спектр светодиодной лампы

28.

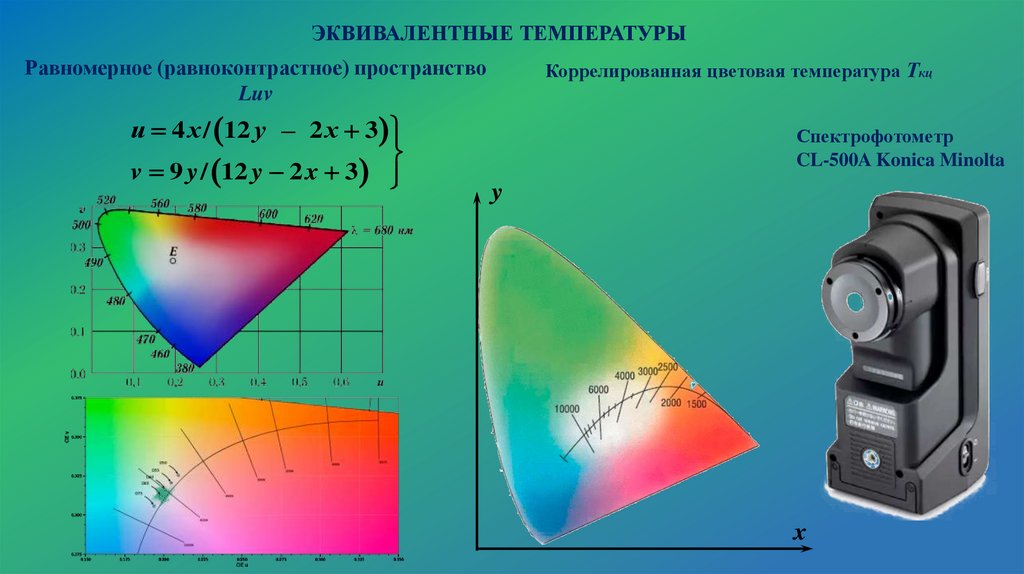
ЭКВИВАЛЕНТНЫЕ ТЕМПЕРАТУРЫ
Равномерное (равноконтрастное) пространство
Luv
u 4 x / 12 y – 2 x 3
v 9 y / 12 y 2 x 3
Коррелированная цветовая температура Ткц
Спектрофотометр
CL-500A Konica Minolta
y
x