Похожие презентации:
Двогранний кут. Перпендикулярні площини
1.
2.
3.
4.
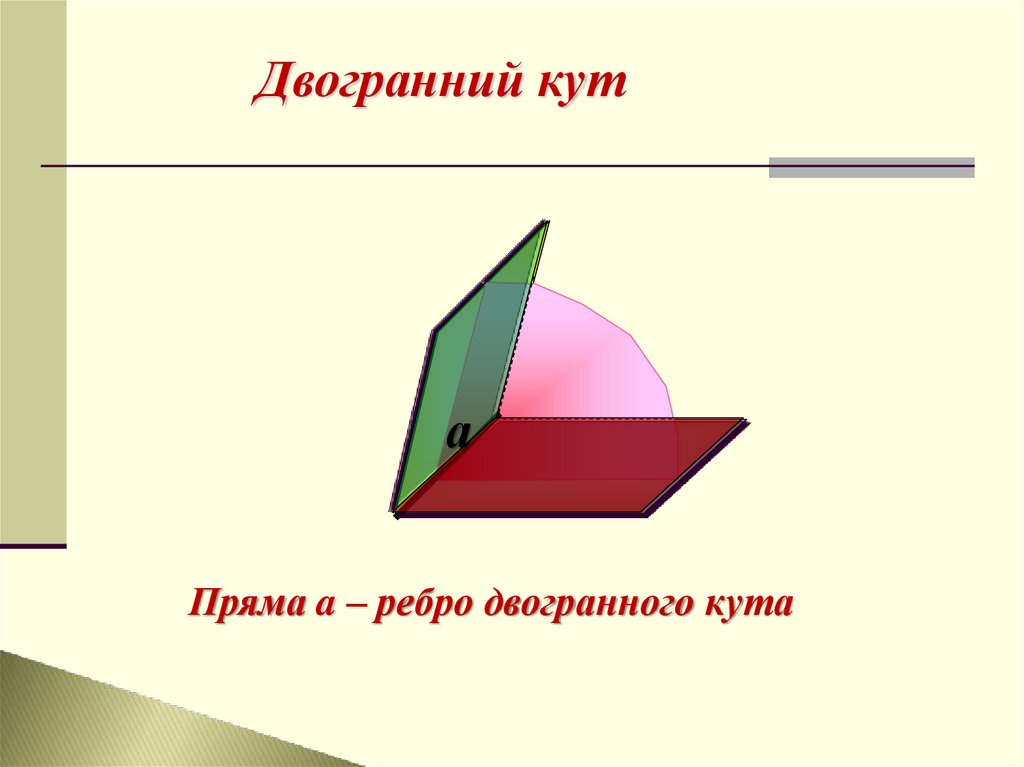
Двогранний кута
Пряма a – ребро двогранного кута
5.
6.
Всі лінійні кути двогранногокута рівні!
O
А
А1
В
O1
В1
7.
8.
Яким може бути взаємне розміщеннядвох площин в просторі?
α
α
α║β
с
β
β
α∩β=с
8
9.
Тема уроку:9
10. Означення перпендикулярних площин
Дві площини, що перетинаються, називаютьсяперпендикулярними, якщо третя площина,
перпендикулярна до прямої перетину цих площин,
перетинає їх по перпендикулярних прямих.
Якщо α∩β=с,
∩α=а, ∩β=b,
с ┴ і а ┴ b, то
α ┴β
b
β
с
α
а
10
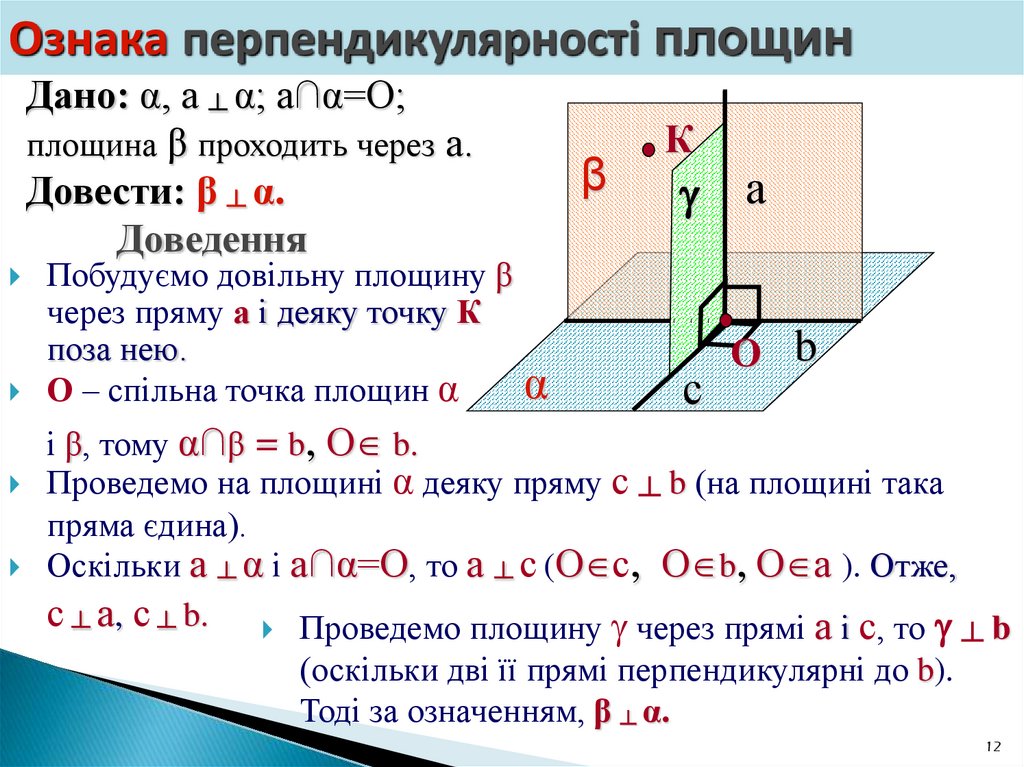
11. Ознака перпендикулярності площин
Якщо одна з двох площин проходитьчерез пряму, перпендикулярну до другої
площини, то ці площини перпендикулярні.
Дано: α, а ┴ α;
а∩α=О; площина β
проходить через а.
Довести: β ┴ α.
β
α
а
О
b
11
12. Ознака перпендикулярності площин
Дано: α, а ┴ α; а∩α=О;площина β проходить через а.
Довести: β ┴ α.
Доведення
Побудуємо довільну площину β
через пряму а і деяку точку К
поза нею.
α
О – спільна точка площин α
β
К
с
а
О b
і β, тому α∩β = b, О b.
Проведемо на площині α деяку пряму с ┴ b (на площині така
пряма єдина).
Оскільки а ┴ α і а∩α=О, то а ┴ с (О с, О b, О а ). Отже,
с ┴ а, с ┴ b. Проведемо площину через прямі а і с, то
(оскільки дві її прямі перпендикулярні до b).
Тоді за означенням, β ┴ α.
┴b
12
13. Властивості перпендикулярних площин
Якщо дві площини взаємно перпендикулярні, тобудь-яка пряма, що лежить в одній з них і
перпендикулярна до їхньої лінії, перпендикулярна
до другої площини.
β
Дано: а ┴ b, α∩β=с,
а1 α і а1┴с, с∩а1=А.
Довести: а1 ┴ β
b
b1
А
а α
с
а1
13
14. Властивості перпендикулярних площин
Якщо дві площини взаємно перпендикулярні та здеякої точки однієї з них опущено перпендикуляр
на другу, то цей перпендикуляр лежить у першій
площині.
Дано: α ┴ β, α∩β=с,
А β, В α,
АВ ┴ α.
β
b
А
а α
Довести: АВ β
с
В
14
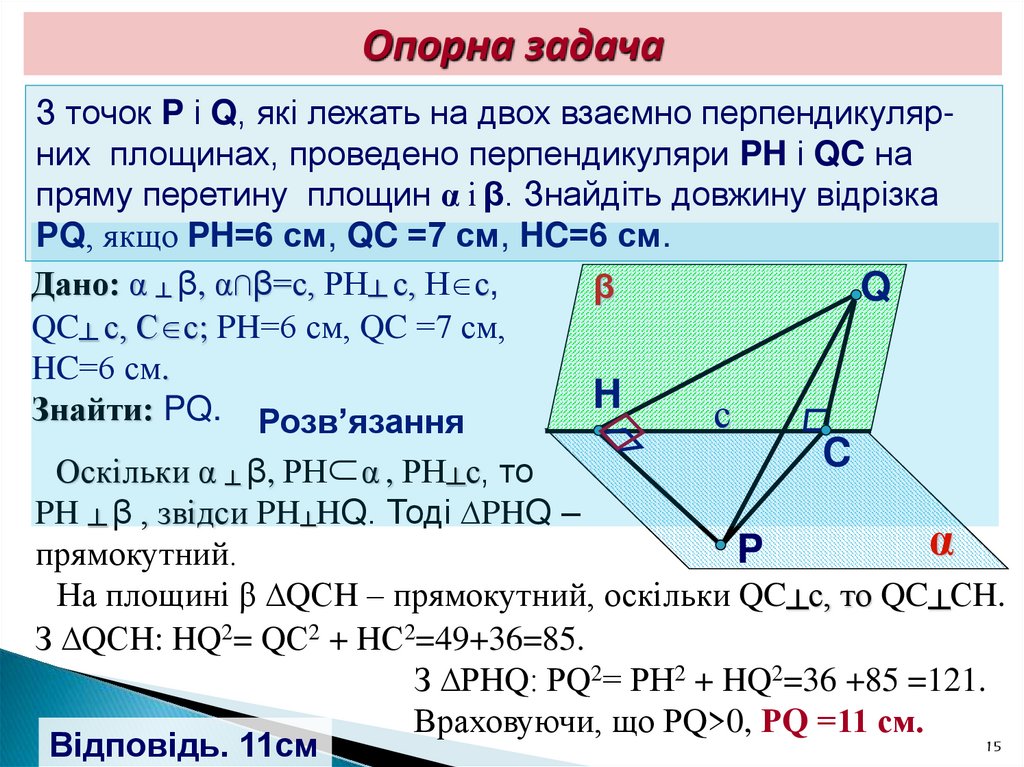
15. Опорна задача
З точок P і Q, які лежать на двох взаємно перпендикулярних площинах, проведено перпендикуляри PH і QC напряму перетину площин α і β. Знайдіть довжину відрізка
PQ, якщо PH=6 см, QC =7 см, HC=6 см.
Дано: α ┴ β, α∩β=с, РН┴ с, Н с,
β
Q
QC┴ с, С с; PH=6 см, QC =7 см,
HC=6 см.
H
Знайти: PQ. Розв’язання
с
C
Оскільки α ┴ β, РН α , РН┴с, то
PH ┴ β , звідси PH┴HQ. Тоді ∆PHQ –
α
P
прямокутний.
На площині β ∆QСH – прямокутний, оскільки QC┴с, то QC┴СH.
З ∆QСH: HQ2= QС2 + HС2=49+36=85.
З ∆РHQ: РQ2= РН2 + HQ2=36 +85 =121.
Враховуючи, що РQ>0, РQ =11 см.
15
Відповідь. 11см
16. Підсумки уроку Контрольні запитання:
• Подивіться, чи є на вашу думку, перпендикулярніплощини в класній кімнаті?
• Перерізом куба площиною, перпендикулярною
до його грані є…
квадрат.
• Дано куб ABCDA1B1C1D1 (див. мал. 5.39 ст.169).
Площина ВDD1 ┴ … до площини
C1CD;
C1B1B;
C1CB;
C1D1B1.
16













 Математика
Математика








