Метод перемещений

1.

© Себешев В.Г., 2022
СТРОИТЕЛЬНАЯ МЕХАНИКА
Часть II
СТАТИЧЕСКИ
НЕОПРЕДЕЛИМЫЕ
СИСТЕМЫ
Расчёт деформируемых систем
методом перемещений
1

2.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Метод перемещений –
метод расчёта деформируемых систем,
в котором за основные неизвестные принимаются
характерные перемещения,
после определения которых все перемещения
и силовые факторы
в рассчитываемой системе могут быть найдены
стандартными процедурами (поэлементно).

3.

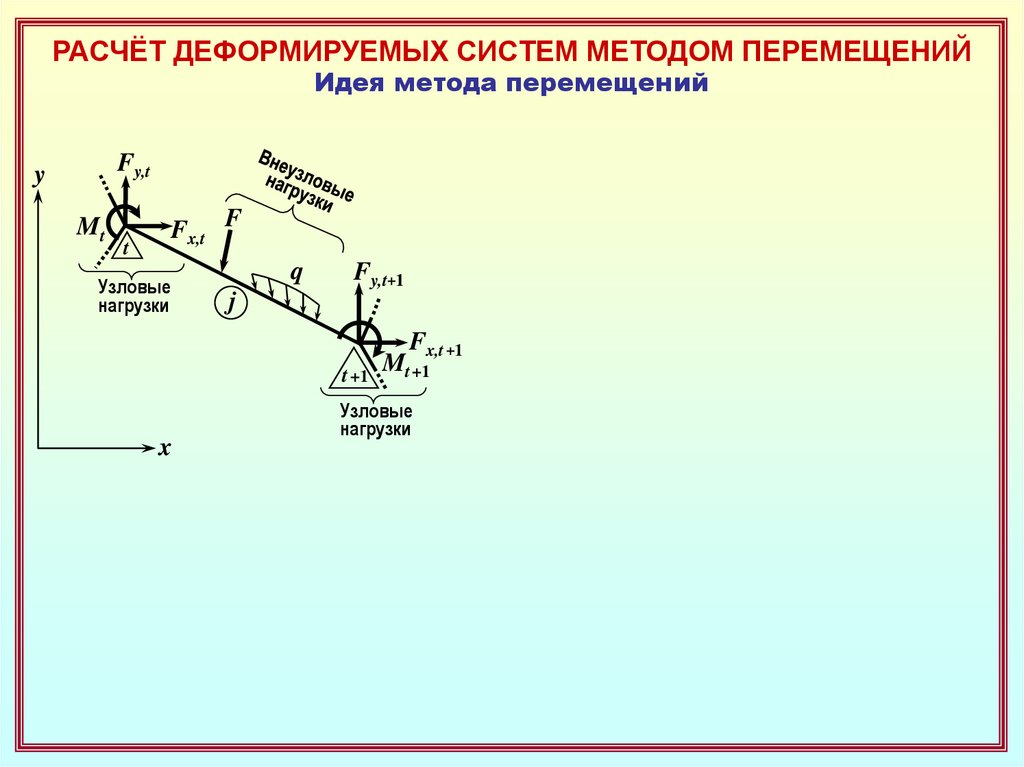
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
Fy,t
y
Mt
t
Fx,t F
Узловые
нагрузки
q
Fy,t+1
j
Fx,t +1
t +1
x
Mt +1
Узловые
нагрузки

4.

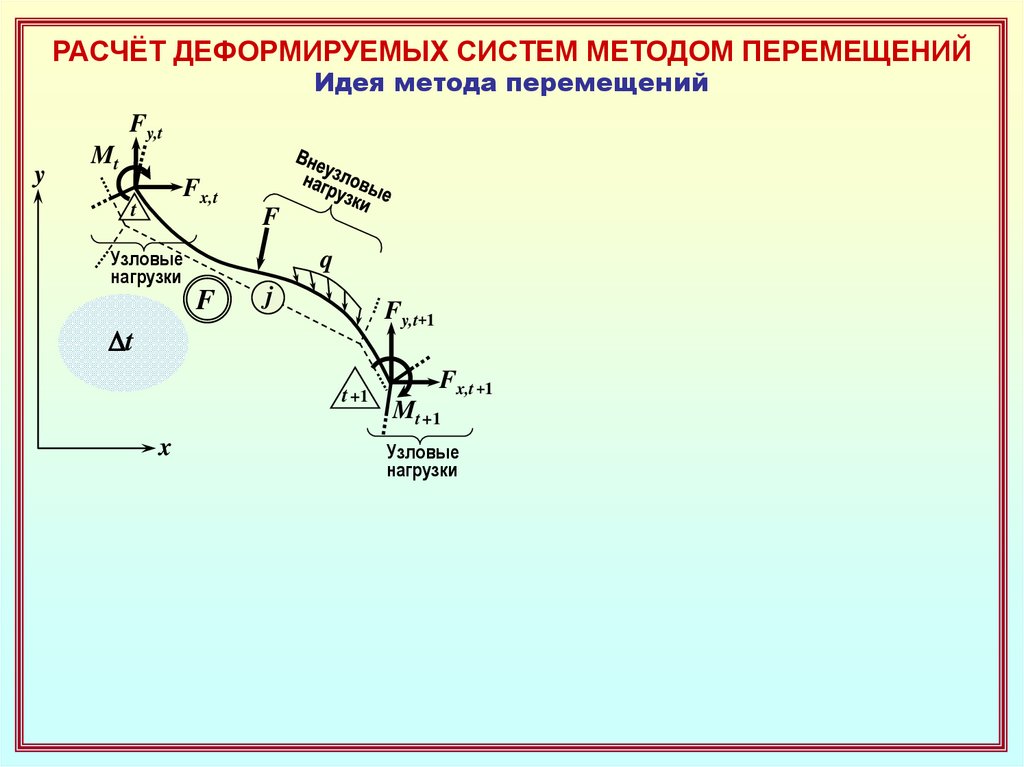
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
Fy,t
y
Mt
Fx,t
t
F
Узловые
нагрузки
q
F
j
Fy,t+1
Dt
t +1
x
Fx,t +1
Mt +1
Узловые
нагрузки

5.

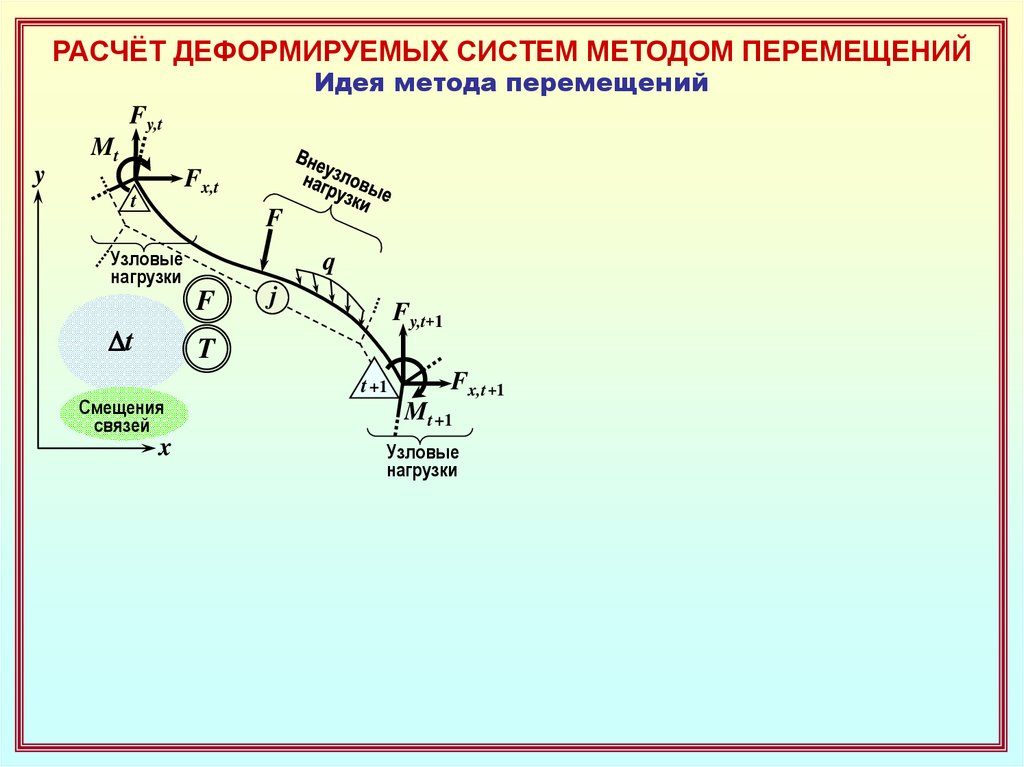
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
Fy,t
y
Mt
Fx,t
t
F
Узловые
нагрузки
q
F
Dt
j
Fy,t+1
T
Смещения
связей
x
t +1
Fx,t +1
Mt +1
Узловые
нагрузки

6.

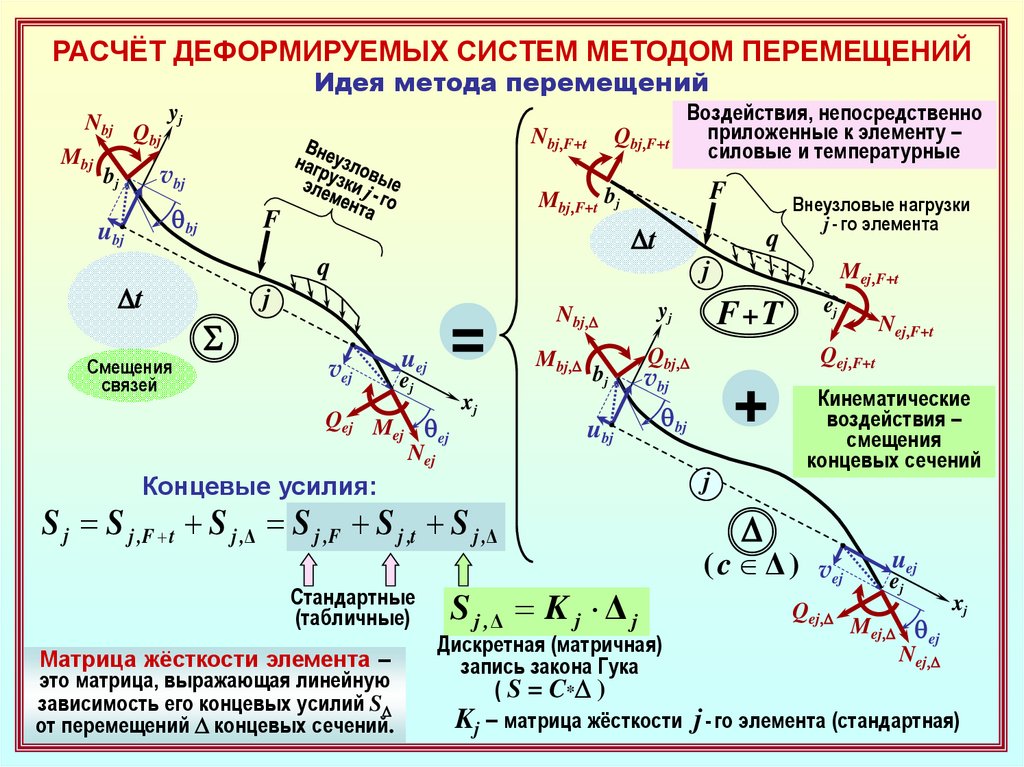
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
Mt
y
Mbj
Fx,t
t
F
Узловые
нагрузки
Dt
Смещения
связей
Вектор перемещений
концевых сечений
j - го элемента: θ
Nbj Q yj
bj
Fy,t
bj
vbj
ubj
qbj
F
q
F
j
T
S
с
Qbj
x N bj
M bj
bj
Вариант представления
концевых усилий: M bj
Q bj
S bj N bj
Sj
M
S
ej
ej
Q
ej
N ej
j
Вектор усилий
в концевых сечениях
(концевых усилий)
j - го элемента: M bj
Fy,t+1
yj
Mt +1
Узловые
нагрузки
F
q
j
vej
uej
Q bj
xj
S bj N bj Q
Sj
ej Mej q
ej
S
M
ej
ej
N
ej
Q ej
N
Для линейно
ej
деформируемых
систем ( Л Д С ):
Правила знаков
усилий
S j S j дляиконцевых
перемещений:
Fx,t +1
t +1
bj
vbj
Δ
u
Δ j Δ bj θ bj
ej ej
vej
q
uej
ej
положительными считаются
M , q – по ходу часовой стрелки;
M ej
Qej
ej
xj
N ej
Q , v – сдвиг по часовой стрелке;
N , u – по внешней нормали
к сечению

7.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
Nbj Q yj
bj
Mbj
bj
vbj
ubj
qbj
F
Mbj,F+t bj
F
Dt
q
q
Dt
Смещения
связей
Qbj,F+t
Nbj,F+t
Воздействия, непосредственно
приложенные к элементу –
силовые и температурные
j
j
S
vej
=
uej
ej
Qej M q
ej
ej
Nej
Nbj,D
Mbj,D
bj
xj
ubj
Концевые усилия:
Стандартные
(табличные)
Mej,F+t
F+T
yj
S j ,Δ K j Δ j
ej
Nej,F+t
Qej,F+t
Qbj,D
vbj
+
qbj
j
S j S j ,F t S j ,Δ S j ,F S j ,t S j ,Δ
Матрица жёсткости элемента –
это матрица, выражающая линейную
зависимость его концевых усилий SD
от перемещений D концевых сечений.
Внеузловые нагрузки
j - го элемента
Кинематические
воздействия –
смещения
концевых сечений
D
( c Δ ) vej
Qej,D
uej
ej
xj
Mej,D qej
Дискретная (матричная)
Nej,D
запись закона Гука
( S = C*D )
Kj – матрица жёсткости j - го элемента (стандартная)

8.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
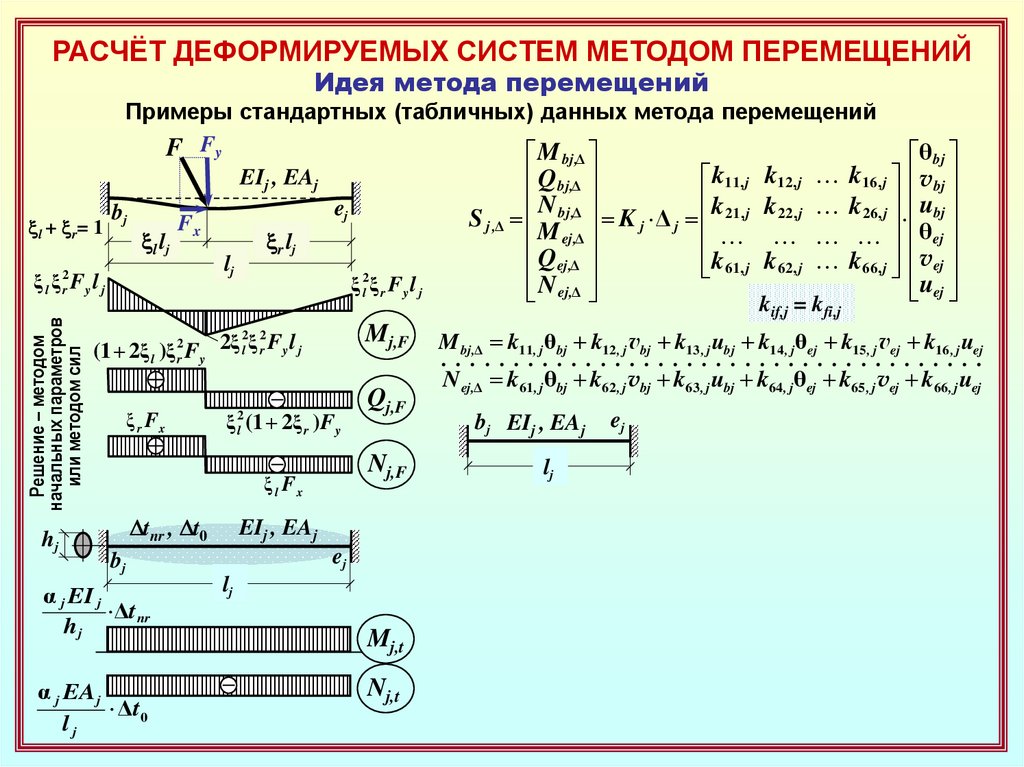
Примеры стандартных (табличных) данных метода перемещений
EIj , EAj
ej
bj
lj

9.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
Решение – методом
начальных параметров
или методом сил
Примеры стандартных (табличных) данных метода перемещений
F Fy
M bj,Δ
θ bj
EIj , EAj
k11, j k12, j k16, j vbj
Q bj,Δ
k 21, j k 22, j k 26, j ubj
N bj,Δ
ej
bj
S j ,Δ
K j Δ j
Fx
xl + xr= 1
M ej,Δ
θ ej
xl lj
xr lj
k
v
Q
k
k
ej,Δ
l
61,
j
62,
j
66,
j
j
ej
2
ξ l ξ 2r Fy l j
ξ l ξ r Fy l j
uej
N ej,Δ
kif,j = kfi,j
hj
Mj,F
(1 2ξ l )ξ 2r Fy 2ξ l ξ r Fy l j
2 2
ξ r Fx
ξ (1 2ξ r )Fy
2
l
Nj,F
ξ l Fx
Dtnr , Dt0
EIj , EAj
ej
bj
α j EI j
Δt nr
hj
α j EA j
Δt 0
lj
Qj,F
lj
Mj,t
Nj,t
M bj,Δ k11, j θbj k12 , j vbj k13 , j ubj k14 , j θej k15 , j vej k16 , j uej
......................................
N ej,Δ k61, j θbj k62 , j vbj k63 , j ubj k64 , j θej k65 , j vej k66 , j uej
bj EIj , EAj
lj
ej

10.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
Решение – методом
начальных параметров
или методом сил
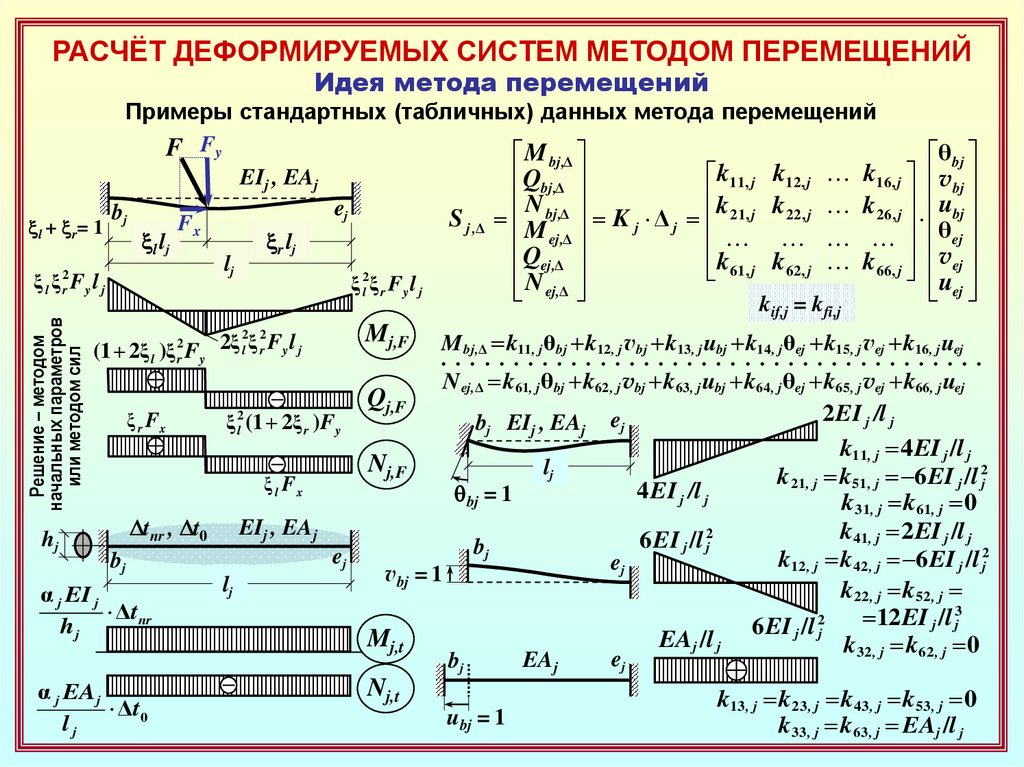
Примеры стандартных (табличных) данных метода перемещений
F Fy
M bj,Δ
θ bj
k11, j k12, j k16, j vbj
EIj , EAj
Qbj,Δ
k
N bj,Δ
k 22, j k 26, j ubj
ej
bj
21,
j
S j ,Δ M K j Δ j
Fx
θ
xl + xr= 1
ej,Δ
xl lj
xr lj
vej
Q
ej,Δ
lj
k61, j k62, j k66, j ej
2
ξ l ξ 2r Fy l j
ξ l ξ r Fy l j
N ej,Δ
uej
kif,j = kfi,j
hj
Mj,F
(1 2ξ l )ξ 2r Fy 2ξ l ξ r Fy l j
2 2
ξ r Fx
ξ (1 2ξ r )Fy
2
l
α j EA j
Δt 0
lj
qbj = 1
EIj , EAj
ej
bj
α j EI j
Δt nr
hj
j
Nj,F
ξ l Fx
Dtnr , Dt0
Qj,F
M bj,Δ k11, j θbj k12 , j vbj k13 , j ubj k14 , j θej k15 , j vej k16 , j uej
......................................
N ej,Δ k61, j θbj k62 , j vbj k63 , j ubj k64 , j θej k65 , j vej k66 , j uej
2 EI j /l j
b EI , EA ej
lj
j
lj
4 EI j /l j
bj
vbj = 1
Mj,t
j
bj
Nj,t
ubj = 1
ej
EAj
ej
6 EI j /l 2j
EA j /l j
k11, j 4 EI j /l j
k 21, j k51, j 6 EI j /l 2j
k31, j k61, j 0
k41, j 2 EI j /l j
k12 , j k 42 , j 6 EI j /l 2j
k22 , j k52 , j
12 EI j /l 3j
6 EI j /l 2j
k32 , j k62 , j 0
k13 , j k23 , j k43 , j k53 , j 0
k 33 , j k63 , j EAj /l j

11.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
Структура матрицы жёсткости элемента
при растяжении (сжатии) и изгибе в одной плоскости
M bj,...
Q bj,...
N bj,...
M ej,... =
Q ej,...
N ej,...
От uej = 1
От vej = 1
От qej = 1
От ubj = 1
От vbj = 1
От qbj = 1
k11, j k12, j k13, j k14, j k15, j k16, j
k 21, j k 22, j k 23, j k 24, j k 25, j k 26, j
k
31, j k 32, j k 33, j k 34, j k 35, j k 36, j
K j
k
k
k
k
k
k
41, j 42, j 43, j 44, j 45, j 46, j
k51, j k52, j k53, j k54, j k55, j k56, j
k61, j k62, j k63, j k64, j k65, j k66, j
4 EI j /l j 6 EI j /l 2j
0
2 EI j /l j 6 EI j /l 2j
0
6 EI /l 2 12 EI /l 3
0
6 EI j /l 2j 12 EI j /l 3j
0
j j
j j
0
0
EA
/
l
0
0
EA
/
l
j
j
j
j
2
2
0
4 EI j /l j 6 EI j /l j
0
2 EI j /l j 6 EI j /l j
6 EI j /l 2j 12 EI j /l 3j
0
6 EI j /l 2j 12 EI j /l 3j
0
0
0
EA
/
l
0
0
EA
/
l
j
j
j
j

12.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
Векторы концевых усилий и перемещений и матрица жёсткости
прямолинейного пространственно деформируемого стержня постоянного сечения
Sj = [ Mz, bj My, bj Mt, bj Qz, bj Qy, bj Nbj Mz, ej My, ej Mt, ej Qz, ej Qy, ej Nej ]т
Dj = [ qz, bj qy, bj qt, bj vz, bj vy, bj ubj qz, ej qy, ej qt, ej vz, ej vy, ej uej ]т
4 iz
0
0
0 6 i z l 1 0
2 iz
0
0
0 6i z l 1 0 M z,bj,...
0
4iy
0 6 i y l 1 0
0
0
2iy
0 6i y l 1 0
0 M y, bj,...
1
1
0
0
GI
l
0
0
0
0
0
GI
l
0
0
0
t
t
M t,bj,...
0
0
0 6 i y l 1 0 12 i y l 2 0
0 Qz,bj,...
0 6 i y l 1 0 12 i y l 2
6 i z l 1 0
0
0 12 i z l 2 0 6 i z l 1 0
0
0 12 i z l 2 0 Q y, bj,...
1
1 N
0
0
0
0
0
EAl
0
0
0
0
0
EAl
bj,...
K j
1
1
0
0
0 6 iz l
0
4 iz
0
0
0 6 iz l
0 M z,ej,...
2 iz
0
2iy
0 6 i y l 1 0
0
0
4iy
0 6 i y l 1 0
0 M y, ej,...
0
0 GI t l 1 0
0
0
0
0 GI t l 1 0
0
0 M t,ej,...
1
2
1
2
0
6
i
l
0
12
i
l
0
0
0
6
i
l
0
12
i
l
0
0
y
y
y
y
Qz,bj,...
0
0 12 i z l 2 0 6 i z l 1 0
0
0 12 i z l 2 0 Q y, bj,...
6 i z l 1 0
1
1 N
0
0
0
0
0
EAl
0
0
0
0
0
EAl
ej,...
iz = EIz,j / lj
iy = EIy,j / lj
– погонные изгибные жёсткости стержня в главных плоскостях инерции

13.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
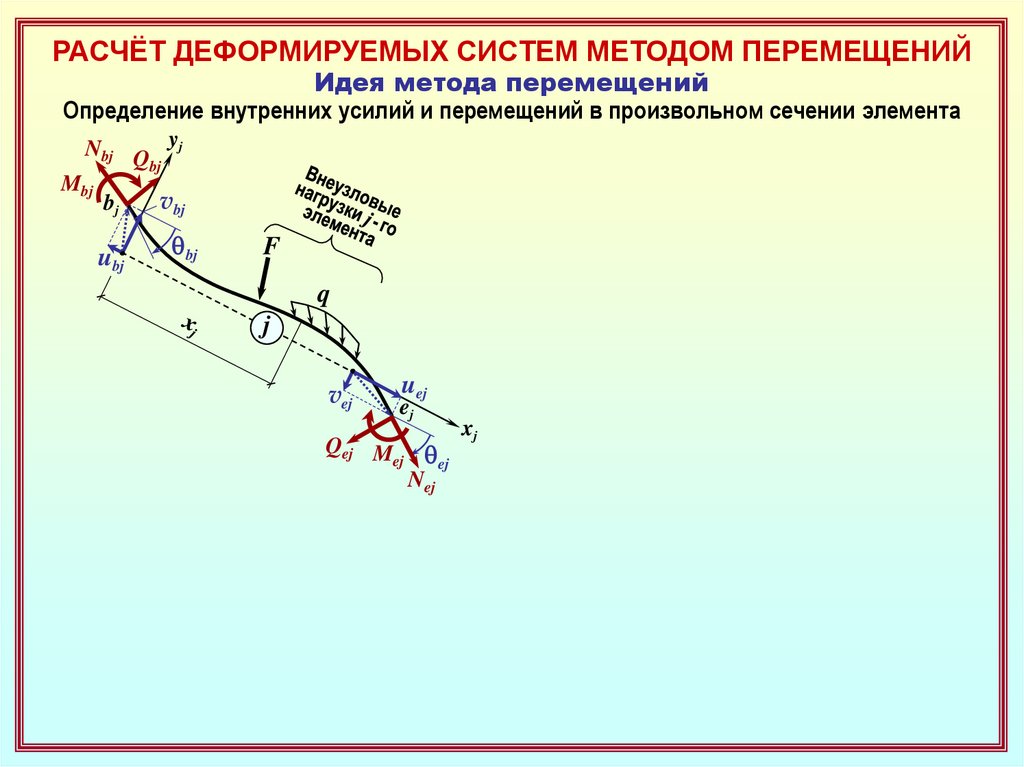
Определение внутренних усилий и перемещений в произвольном сечении элемента
Nbj Q yj
bj
Mbj
bj
vbj
ubj
qbj
F
q
j
vej
uej
ej
Qej M q
ej
ej
Nej
xj

14.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
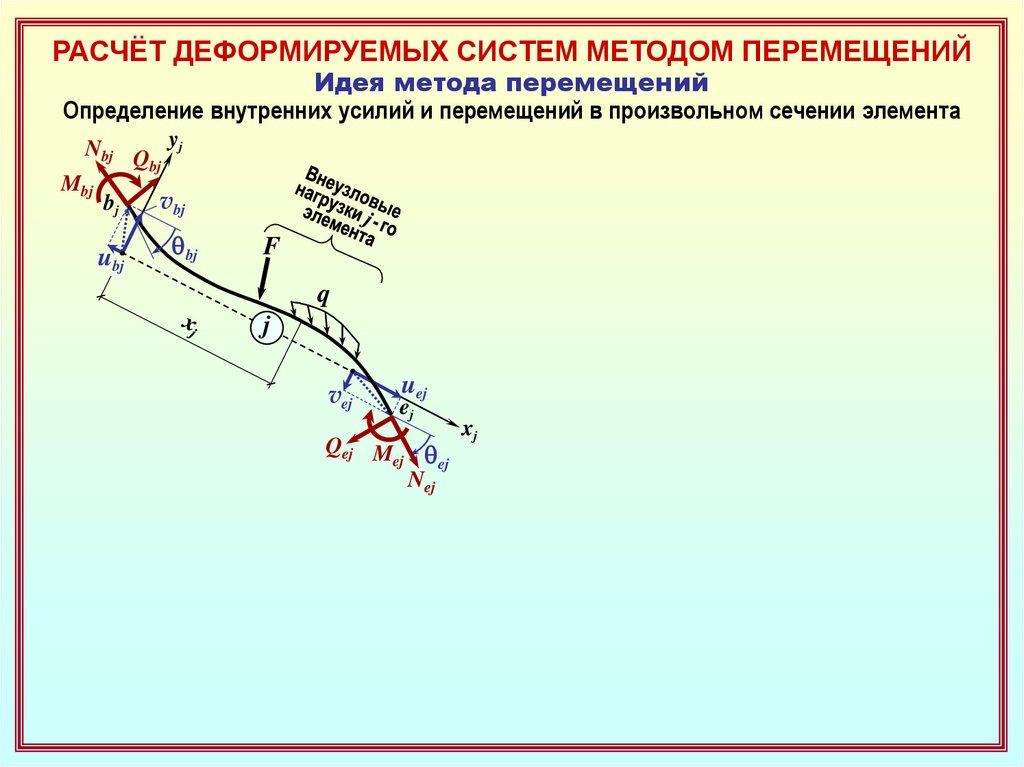
Определение внутренних усилий и перемещений в произвольном сечении элемента
Nbj Q yj
bj
Mbj
bj
vbj
ubj
qbj
F
q
j
vej
uej
ej
Qej M q
ej
ej
Nej
xj

15.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
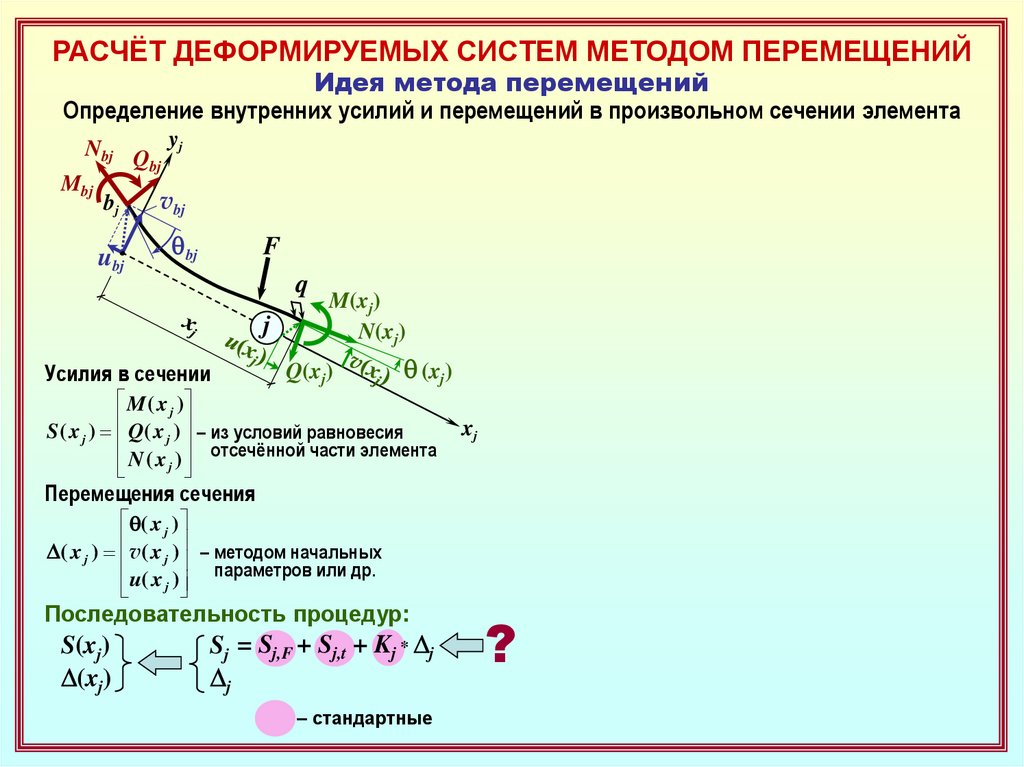
Определение внутренних усилий и перемещений в произвольном сечении элемента
Nbj Q yj
bj
Mbj
bj
vbj
ubj
qbj
F
q
j
Усилия в сечении
M(xj)
N(xj)
Q(xj)
q (xj)
M ( x j )
S ( x j ) Q( x j ) – из условий равновесия
отсечённой части элемента
N ( x j )
xj
Перемещения сечения
q( x j )
D ( x j ) v( x j ) – методом начальных
параметров или др.
u( x j )
Последовательность процедур:
S(xj)
D(xj)
Sj = Sj,F + Sj,t + Kj * Dj
Dj
– стандартные
?

16.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
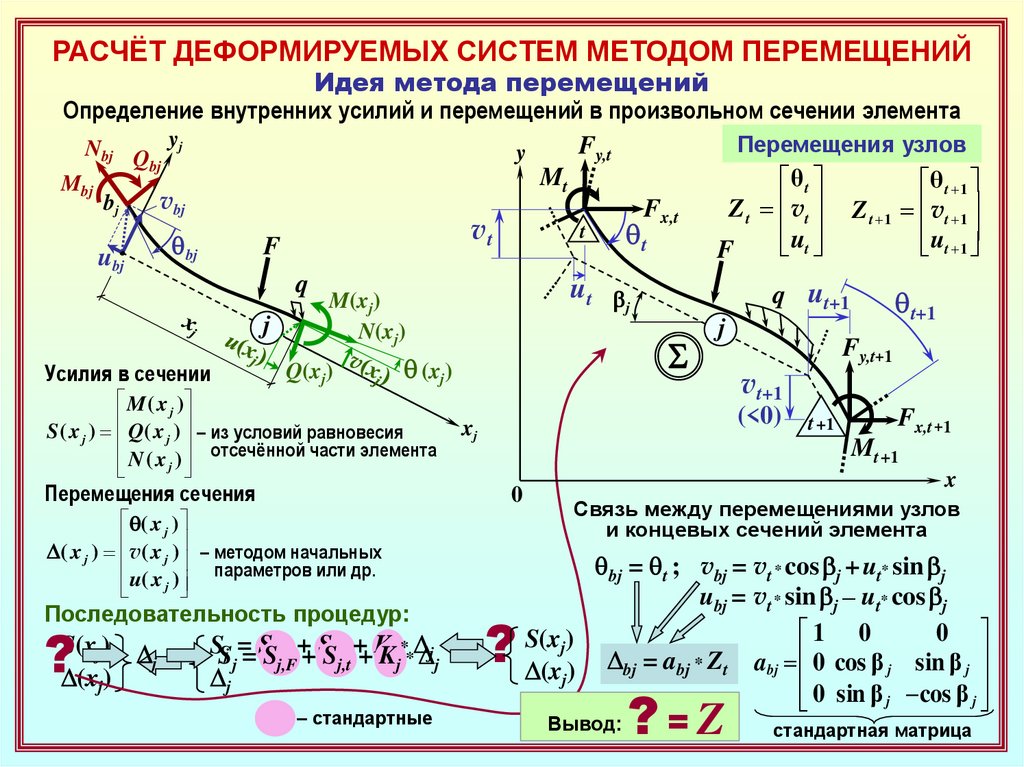
Определение внутренних усилий и перемещений в произвольном сечении элемента
Перемещения узлов
Fy,t
Nbj Q yj
y
bj
Mt
θ t
θ t 1
Mbj
v
bj
bj
Fx,t
Z t vt Z t 1 vt 1
t
u
vt
u
qt
t
F
q
t 1
F
bj
ubj
q
ut
q u
j
Усилия в сечении
bj
M(xj)
N(xj)
Q(xj)
S
q (xj)
M ( x j )
S ( x j ) Q( x j ) – из условий равновесия
отсечённой части элемента
N ( x j )
Перемещения сечения
?
SSj == SSj,F ++ SSj,t ++ KKj **DDj
j
j,F
j,t
j
j
Dj
– стандартные
Fy,t+1
vt+1
(<0)
t +1
Fx,t +1
Mt +1
q( x j )
D ( x j ) v( x j ) – методом начальных
параметров или др.
u( x j )
S(xj) D
j
D(xj)
j
xj
0
Последовательность процедур:
qt+1
t+1
?
x
Связь между перемещениями узлов
и концевых сечений элемента
qbj = qt ; vbj = vt * cos bj + ut* sin bj
ubj = vt * sin bj – ut* cos bj
1 0
0
S(xj)
D(xj) Dbj = abj * Zt abj 0 cos β j sin β j
0 sin β j cos β j
Вывод:
?=Z
стандартная матрица

17.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Идея метода перемещений
За основные неизвестные в методе перемещений принимаются
независимые компоненты линейных и угловых перемещений
расчётных узлов системы.
Расчётными узлами являются:
1) места соединения двух и более элементов
или точки перелома оси ломаного стержня:
2) точки изменения жёсткости сечения стержня:
EI1 EI2
u
3) опорные узлы с неизвестными компонентами
перемещений:
q
4) дополнительно – любые точки системы:
C S 1 const
C S 2 const
v
q

18.

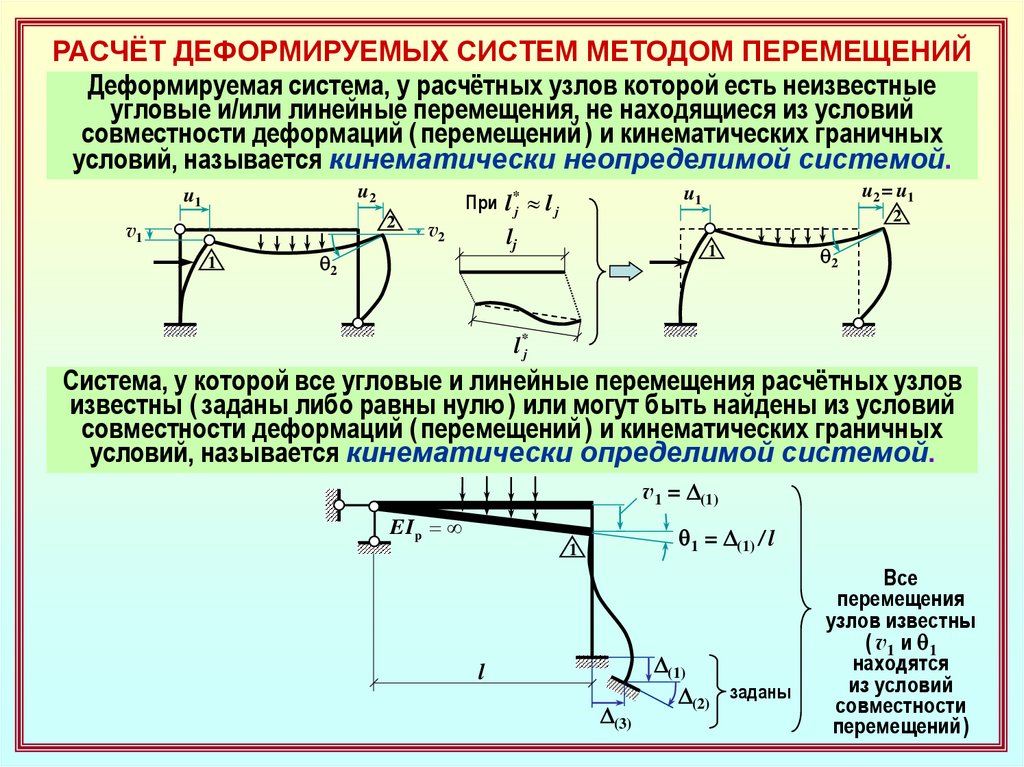
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Деформируемая система, у расчётных узлов которой есть неизвестные
угловые и/или линейные перемещения, не находящиеся из условий
совместности деформаций ( перемещений ) и кинематических граничных
условий, называется кинематически неопределимой системой.
u2
u1
2
v1
1
v2
2
lj
q2
u2 = u1
u1
При l *j l j
1
q2
l *j
Система, у которой все угловые и линейные перемещения расчётных узлов
известны ( заданы либо равны нулю ) или могут быть найдены из условий
совместности деформаций ( перемещений ) и кинематических граничных
условий, называется кинематически определимой системой.
v1 = D(1)
EI p
q1 = D(1) / l
1
l
D(3)
D(1)
D(2) заданы
Все
перемещения
узлов известны
( v1 и q 1
находятся
из условий
совместности
перемещений )

19.

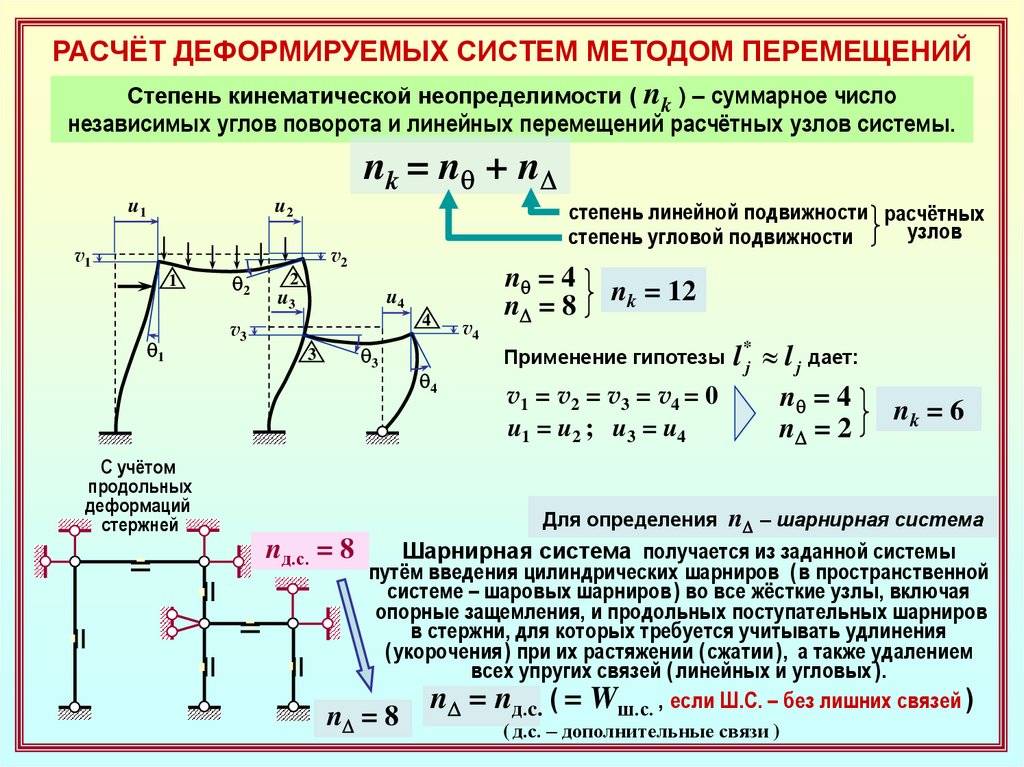
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Степень кинематической неопределимости ( nk ) – суммарное число
независимых углов поворота и линейных перемещений расчётных узлов системы.
nk = n q + nD
u1
u2
степень линейной подвижности расчётных
узлов
степень угловой подвижности
v2
v1
1
q1
q2
2
u4
u3
4
v3
3
q3
q4
v4
nq = 4
nD = 8
nk = 12
Применение гипотезы l j l j дает:
*
v1 = v2 = v3 = v4 = 0
u1 = u2 ; u3 = u4
nq = 4
nD = 2
nk = 6
В nж.у. учитываются неопорные узлы с припайками, а также
узлы ( в т.ч. опорные ) с упругоподатливыми угловым связями.
nж.у. – для плоской системы
nθ
3nж.у.– для пространственной системы
( ж.у. – жёсткие узлы )
nж.у. = 4
nж.у. = 2
Для определения nD – шарнирная система
Шарнирная система получается из заданной системы
путём введения цилиндрических шарниров ( в пространственной
системе – шаровых шарниров ) во все жёсткие узлы, включая
опорные защемления, и продольных поступательных шарниров
в стержни, для которых требуется учитывать удлинения
( укорочения ) при их растяжении ( сжатии ), а также удалением
всех упругих связей ( линейных и угловых ).
nD = nд.c. ( = Wш.с. , если Ш.С. – без лишних связей )
( д.с. – дополнительные связи )

20.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Степень кинематической неопределимости ( nk ) – суммарное число
независимых углов поворота и линейных перемещений расчётных узлов системы.
nk = n q + nD
u1
u2
степень линейной подвижности расчётных
узлов
степень угловой подвижности
v2
v1
1
q1
q2
2
u4
u3
4
v3
3
q3
q4
v4
nq = 4
nD = 8
nk = 12
Применение гипотезы l j l j дает:
*
v1 = v2 = v3 = v4 = 0
u1 = u2 ; u3 = u4
nq = 4
nD = 2
nk = 6
В nж.у. учитываются неопорные узлы с припайками, а также
узлы ( в т.ч. опорные ) с упругоподатливыми угловым связями.
nж.у. – для плоской системы
nθ
3nж.у.– для пространственной системы
При l *j l j
Для определения nD – шарнирная система
Шарнирная система получается из заданной системы
путём
введения цилиндрических шарниров ( в пространственной
nд.с. = 2 системе
– шаровых шарниров ) во все жёсткие узлы, включая
опорные защемления, и продольных поступательных шарниров
в стержни, для которых требуется учитывать удлинения
( укорочения ) при их растяжении ( сжатии ), а также удалением
всех упругих связей ( линейных и угловых ).
nD = nд.c. ( = Wш.с. , если Ш.С. – без лишних связей )
nD = 2
( д.с. – дополнительные связи )

21.

РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Степень кинематической неопределимости ( nk ) – суммарное число
независимых углов поворота и линейных перемещений расчётных узлов системы.
nk = n q + nD
u1
u2
степень линейной подвижности расчётных
узлов
степень угловой подвижности
v2
v1
q2
1
2
u4
u3
4
v3
q1
q3
3
С учётом
продольных
деформаций
стержней
=
=
=
=
nk = 12
Применение гипотезы l j l j дает:
*
v1 = v2 = v3 = v4 = 0
u1 = u2 ; u3 = u4
nq = 4
nD = 2
nk = 6
Для определения nD – шарнирная система
nд.с. = 8
=
=
q4
v4
nq = 4
nD = 8
Шарнирная система получается из заданной системы
путём введения цилиндрических шарниров ( в пространственной
системе – шаровых шарниров ) во все жёсткие узлы, включая
опорные защемления, и продольных поступательных шарниров
в стержни, для которых требуется учитывать удлинения
( укорочения ) при их растяжении ( сжатии ), а также удалением
всех упругих связей ( линейных и угловых ).
nD = nд.c. ( = Wш.с. , если Ш.С. – без лишних связей )
nD = 8
( д.с. – дополнительные связи )

22.

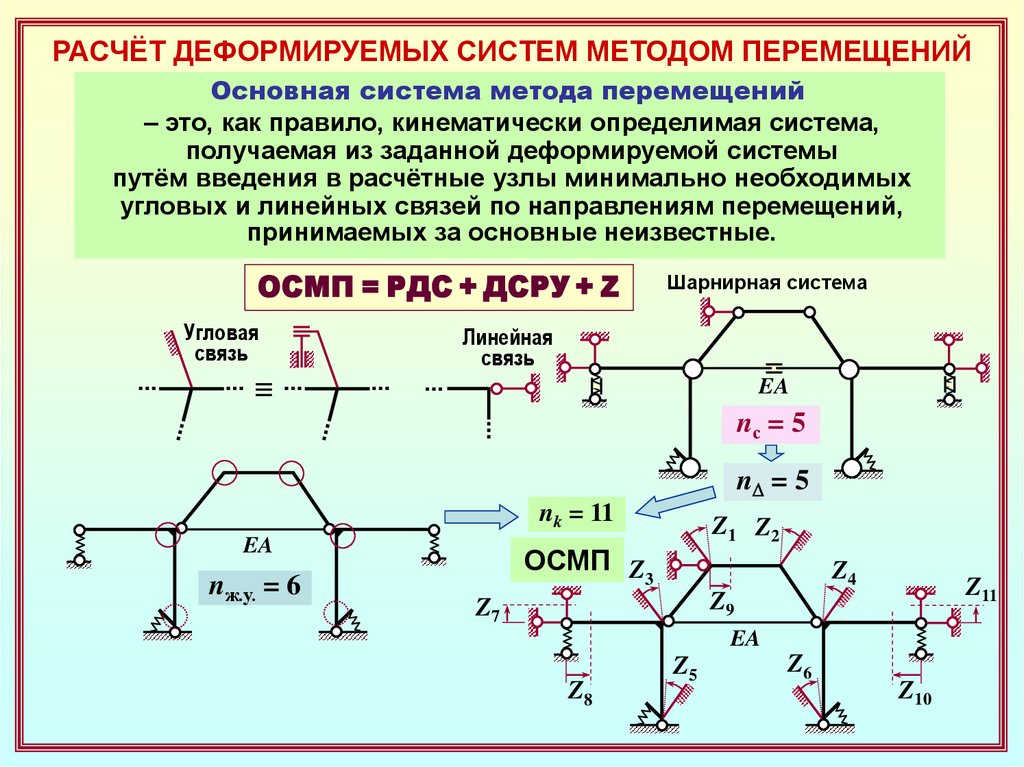
РАСЧЁТ ДЕФОРМИРУЕМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Основная система метода перемещений
– это, как правило, кинематически определимая система,
получаемая из заданной деформируемой системы
путём введения в расчётные узлы минимально необходимых
угловых и линейных связей по направлениям перемещений,
принимаемых за основные неизвестные.
ОСМП = РДC + ДСРУ + Z
Угловая
связь
Шарнирная система
Линейная
связь
EA
nс = 5
nD = 5
nk = 11
EA
nж.у. = 6
Z1 Z 2
ОСМП Z3
Z4
Z11
Z9
Z7
EA
Z8
Z5
Z6
Z10

23.

Контрольные вопросы
( в скобках даны номера слайдов, в которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 23» )
1. Какой метод расчёта деформируемых систем называется методом
перемещений? ( 2 )
2. Что принимается за основные неизвестные в методе перемещений? ( 17 )
Как они обозначаются? ( 22 )
3. Признаки расчетных узлов системы ( 17 ) .
4. Что такое кинематически неопределимая система (КНС)? ( 18 )
5. Какая система называется кинематически определимой? ( 18 )
6. Что такое степень кинематической неопределимости (nк)? ( 19 )
7. Из чего складывается nк? ( 19 )
8. По каким формулам можно вычислять nк для плоских стержневых систем?
Для пространственных систем? Чему равны nq и nD? ( 19 )
9. Что такое шарнирная система, как она получается и для чего используется? ( 19 )
10. Как при формировании шарнирной системы учитываются элементы, удлинениями
которых при растяжении (сжатии) нельзя пренебрегать? ( 19 )
11. Какую рабочую гипотезу вводят в МП для стержней, работающих преимущественно
на изгиб, и каково следствие применения этой гипотезы (влияние на количество
основных неизвестных)? ( 18 ) , ( 20 – 21 )
12. Идея метода перемещений ( 15 – 16 ) . Как вычисляются усилия в концевых сечениях
стержней через их смещения и воздействия, приложенные к данному стержню? ( 7 )
13. Что такое матрица жёсткости стержня? ( 7 ) , ( 11 – 12 )
14. Что такое основная система метода перемещений (ОСМП)? ( 22 )
*) Только в режиме «Показ слайдов».