Похожие презентации:
Устойчивость рам. Расчет рам на устойчивость методом перемещений
1.
1УСТОЙЧИВОСТЬ РАМ
2.
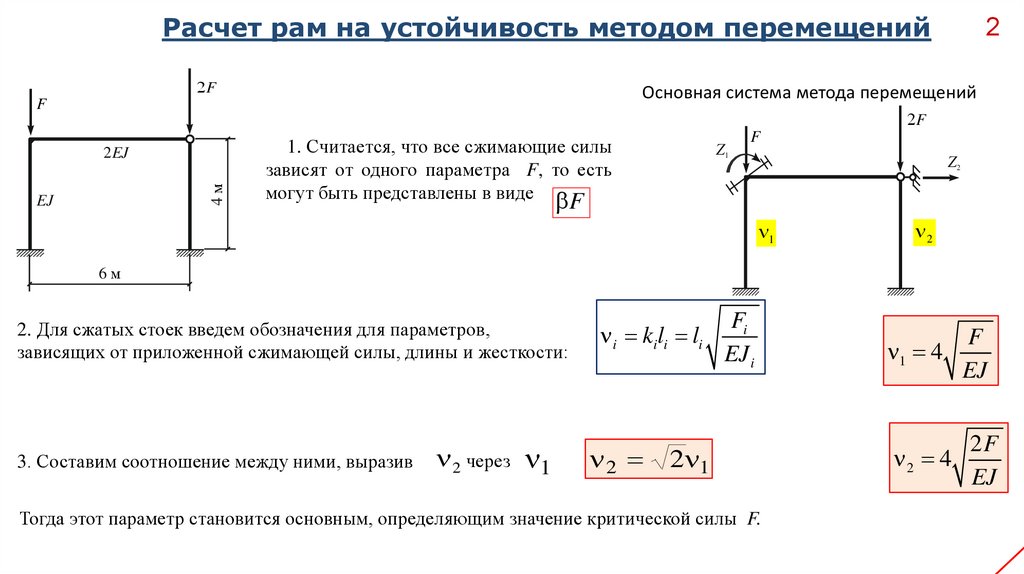
Расчет рам на устойчивость методом перемещенийF
2P
FP
4м
2EJ
EJ
2
Основная система метода перемещений
1. Считается, что все сжимающие силы
зависят от одного параметра F, то есть
могут быть представлены в виде
Z1
FP
F
2P
Z2
F
1
2
6м
2. Для сжатых стоек введем обозначения для параметров,
зависящих от приложенной сжимающей силы, длины и жесткости:
3. Составим соотношение между ними, выразив
2 через 1
i kili li
2
Fi
EJ i
2 1
Тогда этот параметр становится основным, определяющим значение критической силы F.
F
1 4
EJ
2F
2 4
EJ
3.
34. Построим единичные эпюры в основной системе метода перемещений.
При этом для сжатых стоек эпюры будут криволинейными и строятся по «новым» таблицам.
5. Составим систему канонических уравнений метода перемещений
Такая система называется однородной и имеет два решения:
r11Z1 r12 Z 2 0,
r21Z1 r22 Z 2 0.
1. Z1 Z 2 0 − тривиальное решение (отсутствие потери устойчивости),
2. Z1 0,
Z 2 0 − потеря устойчивости.
Но тогда определитель должен быть равен нулю:
det r11r22 r12 r21 r11r22 (r12 ) 2 0
Получаем трансцендентное уравнение, которое решается подбором или в какой-либо среде (Excel)
4.
ПримерZ1
4
FP
r11Z1 0
1. Z1 0
- тривиальное решение (отсутствие потери устойчивости),
2. Z1 0
r11 0 − потеря устойчивости.
5.
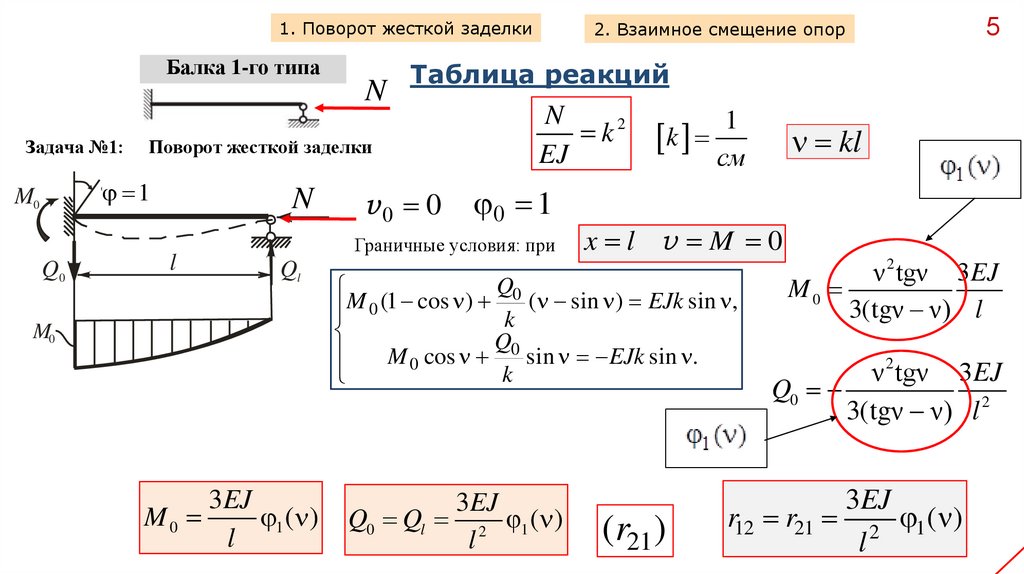
1. Поворот жесткой заделкиБалка 1-го типа
N
Задача №1:
Q0
M0
N
l
v0 0
N
k2
EJ
0 1
Граничные условия: при
Ql
5
Таблица реакций
Поворот жесткой заделки
=1
1
M0
2. Взаимное смещение опор
1
k
см
kl
x l v M 0
Q0
M
(
1
cos
)
( sin ) EJk sin ,
0
k
Q0
M 0 cos
sin EJk sin .
k
ν 2 tgν 3EJ
M0
3(tgν ν) l
ν 2 tgν 3EJ
Q0
3(tgν ν) l 2
6.
1. Поворот жесткой заделкиБалка 1-го типа
N
Задача №1:
Q0
N
l
v0 0
N
k2
EJ
0 1
Граничные условия: при
Ql
M0
3EJ
M0
1 ( )
l
5
Таблица реакций
Поворот жесткой заделки
=1
1
M0
2. Взаимное смещение опор
1
k
см
x l v M 0
Q0
M
(
1
cos
)
( sin ) EJk sin ,
0
k
Q0
M 0 cos
sin EJk sin .
k
3EJ
Q0 Ql 2 1 ( )
l
kl
(r21 )
ν 2 tgν 3EJ
M0
3(tgν ν) l
ν 2 tgν 3EJ
Q0
3(tgν ν) l 2
3EJ
r12 r21 2 1 ( )
l
7.
Таблица реакций6
Балка 1-го типа
N
Задача №2:
M0
Q0
Смещение опоры
l
Ql
M0
N
=1
v 0 0 0 0
N
Граничные условия: при
x l v 1 M 0
Q0
2
M
(
1
cos
)
(
sin
)
EJk
,
0
k
Q
M 0 cos 0 sin 0.
k
ν 2 tgν 3EJ
M0
3(tgν ν) l 2
3
3EJ
Q0
3(tg ) l 3
8.
Таблица реакций6
Балка 1-го типа
N
Задача №2:
M0
Q0
Смещение опоры
l
Ql
M0
3EJ
r12 r21 2 1 ( )
l
3EJ
M 0 2 1 ( )
l
N
=1
v 0 0 0 0
N
Граничные условия: при
x l v 1 M 0
Q0
2
M
(
1
cos
)
(
sin
)
EJk
,
0
k
Q
M 0 cos 0 sin 0.
k
3EJ
Q0 Ql 3 1 ( )
l
ν 2 tgν 3EJ
M0
3(tgν ν) l 2
3
3EJ
Q0
3(tg ) l 3
9.
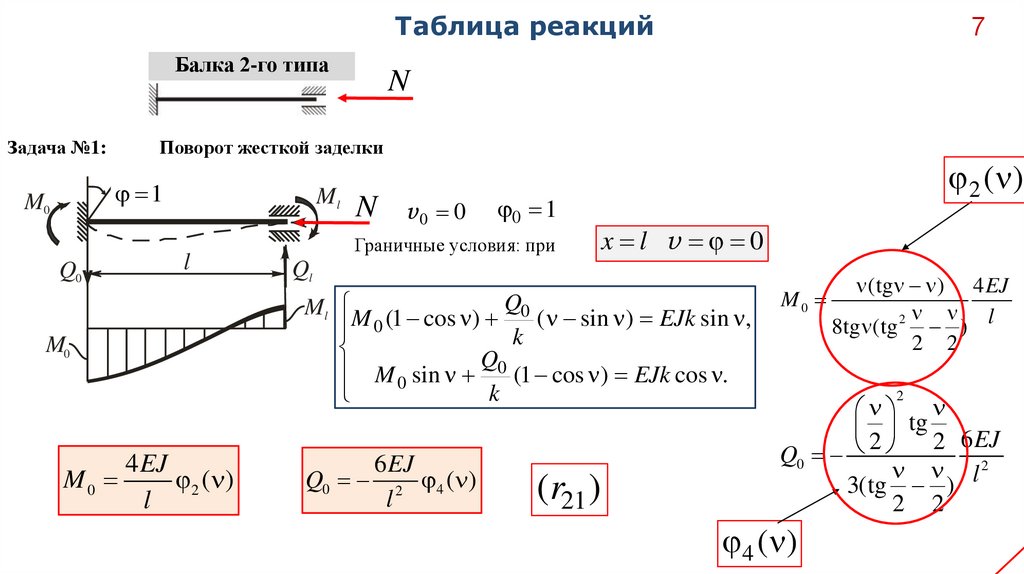
Таблица реакцийБалка 2-го типа
Задача №1:
Q0
M0
N
Поворот жесткой заделки
=1
1
M0
7
Ml
l
N
v0 0
0 1
Граничные условия: при
2 ( )
x l v 0
Ql
Ml
Q0
M 0 (1 cos ) k ( sin ) EJk sin ,
Q
M 0 sin 0 (1 cos ) EJk cos .
k
M0
(tg ) 4 EJ
8tg (tg 2 ) l
2 2
tg
2
2 6 EJ
Q0
l2
3(tg )
2 2
4 ( )
2
10.
Таблица реакцийБалка 2-го типа
Задача №1:
Q0
N
Поворот жесткой заделки
=1
1
M0
7
Ml
l
M0
4 EJ
M0
2 ( )
l
N
v0 0
0 1
Граничные условия: при
2 ( )
x l v 0
Ql
Ml M (1 cos ) Q0 ( sin ) EJk sin ,
0
k
Q
M 0 sin 0 (1 cos ) EJk cos .
k
6 EJ
Q0 2 4 ( )
l
(r21 )
M0
(tg ) 4 EJ
8tg (tg 2 ) l
2 2
tg
2
2 6 EJ
Q0
l2
3(tg )
2 2
4 ( )
2
11.
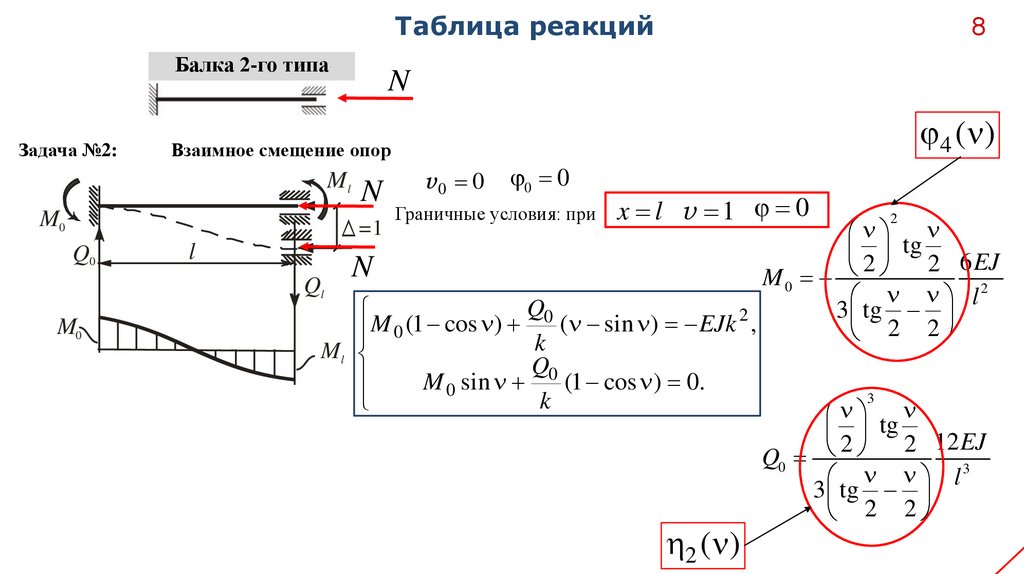
Таблица реакцийБалка 2-го типа
Задача №2:
N
M0
N
M0
l
v0 0
0 0
Граничные условия: при
x l v 1 0
tg
2
2 6 EJ
N
M0
Ql
l2
Q0
3 tg
2
M
(
1
cos
)
(
sin
)
EJk
,
2 2
0
k
Ml
Q0
M 0 sin
(1 cos ) 0.
3
k
tg 12 EJ
2
2
Q0
l3
3 tg
2 2
=1
Q0
4 ( )
Взаимное смещение опор
Ml
8
2 ( )
2
12.
Таблица реакцийБалка 2-го типа
Задача №2:
M0
N
4 ( )
Взаимное смещение опор
Ml
8
N
v0 0
0 0
Граничные условия: при
x l v 1 0
tg
l
Q0
2
2 6 EJ
N
M0
Ql
l2
Q0
3 tg
2
M
(
1
cos
)
(
sin
)
EJk
,
M0
2 2
0
k
Ml
Q0
M 0 sin
(1 cos ) 0.
3
k
6 EJ
r12 r21 2 4 ( )
tg 12 EJ
2
2
l
Q0
l3
3 tg
2 2
6 EJ
12 EJ
M 0 2 4 ( )
Q0 3 2 ( )
2 ( )
l
l
=1
2
13.
Таблица реакций9
Статически определимые балки
1. Консольная балка
Поворот жесткой заделки
=1
1
M0
M0
N
l
N
v0 0
0 1 Q0 0
Граничное условие: при
x l M 0
M (l ) EJk sin M 0 cos
EJk sin
EJkl
EJ
M0
tg
tg
cos
l
l
5 ( )
EJ
M0
5 ( )
l
14.
Таблица реакций9
Статически определимые балки
1. Консольная балка
Поворот жесткой заделки
=1
1
M0
N
l
N
v0 0
0 1 Q0 0
Граничное условие: при
x l M 0
M (l ) EJk sin M 0 cos
EJk sin
EJkl
EJ
M0
tg
tg
cos
l
l
M0
5 ( )
EJ
M0
5 ( )
l
2. Балка на двух шарнирных опорах
Смещение опоры
N
A
Q0
M N 1 Q l 0
A
=1
l
N
Ql
l
N k 2 EJ
N k 2 EJ k 2l 2 EJ 2 EJ
Ql
3
3
l
l
l
l
EJ 2
Ql Q0 3
l
15.
1016.
1117.
1218.
1319.
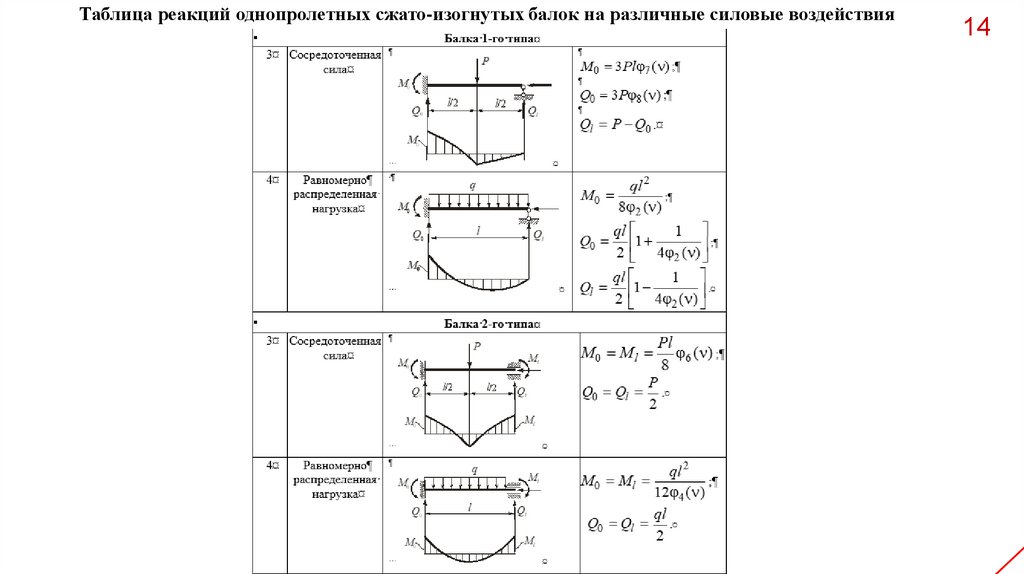
Таблица реакций однопролетных сжато-изогнутых балок на различные силовые воздействия14
20.
Таблица реакций однопролетных сжато-изогнутых балок на различные силовые воздействияP
Ml
v 0 0 0 0
Ml
при
M0
Q0
M0
l/2
l/2
Ql
l
x
2
P
Q0
2
0
M 0 sin
Q0
1 cos 0
2 k
2
15
21.
Таблица реакций однопролетных сжато-изогнутых балок на различные силовые воздействияP
Ml
v 0 0 0 0
Ml
при
M0
Q0
l/2
M0
l/2
Ql
l
x
2
P
Q0
2
0
M 0 sin
Q0
1 cos 0
2 k
2
2
2sin
4tg
Pl
Pl
Pl
2
4
4
M0
6 ( )
2k sin
2 2sin cos
8
8
2
4
4
P 1 cos
kl
l
k
4 tg
4
6 ( )
15
22.
Таблица реакций однопролетных сжато-изогнутых балок на различные силовые воздействияq
Ml
M0
Q0
M0
l
Ql
ql
Q0
2
v 0 0 0 0
при
l
x
2
16
0
Ml
M 0 sin
Q0
q
1 cos
sin
0
2 k
2 kN 2
2
23.
Таблица реакций однопролетных сжато-изогнутых балок на различные силовые воздействияq
Ml
M0
Q0
l
Ql
Ml
M0
v 0 0 0 0
при
l
x
2
ql
Q0
2
0
Q0
q
M 0 sin 1 cos
sin 0
2 k
2 kN 2
2
2
sin
2sin
2
2
2
q
ql
ql
1
1
ql
2
2
2
4
M0
2
2k sin
k
2 2sin cos
4sin cos
12 4 (
sin
2
2
4
4
4
4
ql 1 cos
3(tg )
1
2 2
4 ( 2
tg
2
2
16
24.
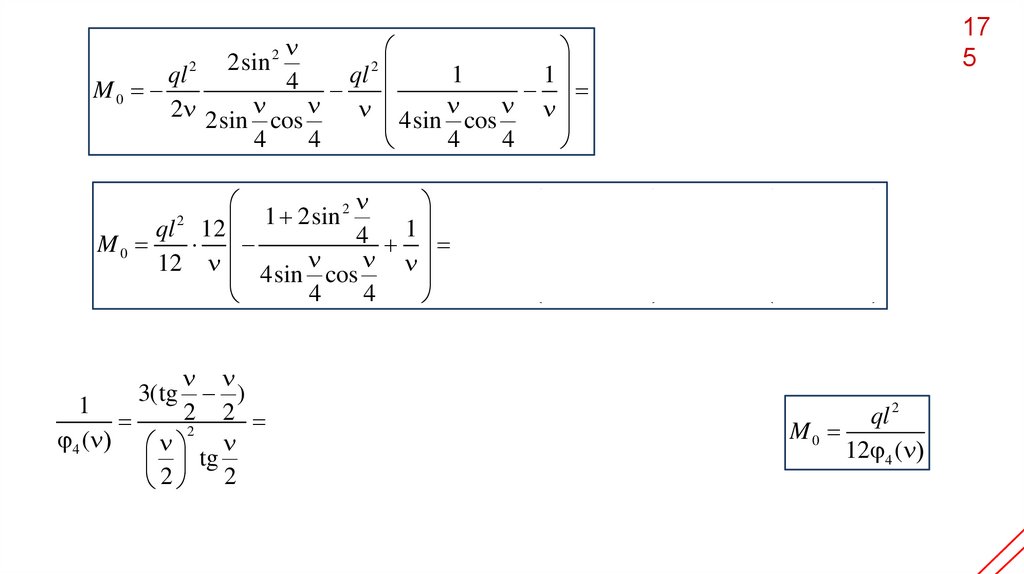
175
4
ql 2
ql 2
1
1
M0
2 2sin cos
4sin cos
4
4
4
4
2sin 2
2
1
2sin
cos
2
2
ql 2 12
1
ql
12
1
ql
12 1
1
4
2
M0
12 4sin cos
12 2sin 12 2tg
4
4
2
2
3
3(tg
)
3tg
1
12
12
12 1
1
2
2
2
2
2
2
2
4 (
tg
tg
tg
tg
2
2
2
2
2
2
ql 2
M0
12 4 (


















 Механика
Механика








