Воздействие сигналов на нелинейные элементы. (Тема 3)

1. Теория Информационных Процессов

Тема №3: Воздействие
сигналов на нелинейные
элементы

2. План

Преобразования сигналов
Классы нелинейных элементов
Режимы работы нелинейного элемента
Методы аппроксимации
Воздействие сигналов различных видов
на нелинейных элемент

3. Преобразования сигналов

Основные преобразования сигналов
осуществляются с помощью:
Нелинейных электрических цепей
Линейных цепей с переменными параметрами
Необходим нелинейный элемент!
Пример: емкость p-n перехода в полупроводниковом диоде

4. Классы нелинейных элементов

Резистивные (сопротивления)
Реактивные (индуктивность, емкость)
Пример резистивного элемента: полупроводниковые,
ламповые и другие приборы, имеющие нелинейную вольтамперную характеристику

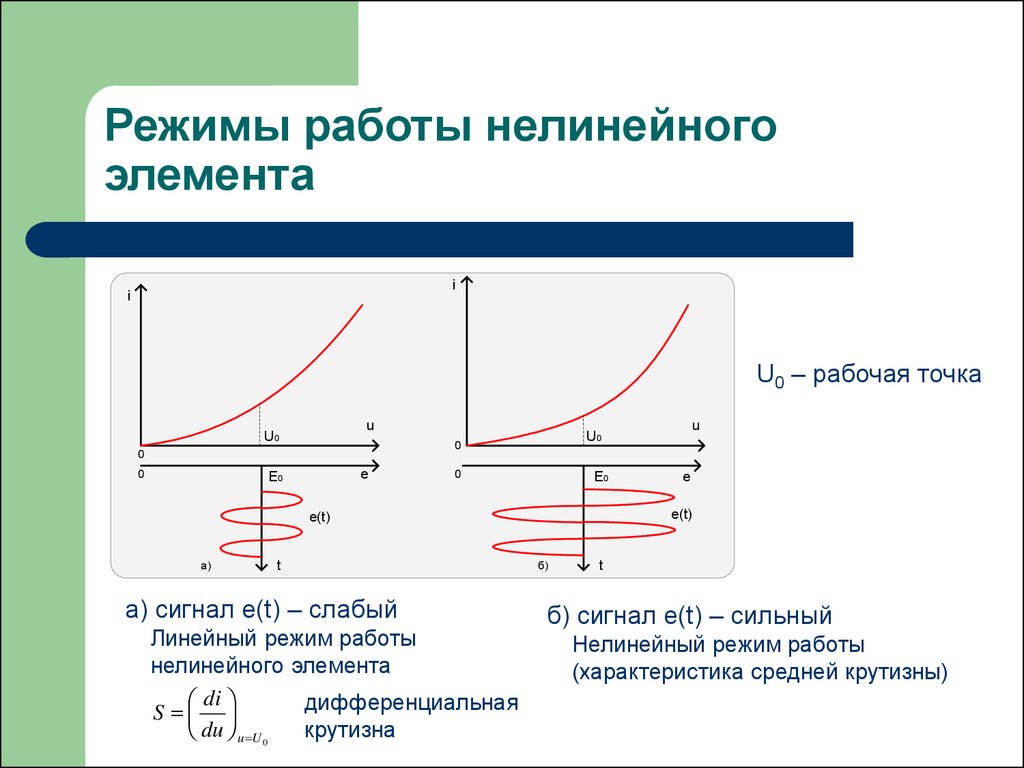
5. Режимы работы нелинейного элемента

i
i
U0 – рабочая точка
u
U0
0
0
e
E0
0
E0
t
а) сигнал e(t) – слабый
Линейный режим работы
нелинейного элемента
di
дифференциальная
S
крутизна
du u U 0
e
e(t)
e(t)
а)
u
U0
0
б)
t
б) сигнал e(t) – сильный
Нелинейный режим работы
(характеристика средней крутизны)

6. Примеры

Пример нелинейной емкости:
Устройство с нелинейной вольткулоновской
характеристикой q(u)
Устройство с нелинейной вольтфарадной
характеристикой c(u)=q(u)/u
Пример нелинейной индуктивности L(i):
Катушка с ферромагнитным сердечником,
обтекаемым сильным током

7. Метод аппроксимации

Для анализа нелинейных цепей необходимо
задать вольтамперные или иные аналогичные
характеристики
Широкое распространение получил способ
представления характеристики методом
аппроксимации
Оптимальный выбор способа аппроксимации
зависит от вида нелинейной характеристики и
от режима работы нелинейного элемента

8. Метод аппроксимации

Аппроксимация системным полиномом:
i (u ) i (U 0 ) a1 (u U 0 ) a2 (u U 0 ) 2 a3 (u U 0 )3 ...
Коэффициенты a1, a2,…
di
a1
du u U 0
1 d 2i
a12 2
2! du u U
0
a1, a2, a3 … существенно зависят от U0 – рабочей точки

9. Воздействие узкополосного сигнала на безинерционный нелинейный элемент

Н.Э. используются в диапазоне частот, на
которых можно пренебречь влиянием паразитных
индуктивностей и емкостей
Рассмотрим режим работы, при котором вольтамперная
характеристика i(u) удовлетворительно аппроксимируется
степенным полиномом
Сигнал e(t) зададим в форме гармонического колебания
e(t ) E cos( 1t 1 ) E cos 1 (t )

10. Воздействие узкополосного сигнала на безинерционный нелинейный элемент

Подставив в ряд разложение e(t)=u-U0 получим
1
3
2
i (t ) i (U 0 ) a2 E a4 E 4 ...
2
8
3
5
a1 E a3 E 3 a5 E 5 ... cos 1 (t )
4
8
1
1
a2 E 2 a4 E 4 ... cos 2 1 (t )
2
2
5
1
a3 E 3 a5 E 5 ... cos 3 1 (t ) ....
16
4
I 0 I1 cos 1 (t ) I 2 cos 2 1 (t ) ...
Здесь используется:
1 1
cos 2 x
2 2
3
1
cos 3 x cos x cos 3 x
4
4
3 1
1
cos 4 x cos 2 x cos 4 x
8 2
8
5
5
1
cos 5 x cos x cos 3x cos 5 x
8
16
16
и т.д.
cos 2 x

11. Воздействие АМ-сигнала на Н.Э.

Для АМ-колебания, когда E=E(t) - нелинейность,
характеристики может коренным образом
исказить форму передаваемого сигнала

12. Воздействие сигнала со сложным спектром

Рассмотрим воздействие суммы гармонических сигналов на
Н.Э.
e(t ) E1 cos( 1t 1 ) E2 cos( 2t 2 )
Пусть
E1 cos 1 (t ) E2 cos 2 (t )
a1e(t ) a1E1 cos 1 (t ) a2 E2 cos 2 (t )
a2 e 2 (t ) a2 [ E1 cos 1 (t ) a2 E2 cos 2 (t )]2
1
1
a2 ( E12 E22 ) a2 E12 cos 2( 1t 1 )
2
2
1
a2 E22 cos 2( 2t 2 ) a2 E1 E2 cos ( 1 2 )t ( 1 2 )
2
a2 E1 E2 cos ( 1 2 )t ( 1 2 )
a3e3 (t ) ...

13. Воздействие сигналов с сложным спектром

Образуются частоты:
m 1 n 2
m n k
Из полученного выражения видны следующие проявления
нелинейности в/а характеристики:
• Постоянный ток получает приращение
1
3
I 0 i (U 0 ) a2 E 2 a4 E 4 ...
2
8
• Амплитуда основной частоты зависит от E
3
I1 a1 E a3 E 2 ...
4
• Ток содержит высшие гармоники
Наивысший порядок гармоники совпадает со
степенью k полинома
Полная фаза n-й гармоники - n (t ) n 1t n 1

14. Воздействие ЧМ-сигнала на Н.Э.

При 1 (t ) 1max s(t ) - модулированная фаза
все полученные выражения сохраняют свой
вид
Итак, при воздействии ЧМ-сигнала на
безинерционный Н.Э. все сформулированные
выше положения сохраняются
In необходимо трактовать как несущее
колебание, модулированное по углу

15. Воздействие ЧМ-сигнала на Н.Э.

Для первой (основной) гармоники индекс угловой
модуляции совпадает с imax=m
Для высших гармоник n imax=nm1
соответственно в n раз увеличивается и
девиация частоты.

16. Воздействие ЧМ-сигнала на Н.Э.

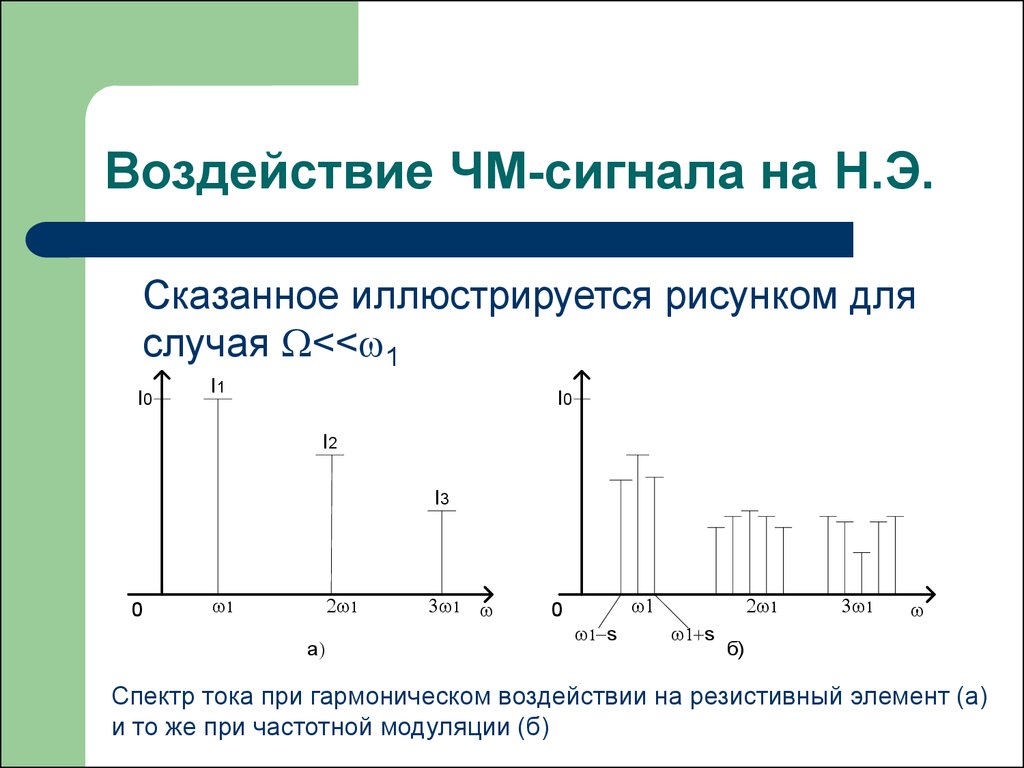
Сказанное иллюстрируется рисунком для
случая << 1
I0
I1
I0
I2
I3
0
1
2 1
а)
3 1
1
0
1 s
2 1
1 s
3 1
б)
Спектр тока при гармоническом воздействии на резистивный элемент (а)
и то же при частотной модуляции (б)

17. Воздействие сложного сигнала.

За счет квадратного члена в/а характеристики k=2
m и n могут принимать следующие значения
m 0, n 0
0
m 2, n 0
2 1
m 0, n 2
2 2
m 1, n 1
1 2
Гармоники 2-го порядка
Комбинационные
частоты 2-го порядка

18. Воздействие сложного сигнала.

За счет кубичного члена a3e3 (t ) в спектре тока
появляются частоты m 1 n 2 со следующими m и n
m 1, n 0
1
m 0, n 1
2
Гармоники 1-го порядка
m 3, n 0
3 1
m 0, n 3
3 2
m 1, n 2
1 2 2
m 2, n 1
2 1 2
Гармоники 3-го порядка
Комбинационные частоты
3-го порядка
Полученные результаты могут быть обобщены на случай
воздействия большого числа гармонических составляющих
на Н.Э.