Похожие презентации:
Переходные процессы в линейных электрических цепях
1. 3. Переходные процессы в линейных электрических цепях
2.
• Переходный процесс – режимработы электрической цепи,
возникающий при переходе цепи
из одного установившегося
состояния в другое установившееся
состояние
• Коммутация – любое изменение
параметров цепей, приводящее к
возникновению переходных
процессов
3.
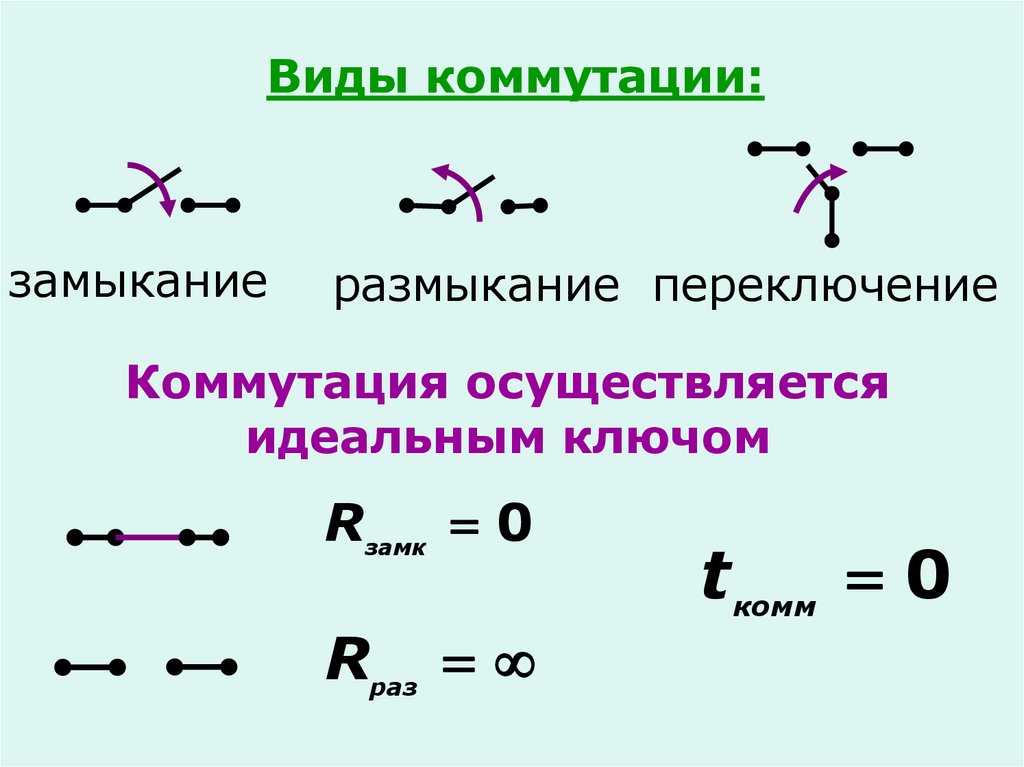
Виды коммутации:замыкание
размыкание переключение
Коммутация осуществляется
идеальным ключом
Rзамк 0
Rраз
t комм 0
4.
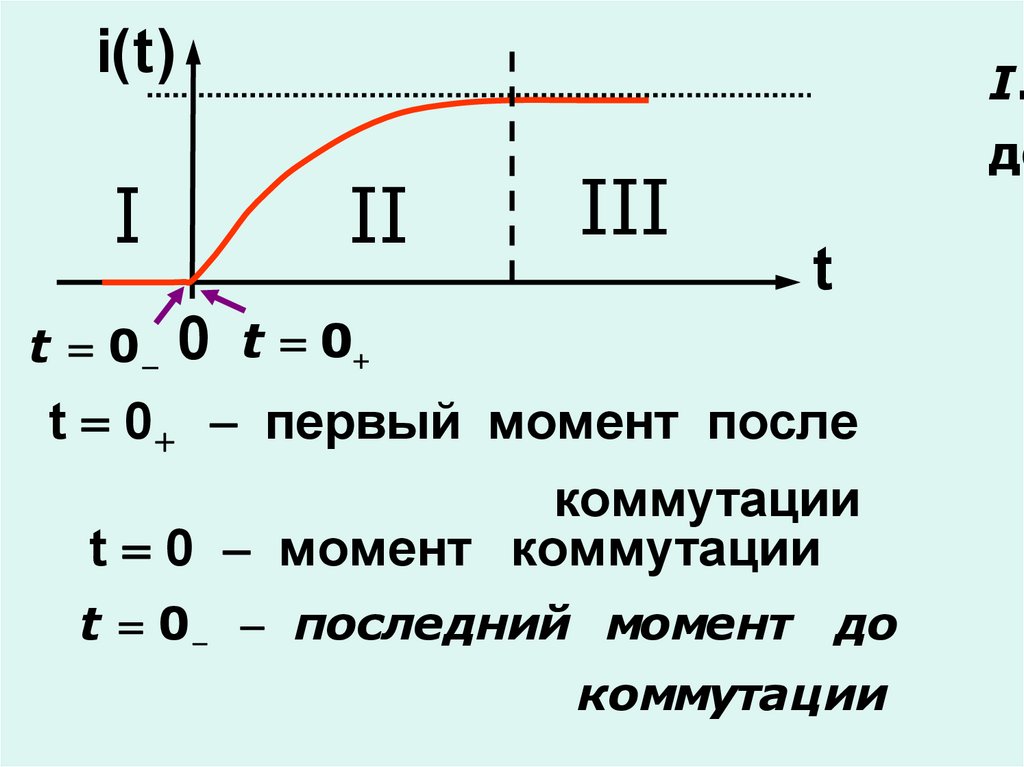
i(t )I
II
III
I.
до
t
t 0 0 t 0
t 0 первый момент после
коммутации
t 0 момент коммутации
t 0 последний момент до
коммутации
5.
Переходный процессвозможен в цепях,
содержащих реактивные
элементы
6. Законы коммутации
1-ый закон Ток в индуктивностине может измениться скачком
iL (0 ) iL (0 )
2-ой закон Напряжение на ёмкости
не может измениться скачком
uC (0 ) uC (0 )
7. Начальные условия - значения токов и напряжений в момент t=0+
Начальные условия значения токов и напряжений вмомент t=0+
Независимые начальные условия – не
изменяются в момент коммутации – ННУ
iL 0 , uC 0
Определяют из схемы до коммутации
t 0
могут быть нулевыми и ненулевыми
8.
Зависимые начальные условия –могутизменяться в момент коммутации –ЗНУ
iC 0 , uL 0 , iR 0 , uR 0
Определяют по законам Кирхгофа из
схемы после коммутации
t 0
9. Расчет переходных процессов первого порядка классическим методом
1. Задать направления токов2. Определить начальные условия
а) ННУ при t 0
б) ЗНУ при t 0
3. Определить при t
принужденную составляющую x пр
10.
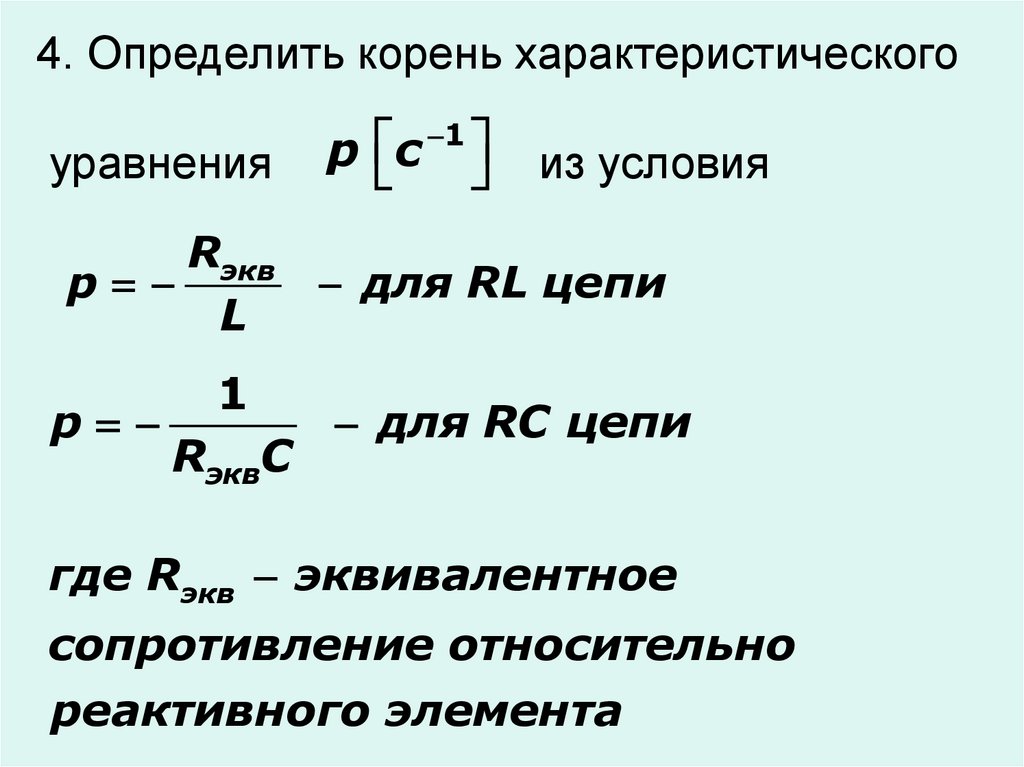
4. Определить корень характеристическогоуравнения
1
p c
из условия
Rэкв
p
для RL цепи
L
p
1
RэквC
для RC цепи
где Rэкв эквивалентное
сопротивление относительно
реактивного элемента
11.
pt5. Для
x(t) xпр A e
используя начальные условия,
определить неизвестный
коэффициент А
6. Построить график
Длительность переходного процесса
tпп 3 5
где
1
p
c
12.
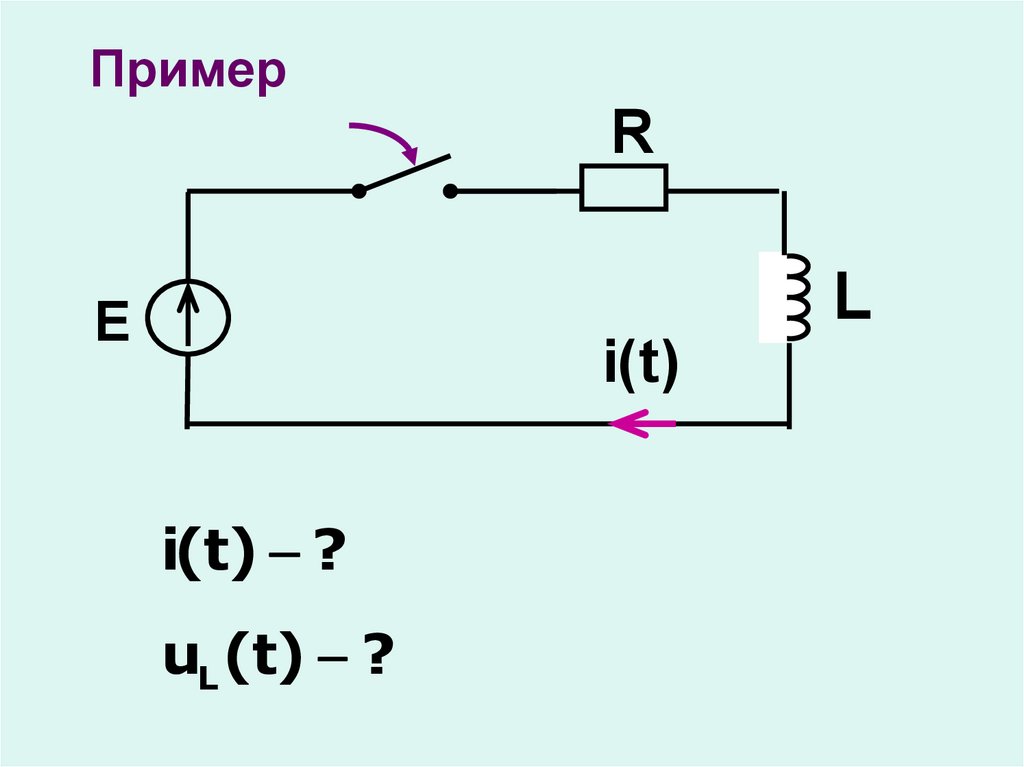
ПримерR
L
E
i(t)
i(t) ?
uL (t) ?
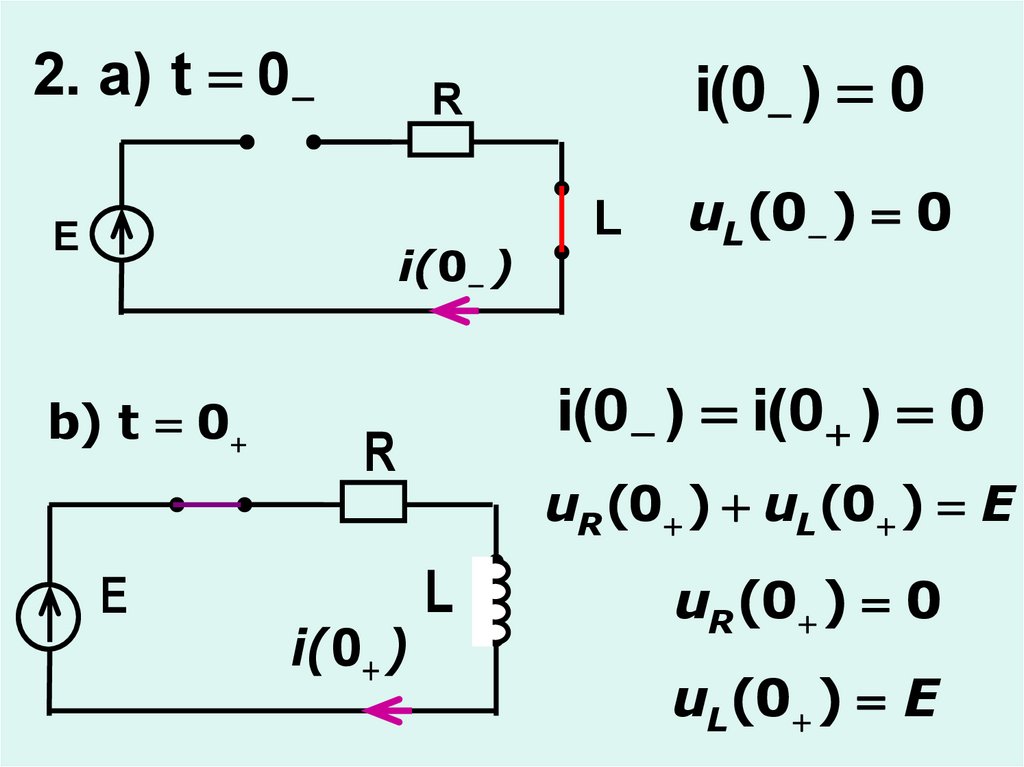
13.
2. a) t 0E
i( 0 )
b) t 0
E
i(0 ) 0
R
uL(0 ) 0
i(0 ) i(0 ) 0
R
i( 0 )
L
uR (0 ) uL(0 ) E
L
uR (0 ) 0
uL(0 ) E
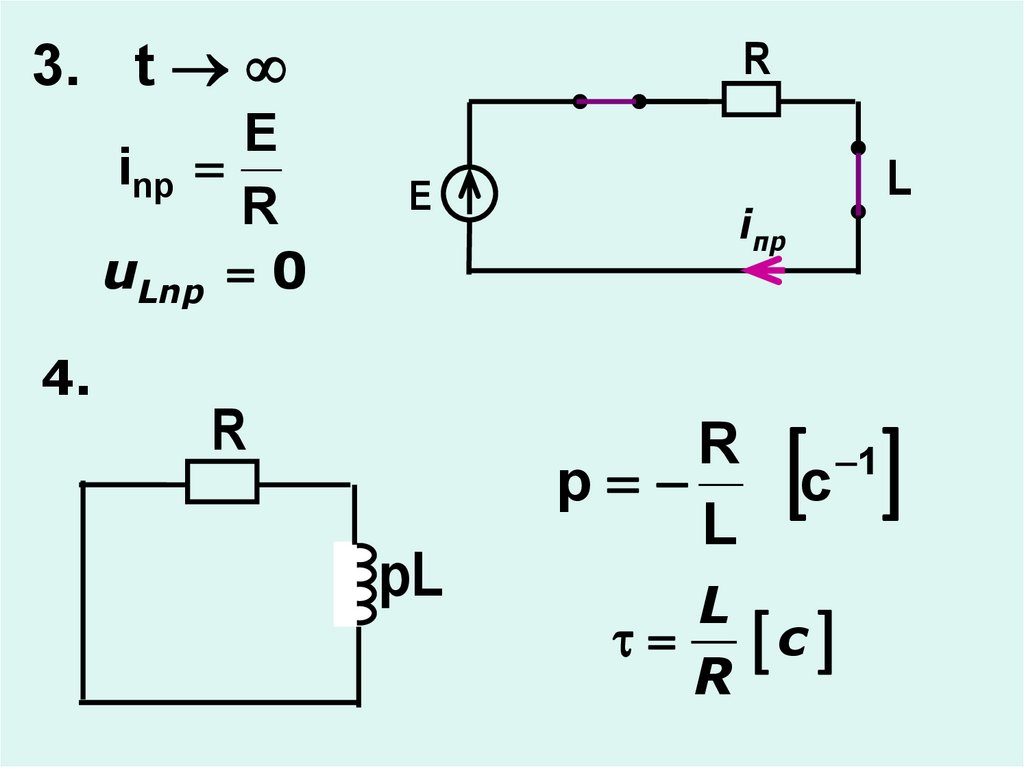
14.
3. tE
inp
R
uLnp 0
R
E
iпр
4.
R
pL
L
R
p
L
c
L
c
R
1
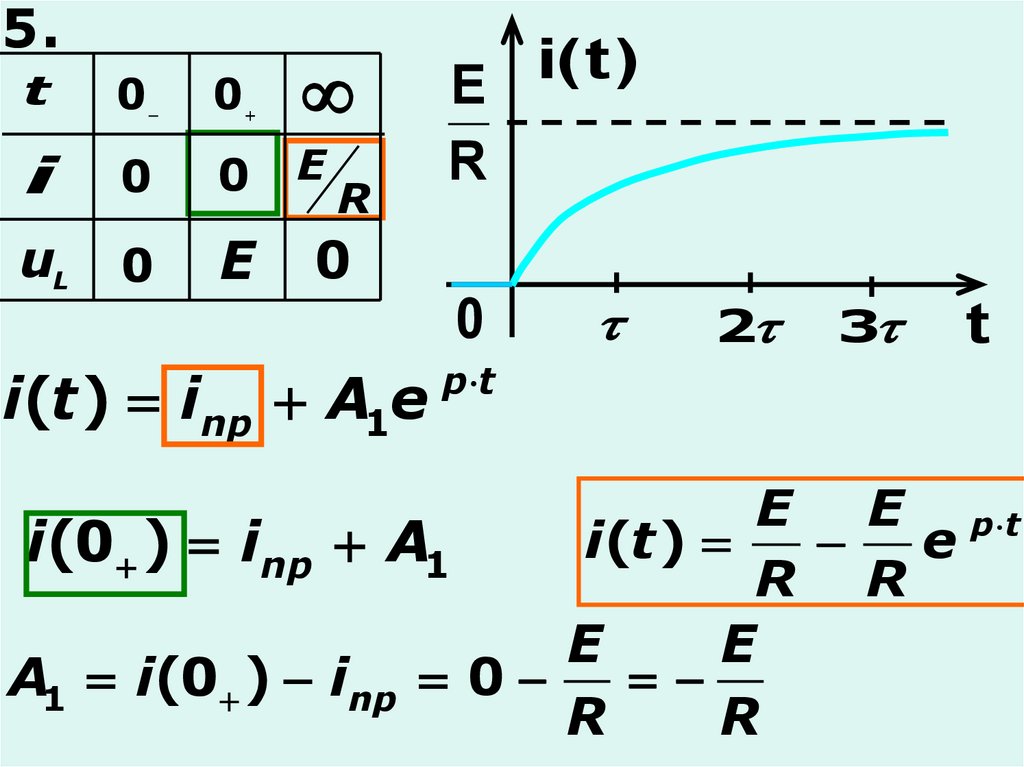
15.
5.t
0
0
i
0
0
E
uL
0
E
0
R
i
(
t
)
E
R
0
i(t ) inp A1e
2
3
t
р t
E E р t
i(t )
e
i(0 ) inp A1
R R
E
E
A1 i(0 ) inp 0
R
R
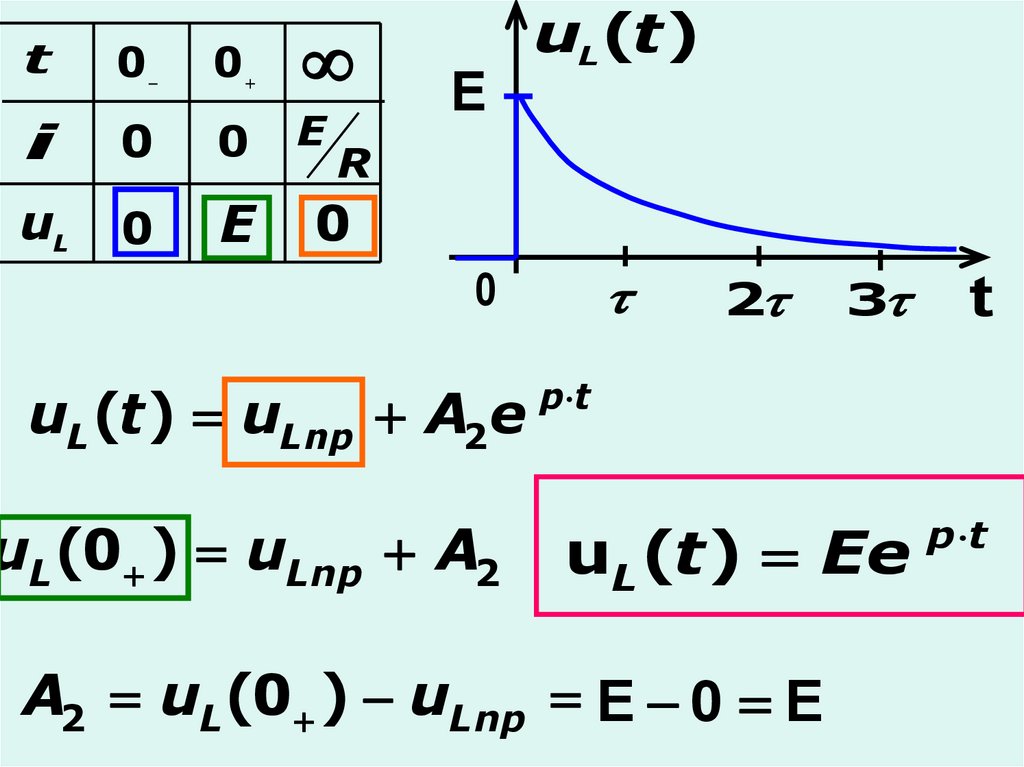
16.
t0
0
i
0
0
E
uL
0
E
0
uL (t )
E
R
uL (t ) uLnp A2 e
uL (0 ) uLnp A2
2
3
t
uL (t ) Ee
р t
0
р t
A2 uL (0 ) uLnp E 0 E
17.
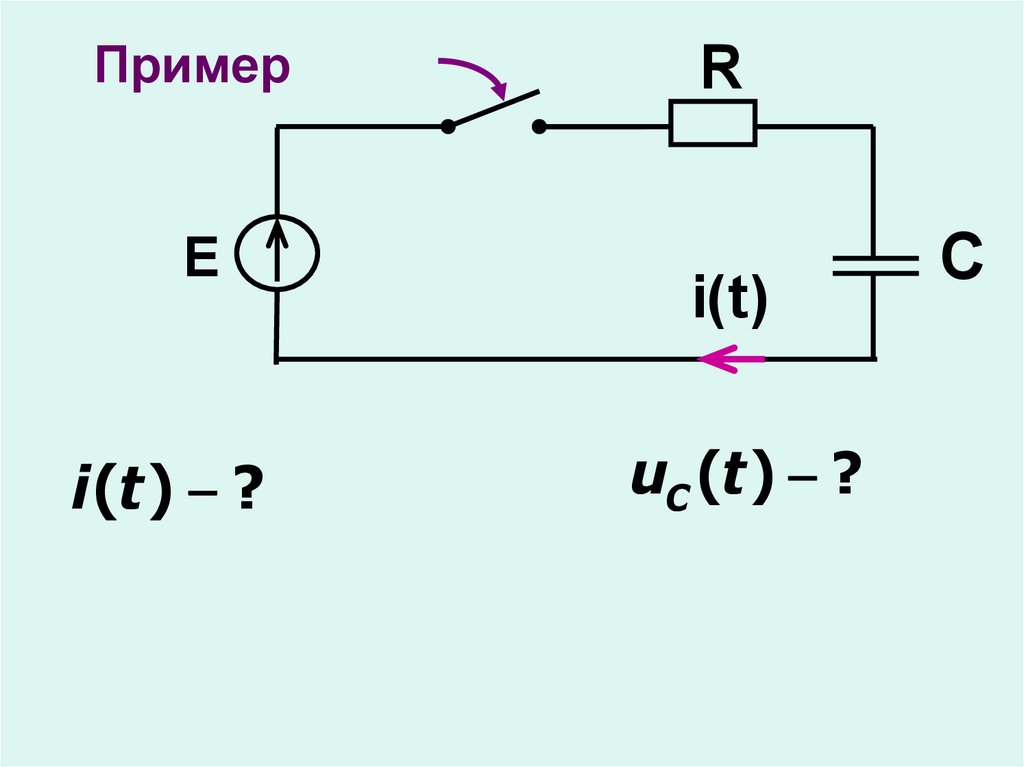
ПримерE
i(t ) ?
R
i(t)
uC (t) ?
C
18.
R2. a) t 0
i(0 ) 0
E
uC (0 ) 0
b) t 0
i( 0 _ )
uR (0 ) uС (0 ) E
R
E
C
uC (0 ) uC (0 ) 0
C
i(0 )
uR (0 ) E
E
i(0 )
R
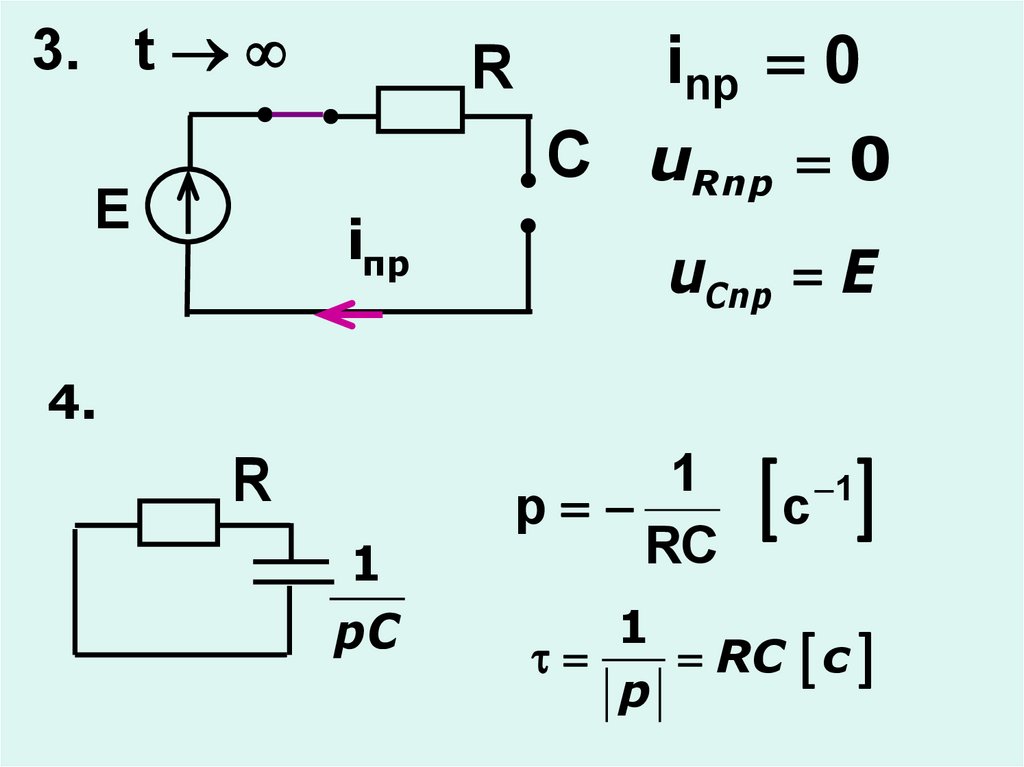
19.
3. tR
inp 0
C uRnp 0
E
iпр
uCnp E
4.
R
1
pC
1
p
RC
c
1
1
RC c
p
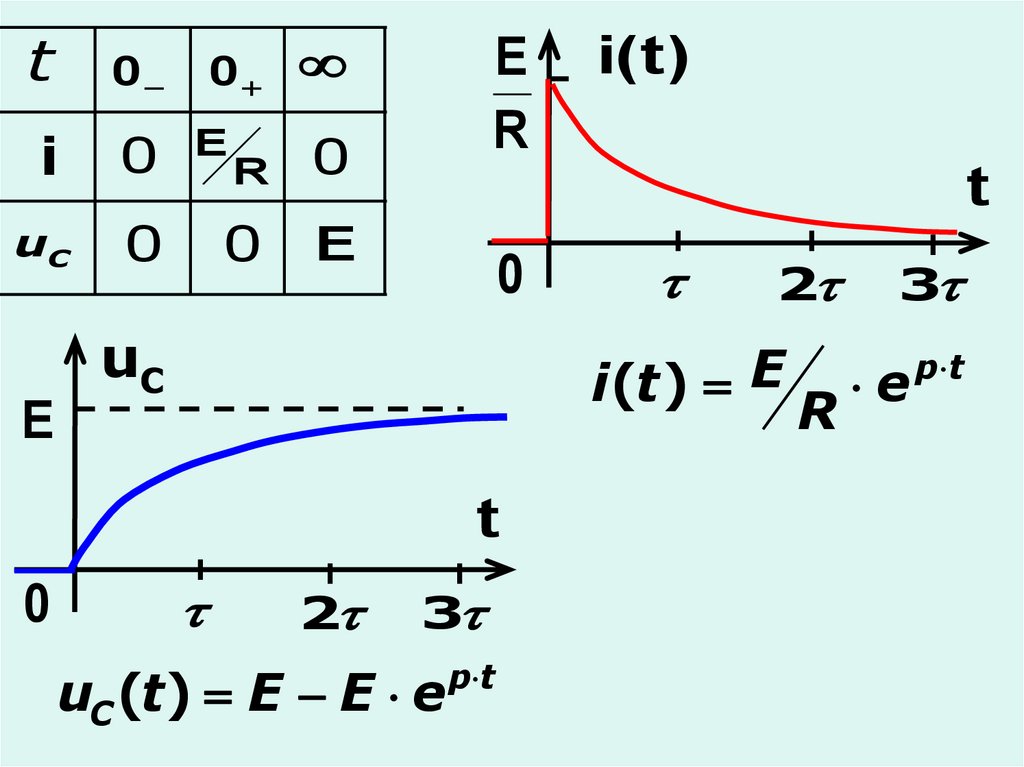
20.
t0
0
i
0
E
R
0
uC
0
0
E
E
R
t
0
uC
2
i(t ) E
E
t
0
i( t )
2
3
uC (t) Е Е e
p t
R
3
e
p t








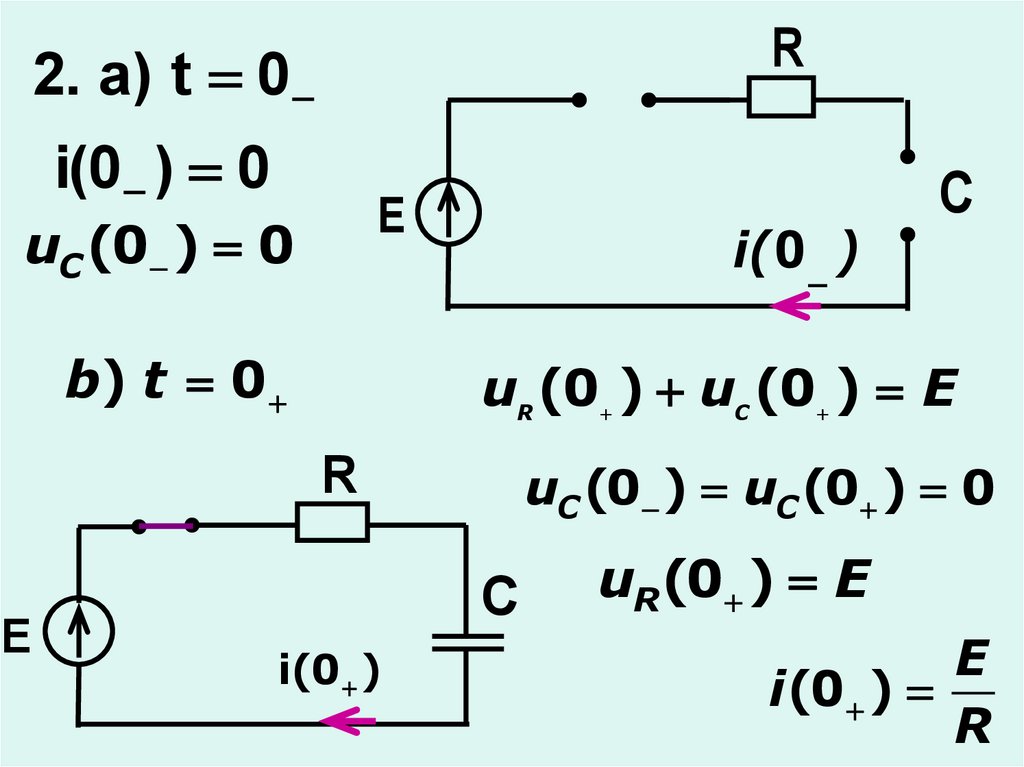
 Физика
Физика








