Схемотехника ЭВМ

1.

СХЕМОТЕХНИКА
ЭВМ
Лектор: профессор
Райхлин Вадим Абрамович
1

2.

ЦЕЛЬ И ЗАДАЧИ ДИСЦИПЛИНЫ
– Cоздание у будущих бакалавров устойчивых представлений об особенностях организации и использования ряда цифровых функциональных узлов, микроcхем и модулей памяти, о способах проектирования цифровых схем в интегральном базисе с учетом динамики протекающих в них процессов.
Задачи дисциплины:
– Освоение схемотехнических принципов организации и использования
микросхем АЛУ, дешифраторов и генераторов импульсов, отечественных микросхем памяти и модулей памяти достаточных объемов.
– Изучение методов анализа переходных процессов в цифровых схемах на
логико-структурном уровне и борьбы с помехами в цепях питания и линиях связи.
– Углубление знаний по вопросам как абстрактного (с элементами интерактивной автоматизации), так и стуктурного (с исключением состязаний) синтеза комбинационных и последовательностных схем.
– Знакомство с методами модульной реализации цифровых схем.
– Приобретение навыков проектирования цифровых устройств по заданному функционированию с учетом динамики.
2

3.

МЕСТО ДИСЦИПЛИНЫ В УЧЕБНОМ ПРОЦЕССЕ
Дисциплина «Схемотехника ЭВМ» входит в вариативную часть
профессионального цикла образовательной программы бакалавра.
Материал курса основан на знаниях, навыках и умениях, почерпнутых студентами из курсов «Теория автоматов», «Электронные вычислительные машины», «Схемотехника».
Студенты должны быть знакомы с архитектурой ЭВМ («Электронные вычислительные машины»), основами теории автоматов
(«Теория автоматов»), базовыми цифровыми микросхемами ТТЛ и
КМОП («Схемотехника»); должны иметь практические навыки преобразования булевых функций и логического синтеза основных цифровых операционных узлов («Теория автоматов»), анализа процессов
в линиях передачи импульсов и базовых цифровых микросхемах
ТТЛ и КМОП («Схемотехника»).
Полученные при изучении дисциплины знания, умения и навыки
будут использованы студентами при изучения дисциплин «Микропроцессорные системы»,«Сети и телекоммуникации»,«Параллельные
вычисления» и при подготовке выпускной работы бакалавра.3

4.

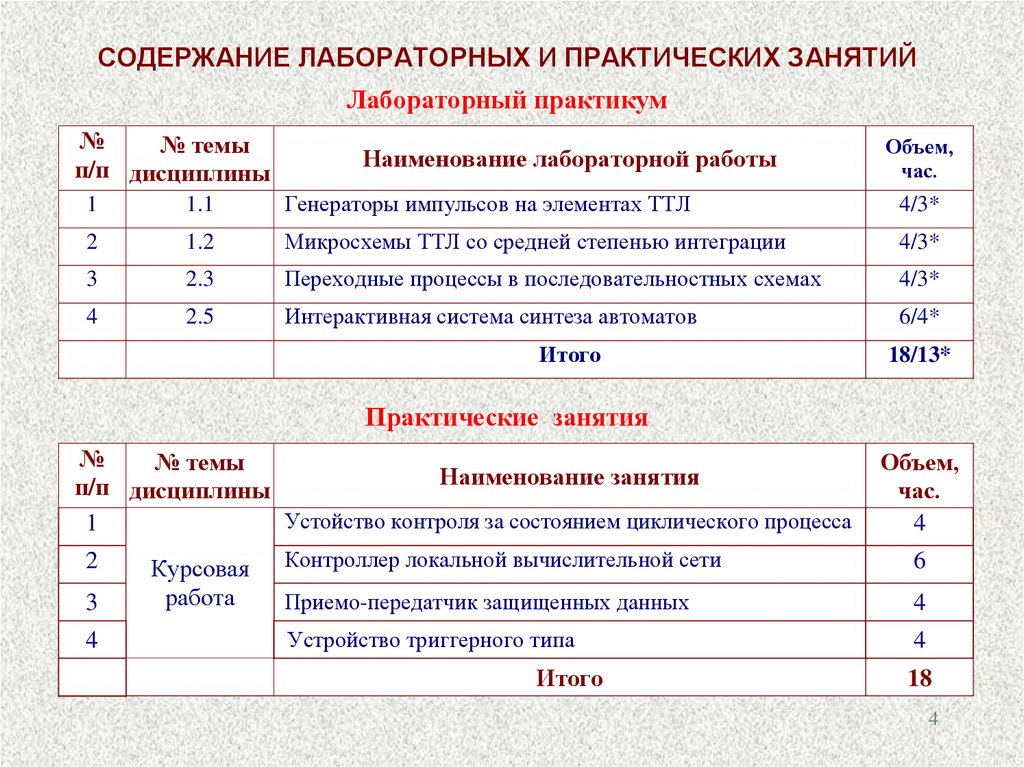
СОДЕРЖАНИЕ ЛАБОРАТОРНЫХ И ПРАКТИЧЕСКИХ ЗАНЯТИЙ
Лабораторный практикум
№
№ темы
п/п дисциплины
Наименование лабораторной работы
Объем,
час.
1
1.1
Генераторы импульсов на элементах ТТЛ
4/3*
2
1.2
Микросхемы ТТЛ со средней степенью интеграции
4/3*
3
2.3
Переходные процессы в последовательностных схемах
4/3*
4
2.5
Интерактивная система синтеза автоматов
6/4*
Итого
18/13*
Практические занятия
№
№ темы
Наименование занятия
п/п дисциплины
Устойство контроля за состоянием циклического процесса
1
2
3
4
Курсовая
работа
Объем,
час.
4
Контроллер локальной вычислительной сети
6
Приемо-передатчик защищенных данных
4
Устройство триггерного типа
4
Итого
18
4

5.

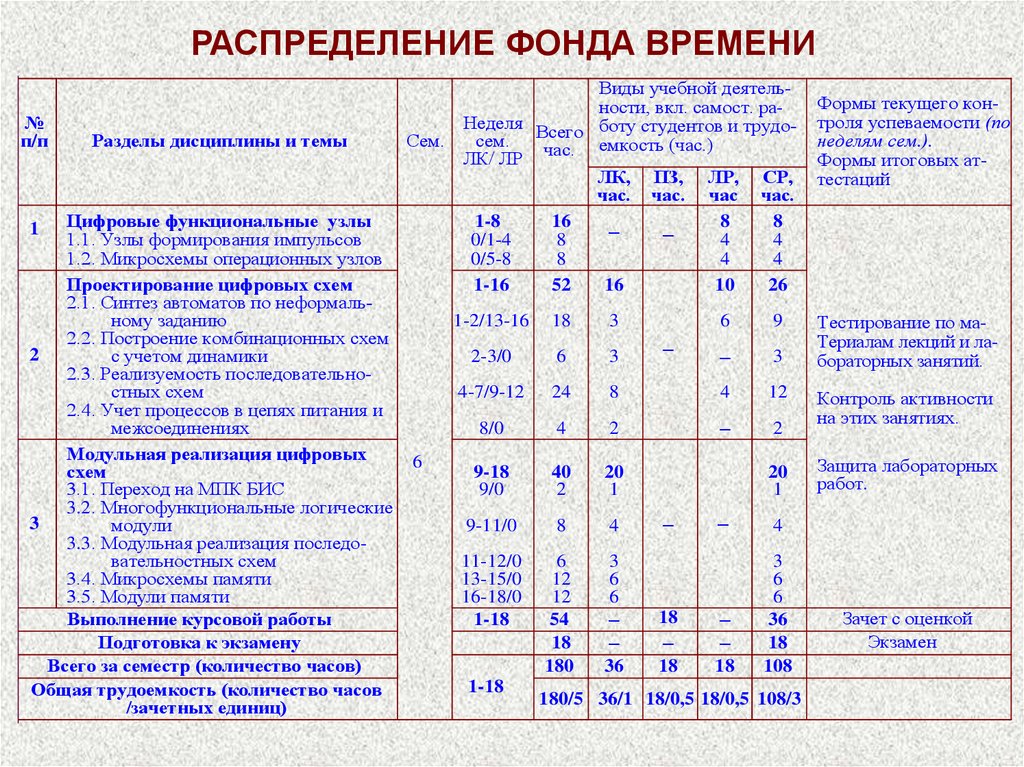
РАСПРЕДЕЛЕНИЕ ФОНДА ВРЕМЕНИ
№
п/п
Разделы дисциплины и темы
Цифровые функциональные узлы
1.1. Узлы формирования импульсов
1.2. Микросхемы операционных узлов
Проектирование цифровых схем
2.1. Синтез автоматов по неформальному заданию
2.2. Построение комбинационных схем
2
с учетом динамики
2.3. Реализуемость последовательностных схем
2.4. Учет процессов в цепях питания и
межсоединениях
Модульная реализация цифровых
схем
3.1. Переход на МПК БИС
3.2. Многофункциональные логические
3
модули
3.3. Модульная реализация последовательностных схем
3.4. Микросхемы памяти
3.5. Модули памяти
Выполнение курсовой работы
Подготовка к экзамену
Всего за семестр (количество часов)
Общая трудоемкость (количество часов
/зачетных единиц)
Сем.
1
6
Виды учебной деятельности, вкл. самост. раНеделя Всего боту студентов и трудосем.
час. емкость (час.)
ЛК/ ЛР
ЛК, ПЗ, ЛР, СР,
час. час. час час.
1-8
16
8
8
–
–
0/1-4
8
4
4
0/5-8
8
4
4
4
1-16
52
16
10
26
1-2/13-16
18
3
6
9
2-3/0
6
3
–
3
4-7/9-12
24
8
4
12
8/0
4
2
–
2
9-18
9/0
40
2
20
1
9-11/0
8
4
11-12/0
13-15/0
16-18/0
1-18
6
12
12
54
18
180
3
6
6
–
–
36
1-18
–
20
1
–
18
–
18
–
4
–
–
18
3
6
6
36
18
108
Формы текущего контроля успеваемости (по
неделям сем.).
Формы итоговых аттестаций
Тестирование по маТериалам лекций и лабораторных занятий.
Контроль активности
на этих занятиях.
Защита лабораторных
работ.
Зачет с оценкой
Экзамен
180/5 36/1 18/0,5 18/0,5 108/3
5

6.

ЛИТЕРАТУРА
• Райхлин В.А. Основы цифровой схемотехники. Уч.пособие. Изд-е 2. - Каз.:
Изд. КГТУ, 2006 (Изд-е 1 - 2000г.
http://www.bks-mgu.ru/fulltxt/a354.pdf )
• Райхлин В.А. Презентация лекций по схемотехнике.
http://modelling.kai.ru/sx.zip
• Райхлин В.А., Гибадуллин Р.Ф. Схемотехника ЭВМ. Уч. пособие по
практическим занятиям. – Казань: Изд. «Яз», 2013.
Цифровая схемотехника. Компьют. практикум. Ч.2. - Каз.: Изд. Экоцентр, 2006
Интерактивная система синтеза цифровых
автоматов. - Казань: АСОС КСЮИ, 2006
• Арсентьев С.А., Вершинин И.С.
• Райхлин В.А., Морозов А.В.
• Райхлин В.А.
Схемотехника ЭВМ. Методич. указания по курсовому
проектированию. - Казань: Изд. КГТУ, 1995
• Применение интегральных микросхем в ЭВТ /Под ред. Б.Н. Файзулаева
и Б.В. Тарабрина. - М.: Радио и связь, 1988
• Шило В.А.
Популярные цифровые микросхемы. Справочник. - М.:
Радио и связь, 1987
6

7.

Раздел 2
ПРОЕКТИРОВАНИЕ
ЦИФРОВЫХ СХЕМ
7

8.

Часть 1
ДИНАМИКА ЦИФРОВЫХ
АВТОМАТОВ
Лекции 1-4
8

9. Лекции 1-2(1/2). СИНТЕЗ ЦИФРОВЫХ АВТОМАТОВ ПО НЕФОРМАЛЬНОМУ ЗАДАНИЮ

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПОДХОДА
Понятия автомата и реализующей его схемы – это разные понятия. Обычно автомат его таблица переходов. Но как построить эту таблицу по неформальному
описанию проектируемого устройства ?
Исходное описание задано тройкой {X, Z, L}. Здесь L – отображение {Ir} {Or},
r=1,2,…, множества входных слов Ir = (x1-…-xk-…-xl)r во множество выходных Or
= (z1-…-zk-…-zl)r. Наборы xk = [x1…xM]k, zk = [z1…zN]k, k {1, }, – буквы входного
Х и выходного Z алфавитов, xi и zj {0,1}, k– номер такта, – длина слова.
Абстрактный автомат – это {X, Z, S, s0, η, ζ}. Здесь S – множество внутренних
состояний s = 1,2,…; s0 S – начальное внутреннее состояние; η и ζ – функции переходов и выходов, заданные таблицей переходов.
Рассматривается конечный автомат Мили. Строки таблицы переходов отмечаются символами внутренних состояний sk-1, а столбцы – значениями входов xk.
В каждой клетке таблицы слева обозначается следующее состояние sk = η(xk, sk-1), через запятую справа –значение выхода zk = ζ(xk, sk-1).
Никаких ограничений на язык задания не накладывается. При этом, если длина
входной последовательности не ограничена, то проблема представимости задания конечным автоматом алгоритмически неразрешима. И все же такой автомат может
быть построен, если привлечь элементы эвристики.
9

10.

Отображение L асинхронно, если для любых допустимых r и k из
{Ir} {Or} следует (x1-…- n{xk} -…-xl ) r (z1 -…-n{zk}-…-zl ) r, n = 1,2…,
т.е. n-кратное повторение k-входа вызывает такое же повторение k–выхода с
сохранением соответствия в целом. Иными словами, если неизменность входа в соседних тактах ассоциируется с продолжением такта. Асинхронным
отображениям отвечают таблицы, в которых переход в каждом такте завершается устойчивым состоянием. Такие таблицы называются асинхронными. Для них η(x, η(x,s)) = η(x,s); ζ(x, η(x,s)) = ζ(x,s). Понятие асинхронной таблицы не ассоциируется со способом реализации, наличием или
отсутствием синхронизации.
Если заданное L допускает повторение входов в соседних тактах без сохранения значений выхода, то получаемая таблица называется синхронной,
т.к. она исключает асинхронную реализацию устройства. Если же задание
вообще не допускает повторений входов в соседних тактах, то возможны оба
варианта таблицы.
Задачу синтеза автомата по не формальному заданию можно решить следующим образом. Сначала – специфицировать все состояния синтезируемого автомата согласно неформальному заданию. Затем – организовать переходы между выделенными состояниями. Процесс такой спецификации называется разметкой состояний, а второй этап – испытанием состояний. Соответственно внутреннее состояние автомата определяется как объект,
специфицированный кортежем <var x, z, ИНДЕКС>.
10

11.

Суть разметки состоит в определении перечня спецификаций. Разметка называется полной, если этот перечень учитывает все условия задания. Кортеж
в целом определяет и полное состояние, в котором автомат оказывается при переходе в данное внутреннее состояние. Это полное состояние называется состоянием разметки.
Атрибут ИНДЕКС в общем случае – это многокомпонентный вектор параметров задания (четность номера такта, кратность изменения некоторой входной
переменной и др.). Основная трудность – не только в определении состава индекса, но и в установлении правил изменения специфицирующих кортежей (правил следования) на этапе испытаний.
Канонический способ полной разметки – перечисление всевозможных значений специфицирующих кортежей. Получаемое при этом число состояний автомата обычно далеко от минимального.
Используемы далее обозначения:
xi – изменение xi из 0 в 1;
xi – изменение xi из 1 в 0;
x1x2 = -0 – действие входного слова длины 1, где значение xi безразлично; x1x2 =
0 (1 ) – действие входного слова 00-10 (11-10) длины 2.
Полные состояния перехода в специфицируемые состояния (состояния разметки) в асинхронных таблицах выделяются круглыми скобками.
Лабиринт – множество состояний с неизменным значением выхода, в котором автомат пребывает до тех пор, пока не наступит одно из правильных событий,
которые выводят автомат из лабиринта. Состояние входа в лабиринт принадлежит
11
лабиринту. Состояние выхода из лабиринта находится вне лабиринта.

12.

АВТОМАТЫ БЕЗ ОСОБЕННОСТЕЙ
Этапы синтеза
1. Разметка состояний автомата. Для каждого состояния справа от
синтезируемой таблицы переходов указывается специфицирующий его
кортеж согласно исходному описанию. Одновременно в асинхронном
варианте определяются значения функций переходов и выходов для состояний разметки (в данном случае эти состояния устойчивы). В синхронном варианте указанные значения изначально не определены. Поэтому в соответствующие клетки таблицы ставятся прочерки. Они доопределяются при испытании состояний.
2. Испытания состояний разметки на допустимые изменения входов.
Получаемые при этом переходы определяются разметкой и правилами
следования согласно заданию. Одновременно проверяется правильность
разметки. Разметка правильна, если при испытании любого состояния
не возникает неопределенности следующего состояния или значения выхода. Иначе разметка корректируется с повторением испытаний.
3. Минимизация построенной таблицы переходов. Здесь используются
известные методы.
12

13.

Пример 1. Устройство с 2 входами и 2 выходами такое, что:
1) x1 либо x2 дают z1z2 = 10 или 01 соответственно;
2) xi (i = 1, 2) либо неизменность входа сохраняют выход;
3) в каждом такте допустимо изменение лишь одного входа.
Правило 2 таблица асинхронна. Компонента ИНДЕКС отсутствует.
Каноническая полная разметка + испытания таблица рис.г. После минимизации (объединение состояний рис.г показано пунктиром) рис.в.
13

14.

Пример 2. Неформальное задание рис. а-в.
Возможна только синхронная таблица.
Кортеж – {Var x, ИНДЕКС – четность k}, компонента z отсутствует.
Разметка рис.г.
Таблица переходов рис.д.
Минимизация рис.2е.
14

15.

АВТОМАТЫ С ЛАБИРИНТАМИ
Пример 3. Устройство на 2 входа и 1
выход с двумя лабиринтами такое, что
1) выход из одного лабиринта является входом в другой;
2) для лабиринта 1 значение z = 0. Выход из лабиринта 1 – по наступлении
события {I1, I2}, где I1= 00– 01– 00–10,
I2= 00–10–01–11;
3) для лабиринта 2 значение z = 1. Выход из лабиринта 2 – по наступлении события{I3, I4}, где I3=00–11–10–01, I4 = I2.
Разметка состояний лабиринтов 1, 2
рис.а,б. Для {I1, I2} j=1, для {I3,
I4} j=0. Рис.в,г таблицы переходов для синхронного и асинхронного
вариантов.
По условию 1 все состояния входов
в любой лабиринт имеют нулевой индекс
и потому объединяются. Должны быть
объединены и все состояния выходов из
каждого лабиринта. В процессе испытаний переход из полного состояния {5, 01} должен рассматриваться как
результат действия второй буквы отрезка I1, т.е. идти в состояние 4, а не в 1.
15

16.

Лекции 2(1/2)-3. ПОСТРОЕНИЕ КОМБИНАЦИОННЫХ
СХЕМ С УЧЕТОМ ДИНАМИКИ
СОСТЯЗАНИЯ В КОМБИНАЦИОННЫХ СХЕМАХ
Инерционность элементов влияет не только на быстродействие, но и на протекание перех. процессов в КС. При смене вх. набора сигналы на вх. элементов КС
поступают неодноврем. (состязания сигналов) из-за разницы в длинах“путей” их формирования. Такие состяз. опасны, если они при-водят к появлению кратковременных
ложных импульсов на выходе.
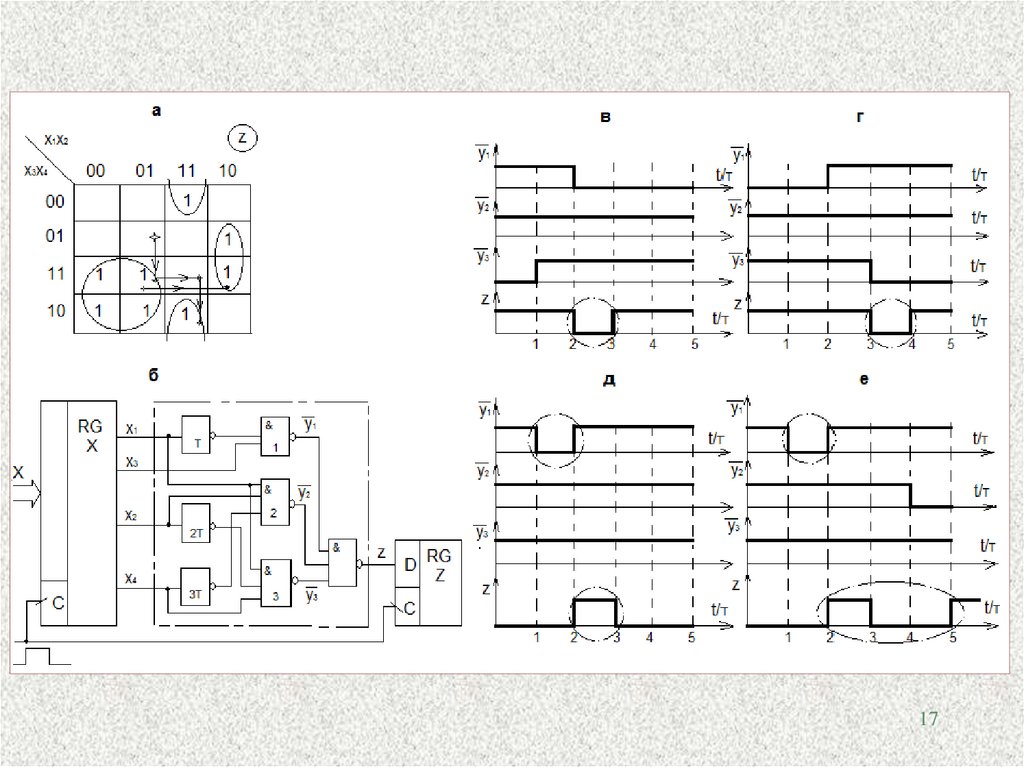
ПРИМЕР (рис. а). Из соображений минимизации:
z x1x3 x1x2 x4 x1 x2 x4 = y1 v y2 v y3
Полагаем, что входы схемы – прямые выходы RG X. Выход z – инф. вход Dтриггера. Соответствующая реализация – рис. б.
По условию:
•Задержки всех элементов И–НЕ КС одигнаковы и равны τ.
•Задержки инверторов показаны на рис. б.
•RG X переключается по фронту, а RG Z – по срезу СИ.
Рассмотрим ряд входных переходов.
1. x1x2x3x4 = 1011 → 0011 (рис. в).
В исходном состоянии сигнал z=1поддерживается импликантой x1 x3 (выход эл. 3), а
x4
по окончании перехода – импликантой x1 x 2 (выход
эл. 1). Наличие инвертора по x1
приводит к появлению на выходе z кратковременного ложного 0 (отрицательного импульса длительностью τ) – статическое 1-со-стязание (риск сбоя в 0) между сигна16
лами y1 и y3.

17.

17

18.

Положение можно исправить, если ввести импликанту x 2 x3 x4 , которая сохраняет
единицу на данном переходе. Аналогичное состязание будет наблюдаться на переходе x1x2x3x4 = 1110 → 0110 из-за отсутствия импликанты x2 x3 x 4 . Такие состязания
носят название логических, ибо их можно устранить логическим путем выполнением всех «склеек» на карте Карно.
2. x1x2x3x4 = 0111→ 1011 (рис. г).
Как и в первом случае, здесь имеем статическое состязание между сигналами y1
и y3. Но в этом состязании принимают участие уже 2 инвертора (по x1 и x2) c разными задержками, что приводит к появлению на выходе ложного 0 длительностью τ.
В данном случае устранить риск сбоя логическим путем принципиально невозможно. Поэтому такое состязание относят к числу функциональных (присущих
самой функции).
3. x1x2x3x4 = 0101→ 1111 (рис. д).
Здесь имеем случай статического 0-состязания – также функционального.
4. x1x2x3x4 = 0101→ 1110 (рис. е).
Состязание на этом переходе – динамическое (выход меняется не менее трех
раз) функциональное.
Чтобы избежать ошибочной установки RG Z, следует выбирать tси > tКС max , что
не всегда удается.
18

19.

АНАЛИТИЧЕСКОЕ ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ
В КОМБИНАЦИОННЫХ СХЕМАХ
Для получения полной картины возмож. вариантов врем. процессов в КС
в условиях разброса задержек эл. исп. аналитич. описание перех. процесса с
пом. операций бесконечнозначной (непрерывной) логики, прим. к исчисл. не
состояний устройства, а моментов изменений сигн. При этом скачок 0 1
в мом. обозн. как 1 α ; скачок 1 0 в мом. – как 0β ; импульс – как
1 α 0β , или 1( , ); паузу – как 0 α1β , или 0( , ).
Если процесс содержит несколько импульсов и пауз, то моменты изменений указываются 1 раз. Например, 0 αβ 1 γ 0 α γ 0(αβ, γ)1 ( , α γ). Постоянный сигнал 0 (1) трактуется как импульс (пауза) нулевой длительности:
0 = 1( , ), 1 = 0( , ). Операция дизъюнкции – как = mах( , ).
Конъюнкция – как = = min( , ).
Процедура отыскания перех. процесса в КС при смене вх. набора:
1. Замена каждого реального эл. соотв. идеальным (безынерц.) и последоват. вкл. с ним эл. задержки.
2. Представление каждого идеального эл. экв. схемой в булевом базисе.
3. Упорядочение полученной схемы по уровням.
4. Вычисление перех. процесса на вых. путем последоват. подстановок.19

20.

При этом достаточно уметь находить реакции эл. задержки, инвертора
~
и 2-вх. эл. И, ИЛИ на ступ. возд. вида x(t ) a ( 1 , 2 ) a ( , 3 ) a m ( m 1 , m ) , где
~
~
а {0, 1}, a - отрицание а, am a при m чет. и am a , если m нечет.
Процесс на вых. эл. задержки ( –задержка) z(t) = x(t) = a( 1+ , 2+ )
~
a (–, 3+ )… a m ( m-1+ , m+ ). Для инвертора z(t) =x(t) =a (α1,α2)a(-, α3) …
~
am-1 (α m 1, α m ) , т. е. процесс на вых. пол. из вх. заменой импульсов на паузы и
пауз на импульсы в тех же врем.интервалах. Для 2-вх. эл. И, ИЛИ: Если 1-вх.
– х(t) – одиноч. ступень, а др. – у(t) содержит нек. число импульсов и пауз, то
z(t) нах. путем полного перебора всех возмож. вариантов взаим. располож.
моментов изм. сигналов. и объед. частн. реш. с прим. б/знач. логики.
Пусть x(t) = 1 и у(t) = 0 . Тогда
В случае
1( , ),
z (t ) x (t ) y (t ) 1 0
0 1( , ),
x(t) 0 α , y(t) 0 β1 γ
;
1(α , α β).
. =
0( , ), ;
z (t ) x(t ) y (t ) 0 0 1 0( , ), ;
0(α β, α γ).
1 0( , ), .
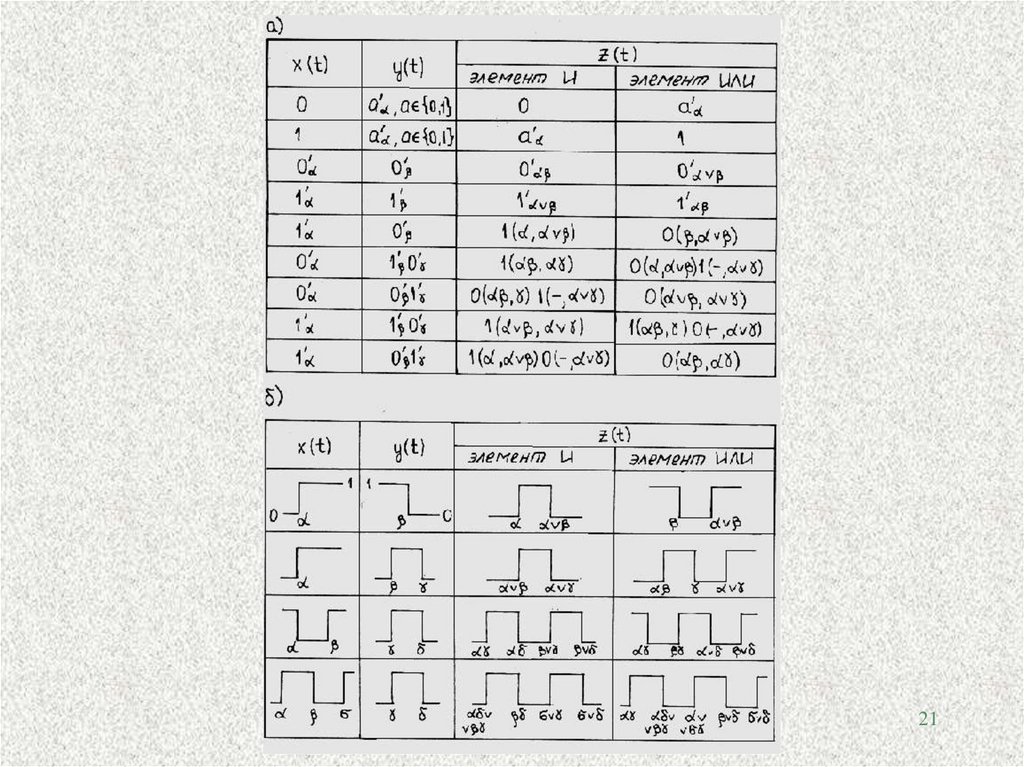
Варианты z(t), когда в у(t) – не более 1 имп. (паузы) привед. в табл.а.20

21.

21

22.

Реакции 2-входовых элементов И (ИЛИ) на входные воздействия с большим числом изменений сигнала можно вычислить методом декомпозиции.
Согласно ему одно из двух входных воздействий, например x(t), разбивается
на два следующих друг за другом более простых x1(t) и x2(t), так чтобы
1 =
первый из них заканчивался изменением сигнала вида
( )0и x(t)
x1(t)x2(t). Затем находятся реакции элементов z1(t) и z2(t) на пары воздействий {x1(t), у(t)} и {x2(t), у(t)} соответственно. Если z1(t) и z2(t) не пересекаются во времени, то полная реакция элемента z(t) = z1(t)z2(t) .
В качестве примера найдем переходный процесс на выходе элемента И
при x(t) = 0 1 , у(t) = 1 0 . Принимаем х1(t) = 0 , х2(t) =1 . Согласно табл. а)
находим
z1 (t ) 0 1 0 1( , ); z 2 (t ) 1 1 0 1( , ).
Поскольку > , то процессы не пересекаются и между
ними должна быть пауза. Соответственно
0 1 1 0 1( , ) 0( , ) 1( , ).
При тех же воздействиях на выходах элемента ИЛИ разбивать следует
сигнал y(t). Аналогично получаем
0 1 1 0 0( , ) 1( , ) 0( , ).
Построенные таким образом графики (табл. б) иллюстрируют усложне22
ние переходного процесса в комбинационной схеме от уровня к уровню.

23.

ЛОГИКО-СТРУКТУРНЫЕ МЕТОДЫ УСТРАНЕНИЯ КОМБИНАЦ.
СОСТЯЗАНИЙ
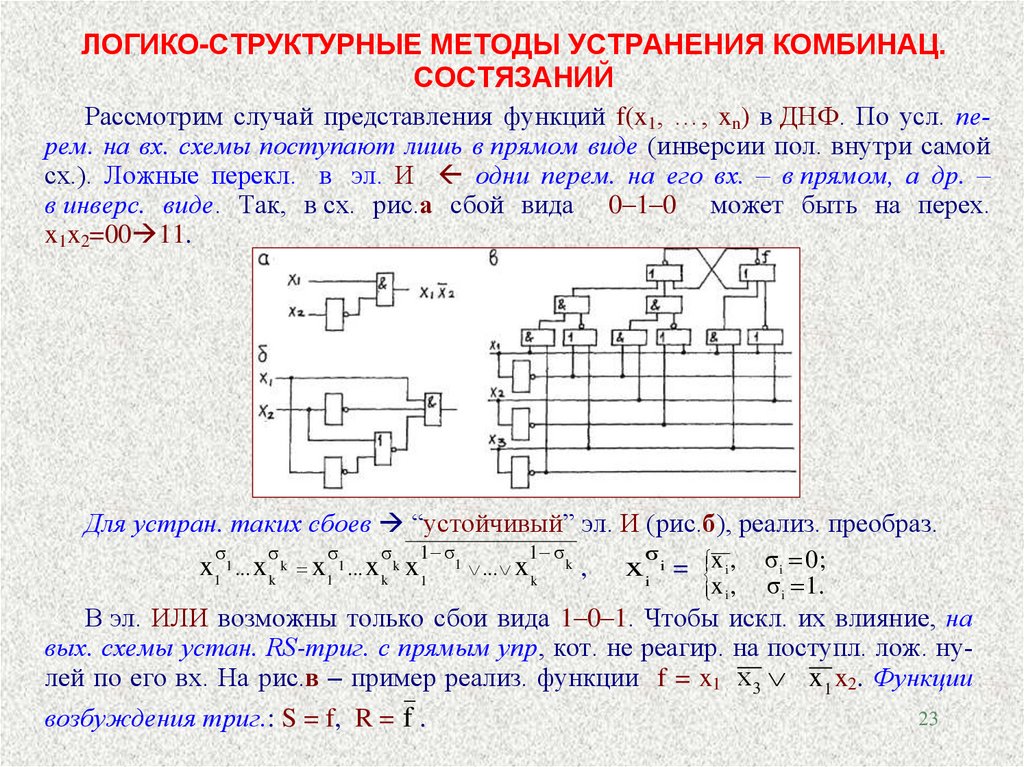
Рассмотрим случай представления функций f(x1, …, xn) в ДНФ. По усл. перем. на вх. схемы поступают лишь в прямом виде (инверсии пол. внутри самой
сх.). Ложные перекл. в эл. И одни перем. на его вх. – в прямом, а др. –
в инверс. виде. Так, в сх. рис.а сбой вида 0–1–0 может быть на перех.
x1x2=00 11.
Для устран. таких сбоев “устойчивый” эл. И (рис.б), реализ. преобраз.
σ
σ
σ
σ
1 σ
x1 1 ... x k k x1 1 ... x k k x1
1 ...
1 σ
xk
k
,
σ
x i i = x i , σi 0;
x,
i
σi 1.
В эл. ИЛИ возможны только сбои вида 1–0–1. Чтобы искл. их влияние, на
вых. схемы устан. RS-триг. с прямым упр, кот. не реагир. на поступл. лож. нулей по его вх. На рис.в – пример реализ. функции f = x1 х 3 x1 x2. Функции
23
возбуждения триг.: S = f, R = f .

24.

Лекция 4. СОСТЯЗАНИЯ В АСИНХРОННЫХ
ПОСЛЕДОВАТЕЛЬНОСТНЫХ СХЕМАХ
При смене входных наборов правильное логическое функционирование
многотактной асинхронной схемы могут нарушить статические, существенные либо критические состязания.
1. Статические состязания
Они могут возникнуть в случае, когда смена входных наборов не должна
приводить к изменению внутр. переменной. Речь в данном случае идет о
влиянии комб. состяз. на функц. схем с ОС.
В схеме рис.а функция Y = x 2 x 1 x 2 y x 2 x 1 x 2 y. Соотв. объед. показ. на
карте Карно. Обозн. через 1 и 2 задержки эл.1 и 2. Пусть сначала
х1х2=10. Тогда Y(0)=1 и при смене вх. набора на х1х2=11 возможен переход
в ошиб. сост. Y=0, если 1 > 2. Опасность сбоя в данном случае можно
x x1y
устранить эквив. преобраз. схемы (рис.б; Y= 2
) путем вып. всех
“склеек” на карте Карно, так чтобы смена вх. с сохр. сигнала ОС происх. всегда внутри нек. покрытия (рис.б; штриховка). Но если переход к новому
такту связан с изм. неск. вх. сигналов либо на переходе меняется неск.
внутр. переменных (при пост. рассматриваемой), то статич. комб. состязания могут быть функциональными. Здесь уже надо прим. спец. методы.24

25.

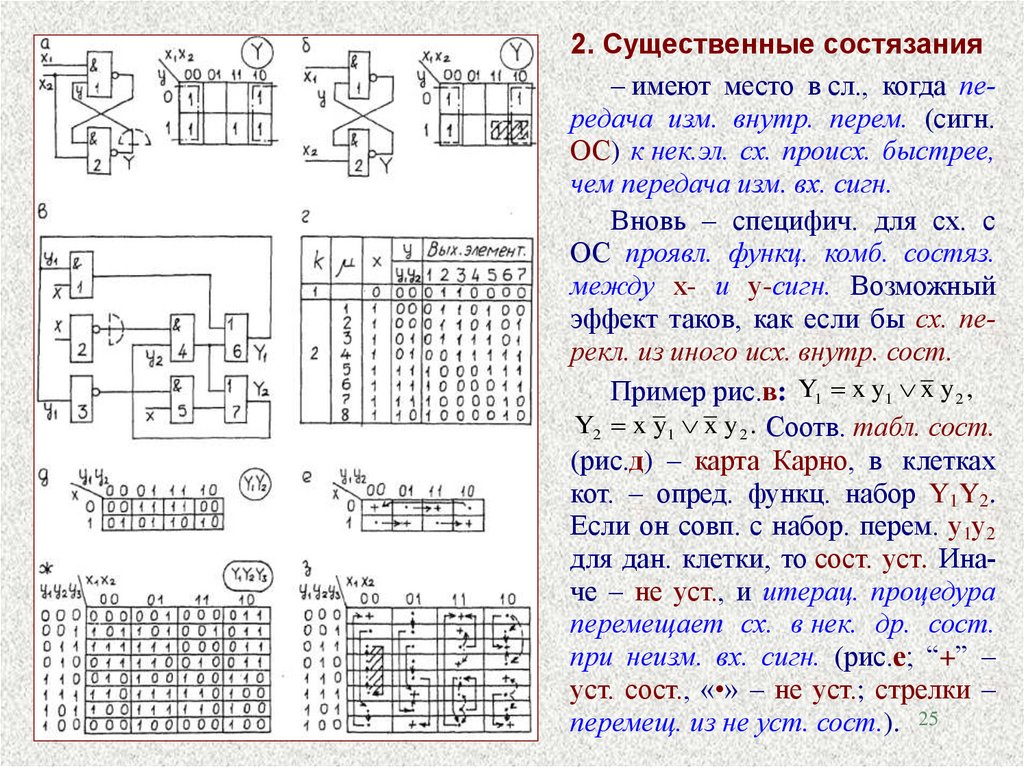
2. Существенные состязания
– имеют место в сл., когда передача изм. внутр. перем. (сигн.
ОС) к нек.эл. сх. происх. быстрее,
чем передача изм. вх. сигн.
Вновь – специфич. для сх. с
ОС проявл. функц. комб. состяз.
между х- и у-сигн. Возможный
эффект таков, как если бы сх. перекл. из иного исх. внутр. сост.
Пример рис.в: Y1 x y1 x y 2 ,
Y2 x y1 x y 2 . Соотв. табл. сост.
(рис.д) – карта Карно, в клетках
кот. – опред. функц. набор Y1Y2.
Если он совп. с набор. перем. у1у2
для дан. клетки, то сост. уст. Иначе – не уст., и итерац. процедура
перемещает сх. в нек. др. сост.
при неизм. вх. сигн. (рис.е; “+” –
уст. сост., «•» – не уст.; стрелки –
перемещ. из не уст. сост.). 25

26.

Правило Ангера: существ. состязания имеют место лишь в случае, если
в таблице найдено такое исх. состояние Y(0) и такой вх. набор Ii , что 3
последоват. изм. Ii - Ij перевод. сх. в сост., отлич. от того, в каком она
оказ. после 1-изм.
Это – в нашем примере (рис.е).
Рассм. особенности перех. процессов в сх. (рис.в; повыш. инерцион. эл.2
– введена доп. задержка – пунктир). Пусть i = , i 2, и в исх. сост. х
= 0, у1у2 = 00. Итерац. моделир. по микротактам показ., что при смене вх.
сигн. х = 0 – 1 прав. комб. у1у2 = 01 устан. лишь в сл. 2 = или 2 .
Если 2 = 3 , то – колебат. процесс у1у2 = 00 11 00 … . При 2
= 4 (рис.г) и > – ошиб. переход в сост. у1у2 = 10. Причина тому – появл.
кратковрем. лож. 1 на вых. эл.4, к кот. изм. у2 перед. быстрее, чем изм. х.
3. Критические состязания
– выявл. непосред.по табл. сост. Могут иметь место, когда содерж.
клетки отлич. от соотв. ей набора внутр. перем. двумя и > комп. и возможен переход от дан. не уст. в разные уст. сост. Состяз. – не критич.,
если конеч. уст. сост. единств.
В примере (рис.ж,з; в столбце х1х2=00 штрих. выделен колебат. цикл)
критич. состяз. возник. в столб. х1х2 = 11 (верх) и 10 (низ), не критич. – в
26
столб. х1х2 = 11 (низ) и 10 (верх).

27.

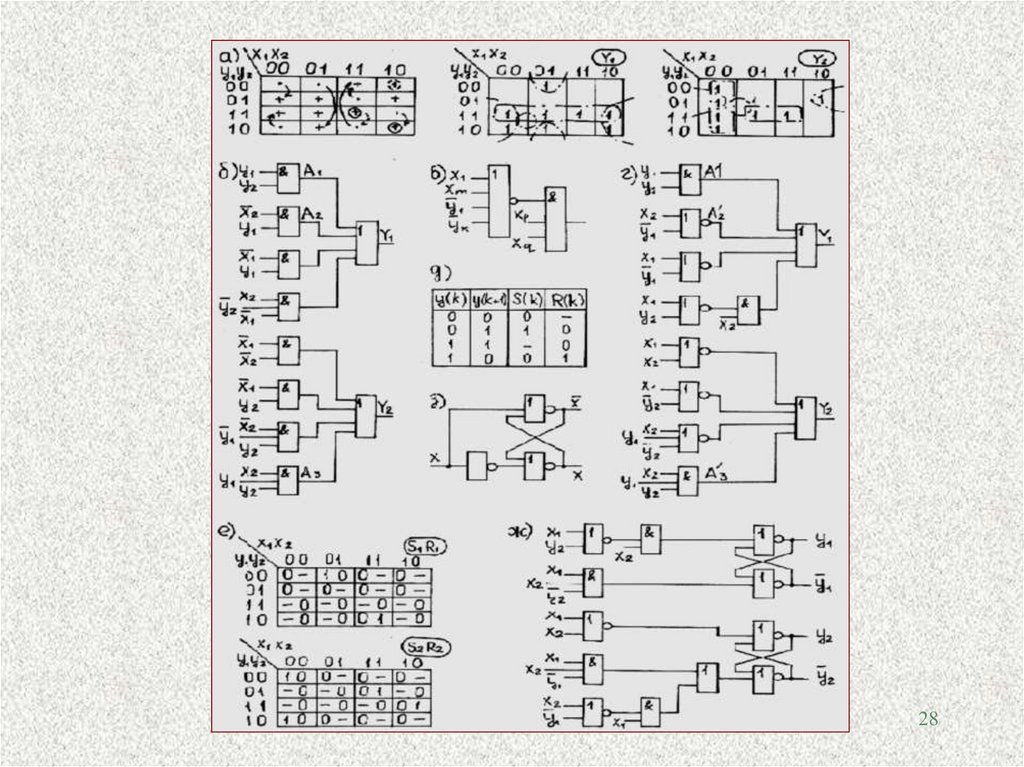
4. Устранение существенных состязаний
Пример схемы (рис.б) с существенными состязаниями (рис.а). Пусть нач.
сост. x1x2y1y2=1111 и x2=1-0. Тогда вых. эл. A3 – 0. Если задержка пол. x 2 ср.
велика,то var.y2 достигает вх. эл.A1 раньше, чем на вх. эл.A2 сигн. x 2 :=1. При
этом var. y2 прояв. в узле Y1 раньше, чем var. x2. Схема ведет себя так, как если бы ее сост. var. с 1111 на 1110 (рис. а; пунктир. перех.). В конеч. итоге схема придет в сост. 1000 (рис.а; пунктир) вместо 1010.
Устранение состяз. на ур. эл. И ИЛИ-НЕ/И–парная факторизация:
x1...x m x p...xq y1...yk x1 ... xm y1 ... yk x p...xq .
Ей отвечает эл. на рис.в сх. рис.г. В случае изменения одного вх. вместо факторизации прим. асинхр. D–триг. на эл. ИЛИ–НЕ (рис.з) для форм. xi и
x i . Тогда задерж. только изменения xi и x i из 0 в 1. Поэтому единственно возмож. сбой 0-1-0 для эл. И отсут. Но если задержка эл. A2’ ср. велика, то – перенос сбоя с ур.1 на ур.2.
Устранение состяз. на ур. эл. ИЛИ RS-триг. с прямым упр. для форм. yi.
Функции S и R по табл. возбуждений (рис.е) из табл. сост. рис.а по правилам рис.д. При этом не надо выявлять все простые импликанты. В данном
случае
S1= x1x 2 y2 ; R1=x1x2 y2 ; S2= x1 x 2 ; R2=x1x2 y1 x1 x 2 y1.
Окончат. реализация – рис.ж. Целесообразно ее вып. на эл. И-ИЛИ-НЕ. 27

28.

28