Похожие презентации:
Теория принятия решений. Лекция №11-12
1.
Южный федеральный университетИнститут компьютерных технологий и информационной безопасности
Презентация к лекциям №11, 12
по дисциплине
«Теория принятия решений»
Лектор:
к.т.н., доцент каф. СиПУ
Кузьменко А.А.
andrew.kuzmenkosipu@gmail.com
2.
Лекция №11Цель лекции:
– сформулировать постановку задачи принятия решений при
полной информации;
– изучить нелинейные распределительные задачи принятия
решений.
Содержание лекции:
1. Задачи принятия решений при полной информации.
2. Нелинейные распределительные задачи.
3. Пример построения модели и вычислительной схемы для задачи
распределения.
2
3.
1. Задачи принятия решений при полнойинформации
Задача принятия решений при полной информации (в условиях
определённости) — это задача, в которой имеется полная и
исчерпывающая информация о состоянии внешней среды, необходимая
для принятия решения, т.е. проблемная ситуация не требует
доопределения.
При принятии решения в условиях определённости состояние среды
является фиксированным и оно известно ЛПР. В этом случае результат
решения (исход) однозначно определяется выбором альтернативы,
поэтому выбор альтернативы здесь будет эквивалентен выбору исхода:
3
Y X.
4.
Таким образом, исследование математической модели задачи ПР в условияхопределённости сводится к трём шагам:
указанию множества допустимых альтернатив X;
заданию целевых функций: Fj(Xi);
нахождению наилучшего (максимума или минимума) / компромиссного
решения.
Детерминированные задачи математического программирования являются
задачами ПР в условиях определённости.
При рассмотрении математических моделей задач ПР возникают два
основных вопроса:
1) существует ли оптимальное решение
и
2) если оптимальное решение существует, то как его найти.
В случае, когда существует множество допустимых альтернатив обе
проблемы легко разрешимы. Но нет простого и универсального метода
решения задач математического программирования.
4
Однако разработаны методы решения для отдельных классов задач.
5.
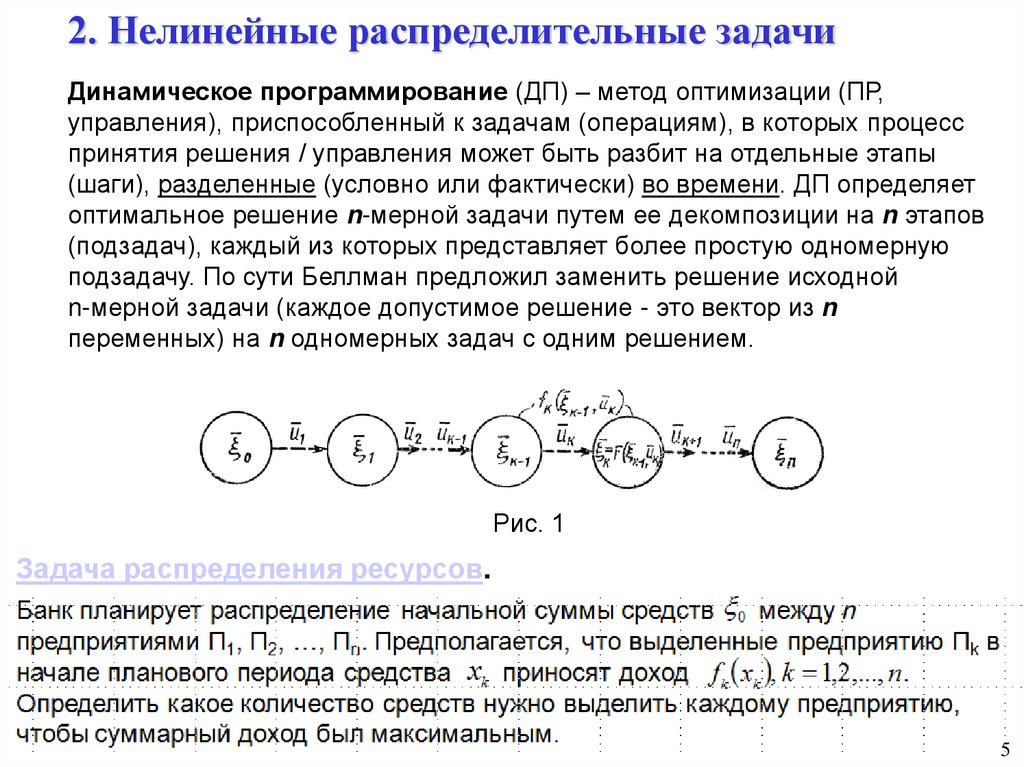
2. Нелинейные распределительные задачиДинамическое программирование (ДП) – метод оптимизации (ПР,
управления), приспособленный к задачам (операциям), в которых процесс
принятия решения / управления может быть разбит на отдельные этапы
(шаги), разделенные (условно или фактически) во времени. ДП определяет
оптимальное решение n-мерной задачи путем ее декомпозиции на n этапов
(подзадач), каждый из которых представляет более простую одномерную
подзадачу. По сути Беллман предложил заменить решение исходной
n-мерной задачи (каждое допустимое решение - это вектор из n
переменных) на n одномерных задач с одним решением.
Рис. 1
Задача распределения ресурсов.
5
5
6.
Задача о замене оборудования.6
6
7.
Предположим, что процесс решения (управления) можно разбить на n шагов.Состояние системы после k-го шага (k=1,2,…,n) характеризуется параметром k .
Последовательный переход системы из одного состояния в другое
обеспечивается соответствующими решениями (управлениями) u1 , u2 ,..., un
которые составляют управление системой U u1 , u2 ,..., un .
Т.о, рассматривается управляемая система, которая под влиянием управления
(решения) переходит из начального состояния 0 в конечное состояние n.
1. Черта над символом означает векторную величину.
2. Управление на k-м шаге может быть не только количественным, но и
качественным (например, заменить/сохранить оборудование).
3. Целевая функция в зависимости от сущности задачи может как
максимизироваться (прибыль, доход, фондоотдача, производительность,
надежность и др.), так и минимизироваться (затраты, потери,
7
себестоимость).
8.
Задачи ДП всегда должны обладать свойством отсутствия последействия :состояние системы после k-го шага зависит только от
k
предшествующего состояния
и управления u на данном шаге и не
k 1
k
зависит от управлений на предыдущих шагах. Это свойство
формализуется уравнением состояния :
k Fk k 1 , uk
(1)
Варьируя управления, получим разную «эффективность» процесса,
которую будем оценивать количественно целевой функцией:
n
Z f k k 1 , u k
k 1
(2)
Здесь f k k 1 , u k – показатель эффективности k-го шага (локальная
целевая функция), который зависит от состояния в начале этого шага и
управления на данном шаге. В общем случае показатель эффективности –
нелинейная функция. Целевая функция задачи ДП всегда должны быть
аддитивной.
Обычно условиями задачи на управления на каждом шаге могут
накладываться некоторые ограничения. Управления, удовлетворяющие
этим ограничениям, называются допустимыми.
Управление, при котором достигается экстремум целевой функции,
называется оптимальным управлением и обозначается U * u1* , u2* ,..., un* .
8
9.
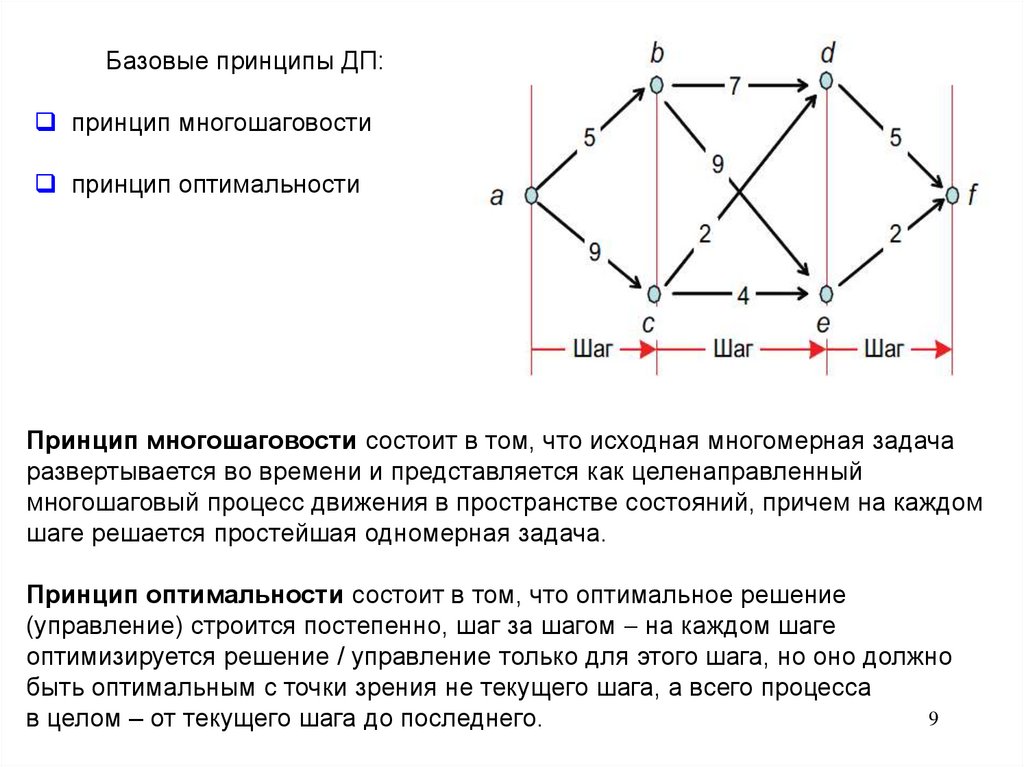
Базовые принципы ДП:принцип многошаговости
принцип оптимальности
Принцип многошаговости состоит в том, что исходная многомерная задача
развертывается во времени и представляется как целенаправленный
многошаговый процесс движения в пространстве состояний, причем на каждом
шаге решается простейшая одномерная задача.
Принцип оптимальности состоит в том, что оптимальное решение
(управление) строится постепенно, шаг за шагом на каждом шаге
оптимизируется решение / управление только для этого шага, но оно должно
быть оптимальным с точки зрения не текущего шага, а всего процесса
9
в целом – от текущего шага до последнего.
10.
Р. Беллман в 1953 г. сформулировал принцип оптимальности:в интерпретации Е.С. Вентцель:
каково бы ни было состоянии системы в результате какого-либо числа
шагов, на ближайшем (текущем) шаге нужно выбирать решение так, чтобы
оно в совокупности с оптимальным решением на всех последующих шагах
приводило к оптимальному выигрышу на всех оставшихся шагах, включая
данный.
10
11.
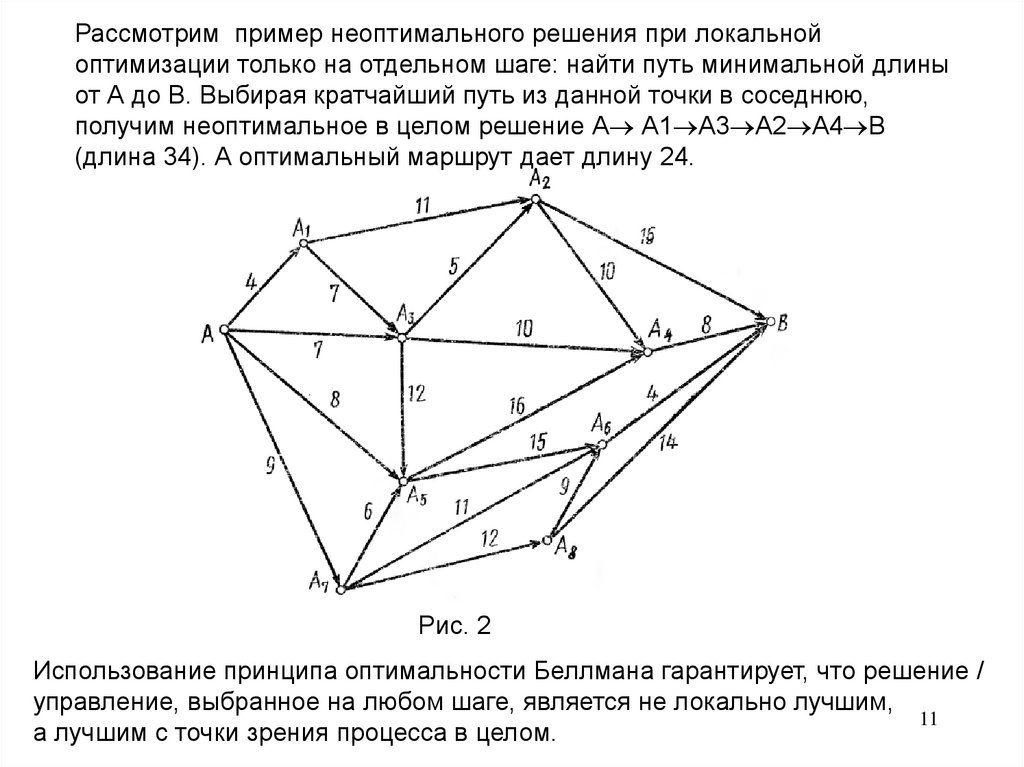
Рассмотрим пример неоптимального решения при локальнойоптимизации только на отдельном шаге: найти путь минимальной длины
от А до В. Выбирая кратчайший путь из данной точки в соседнюю,
получим неоптимальное в целом решение А А1 А3 А2 А4 В
(длина 34). А оптимальный маршрут дает длину 24.
Рис. 2
Использование принципа оптимальности Беллмана гарантирует, что решение /
управление, выбранное на любом шаге, является не локально лучшим,
11
а лучшим с точки зрения процесса в целом.
12.
Аналитически принцип оптимальности записывается в видеосновного функционального уравнения ДП (уравнения
Беллмана / рекуррентного уравнения Беллмана):
Z k* k 1 max f k k 1 , u k Z k* 1 k
uk
(3)
Z k* k 1 условный максимум на k-м шаге.
ВАЖНО! Уравнение (3) имеет достаточно общий характер и для каждой конкретной
задачи должно быть записано с учётом индивидуальных свойств этой задачи, в т.ч. может
рассматриваться задача минимизации.
Схематически уравнение Беллмана (3) иллюстрируется на рис. 3.
Рис. 3
12
13.
Вычислительный алгоритм построение модели ДП:1. Выбирают способ деления процесса (задачи) на шаги.
2. Вводят параметры состояния k и переменные управления u k на каждом шаге.
3. Записывают уравнение состояния:
k Fk k 1 , uk
(4)
4. Вводят показатели эффективности на k-м шаге f , u и суммарную
k
целевую функцию:
n
Z f k k 1 , u k
k 1
k 1
k
(5)
5. Из ограничений задачи определяют для каждого шага из множества Dk
допустимые решения (управления) на этом шаге.
6. Записывают основные для вычислительной схемы ДП функциональные
уравнения Беллмана
Z k* k 1 max f k k 1 , u k Z k* 1 k
и
u k Dk
Z n* n 1 max f n n 1 , u n
u n Dn
(6)
(7)
7. Определяют условные максимумы Z k* k 1 показателя эффективности от k-го
шага (включительно) до конца процесса и условные оптимальные управления
на k-м шаге uk* k 1 .
13
14.
Несмотря на единообразие данного алгоритма, для конкретной задачи ДП онадаптируется с учетом размерности задачи, характера модели (дискретная или
непрерывная) и др.
Замечания по реализации алгоритма:
1. Решение задачи проводят последовательно: начинают с (7) k=n, далее по (6)
до k=1 – обратный ход. Этот первый этап называется условной оптимизацией.
2. В результате последовательного решения n частных подзадач на условный
максимум на каждом шаге определяются две последовательности функций:
Z – условные максимумы
*
k
k 1
u – условные оптимальные управления
*
k
k 1
3. Указанные последовательности функций в дискретных задачах получают в
табличной форме, а в непрерывной моделях – аналитически.
4. После выполнения этапа условной оптимизации приступают ко второму этапу –
этапу безусловной оптимизации :
*
а) если начальное состояние 0 задано, то непосредственно определяют
*
максимум целевой функции всей задачи в целом Z max Z1* 0 ,
а затем – искомое безусловное оптимальное управление по цепочке:
*
*
*
*
*
*
*
(8)
0 u1 1 u2 2 ... un n .
В этой цепочке переход, указанный стрелкой , проводят по
последовательности uk* k 1 , а указанный стрелкой – с помощью
уравнения состояния.
14
15.
б) если задано множество 0 , 0 0 начальных состояний, то дополнительнорешают еще одну задачу максимизации:
Z max max Z1* 0 ,
0 0
*
откуда находят 0 , а затем по цепочке (8) находят безусловное оптимальное
управление.
Выше описан алгоритм решения задач ДП называемый обратным ходом
(от конца в начало задачи). В теории ДП имеется и алгоритм прямого хода.
Объем вычислений обоих подходов равнозначен, но при некоторых
дополнительных исследованиях предпочтительнее становится тот или иной
подход.
15
16.
3. Пример построения модели и вычислительнойсхемы для задачи распределения
Задача (общая формулировка).
Банк планирует распределение начальной суммы средств 0 между n
предприятиями П1, П2, …, Пn. Предполагается, что выделенные предприятию Пk в
начале планового периода средства xk приносят доход f k xk , k 1,2,..., n .
Определить какое количество средств нужно выделить каждому предприятию,
чтобы суммарный доход был максимальным.
Допущения задачи:
1) доход, полученный от вложения в одно предприятие не зависит от вложения в
другие предприятия;
2) доходы, получаемые от разных предприятий, выражаются в одинаковых
единицах;
3) общий доход равен сумме доходов, полученных от распределения всех средств
по всем предприятиям;
4) начальная сумма распределяется без остатка.
16
17.
Запишем математическую модель задачи.1. Определяем количество шагов (этапов) задачи:
исходя из свойства процесса распределения средств, целесообразно
представить его как n-шаговый процесс: за номер шага примем номер
предприятия.
2. Определяем переменные состояния и управления:
исходя из свойства процесса, в качестве решения (управлений) будем
рассматривать объем выделяемых средств xk k-му предприятию.
Тогда переменные состояния на каждом шаге – это остаток средств, подлежащих
распределению. Т.е. исходя из начального состояния 0 , после первого шага, на
котором выделено x1 средств 1-му предприятия, остаток составит 1 0 x1 .
При этом задача имеет ограничение:
n
x , x 0.
k 1
k
0
k
3. Записываем уравнения состояния:
k k 1 xk , k 1, n
4. Суммарный доход – целевая функция:
n
Z f k xk
k 1
17
18.
5-7. Сформируем уравнения Беллмана.Рассмотрим k-й шаг. Очевидно, что xk можно выбирать из условия 0 xk k 1.
Это неравенство формирует множество допустимых управления для k-го шага.
Формируем уравнения Беллмана из рассуждений:
выделив величину xk и получив от k-го предприятия доход f k xk , мы должны
распорядиться оставшимися средствами k k 1 xk наивыгоднейшим образом и
получить от предприятий Пk+1,…, Пn максимальный доход Z k* 1 k . Таким образом
*
величину xk следует определять из условия максимизации суммы f k xk Z k 1 k .
Отсюда уравнение Беллмана для нашей задачи
Z k* k 1 max f k xk Z k* 1 k .
0 xk k 1
Перейдем к вычислительной схеме. Нас интересует Z1* 0 , но если начать с
1-го шага
Z * max f x Z * ,
1
0
0 x1 0
1
1
2
1
то необходимо знать Z 2* 1 . Аналогично для других шагов. Однако имеется шаг, за
которым нет последующего. Это последний шаг. Для него
Z n* n 1 max f n xn .
0 xn n 1
Поскольку функция дохода f n xn монотонно возрастает, поэтому решением этой
*
задачи является условное управление xn n 1 , при котором достигается условный
максимум Z n* n 1 f n xn* . Таким образом, эту задачу целесообразно
18
решить, используя обратный ход.
19.
В результате обратного хода (последовательно проходя все шаги с конца процессак его началу) получим для каждого шага две последовательности:
- условные максимальные доходы
Z n* n 1 , Z n* 1 n 2 ,..., Z 2* 1 , Z1* 0
- условные оптимальные управления
xn* n 1 , xn* 1 n 2 ,..., x2* 1 , x1* 0 .
Этим завершен этап условной оптимизации. Теперь переходим к безусловной
оптимизации. На этом этапе, зная значение Z1* 0 , по заданному изначально
значению 0 определяем Z max Z1* 0 . Далее, выделяем x1* 0 1-му предприятию,
*
тогда для распределения остается 1 0 x1 . По этой величине определяем
*
оптимальное количество средств x2 1 , выделяемых 2-му предприятию, и т.д. пока
не будет определен весь вектор управления.
Основной недостаток метода ДП – это «проклятие размерности», т.е.
увеличение размерности задачи приводит к существенному увеличению объема и
времени вычислений.
19
20.
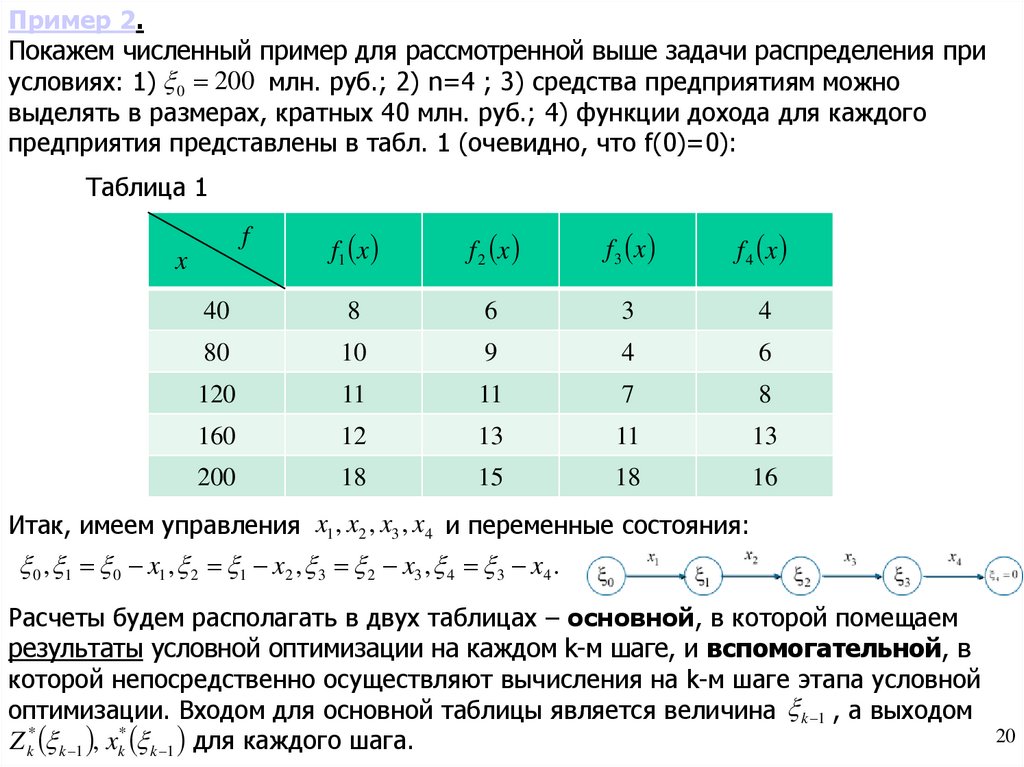
Пример 2.Покажем численный пример для рассмотренной выше задачи распределения при
условиях: 1) 0 200 млн. руб.; 2) n=4 ; 3) средства предприятиям можно
выделять в размерах, кратных 40 млн. руб.; 4) функции дохода для каждого
предприятия представлены в табл. 1 (очевидно, что f(0)=0):
Таблица 1
f1 x
f 2 x
f 3 x
f 4 x
40
8
6
3
4
80
10
9
4
6
120
11
11
7
8
160
12
13
11
13
200
18
15
18
16
f
x
Итак, имеем управления x1 , x2 , x3 , x4 и переменные состояния:
0 , 1 0 x1 , 2 1 x2 , 3 2 x3 , 4 3 x4 .
Расчеты будем располагать в двух таблицах – основной, в которой помещаем
результаты условной оптимизации на каждом k-м шаге, и вспомогательной, в
которой непосредственно осуществляют вычисления на k-м шаге этапа условной
оптимизации. Входом для основной таблицы является величина k 1 , а выходом
20
Z k* k 1 , xk* k 1 для каждого шага.
21.
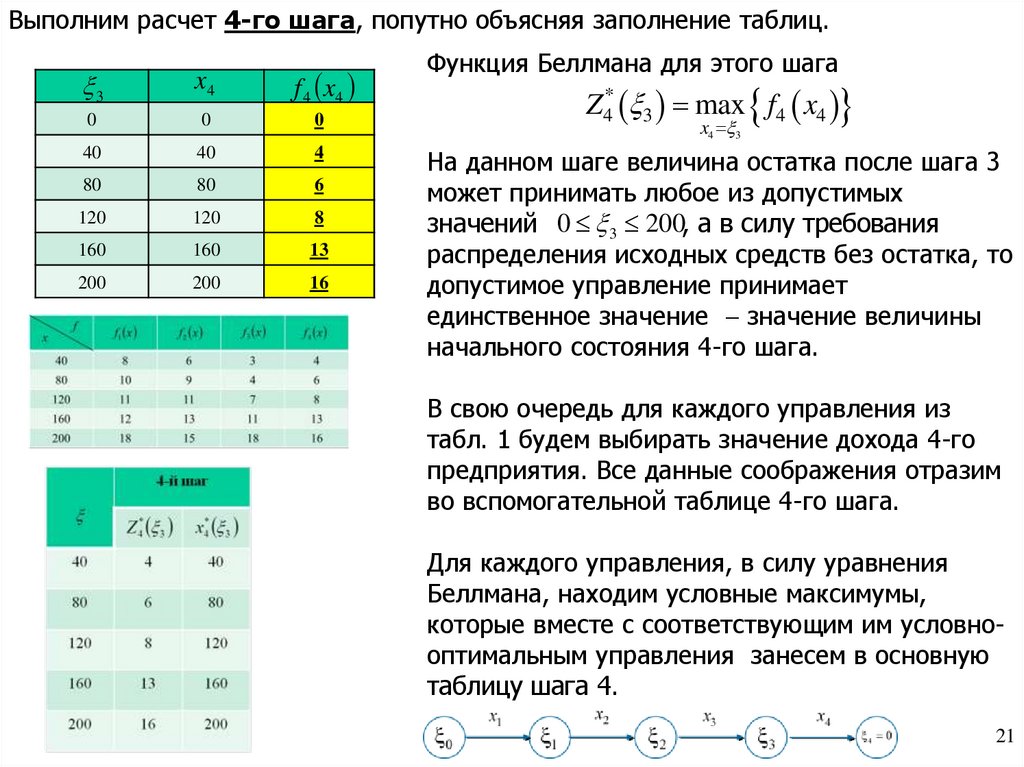
Выполним расчет 4-го шага, попутно объясняя заполнение таблиц.3
x4
f 4 x4
0
0
0
40
40
4
80
80
6
120
120
8
160
160
13
200
200
16
Функция Беллмана для этого шага
Z4* 3 max f4 x4
x4 3
На данном шаге величина остатка после шага 3
может принимать любое из допустимых
значений 0 3 200, а в силу требования
распределения исходных средств без остатка, то
допустимое управление принимает
единственное значение значение величины
начального состояния 4-го шага.
В свою очередь для каждого управления из
табл. 1 будем выбирать значение дохода 4-го
предприятия. Все данные соображения отразим
во вспомогательной таблице 4-го шага.
Для каждого управления, в силу уравнения
Беллмана, находим условные максимумы,
которые вместе с соответствующим им условнооптимальным управления занесем в основную
таблицу шага 4.
21
22.
240
80
120
160
200
x3
3 2 x3 f 3 x3 Z 4* 3
Z 3 3 , x3
0
40
0
4
0+4=4
40
0
3
0
3+0=3
0
80
0
6
0+6=6
40
40
3
4
3+4=7
80
0
4
0
4+0=4
0
120
0
8
0+8=8
40
80
3
6
3+6=9
80
40
4
4
4+4=8
120
0
7
0
7+0=7
0
160
0
13
0+13=13
40
120
3
8
3+8=11
80
80
4
6
4+6=10
120
40
7
4
7+4=11
160
0
11
0
11+0=11
0
200
0
16
0+16=16
40
160
3
13
3+13=16
80
120
4
8
4+8=12
120
80
7
6
7+6=13
160
40
11
4
11+4=15
200
0
18
0
18+0=18
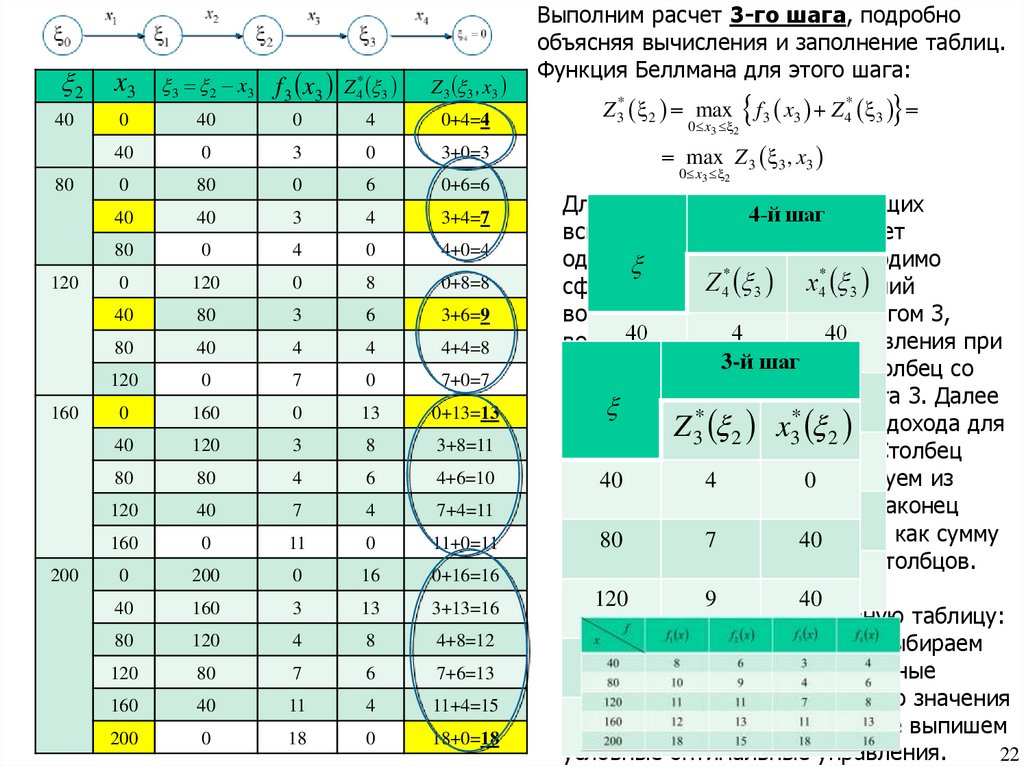
Выполним расчет 3-го шага, подробно
объясняя вычисления и заполнение таблиц.
Функция Беллмана для этого шага:
Z 3* 2 max
0 x3 2
f x Z
3
*
4
3
3
max Z 3 3 , x3
0 x3 2
Для данного шага и последующих
вспомогательная таблица имеет
одинаковую структуру: необходимо
сформировать столбцы значений
возможных остатков перед шагом 3,
возможного дискретного управления при
3-й
шаг
данном остатке,
вычислить
столбец со
значениями остатка после шага 3. Далее
*
*
формируемZстолбец
значений
дохода для
x
3 2
3 2
3-го предприятия из табл. 1. Столбец
условных
максимумов
формируем
из
40
4
0
основной таблицы шага 4. И наконец
последний
столбец
вычисляем
как сумму
80
7
40
элементов предыдущих двух столбцов.
120
9
40
На шаге 3 формируем основную таблицу:
из вспомогательной таблицы выбираем
160
13
0
максимальные значения (условные
максимумы шага 3) для каждого значения
200 перед
18шагом 3.
200А также выпишем
остатка
условные оптимальные управления.
22
23.
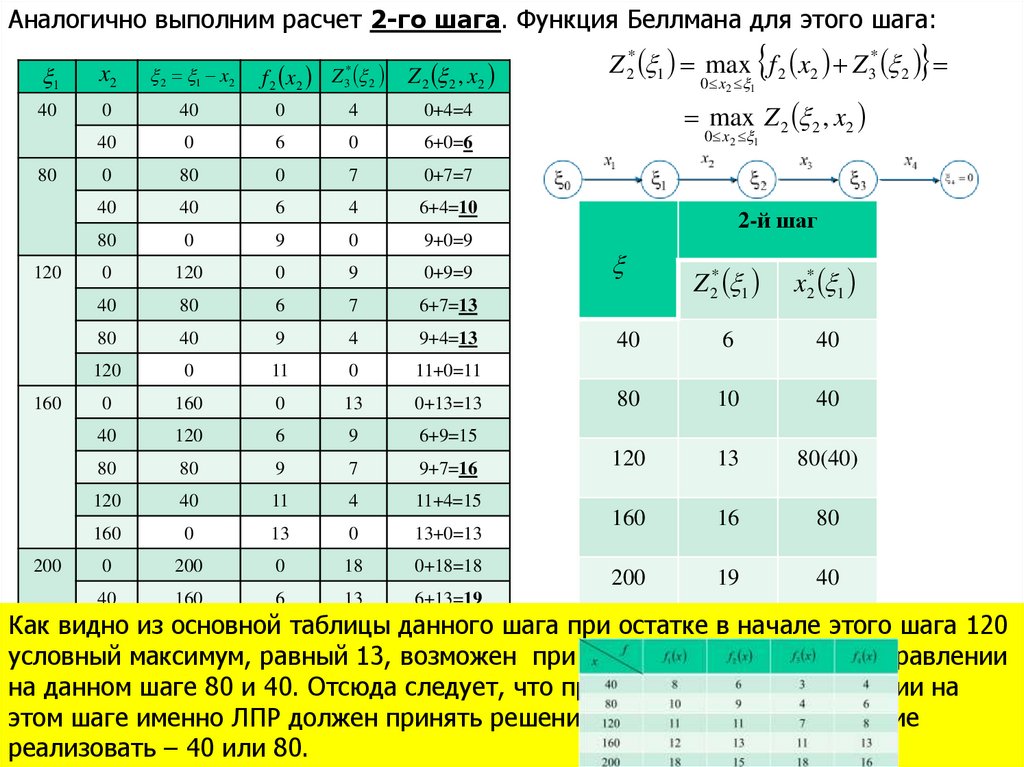
Аналогично выполним расчет 2-го шага. Функция Беллмана для этого шага:*
3
Z 2 2 , x2
f 2 x2 Z 2
1
x2
2 1 x2
40
0
40
0
4
0+4=4
40
0
6
0
6+0=6
0
80
0
7
0+7=7
40
40
6
4
6+4=10
80
0
9
0
9+0=9
0
120
0
9
0+9=9
40
80
6
7
6+7=13
80
40
9
4
9+4=13
120
0
11
0
11+0=11
0
160
0
13
0+13=13
40
120
6
9
6+9=15
80
80
9
7
9+7=16
120
40
11
4
11+4=15
160
0
13
0
13+0=13
0
200
0
18
0+18=18
40
160
6
13
6+13=19
80
120
160
200
Z 2* 1 max f 2 x2 Z 3* 2
0 x2 1
max Z 2 2 , x2
0 x2 1
2-й шаг
Z 2* 1
x2* 1
40
6
40
80
10
40
120
13
80(40)
160
16
80
200
19
40
Как видно
данного
80 из основной
120
9 таблицы
9
9+9=18 шага при остатке в начале этого шага 120
условный
равный
при условном оптимальном управлении
120 максимум,
80
11
713, возможен
11+7=18
на данном
следует,
что при безусловной оптимизации на
160 шаге
40 80 и 40.
13 Отсюда
4
13+4=17
23
этом шаге
ЛПР15должен
принять
200 именно
0
0
15+0=15 решение: какое именно управление
реализовать – 40 или 80.
24.
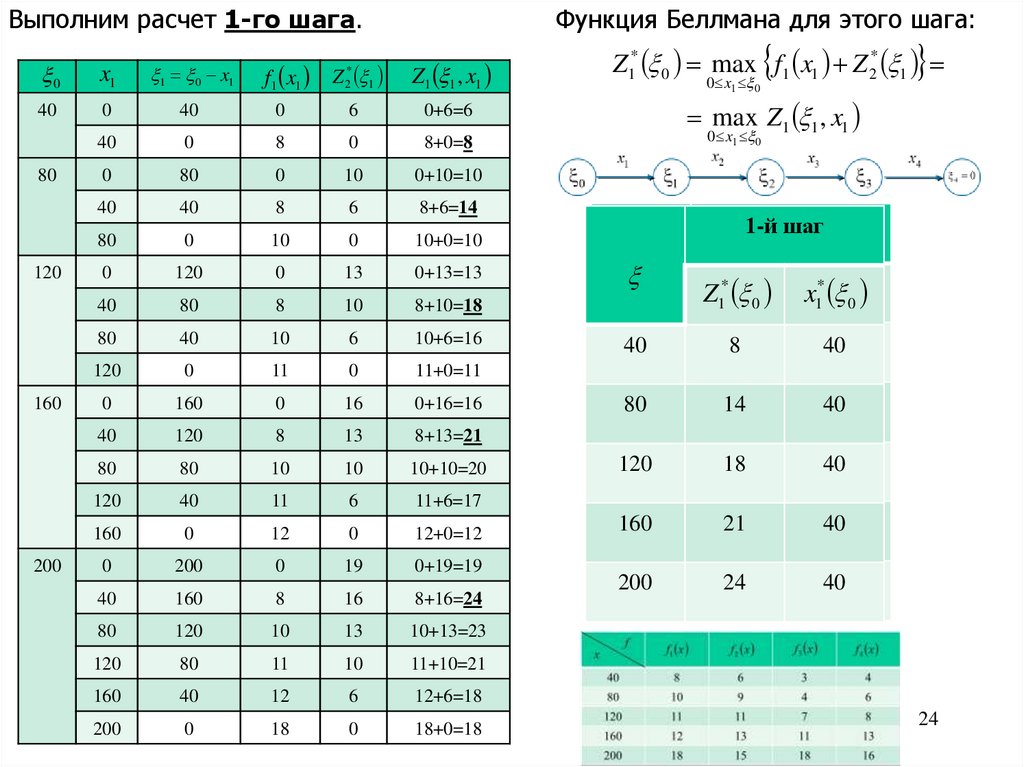
Выполним расчет 1-го шага.Функция Беллмана для этого шага:
0
x1
1 0 x1
f1 x1
Z 1
Z1 1 , x1
40
0
40
0
6
0+6=6
40
0
8
0
8+0=8
0
80
0
10
0+10=10
40
40
8
6
8+6=14
80
0
10
0
10+0=10
0
120
0
13
0+13=13
40
80
8
10
8+10=18
80
40
10
6
10+6=16
120
0
11
0
11+0=11
0
160
0
16
0+16=16
40
120
8
13
8+13=21
80
80
10
10
10+10=20
120
40
11
6
11+6=17
160
0
12
0
12+0=12
0
200
0
19
0+19=19
40
160
8
16
8+16=24
80
120
10
13
10+13=23
120
80
11
10
11+10=21
160
40
12
6
12+6=18
200
0
18
0
18+0=18
80
120
160
200
*
2
Z1* 0 max f1 x1 Z 2* 1
0 x1 0
max Z1 1 , x1
0 x1 0
1-й шаг
Z1* 0
x1* 0
40
8
40
80
14
40
120
18
40
160
21
40
200
24
40
24
25.
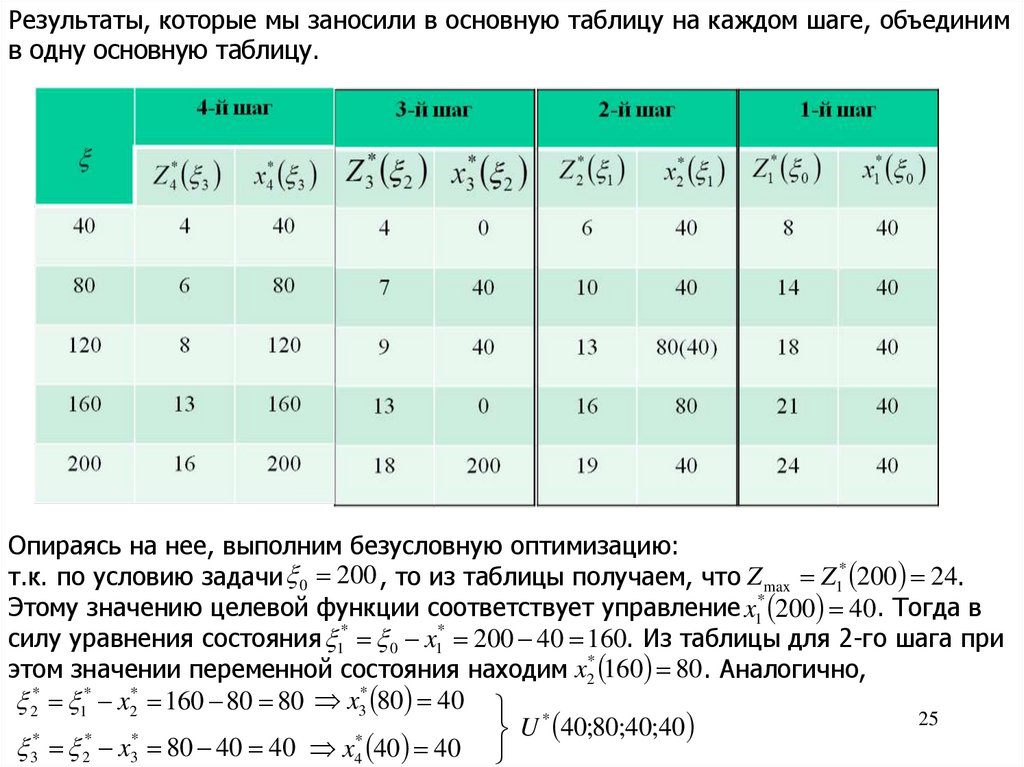
Результаты, которые мы заносили в основную таблицу на каждом шаге, объединимв одну основную таблицу.
Опираясь на нее, выполним безусловную оптимизацию:
т.к. по условию задачи 0 200 , то из таблицы получаем, что Z max Z1* 200 24.
Этому значению целевой функции соответствует управление x1* 200 40 . Тогда в
силу уравнения состояния 1* 0 x1* 200 40 160. Из таблицы для 2-го шага при
этом значении переменной состояния находим x2* 160 80 . Аналогично,
2* 1* x2* 160 80 80 x3* 80 40 *
25
U 40;80;40;40
*
*
*
*
3 2 x3 80 40 40 x4 40 40
26.
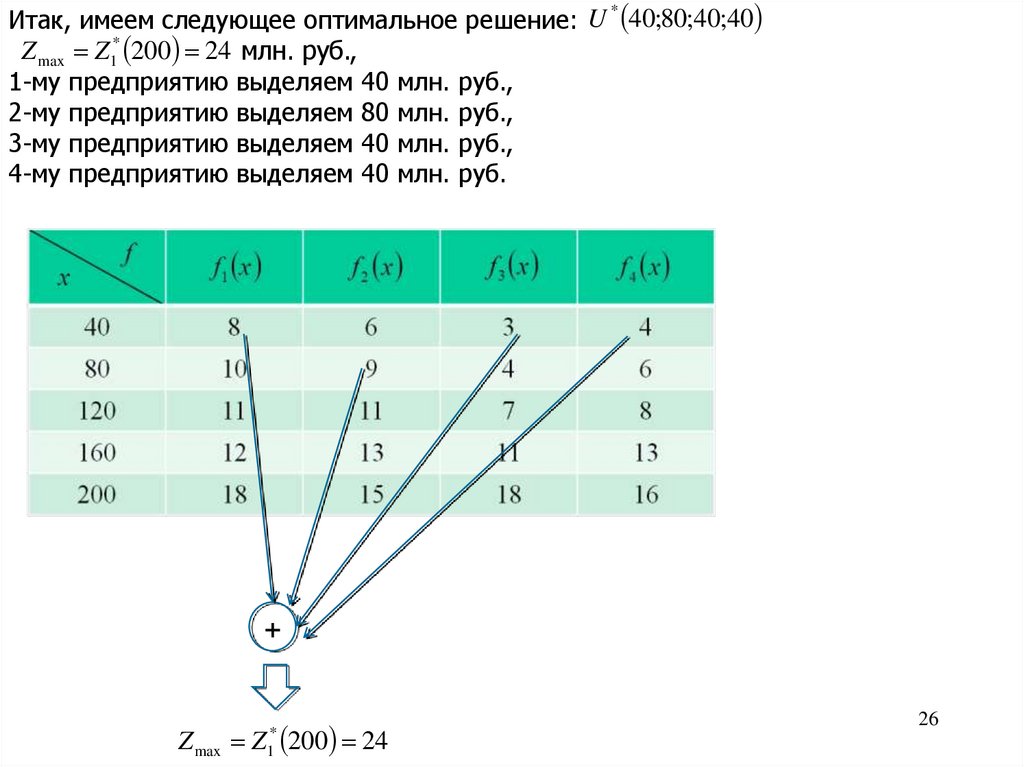
Итак, имеем следующее оптимальное решение: U 40;80;40;40Z max Z1* 200 24 млн. руб.,
1-му предприятию выделяем 40 млн. руб.,
2-му предприятию выделяем 80 млн. руб.,
3-му предприятию выделяем 40 млн. руб.,
4-му предприятию выделяем 40 млн. руб.
*
+
Z max Z 200 24
*
1
26
27.
Лекция №12Цель лекции:
– изучить задачу упорядочения.
Содержание лекции:
1. Принятие решений в задачах упорядочения
- постановка задачи
- алгоритм Джонсона
- пример
27
28.
4. Принятие решений в задачах упорядоченияЗадачи упорядочения связаны с построением расписаний, определением
оптимальной последовательности обработки изделий, массивов
информации и т.п.
Методологическую основу для решения задач упорядочения
последовательности работ предоставляет теория расписаний.
Теория расписаний – один из разделов ТПР, в котором изучаются
математические постановки и методы решения задач календарного
планирования и оперативного управления, упорядочения во времени
фиксированной системы ресурсов для выполнения определённой
совокупности работ.
При этом основное внимание уделяется вопросам оптимального
распределения и упорядочения конечного множества требований,
обслуживаемых детерминированными системами (планирование
производства, выполнение потока вычислительных задач, составление
расписания учебных занятий и т.п.).
28
29.
Рассмотрим идеализированную постановку задачиупорядочения (нахождения оптимальной последовательности)
– задача о двух машинах:
имеется m изделий, каждое из которых вначале должно быть
обработано на первой машине, а затем на второй. Известно время
обработка j-гo изделия (j = 1, 2,..., m) на первой машине t1,j и на второй
машине t2,j. Найти порядок с минимальным суммарным временем
обработки всех изделий на двух машинах.
Перечислим основные ограничения в данной задаче:
первая машина работает без простоев;
время перехода изделия от одной машины к другой незначительно,
и им можно пренебречь;
нельзя начинать обработку очередного изделия, не завершив
обработку предыдущего.
29
30.
Обозначим через tпj время простоя второй машины, если она уже свободна,а обработка очередного изделия на первой машине еще не завершена.
Тогда целевая функция, которую необходимо минимизировать, имеет вид
T t nj t 2 j min .
Задача минимизации суммарного времени обработки всех изделий на двух
машинах, по существу, сводится к минимизации суммарного времени
простоя второй машины (это справедливо лишь для двух машин!), т.к.
величина t 2 j известна:
T tnj min .
Общее число вариантов решения этой задачи равно m! Например, 5!=120.
Эту задачу можно решать методом динамического программирования.
Однако для двух машин известен эффективный алгоритм Джонсона.
Схематически процесс обработки в таких задачах удобно представлять в
виде диаграммы Ганта (далее будет проиллюстрировано на примере).
30
31.
Алгоритм Джонсона:1. Поиск минимального элемента среди всех t1,j и t2,j.
2. Перестановка изделий:
Если найденный минимальный элемент относится к первой машине, то
соответствующее j-e изделие необходимо поставить на первое место в
оптимальном упорядочении (ОУ).
Если минимальный элемент относится ко второй машине, то на последнее
место в ОУ.
Если же несколько одинаковых минимальных элементов относятся только к
1-й машине, то на первое место ставят изделие, которому соответствует
больший элемент, относящийся ко 2-й машине.
Если же несколько одинаковых минимальных элементов относятся только ко
2-й машине, то на последнее место ставят изделие, которому соответствует
больший элемент, относящийся к 1-й машине.
3. Вычёркиваем переставленные изделия и переходим к п. 1. Итерационно
повторяем алгоритм до тех пор, пока не будет исчерпан список изделий.
Примечание: при повторении пп. 1, 2 найденный текущий минимальный
элемент помещается после предыдущего, если его перемещаем в начало ОУ,
и, соответственно, перед предыдущим, если его перемещаем в конец ОУ.
31
32.
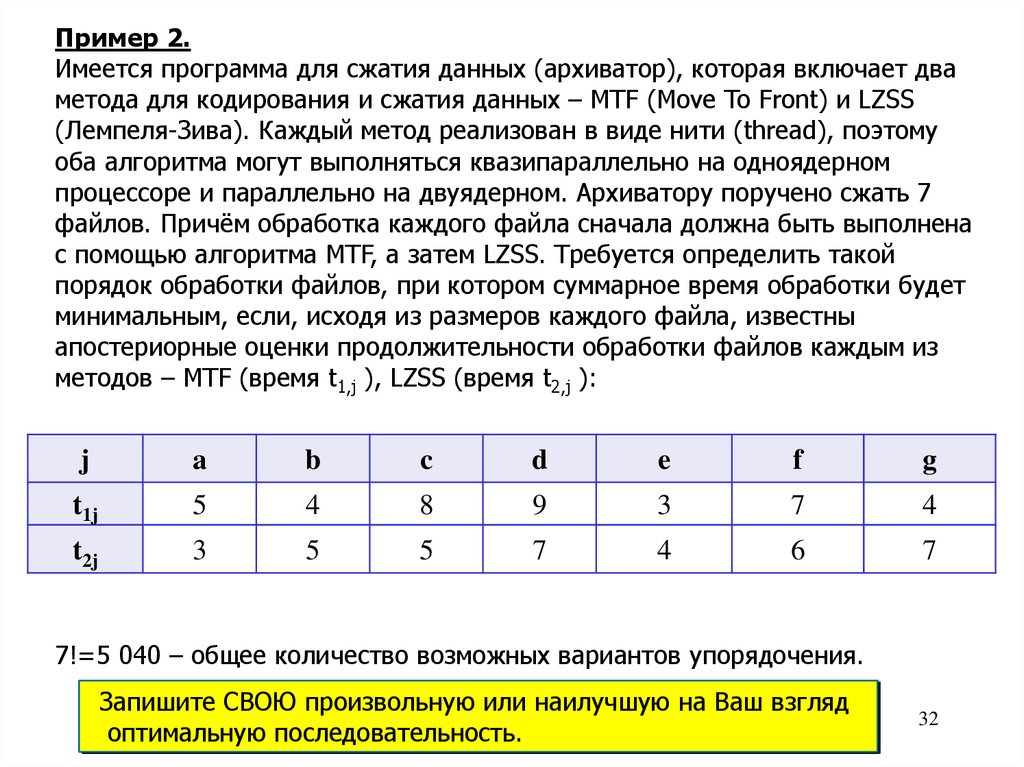
Пример 2.Имеется программа для сжатия данных (архиватор), которая включает два
метода для кодирования и сжатия данных – MTF (Move To Front) и LZSS
(Лемпеля-Зива). Каждый метод реализован в виде нити (thread), поэтому
оба алгоритма могут выполняться квазипараллельно на одноядерном
процессоре и параллельно на двуядерном. Архиватору поручено сжать 7
файлов. Причём обработка каждого файла сначала должна быть выполнена
с помощью алгоритма MTF, а затем LZSS. Требуется определить такой
порядок обработки файлов, при котором суммарное время обработки будет
минимальным, если, исходя из размеров каждого файла, известны
апостериорные оценки продолжительности обработки файлов каждым из
методов – MTF (время t1,j ), LZSS (время t2,j ):
j
a
b
c
d
e
f
g
t1j
5
4
8
9
3
7
4
t2j
3
5
5
7
4
6
7
7!=5 040 – общее количество возможных вариантов упорядочения.
Запишите СВОЮ произвольную или наилучшую на Ваш взгляд
оптимальную последовательность.
32
33.
До иллюстрации применения алгоритма Джонсона, рассмотрим некоторый вариантупорядочения (выбран произвольно), а именно: Х={a, c, f, d, e, b, g}.
Ниже показана диаграмма Ганта для данного варианта:
o на первой диаграмме показана последовательность обработки файлов
1-м методом – работы выполняются друг за другом без простоя;
o на второй диаграмме показана последовательность обработки файлов
2-м методом. Здесь уже соответствующая обработка может начинаться только
после полной обработки данного файла 1-м методом. Отсюда возникают простои
в работе 2-го метода, показанные на третьей диаграмме.
Как видим, общее время обработки всех файлов составит 37+15=52 временных
единицы, а время простоя – 15. Очевидно, что данный вариант не оптимален.
tnj 15
t2 j 37
33
34.
Рассмотрим нахождение оптимального упорядочения (ОУ) с использованиемалгоритма Джонсона:
Итерация 1
11. Ищем минимальный элемент среди всех t1,j и t2,j. Это значение 3,
соответствующее работам a и e. Как видим, они относятся к разным методам,
но выбрать необходимо одну. Выбор за ЛПР. Пусть это будет работа e.
21. Т.к. эта работа относится к 1-му методу, то эту работу помещаем в
начало ОУ. Данное решение отразим в таблице ОУ для итерации 1.
31. Вычёркиваем из исходной таблицы столбец работы e.
j
a
b
c
d
e
f
g
t1j
5
4
8
9
3
7
4
t2j
3
5
5
7
4
6
7
№ в ОУ
1
Итерация 1
e
2
3
4
5
6
7
34
35.
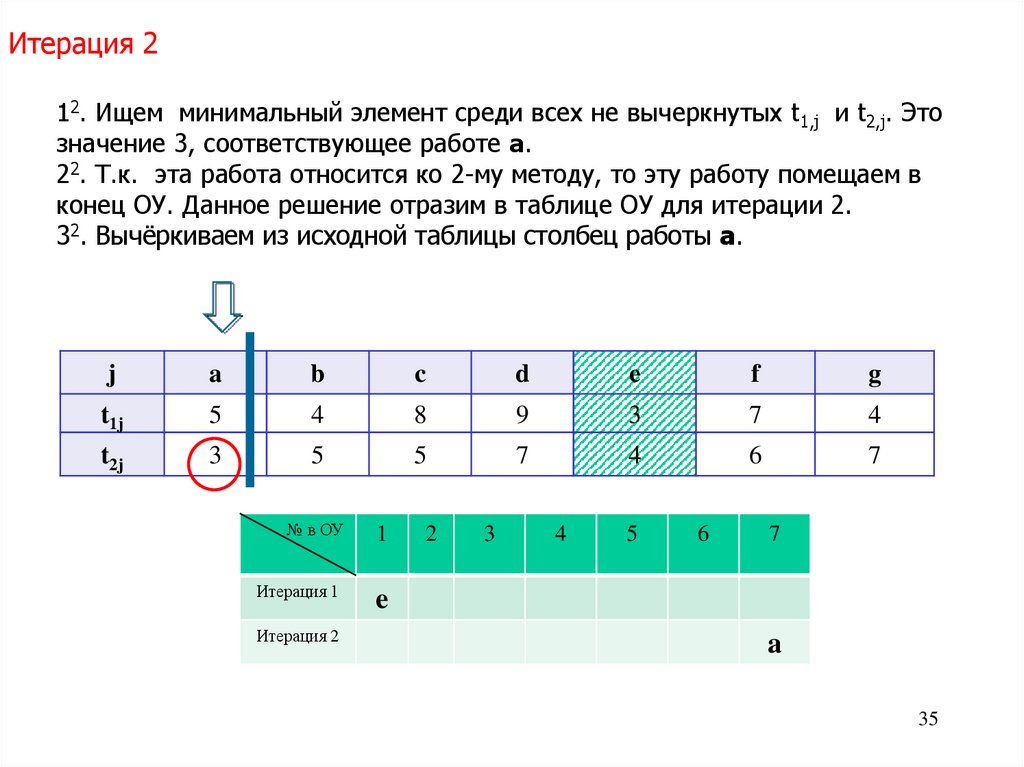
Итерация 212. Ищем минимальный элемент среди всех не вычеркнутых t1,j и t2,j. Это
значение 3, соответствующее работе a.
22. Т.к. эта работа относится ко 2-му методу, то эту работу помещаем в
конец ОУ. Данное решение отразим в таблице ОУ для итерации 2.
32. Вычёркиваем из исходной таблицы столбец работы a.
j
a
b
c
d
e
f
g
t1j
5
4
8
9
3
7
4
t2j
3
5
5
7
4
6
7
№ в ОУ
1
Итерация 1
e
Итерация 2
2
3
4
5
6
7
a
35
36.
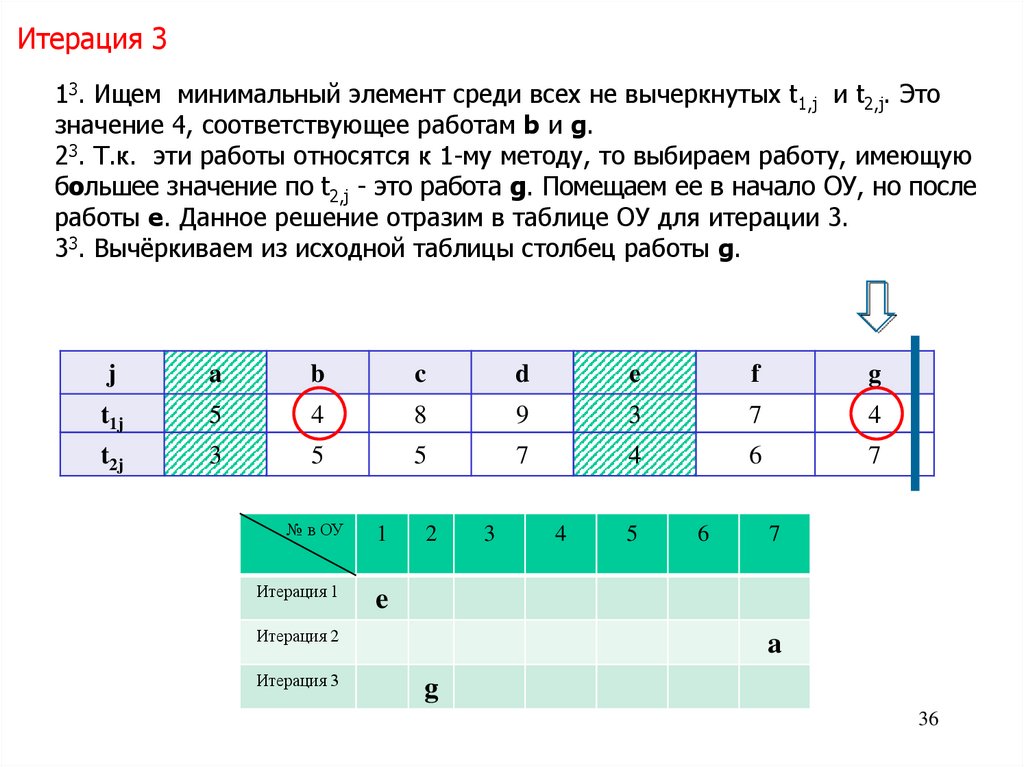
Итерация 313. Ищем минимальный элемент среди всех не вычеркнутых t1,j и t2,j. Это
значение 4, соответствующее работам b и g.
23. Т.к. эти работы относятся к 1-му методу, то выбираем работу, имеющую
большее значение по t2,j - это работа g. Помещаем ее в начало ОУ, но после
работы e. Данное решение отразим в таблице ОУ для итерации 3.
33. Вычёркиваем из исходной таблицы столбец работы g.
j
a
b
c
d
e
f
g
t1j
5
4
8
9
3
7
4
t2j
3
5
5
7
4
6
7
№ в ОУ
1
Итерация 1
e
2
Итерация 2
Итерация 3
3
4
5
6
7
a
g
36
37.
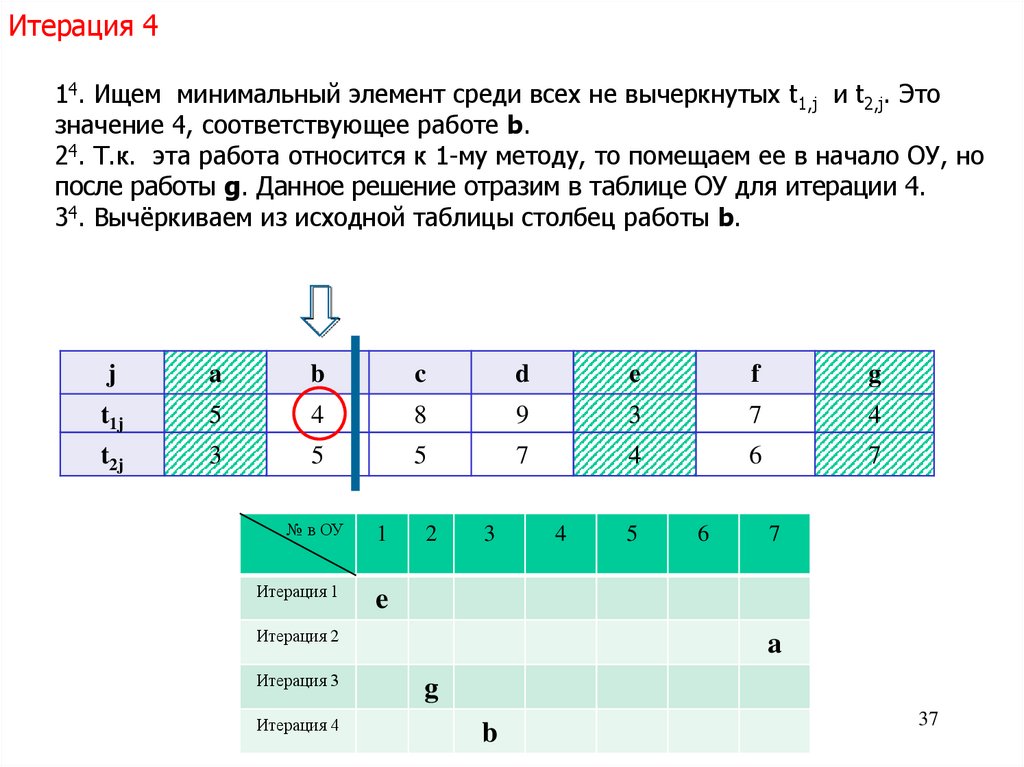
Итерация 414. Ищем минимальный элемент среди всех не вычеркнутых t1,j и t2,j. Это
значение 4, соответствующее работе b.
24. Т.к. эта работа относится к 1-му методу, то помещаем ее в начало ОУ, но
после работы g. Данное решение отразим в таблице ОУ для итерации 4.
34. Вычёркиваем из исходной таблицы столбец работы b.
j
a
b
c
d
e
f
g
t1j
5
4
8
9
3
7
4
t2j
3
5
5
7
4
6
7
№ в ОУ
1
Итерация 1
e
2
3
Итерация 2
Итерация 3
Итерация 4
4
5
6
7
a
g
b
37
38.
Итерация 515. Ищем минимальный элемент среди всех не вычеркнутых t1,j и t2,j. Это
значение 5, соответствующее работе c.
25. Т.к. эта работа относится ко 2-му методу, то помещаем ее в конец ОУ, но
перед работой a. Данное решение отразим в таблице ОУ для итерации 5.
35. Вычёркиваем из исходной таблицы столбец работы c.
j
a
b
c
d
e
f
g
t1j
5
4
8
9
3
7
4
t2j
3
5
5
7
4
6
7
№ в ОУ
1
Итерация 1
e
2
3
4
5
6
Итерация 2
Итерация 3
Итерация 4
Итерация 5
7
a
g
b
c
38
39.
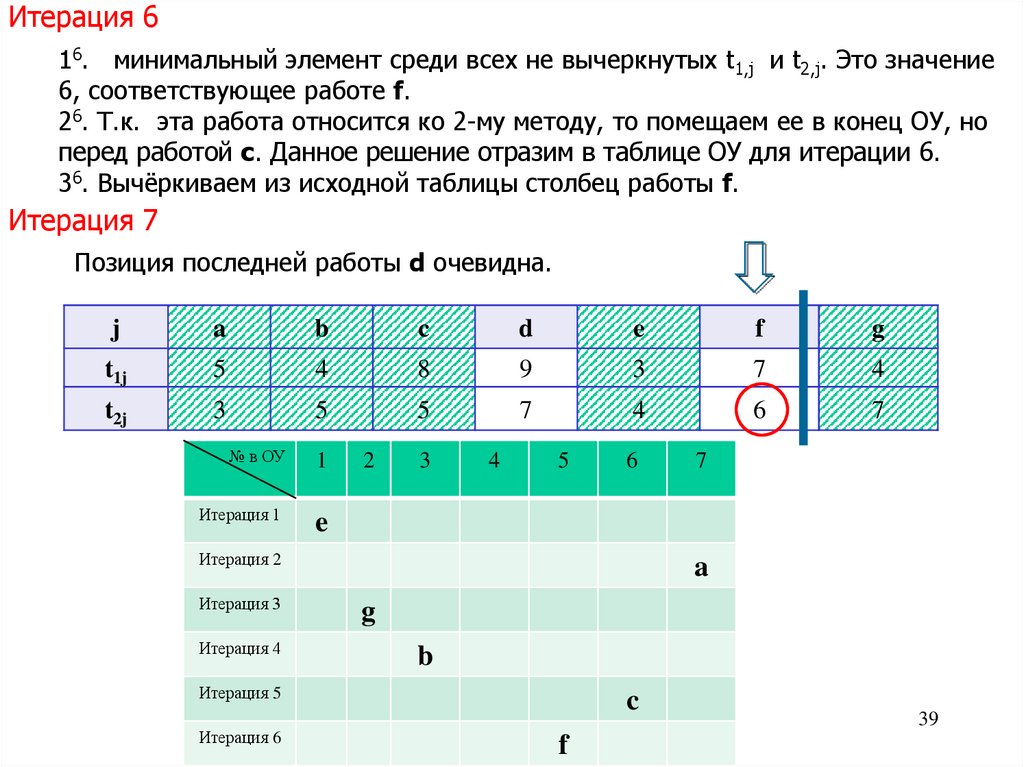
Итерация 616. минимальный элемент среди всех не вычеркнутых t1,j и t2,j. Это значение
6, соответствующее работе f.
26. Т.к. эта работа относится ко 2-му методу, то помещаем ее в конец ОУ, но
перед работой c. Данное решение отразим в таблице ОУ для итерации 6.
36. Вычёркиваем из исходной таблицы столбец работы f.
Итерация 7
Позиция последней работы d очевидна.
j
a
b
c
d
e
f
g
t1j
5
4
8
9
3
7
4
t2j
3
5
5
7
4
6
7
№ в ОУ
1
Итерация 1
e
2
3
4
5
6
Итерация 2
Итерация 3
Итерация 4
a
g
b
Итерация 5
Итерация 6
7
c
f
39
40.
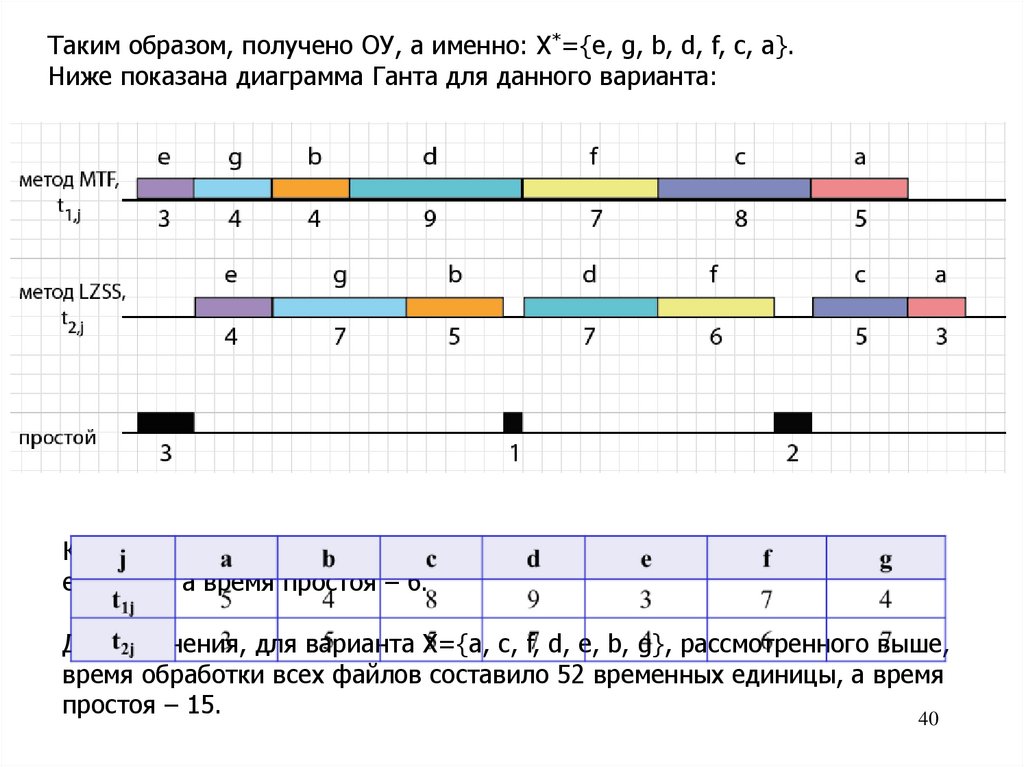
Таким образом, получено ОУ, а именно: Х*={e, g, b, d, f, c, a}.Ниже показана диаграмма Ганта для данного варианта:
Как видим, общее время обработки всех файлов составит 43 временных
единицы, а время простоя – 6.
Для сравнения, для варианта Х={a, c, f, d, e, b, g}, рассмотренного выше,
время обработки всех файлов составило 52 временных единицы, а время
простоя – 15.
40
41.
Алгоритм Джонсона можно применить для трёх машин лишь при соблюденииодного из следующих двух неравенств:
1) min {t1j } ≥ max {t2j } (если при заданном технологическом порядке
обработки изделий данное условие выполняется, то суммируются t1j и t2j ,
и задача сводится к двум машинам);
2) min {t3j} ≥ max {t2j } (если при заданном технологическом порядке
обработки изделий данное условие выполняется, то суммируются t2j и t3j ,
и задача сводится к двум машинам).
К достоинствам алгоритма Джонсона можно отнести возможность нахождения
оптимальной последовательности обработки за один проход алгоритма, а
многовариантность перестановок (при совпадении минимальных элементов) в
конечном счёте не оказывает влияния на значение целевой функции.
В сравнении с алгоритмами Гомори, ветвей и границ или динамическим
программированием алгоритм Джонсона имеет заметное преимущество во
времени нахождения оптимальной последовательности, однако область его
применения ограничена двумя машинами.
41

























 Математика
Математика








