Похожие презентации:
Критерии для принятия решений. Теория игр
1.
Критерии дляпринятия
решений
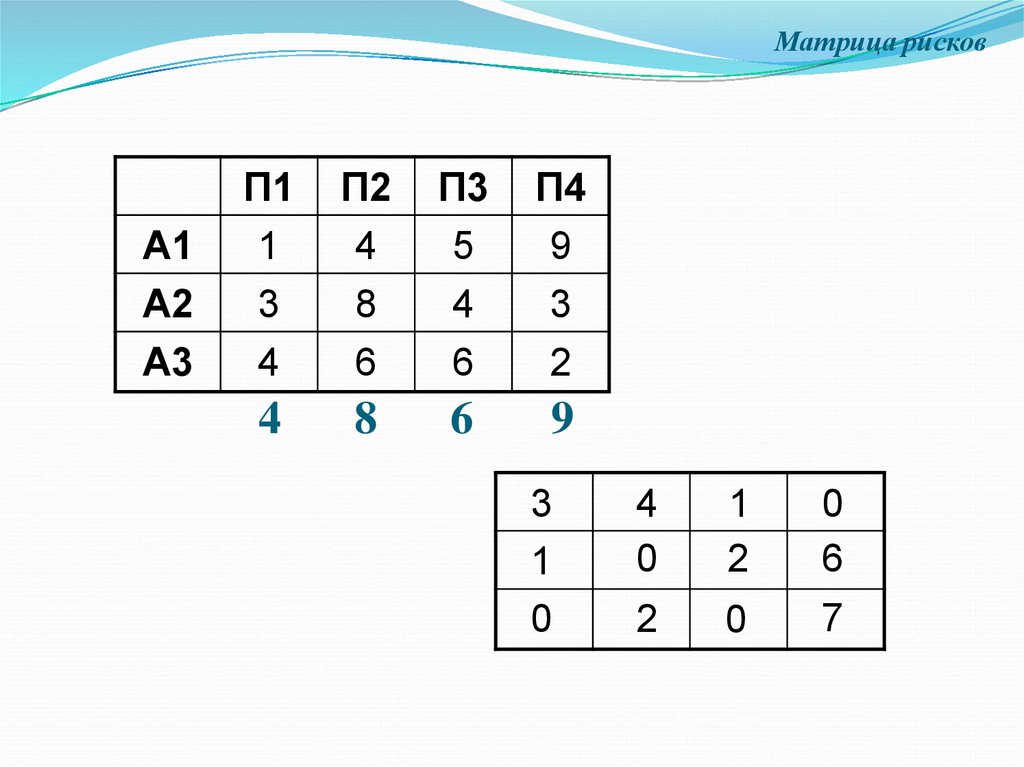
2. Матрица рисков
Пример: Планируется операция в заранее неясныхусловиях, касающихся, например, рыночной
конъюнктуры. Относительно этих условий можно
сделать предположения: П1, П2, П3, П4. Выгодность
операции (ожидаемая прибыль) при наших стратегиях
Аi для разных условий Пj задана матрицей (aij)
выигрышей:
A1
A2
A3
П1
1
3
4
П2
4
8
6
П3
5
4
6
П4
9
3
2
Построим матрицу рисков.
3. Матрица рисков
A1A2
A3
П1
1
3
4
П2
4
8
6
П3
5
4
6
П4
9
3
2
4
8
6
9
3
1
0
4
0
1
2
2
0
0
6
7
4.
Матрица рисковn
Средний риск r i Q j rij min
j 1
n
n
n
a i r i Q j a ij Q j j a ij Q j j = c - const
j 1
j 1
j 1
Средний риск
r i min
т.т.т.
r i c ai
a i max
5. Критерий Лапласа
Критерии для принятия решенийКритерий Лапласа
П1, П2, П3, П4. Выгодность операции (ожидаемая
прибыль) при наших стратегиях Аi для разных
условий Пj задана матрицей (aij) выигрышей:
Q1 P(П1), ..., Qn P(Пn )
n
Q j 1
j 1
n
a i Mi Q1 a i1 ... Q n a in Q a
j ij
j 1
Нужно выбрать ту из стратегий Ai, для которой a i max
6. Максиминный критерий Вальда
Критерии для принятия решенийМаксиминный критерий Вальда
W max min a ij
j
i
«Всегда надо рассчитывать на худшее!»
Критерий минимаксного риска Сэвиджа
S min max rij
i
j
«Любыми путями избежать большого
риска при принятии решения!»
7.
Критерии для принятия решенийКритерий пессимизма-оптимизма
Гурвица
H max min a ij (1 ) max a ij
j
i
j
0 1
1
H max min a ij
j
i
0
H max max a ij - критерий «крайнего
i
j
оптимизма»
- критерий Вальда
8. Оптимальный вариант электростанции
В данном регионе имеются возможности:A1 - построение большого водохранилища и
гидроэлектростанции;
A2 - сооружение тепловой электростанции на основном
(газовом) топливе и резервном (мазуте);
A3 - сооружение атомной электростанции.
Возможные решения А = {A1, A2, A3}.
Экономическая эффективность каждого варианта
рассчитана проектным институтом, который учитывал
затраты на строительство и эксплуатационные
расходы.
9. Оптимальный вариант электростанции
На эксплуатационные расходы гидроэлектростанциивлияют климатические условия, например, такие, как
погодные условия, определяющие уровень воды в
водохранилищах.
Большое число случайных факторов воздействует на
экономическую эффективность тепловой станции: цены на
мазут и газ, срывы поставок мазута из-за неритмичности
работы транспорта в зимнее время, особенно во время
снегопадов и продолжительных морозов.
Экономическая эффективность атомной электростанции
будет зависеть от больших затрат на строительство и
устойчивости агрегатов и системы управления во время
эксплуатации.
10.
Оптимальный вариант электростанцииТаким образом, погодные условия будут в основном
сказываться на расходах по эксплуатации
гидроэлектростанции и тепловой электростанции.
Следовательно, на эффективность тепловой
электростанции будут влиять как погодные условия,
так и цены на газ и мазут.
11.
Оптимальный вариант электростанцииСлучайные факторы, от которых зависит экономическая
эффективность вариантов капиталовложении,
объединим в четыре возможных состояния природы W = (Q1, Q2, Q3, Q4) с учетом окупаемости:
Q1 - цены на газ и мазут низкие и климатические
условия благоприятные;
Q2 - цены на газ и мазут высокие и климатические
условия благоприятные;
Q3 - цены на газ и мазут низкие и климатические
условия неблагоприятные;
Q4 - цены на газ и мазут высокие и климатические
условия неблагоприятные.
12.
Оптимальный вариант электростанцииПредставим в таблице полученные расчеты
эффективности W(Q, A).
A1
A2
A3
Q1
50
40
30
Q2
50
25
30
Q3
25
35
30
Q4
25
20
30
По данным многолетней статистики цен и состояний
получены оценки апостериорного (получены после опыта)
распределения состояний природы:
P(Q1) = 0,15; P(Q2) = 0,3; Р(Q3) = 0,2; P(Q4) = 0,35
Задача. Необходимо построить в регионе электростанцию
большой мощности.
13.
Оптимальный вариант электростанцииQ1 Q2 Q3 Q4
A1 50 50 25 25
A2 40 25 35 20
A3 30 30 30 30
P(Q1) = 0,15;
Р(Q3) = 0,2;
P(Q2) = 0,3;
P(Q4) = 0,35.
М(А1) = 50*0,15 + 50*0,3 + 25*0,2 + 25*0,35 = 36,25;
М(А2) = 40*0,15 + 25*0,3 + 35*0,2 + 20*0,35 = 27,5;
М(А3) = 30*0,15+30*0,3+30*0,2+30*0,35=30.
max M(Ai) = M(A1) = 36,25
A1 - построение гидроэлектростанции
14. Оптимальный вариант электростанции
Упражнение: Найти оптимальный вариантэлектростанции, если дана таблица эффективностей:
10 8 4
9 9 5
8 10 3
7 7 8
11
10
14
12













 Математика
Математика Экономика
Экономика








