Метод анализа иерархий

1.

Метод анализа
иерархий
Ситуации использования, особенности
реализации, примеры применения….

2.

В практике управления случается так, что
руководитель в точности знает результат каждого из
альтернативных вариантов выбора. Известно все об
объектах выбора, их оценках по различным критериям,
возможных состояниях сущности явлений, влияющих
на решение. Лицо, принимающее решение, «просто»
выбирает стратегию, направление действий или проект,
которые дадут максимальную отдачу.

3.

Сложность самой ситуации принятия решения
при этом объясняется большим числом
альтернатив и критериев их оценки. Чтобы не
пропустить ни одного варианта и адекватно
оценить каждый из них по каждому из критериев,
и полезен Метод анализа иерархий (МАИ). МАИ
относится к классу т.н. критериальных методов.
Он получил широкое распространение и до сих
пор активно используется в управленческой
практике. Его использование приводит ЛПР к
варианту, наилучшим образом согласующемуся
с его видением ситуации и представлениями о
наилучшем решении.

4.

Метод анализа иерархий
Это математический инструмент принятия
решений, который не «предписывает» какоголибо «правильного» решения, а указывает на тот
вариант,
который
наилучшим
образом
согласуется с пониманием сути проблемы
(варианты) и требованиями к ее решению
(критерии).

5.

Автор метода: Томас Саати
(1926-2017), американский
математик, профессор Школы
бизнеса Каца, Пенсильванского
и Питсбургского
университетов. Разработал в
1970 г. метод "Аналитической
иерархической процедуры«
или «Метод анализа
иерархий», известный в
России также как "Иерархия
Саати". Его метод основан на
построении и анализе т.н.
матриц попарных сравнений.

6.

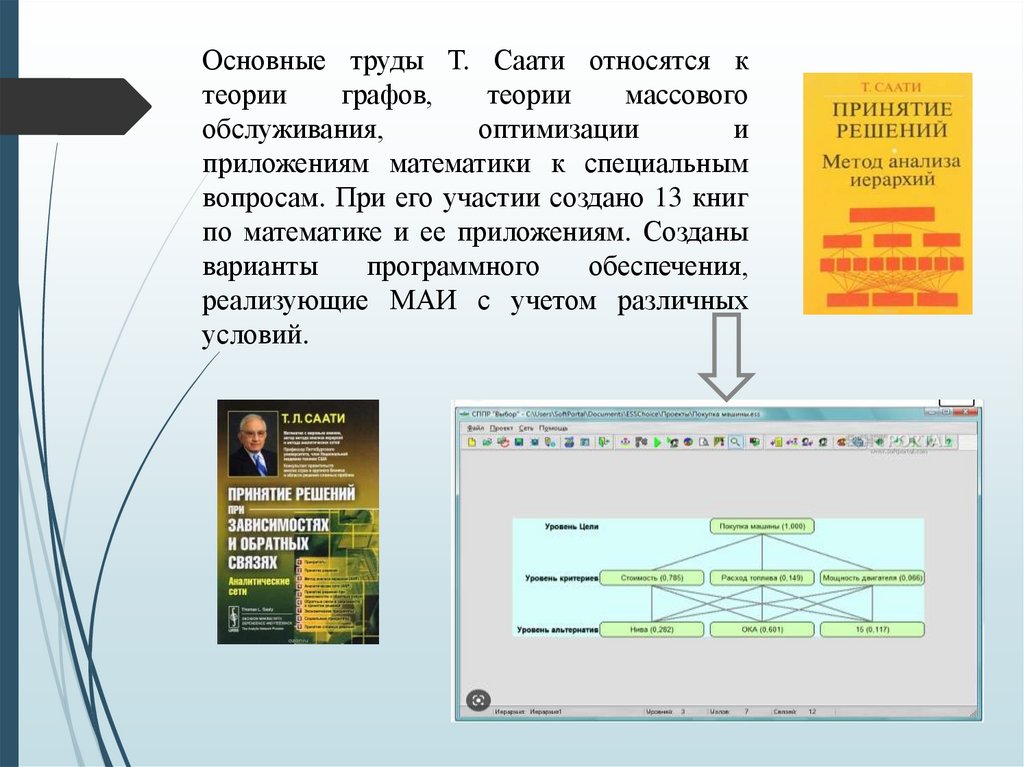
Основные труды Т. Саати относятся к
теории
графов,
теории
массового
обслуживания,
оптимизации
и
приложениям математики к специальным
вопросам. При его участии создано 13 книг
по математике и ее приложениям. Созданы
варианты
программного
обеспечения,
реализующие МАИ с учетом различных
условий.

7.

Цель метода анализа иерархий –
Количественное обоснование выбора наилучшей из
предлагаемых альтернатив, характеристики которых
являются разнородными, в том числе - и с нечетко
определенными компонентами.

8.

Технически суть метода анализа иерархий
сводится
к
поэтапному
решению
следующих
взаимосвязанных
частных
задач:
- построение иерархической структуры
показателей (признаков);
- оценивание значимости отдельных
частных показателей для каждого уровня
иерархии;
- сравнение имеющихся альтернатив и
выбор наилучшей из них.

9.

Примеры ситуаций, когда успешно
«работает» МАИ:
-выбор кандидата на должность;
-отбор лучшего проекта из многих;
-выбор покупаемого объекта (квартиры,
подарка, автомобиля и т.д);
-выбор способа вложения денег;
-выбор работы, вуза, поликлиники…
Общее: объектов много, мы многое (почти все) о
них знаем и многого от них хотим, желая не
пропустить ни одного нюанса при выборе.

10.

ПРИМЕРЫ
СИТУАЦИЙ

11.

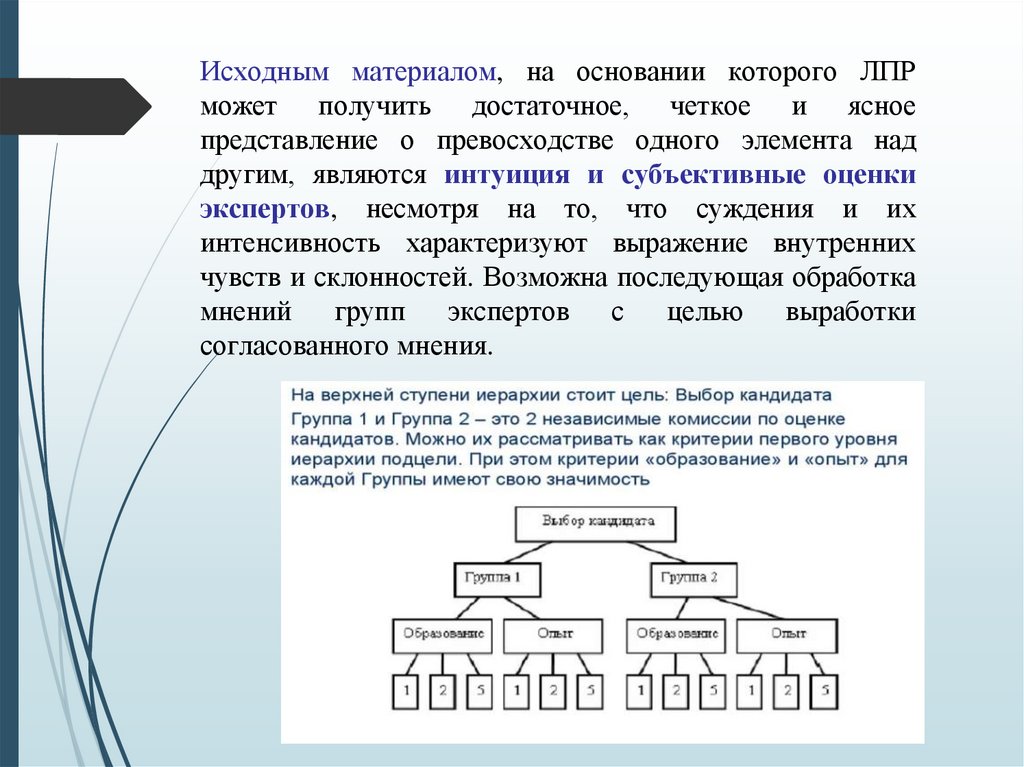
Исходным материалом, на основании которого ЛПР
может получить достаточное, четкое и ясное
представление о превосходстве одного элемента над
другим, являются интуиция и субъективные оценки
экспертов, несмотря на то, что суждения и их
интенсивность характеризуют выражение внутренних
чувств и склонностей. Возможна последующая обработка
мнений групп экспертов с целью выработки
согласованного мнения.

12.

Замечание. Мы ограничимся рассмотрением более простого
варианта МАИ, в котором оценки сделаны по ранговым шкалам.

13.

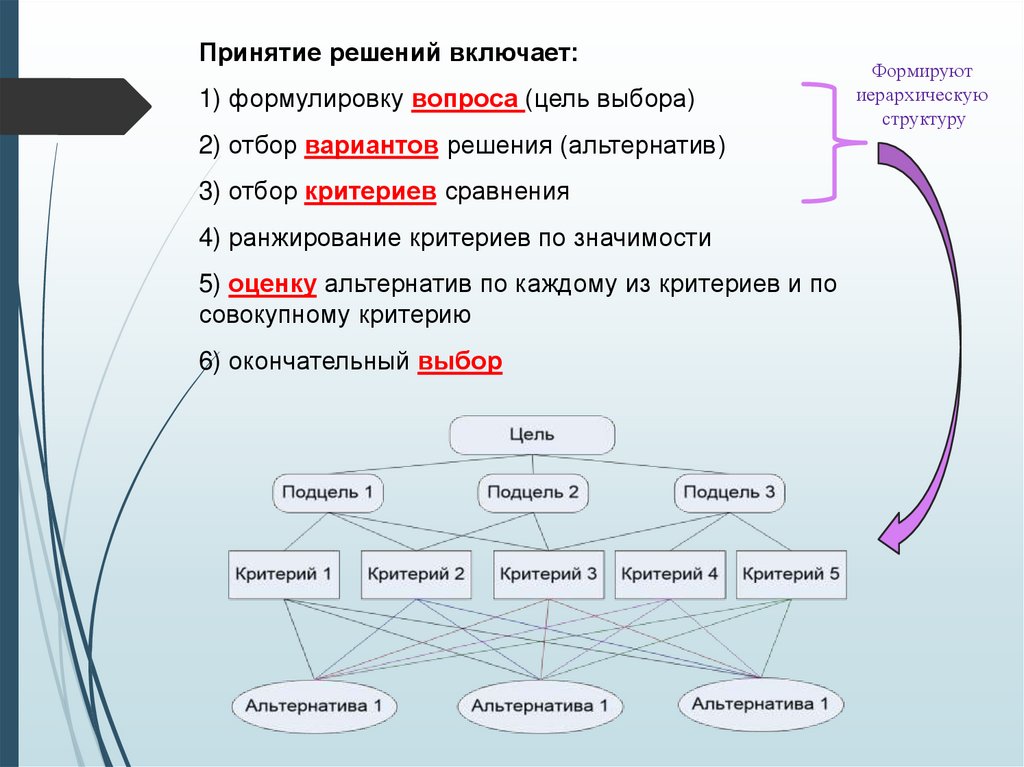
Принятие решений включает:
1) формулировку вопроса (цель выбора)
2) отбор вариантов решения (альтернатив)
3) отбор критериев сравнения
4) ранжирование критериев по значимости
5) оценку альтернатив по каждому из критериев и по
совокупному критерию
6) окончательный выбор
Формируют
иерархическую
структуру

14.

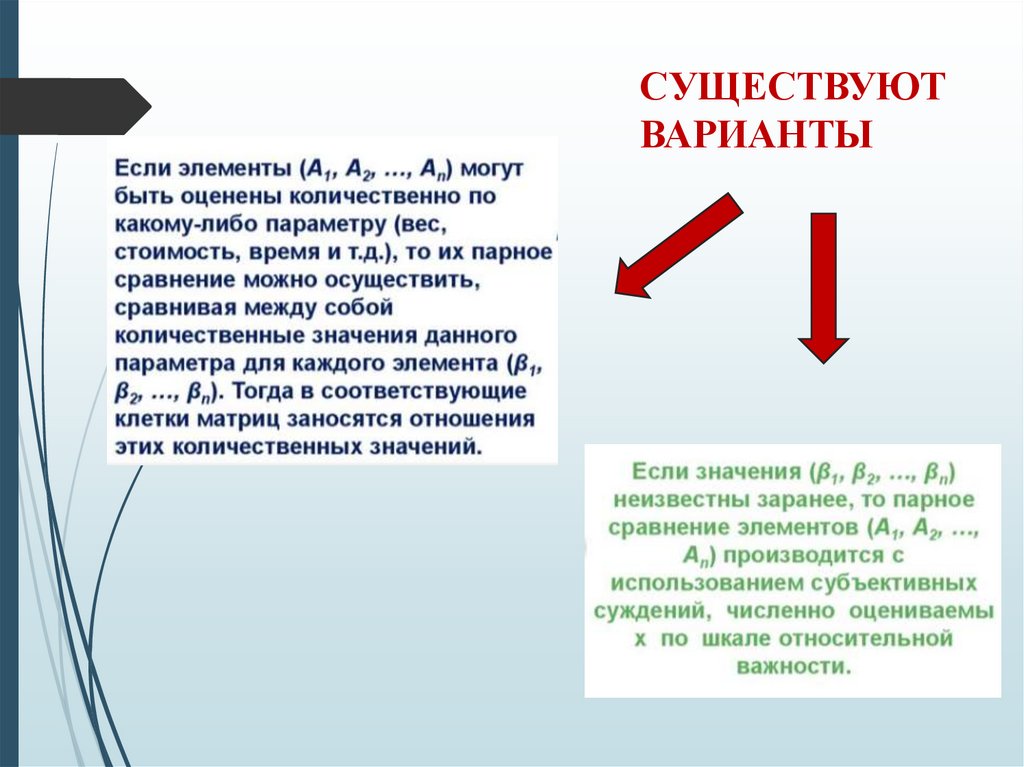
СУЩЕСТВУЮТ
ВАРИАНТЫ

15.

При попарном сравнении альтернатив можно
пользоваться, например,
упрощенной шкалой от 1 до 3.
Если требуется сравнить альтернативу1 и
альтернативу2, то возможны след. варианты:
1/1 – альтернатива1 и альтернатива2 равнозначны
2/1 – альтернатива1 лучше альтернативы2
1/2 – альтернатива1 хуже альтернативы2
3/1 – альтернатива1 существенно лучше
альтернативы2
1/3 – альтернатива1 существенно хуже
альтернативы2

16.

17.

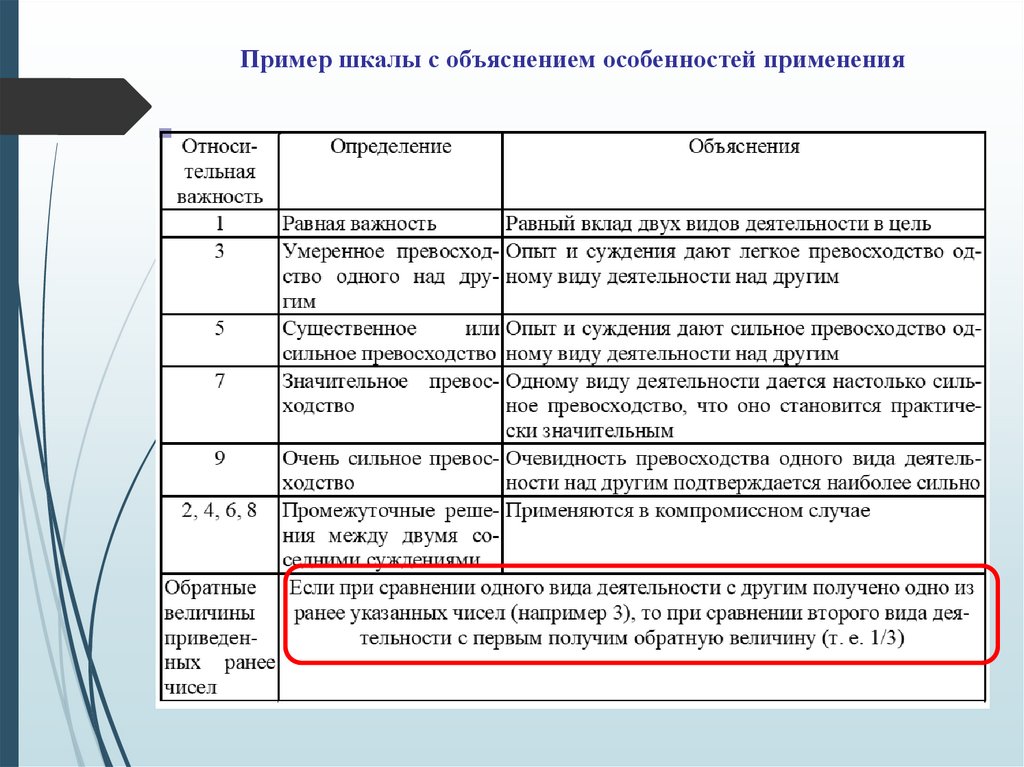
Пример шкалы с объяснением особенностей применения

18.

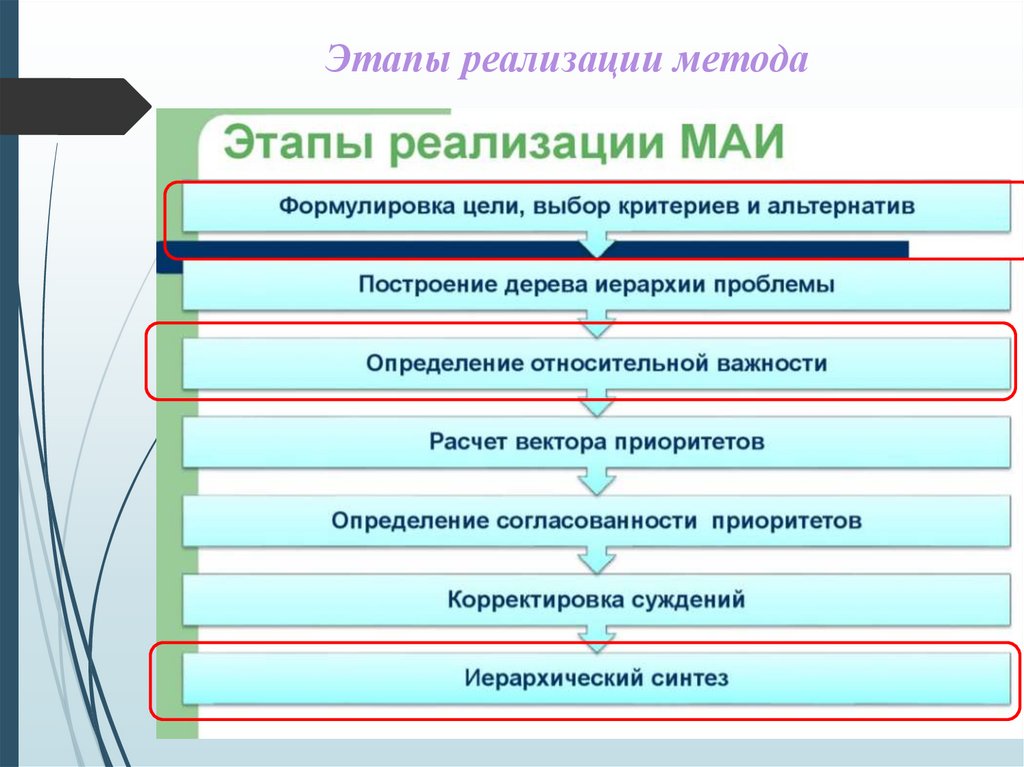
Этапы реализации метода

19.

Если проще:
1) Постановка цели.
2) Определение объектов для выбора и
составление перечня критериев их оценки.
3) Применение процедуры попарных
сравнений для оценки критериев, а также
для сравнения альтернатив по каждому из
критериев (заполнение множества матриц).
4) Получение общей оценки каждой
альтернативы по всем критериям (например,
как «взвешенной» суммарной оценки).
5) Сравнение оценок и окончательный выбор.

20.

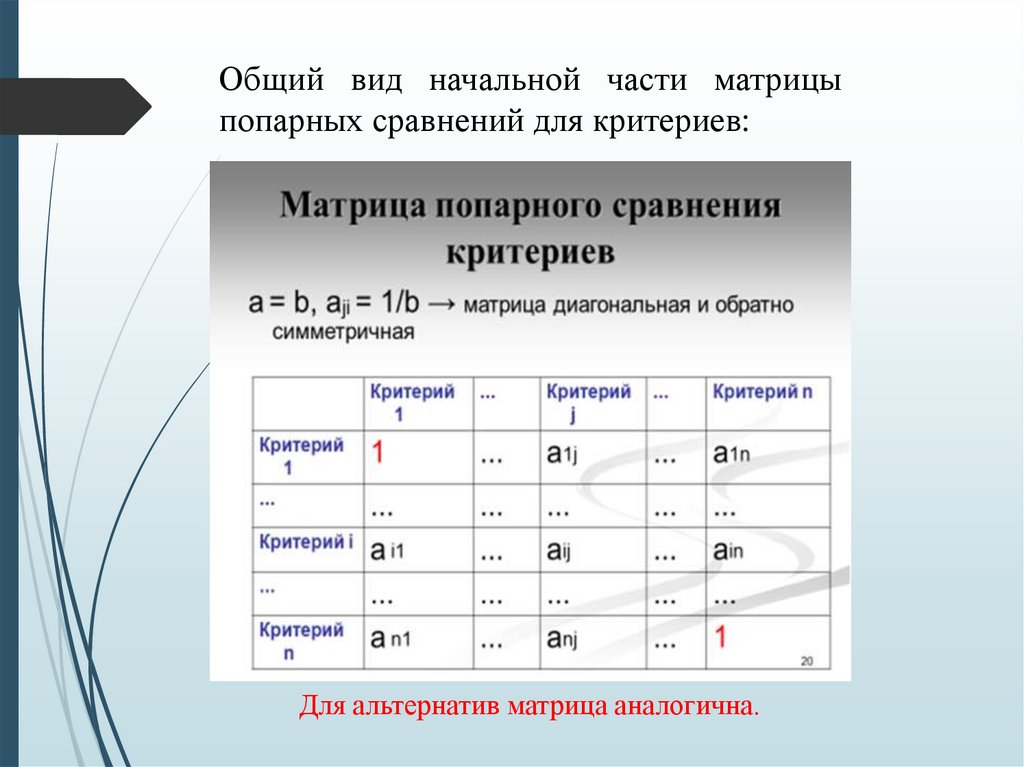
Общий вид начальной части матрицы
попарных сравнений для критериев:
Для альтернатив матрица аналогична.

21.

Нормирование
компонент
матриц попарных сравнений
осуществляется путем деления
каждой компоненты ее столбца
на сумму всех компонент этого
столбца.

22.

23.

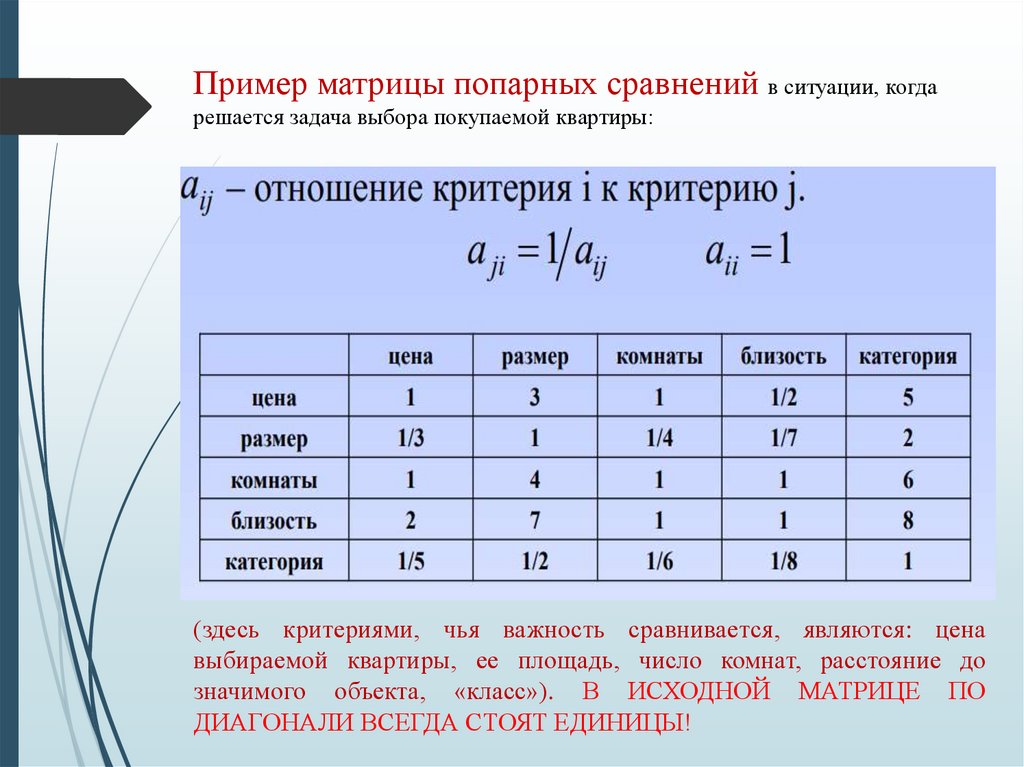
Пример матрицы попарных сравнений в ситуации, когда
решается задача выбора покупаемой квартиры:
(здесь критериями, чья важность сравнивается, являются: цена
выбираемой квартиры, ее площадь, число комнат, расстояние до
значимого объекта, «класс»). В ИСХОДНОЙ МАТРИЦЕ ПО
ДИАГОНАЛИ ВСЕГДА СТОЯТ ЕДИНИЦЫ!

24.

Замечание. В контрольной работе будем пользоваться
нижней формулой.

25.

Похожим образом заполняются остальные
таблицы,
связанные
со
сравнением
альтернатив между собой по каждому из
критериев. При большом числе критериев
возможно объединение их в группы и
сравнение групп. В последней таблице для
окончательного
выбора
нужно
«соединить»
(перемножить)
будет
оценки
альтернатив по каждому из критериев и веса
соответствующих критериев.

26.

Зачем объединять критерии в группы?
Критериев может быть много, и возможны
зависимые критерии; группы можно (полезно)
оценить по важности; для быстроты можно
ограничиться оценкой по самой значимой
группе или рассмотрением альтернатив с
высокими оценками именно по этой группе.

27.

Пример формализации ситуации:
необходимо выбрать подарок на Новый год, если
Решения (могу купить):
1) недорогой гаджет (фоторамка и т.п.)
2) билеты на любимого артиста
3) набор для хобби
4) модный аксессуар
Критерии (хочу достичь):
1) сделать сюрприз
2) принести пользу
3) сэкономить в стоимости подарка

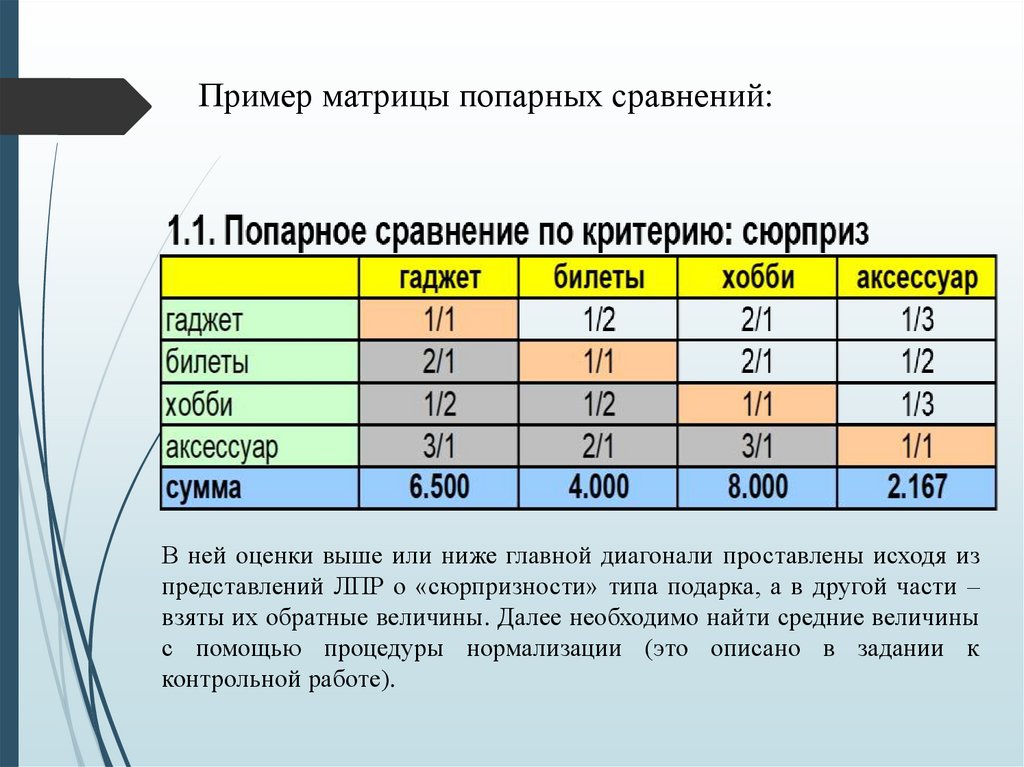
28.

Пример матрицы попарных сравнений:
В ней оценки выше или ниже главной диагонали проставлены исходя из
представлений ЛПР о «сюрпризности» типа подарка, а в другой части –
взяты их обратные величины. Далее необходимо найти средние величины
с помощью процедуры нормализации (это описано в задании к
контрольной работе).

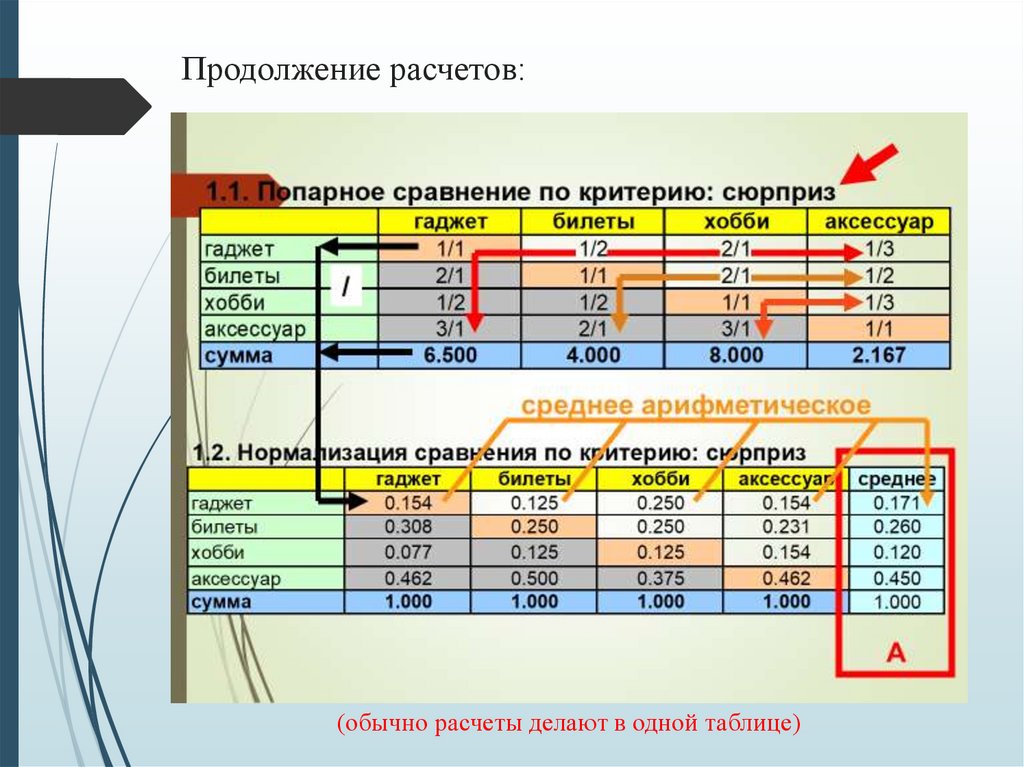
29.

Продолжение расчетов:
(обычно расчеты делают в одной таблице)

30.

31.

Основным достоинством метода анализа
иерархий
является
его
высокая
универсальность. Метод может применяться
для решения самых разнообразных задач:
анализа возможных сценариев развития
ситуации,
распределения
ресурсов,
составления рейтинга клиентов, принятия
кадровых
решений,
выбора
сложной
технической конструкции из многих похожих и
т.д. Кроме того, реализацию метода
достаточно просто автоматизировать.

32.

Недостатком
МАИ
является
необходимость получения и обработки
большого объема информации (особенно,
если решение принимают несколько
экспертов, и нужно согласовать их мнения),
требует временных затрат. Также можно
сказать, что некоторые оценки альтернатив
по критериям и самих критериев по
важности могут быть весьма субъективны.

33.

Замечание.
Вместе
(одновременно)
с
получением матриц парных сравнений иногда
необходимо
провести
оценки
степени
отклонения от согласованности (для чего
вводятся
индексы
согласованности,
вычисляемые с нахождением собственных
значений матриц сравнений).
В случае несогласованности для различных
матриц, для которых такие отклонения
превышают установленные пределы, эксперту
следует перепроверить суждения, отраженные
в матрице. Для улучшения согласованности
следует
использовать
дополнительную
информацию или пересмотреть исходные
суждения.

34.

Индекс
согласованности
–
количественная
оценка
противоречивости результатов сравнений (для системы в
целом, для узлов одного кластера – критериев или
альтернатив). Следует иметь в виду, что между
достоверностью и непротиворечивостью сравнений нет явной
связи. Противоречия в сравнениях возникают из-за
субъективных ошибок экспертов. Индекс согласованности не
зависит от шкал сравнений, но зависит от количества парных
сравнений. Индекс согласованности – положительное число.
Чем меньше противоречий в сравнениях, тем меньше значение
индекса согласованности. При использовании способа
сравнений с эталоном значение индекса согласованности
равно нулю. Достоверность результата сравнения –
количественной оценка, характеризующая степень неточности
(размытости)
результата
сравнения,
связанная
с
компетентностью эксперта, уровнем доверия к данным и т.п.
Она выражается долей единицы (или в %). Нулю
соответствуют абсолютно недостоверные сравнения, единице
(или 100%) – абсолютно достоверные сравнения.

35.

Показатели согласованности и достоверности для
системы в целом, характеризующие качество
данных, использованных для вычисления векторов
приоритетов, также являются результатами.
Величины этих показателей позволяют оценить
степень доверия к результатам, полученным с
помощью метода анализа иерархий. Знание
показателей согласованности позволяет решать
промежуточную задачу выявления участков
проблемы, по которым имеется наиболее
противоречивая информация. Решение такой задачи
позволяет сделать сбор и корректировку данных
более целенаправленными.

36.

Сам Т. Саати считал целесообразным
оценивать не более 7±2 составляющих
(критериев, альтернатив) на каждом уровне.
При применении метода следует иметь в
виду, что, как отмечает Саати, "сложная
математика не может "улучшить" то, что
индивидуум не хочет менять". То есть,
если требуемая согласованность не получена,
следует возвратиться к опросу, изменяя
формулировки
вопросов,
а
при
необходимости и критерии.

37.

Пример выполнения
контрольной работы
Рассматривается задача выбора наиболее предпочтительного варианта дачного
участка при наличии у ЛПР (лица, принимающего решение) нижеследующих
допустимых альтернатив.
Участок А: недалеко от города, есть автобус и электричка, хорошая автодорога.
Место в низине, близко к болоту. Ежегодно будет проблема с осушением и привозом
доп. земли на грядки, опила. Есть небольшой домик на участке, печь железная,
электрическая, есть во дворе баня, туалет. Все это требует косметического ремонта,
но жить можно. Требуется электрификация. Стоимость очень выгодная. Участок
небольшой.
Участок В: не близко к городу, дорога грунтовая. Вблизи дачного кооператива –
хороший ягодный лес, речка. На участке построен утепленный сарай, есть
фундамент для дома. Проведен водопровод для полива, есть электричество, земля
для посадок идеальна. Стоимость средняя, продавец стремится продать быстрее.*
Участок С: не очень близко к городу, но ближе, чем В, есть электричка, близко
станция. Участок на равнине, почва плодородная. Дом двухэтажный, теплый, с
хорошей печкой, есть электричество и газ, собственная скважина с питьевой водой.
Грядки разбиты, есть сарай, площадь участка велика. Стоимость выше средней.

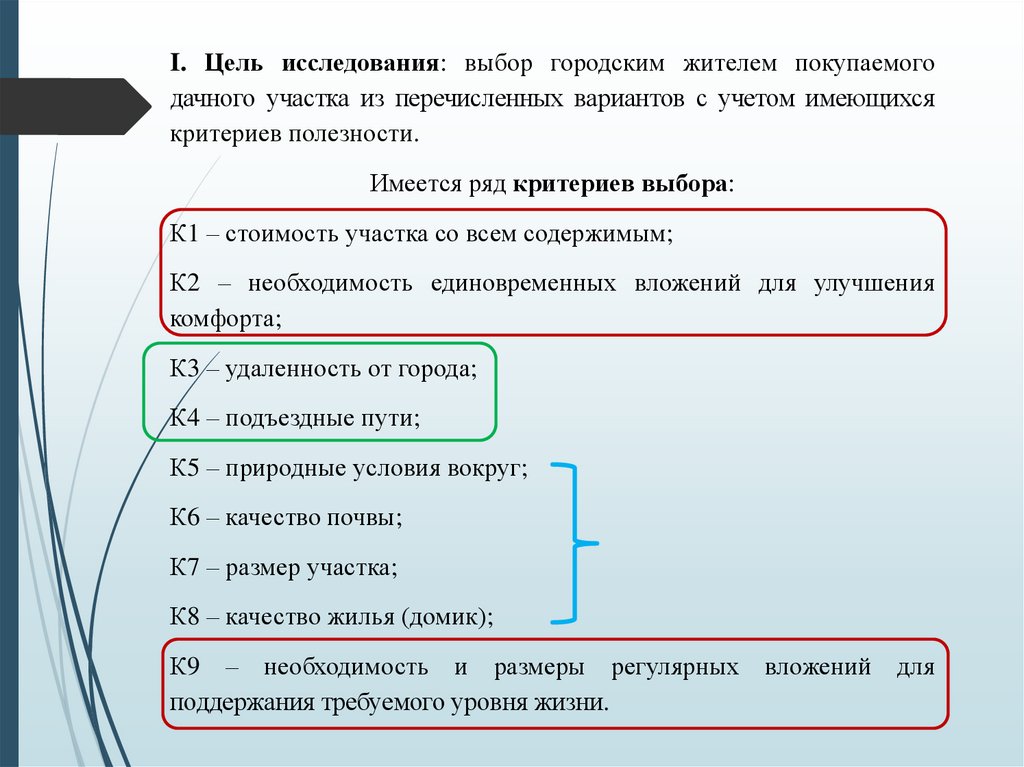
38.

I. Цель исследования: выбор городским жителем покупаемого
дачного участка из перечисленных вариантов с учетом имеющихся
критериев полезности.
Имеется ряд критериев выбора:
К1 – стоимость участка со всем содержимым;
К2 – необходимость единовременных вложений для улучшения
комфорта;
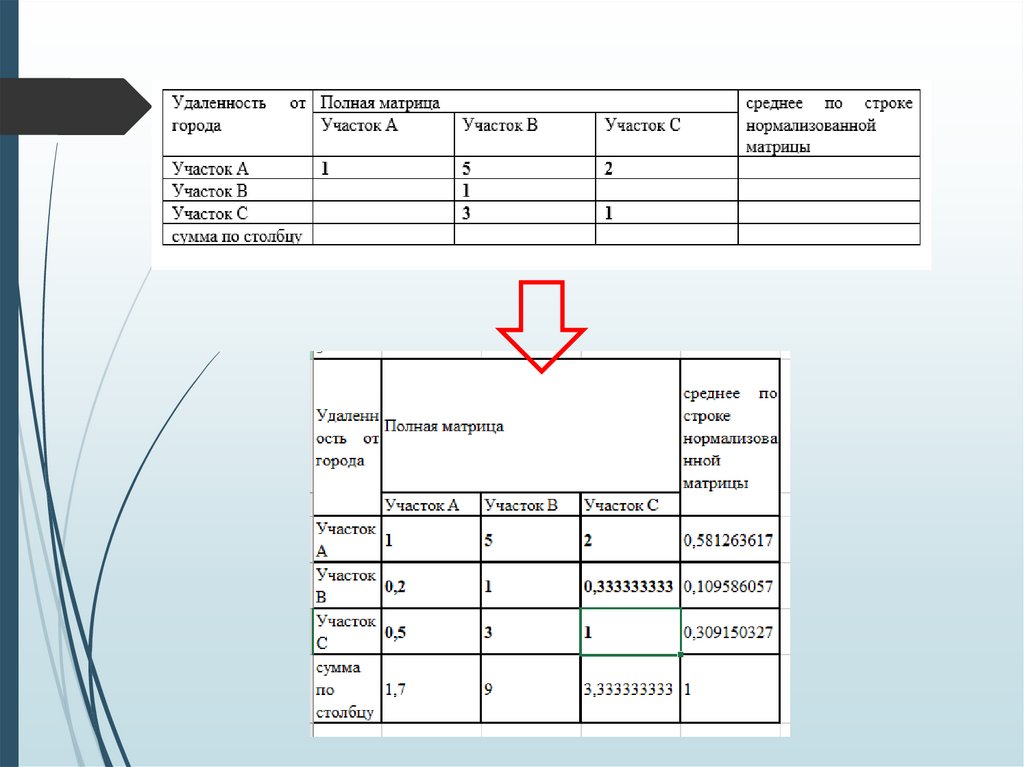
К3 – удаленность от города;
К4 – подъездные пути;
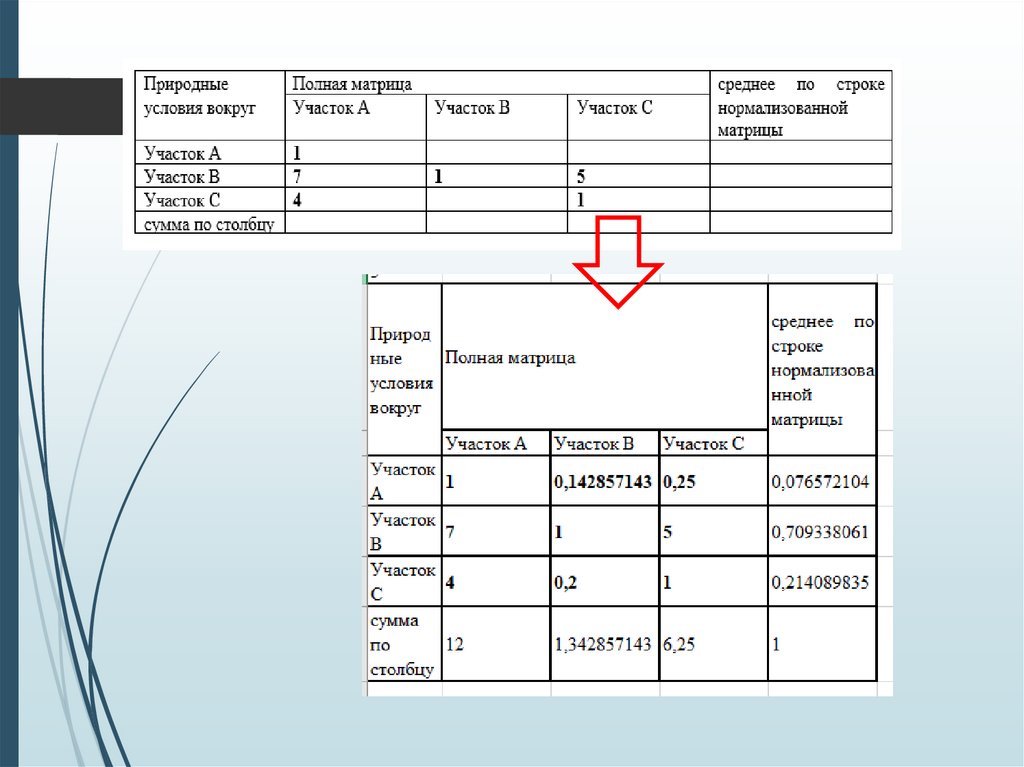
К5 – природные условия вокруг;
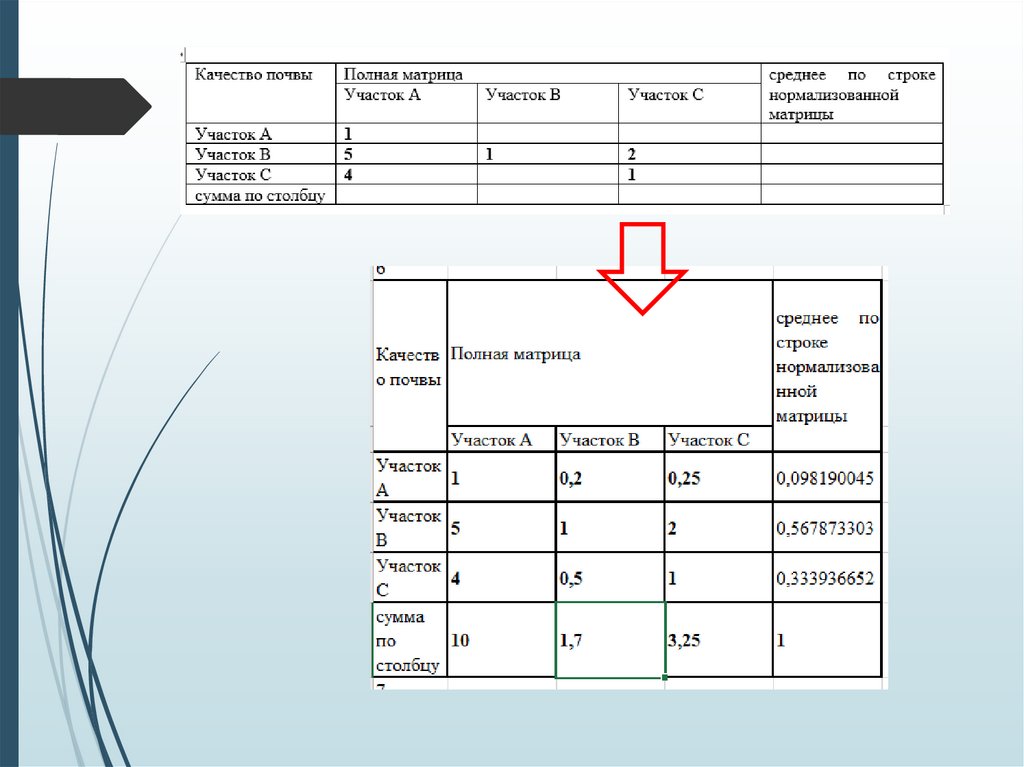
К6 – качество почвы;
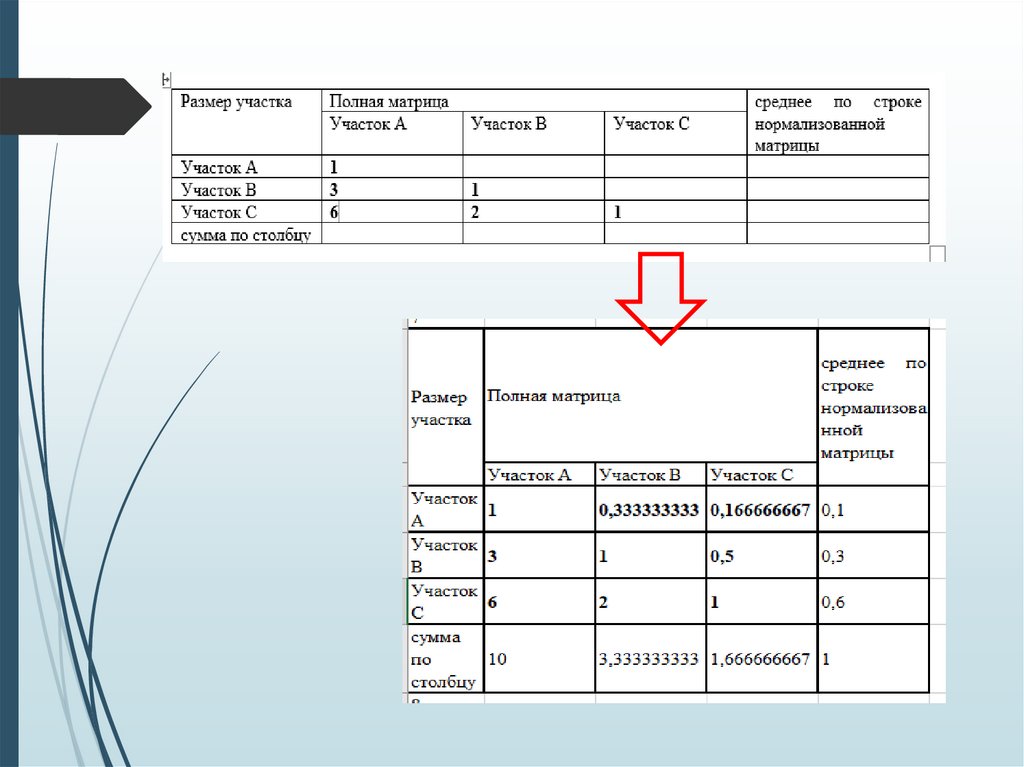
К7 – размер участка;
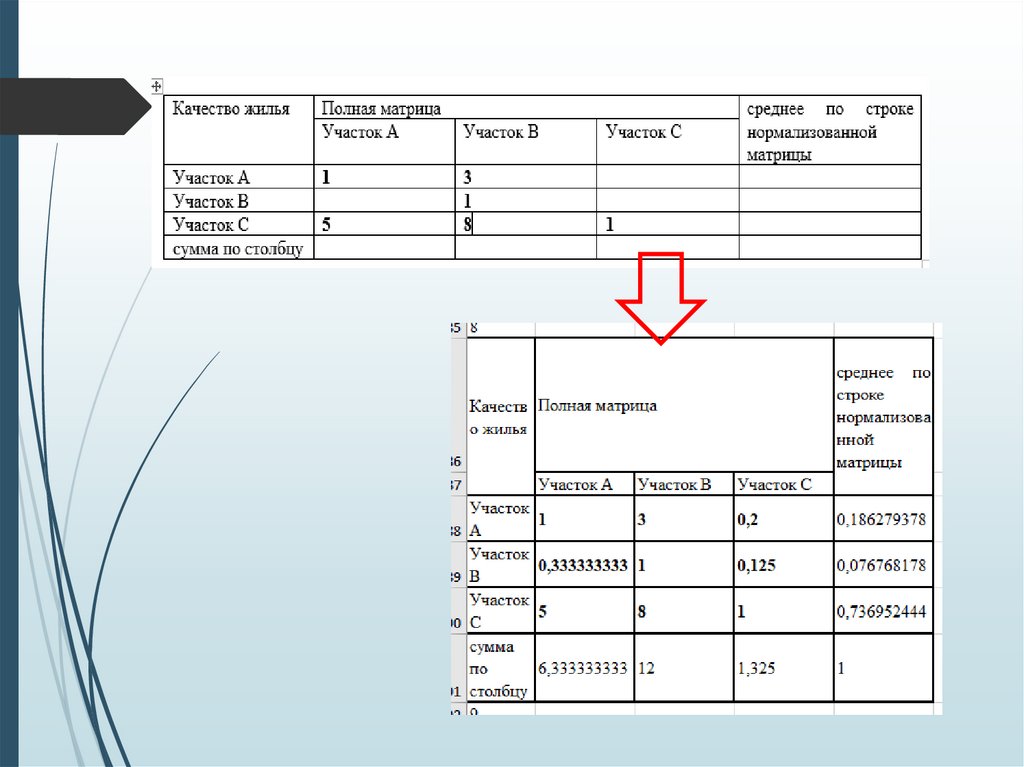
К8 – качество жилья (домик);
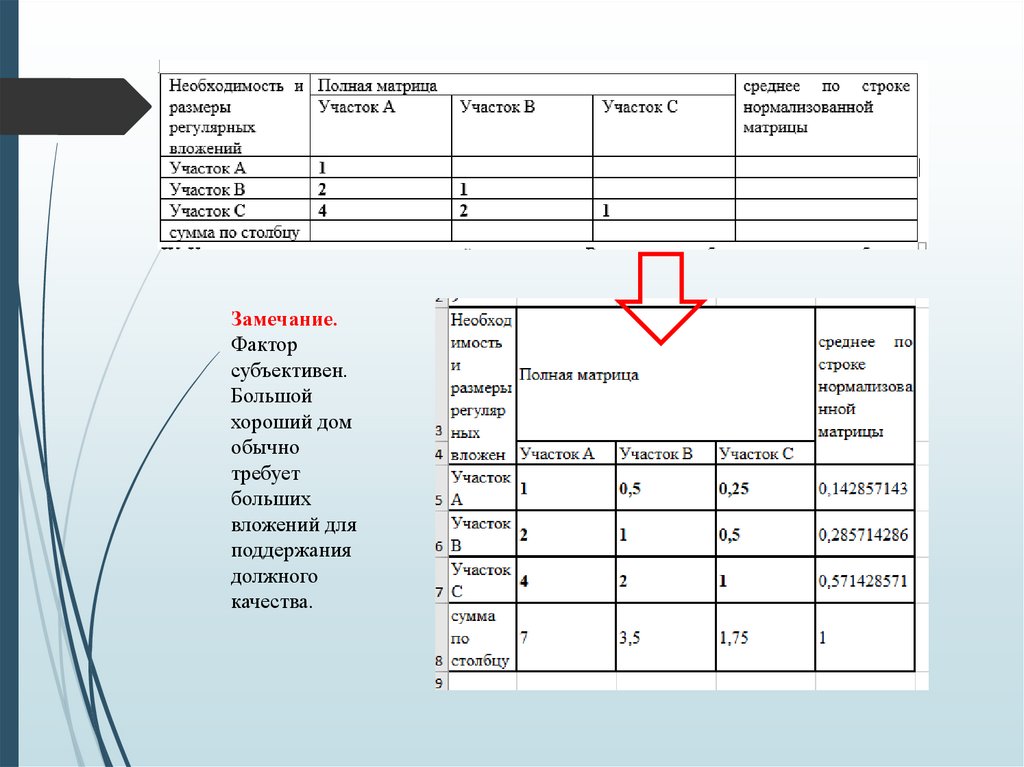
К9 – необходимость и размеры регулярных вложений для
поддержания требуемого уровня жизни.

39.

Критерии объединены в группы, образующие
элементы иерархии более высокого уровня:
«финансы» Р1={К1, К2, К9},
«как добираться» P2 ={К3, К4},
«пользовательские качества» Р3 ={K5, К6, К7, К8}.
Далее определяем относительную важность критериев
с учетом важности групп Р1, Р2, Р3 согласно таблице
их взаимной относительной важности. Финансовые
факторы существенно превосходят по важности
особенности «доставки» владельца до участка, и
незначительно – качества участка.

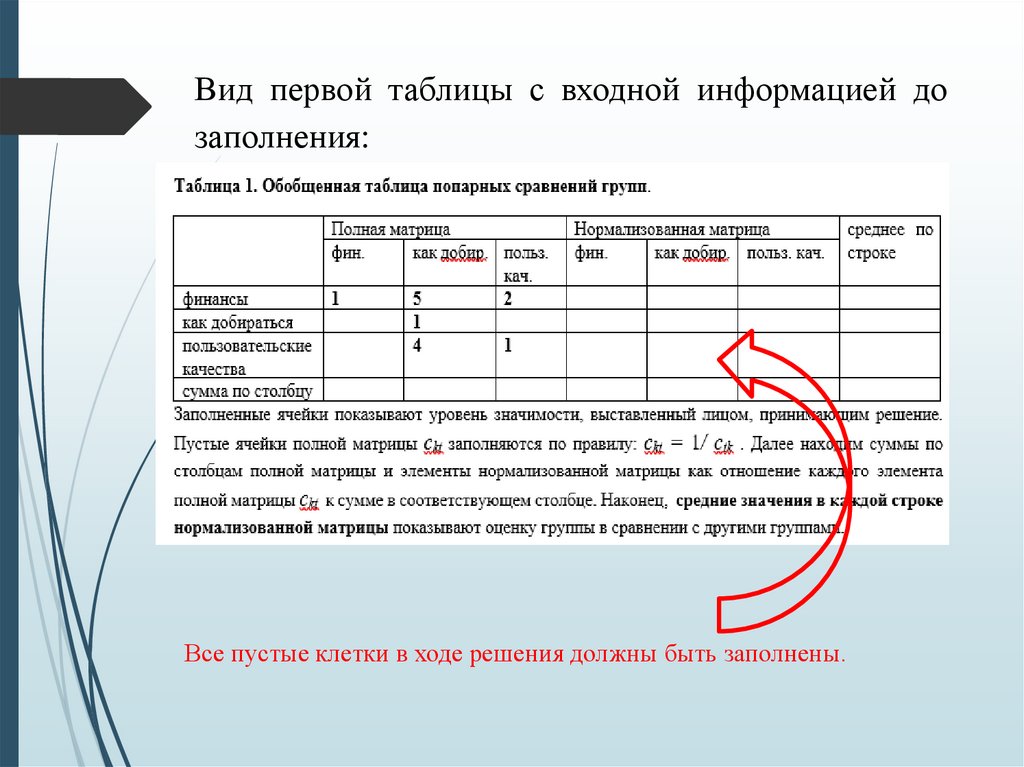
40.

Вид первой таблицы с входной информацией до
заполнения:
Все пустые клетки в ходе решения должны быть заполнены.

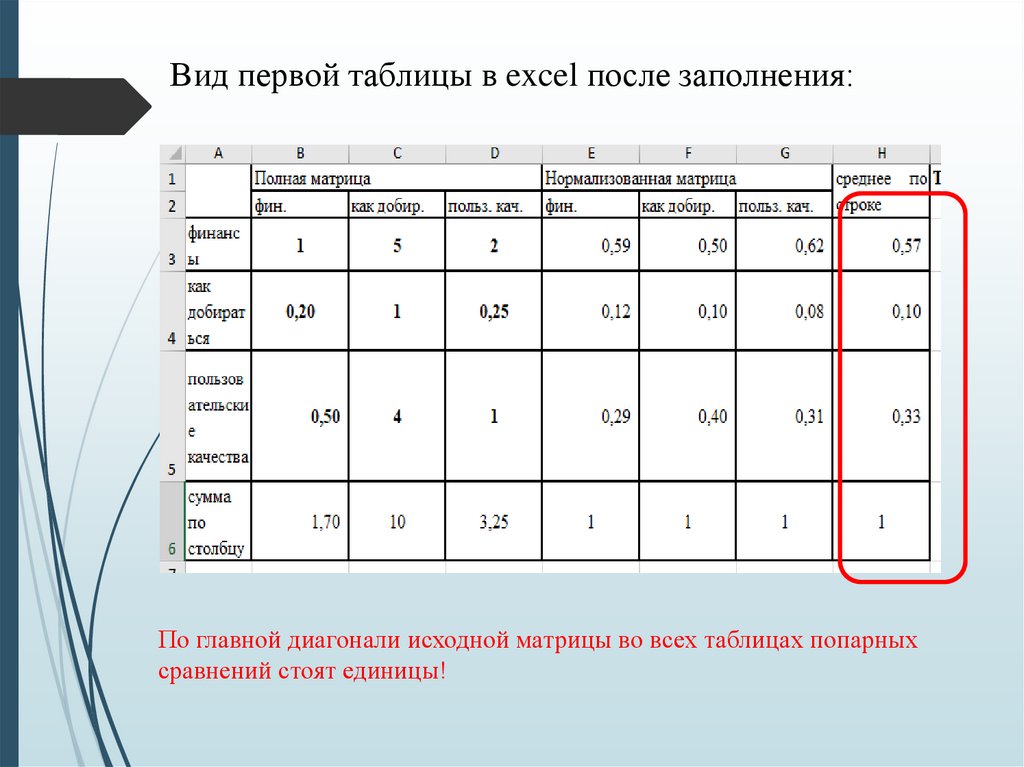
41.

Вид первой таблицы в excel после заполнения:
По главной диагонали исходной матрицы во всех таблицах попарных
сравнений стоят единицы!

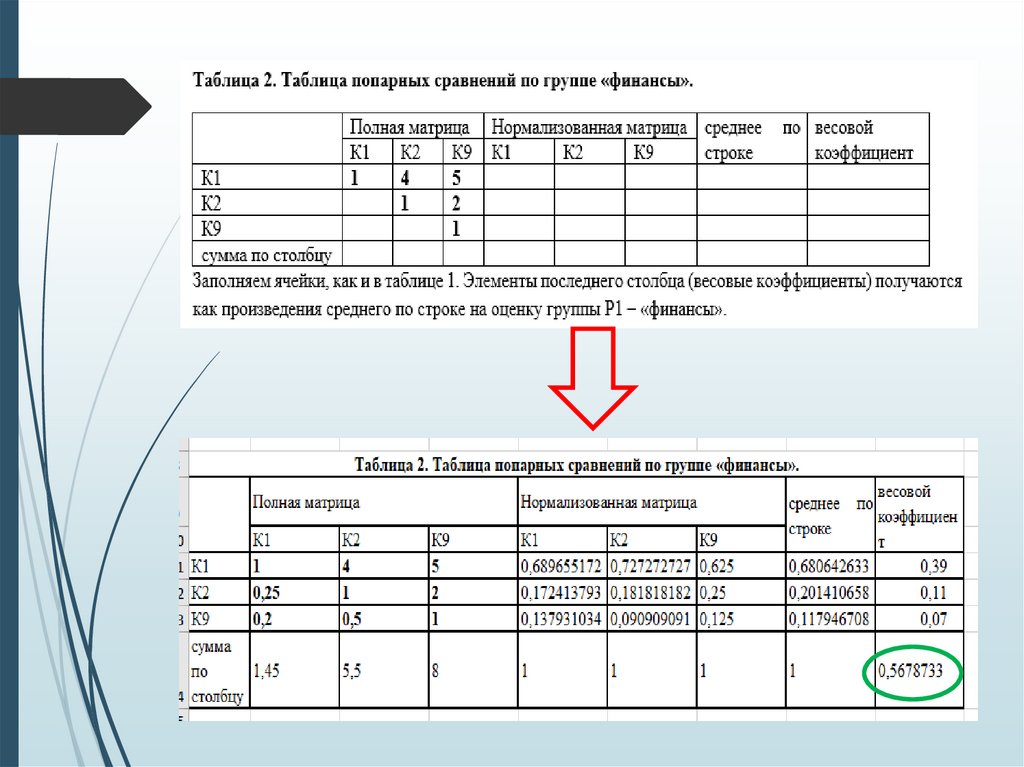
42.

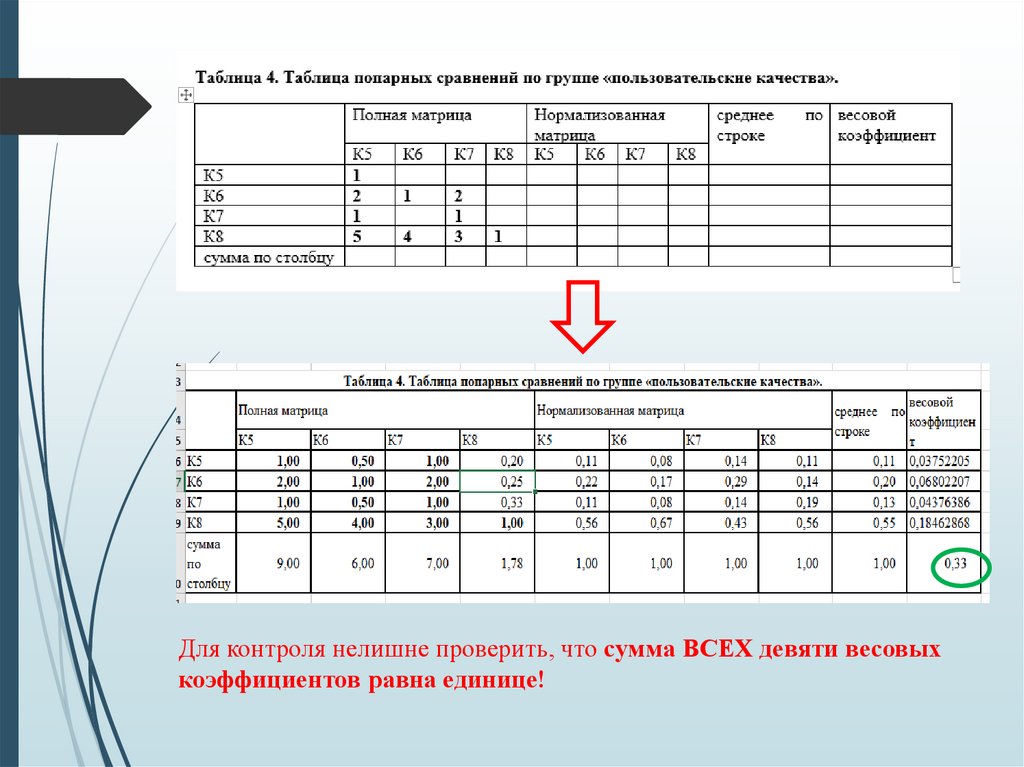
43.

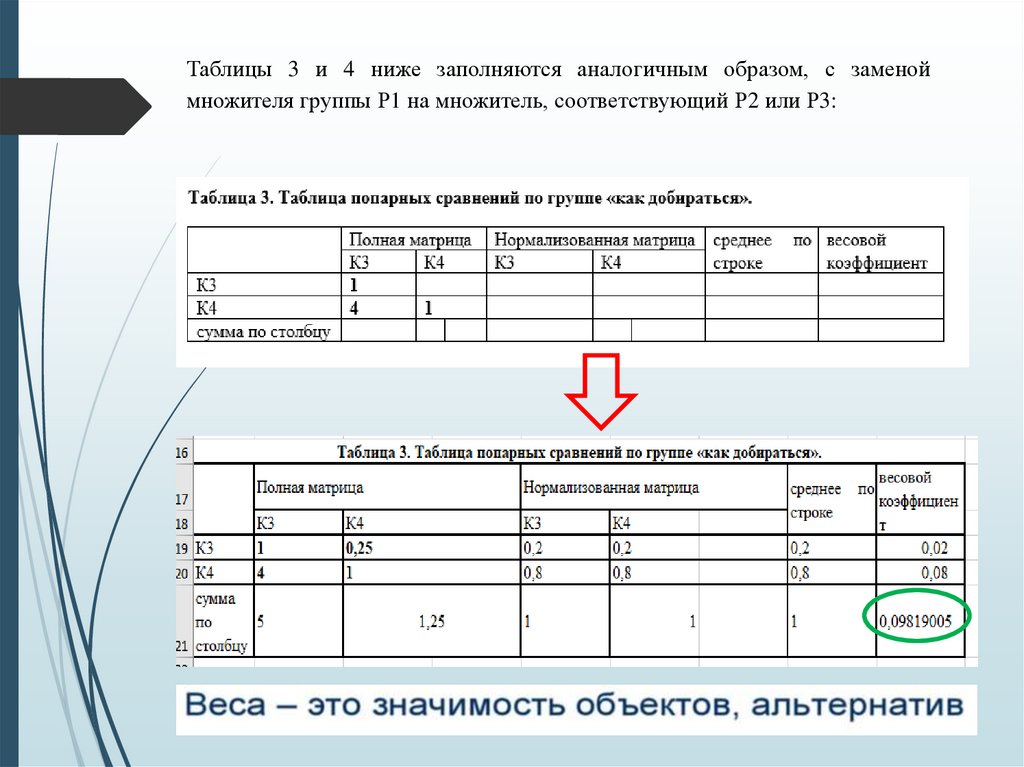
Таблицы 3 и 4 ниже заполняются аналогичным образом, с заменой
множителя группы Р1 на множитель, соответствующий Р2 или Р3:

44.

Для контроля нелишне проверить, что сумма ВСЕХ девяти весовых
коэффициентов равна единице!

45.

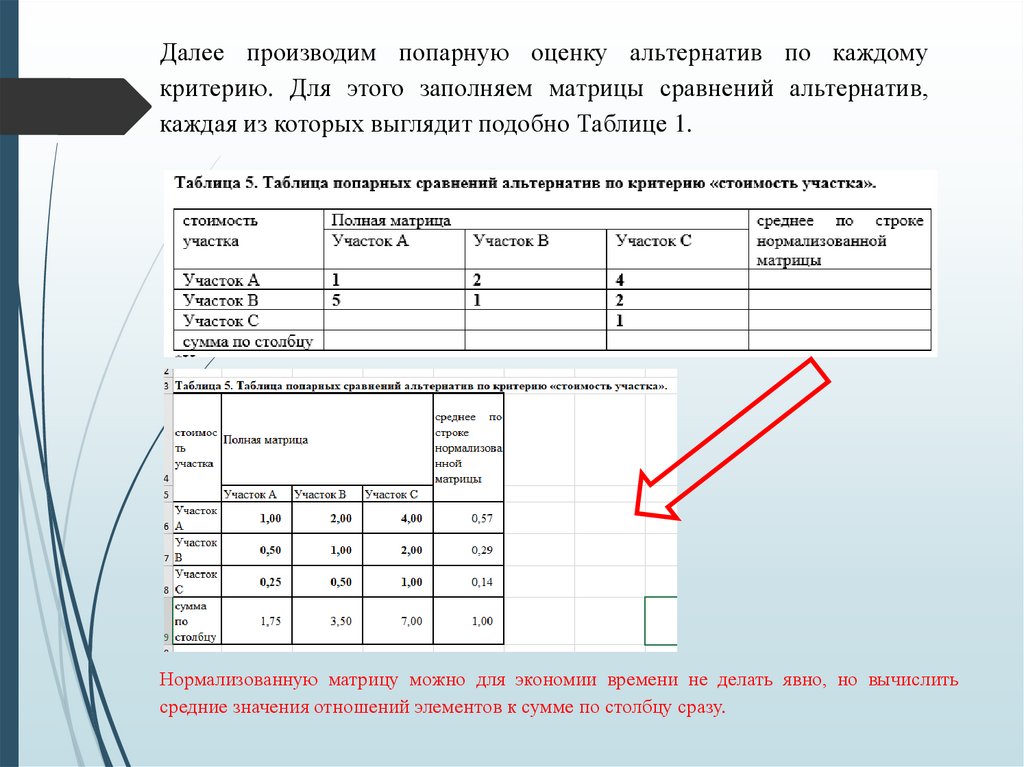
Далее производим попарную оценку альтернатив по каждому
критерию. Для этого заполняем матрицы сравнений альтернатив,
каждая из которых выглядит подобно Таблице 1.
Нормализованную матрицу можно для экономии времени не делать явно, но вычислить
средние значения отношений элементов к сумме по столбцу сразу.

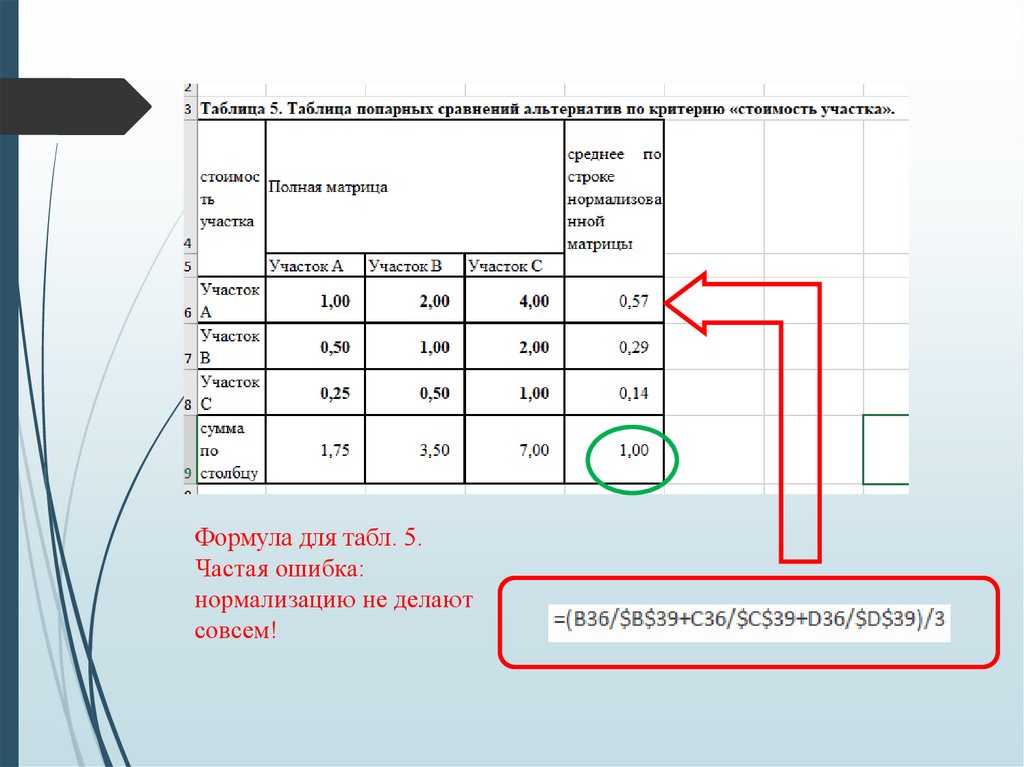
46.

Формула для табл. 5.
Частая ошибка:
нормализацию не делают
совсем!

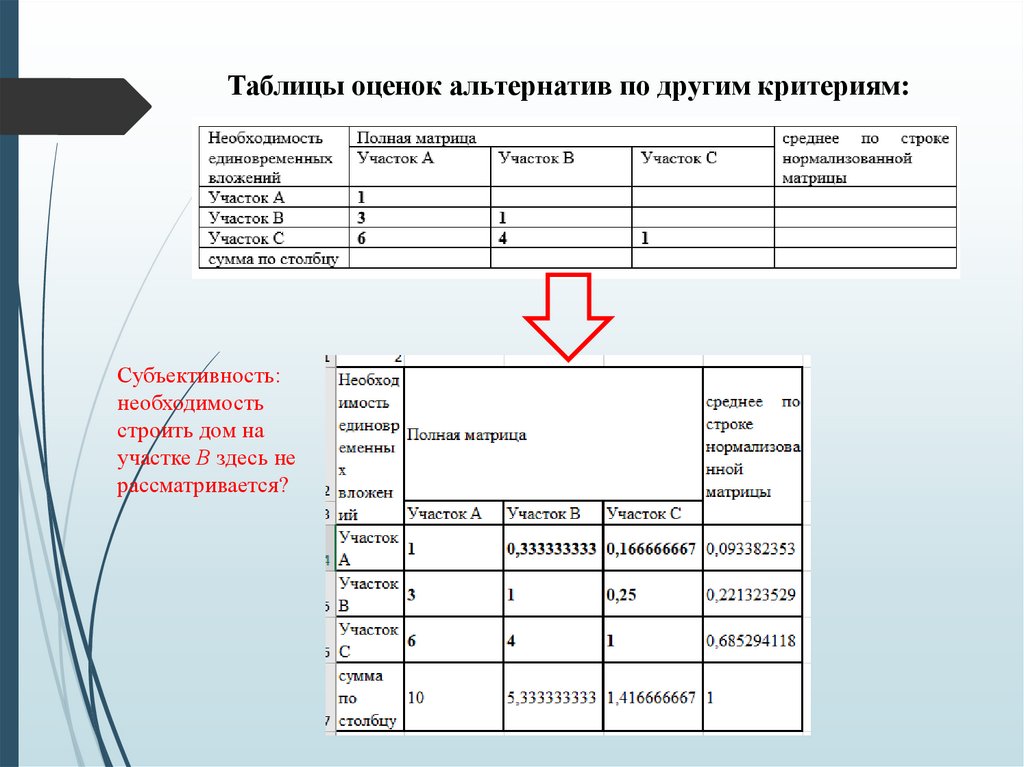
47.

Таблицы оценок альтернатив по другим критериям:
Субъективность:
необходимость
строить дом на
участке В здесь не
рассматривается?

48.

49.

50.

51.

52.

53.

54.

Замечание.
Фактор
субъективен.
Большой
хороший дом
обычно
требует
больших
вложений для
поддержания
должного
качества.

55.

Находим комплексную оценку каждой альтернативы:
В контрольной работе требуется, сделав расчеты, ответить на вопрос о
выборе. Иногда возможны дополнительные вопросы по влиянию
критериев на результат выбора, значимости критериев на взгляд ЛПР и
др.

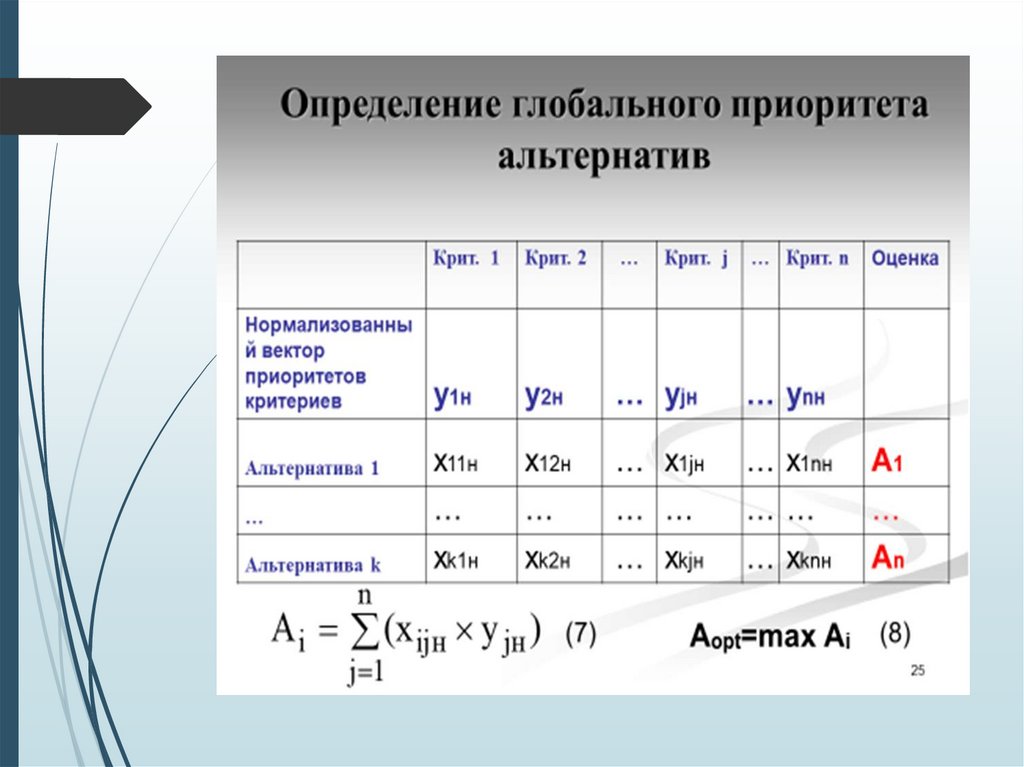
56.

Итоговый вектор приоритетов – рейтинг
альтернатив. Каждой альтернативе (каждому
возможному решению) ставится в соответствие
положительное число – приоритет. Приоритет
количественно
выражает
важность
(предпочтительность, вероятность, оптимальность и
т.п.) альтернативы в соответствии с главным
критерием. Сумма приоритетов всех альтернатив
равна единице. Вследствие этого часто допустимо
отождествление приоритетов с вероятностями. Для
поддержки принятия решения в основном с
помощью
итогового
вектора
приоритетов
производится
интерпретация
результатов
применения метода. Например, принимается
решение с наибольшим приоритетом, отвергается
решение с наименьшим приоритетом и т.п.

57.

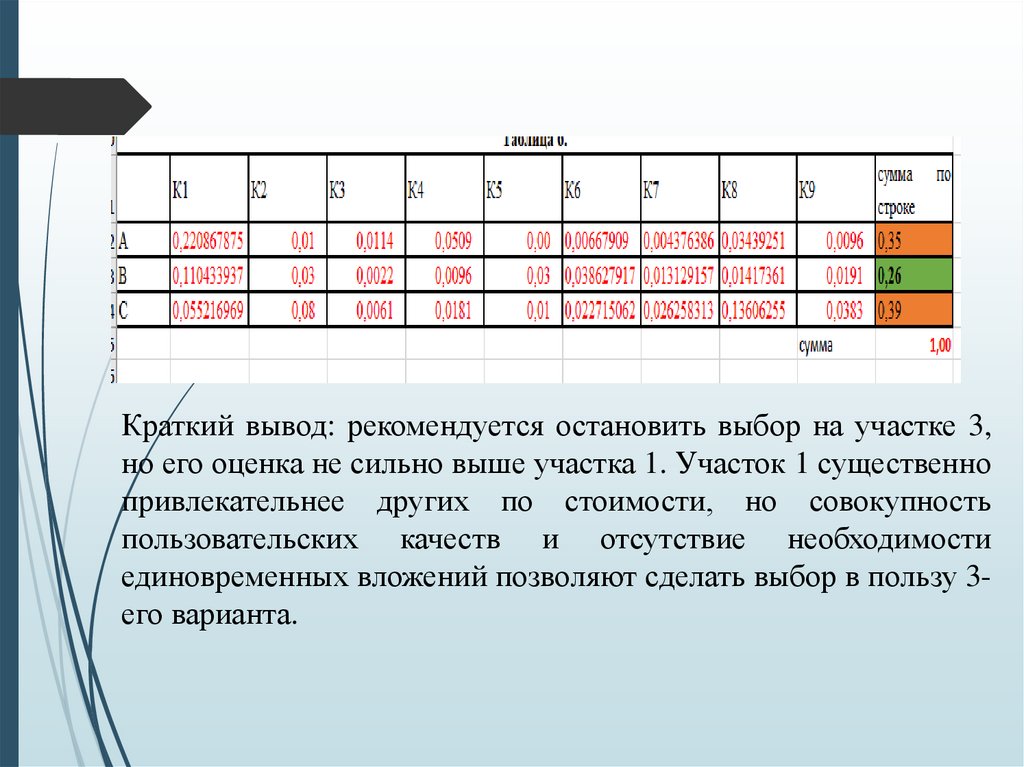
Краткий вывод: рекомендуется остановить выбор на участке 3,
но его оценка не сильно выше участка 1. Участок 1 существенно
привлекательнее других по стоимости, но совокупность
пользовательских качеств и отсутствие необходимости
единовременных вложений позволяют сделать выбор в пользу 3его варианта.

58.

Устойчивость вектора приоритетов – качественная
характеристика
чувствительности
значений
приоритетов к малым изменениям данных или
структуры
модели.
Очевидно,
данные,
использующиеся для принятия решений, всегда более
или менее неточны. Поэтому чем меньше
чувствительность значений приоритетов, тем
больше обоснованность использования этих
приоритетов для поддержки принятия решения. В
зависимости от решаемой задачи определяется
понятие «существенное изменение рейтинга» (смена
лидера, смена аутсайдера и т.п.). Если при малых
изменениях данных или структуры рейтинг
изменяется несущественно, то он считается
устойчивым.

59.

Возможные дополнительные вопросы:
-
-
Имеются ли среди критериев зависимые? Независимые?
Если ЛПР желает, чтобы выбор был в пользу иной
альтернативы,
как
нужно
изменить
входную
информацию (это способ манипуляции результатами)?
Какой из критериев, на взгляд студента, можно добавить,
а какой лучше убрать?
Оценки по каким критериям (1-2) определили итоговый
выбор?
Почему на главной диагонали матриц всегда стоят
единицы? Что означают единицы в других ячейках?
Какова роль «весов» групп? «Весов» критериев?
Когда целесообразно применять МАИ?
Как изменится структура входной и обрабатываемой
информации, если критерии НЕ группировать?
Зачем группировать критерии?

60.

Ссылки:
https://www.hse.ru/mirror/pubs/share/204810376
https://studme.org/98142/informatika/metod_analiz
a_ierarhiy_saati
https://www.innov.ru/science/economy/vyborpredpochtitelnogo-varianta-po/ - рассмотрен
подробный пример
http://vamocenka.ru/metod-analiza-ierarxijprocedura-primeneniya/