Похожие презентации:
Метод анализа иерархий (МАИ)
1. МАИ
Метод анализа иерархий2. Метод анализа иерархий
Цель метода анализа иерархий обоснованиевыбора наилучшей из предлагаемых альтернатив,
характеристики которых являются векторами с
разнородными, в том числе и с нечетко
определенными, отдельными компонентами.
Суть метода анализа иерархий заключается в
поэтапном решении следующих взаимосвязанных
частных задач:
построение иерархической структуры показателей
(признаков);
оценивание значимости отдельных частных показателей для
каждого уровня иерархии;
сравнение имеющихся альтернатив и выбор наилучшей из
них.
3. Метод анализа иерархий
Метод анализа иерархии включает процедурысинтеза множественных суждений, базирующихся на
результатах парных сравнений, которые затем выражаются
численно,
оценки приоритетности (важности) критериев (отдельных
показателей), а также
оценки альтернативных решений и
нахождения наилучшего из них.
Полученные результирующие значения являются
оценками в шкале отношений, что соответствует
жестким оценкам.
4. Метод анализа иерархий
Исходным материалом, на основании которого ЛПРможет получить достаточное, четкое и ясное
представление о превосходстве одного элемента
над другим, являются интуиция и субъективные
оценки, несмотря на то, что суждения и их
интенсивность характеризуют выражение внутренних
чувств и склонностей конкретных экспертов.
Суждения расширяют рамки общения, укрупняя
элементы, имеющиеся на определенном уровне
иерархии.
5. Основные этапы метода анализа иерархий
1 этап. Описание проблемы и определение целиисследований.
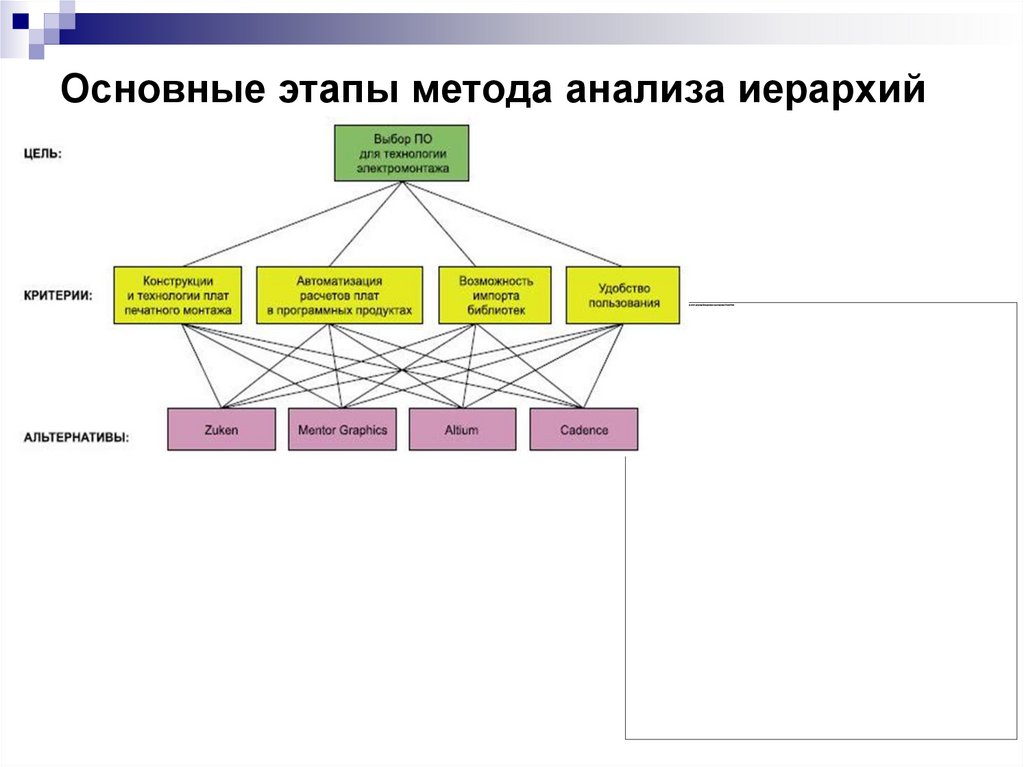
2 этап. Построение иерархии,
начиная с вершины (цели с точки зрения
управления),
через промежуточные уровни (критерии, от которых
зависят последующие уровни),
к самому нижнему уровню (который обычно является
перечнем альтернатив).
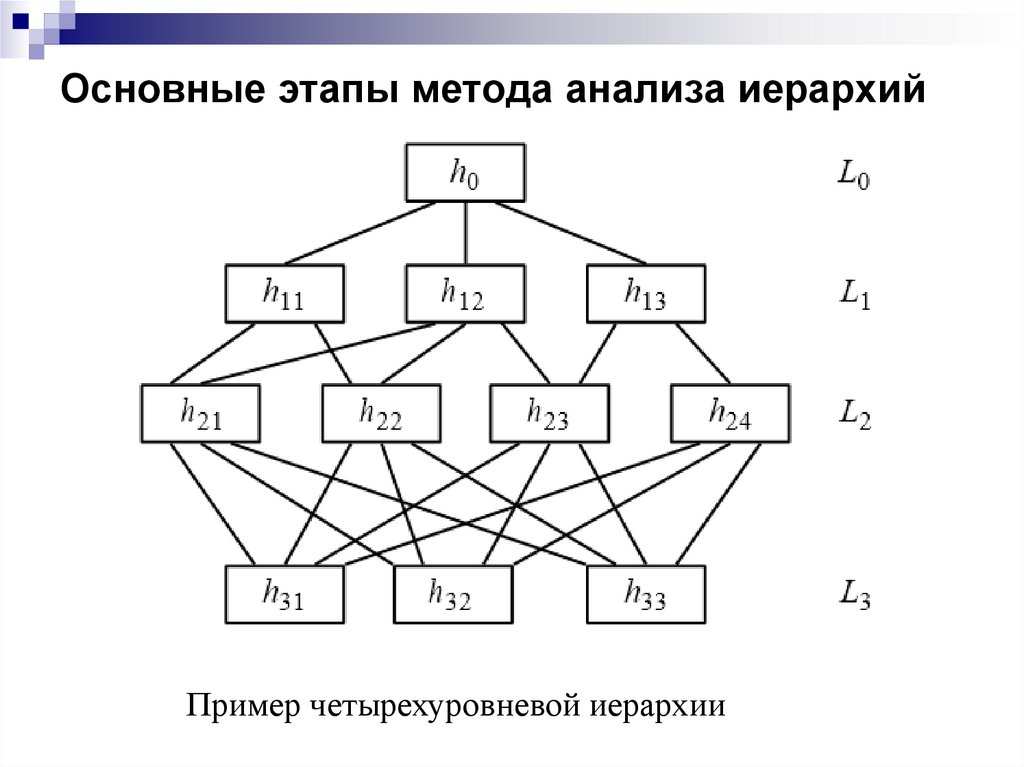
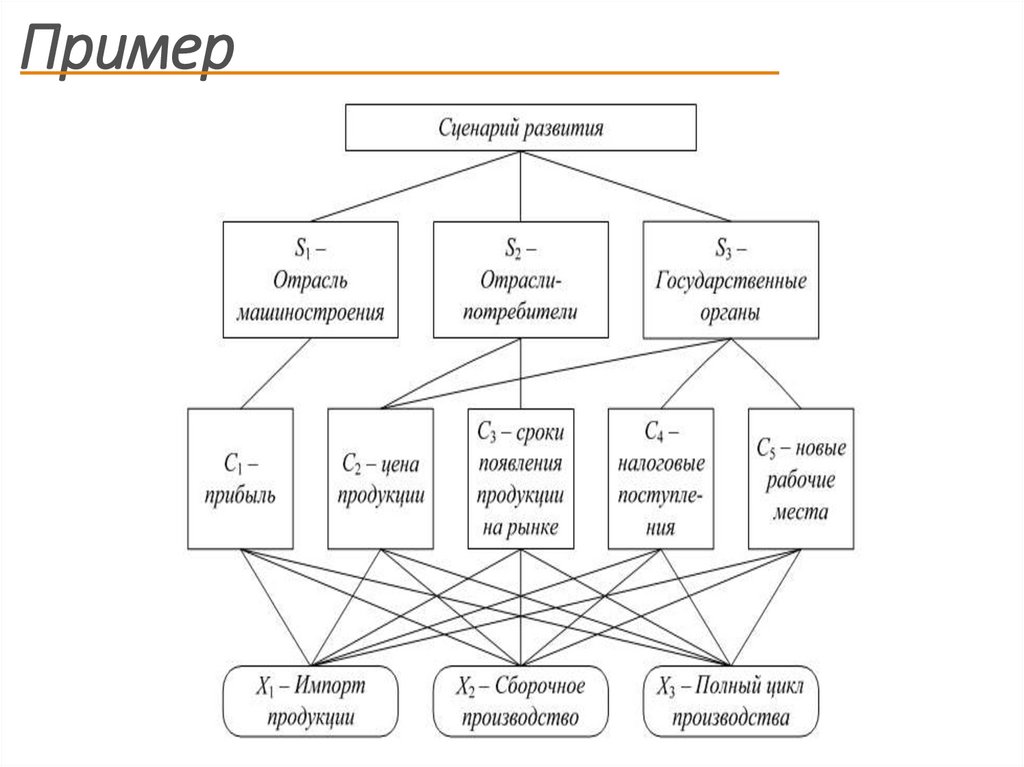
6. Основные этапы метода анализа иерархий
Пример четырехуровневой иерархии7. Основные этапы метода анализа иерархий
8. Основные этапы метода анализа иерархий
3 этап. Построение матриц влияния элементовверхнего (предыдущего) уровня на элементы нижнего
(следующего) уровня (для каждого из нижних уровней)
по одной матрице для каждого элемента,
примыкающего сверху уровня.
В полной простой иерархии любой элемент
воздействует на каждый элемент примыкающего
сверху уровня.
Элементы каждого уровня сравниваются друг с
другом относительно степени их воздействия на
элемент предыдущего уровня и получают
квадратную матрицу суждений.
9. Основные этапы метода анализа иерархий
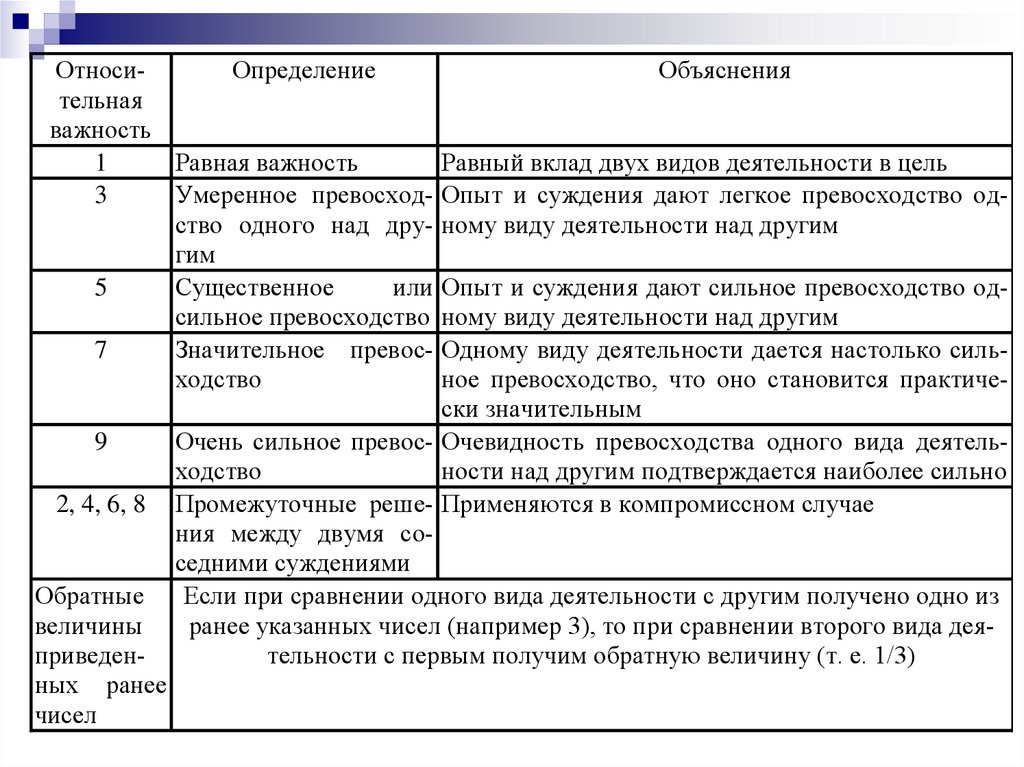
3 этап (продолжение). Парные сравнения проводятся втерминах определения степеней доминирования
(предпочтения) одного из элементов над другим в
соответствии со шкалой Саати.
Для получения каждой матрицы требуется n(n -1)/2 суждений
(парных сравнений).
Результатом этапа 3 (сравнения значимости влияния элементов
следующего уровня на элементы предыдущего уровня) является
набор квадратных матриц N1, N2, , Nk с элементами (aij, i, j = 1,
2,…, n), где k число элементов предыдущего уровня иерархии,
n число элементов следующего уровня иерархии.
Если иерархическая структура не является полной простой
иерархией, то возможно уменьшение количества сравнений, т. е.
упрощение процесса получения результатов парных сравнений.
10.
ОтносиОпределениетельная
важность
1
Равная важность
3
Умеренное превосходство одного над другим
5
Существенное
или
сильное превосходство
7
Значительное превосходство
9
2, 4, 6, 8
Обратные
величины
приведенных ранее
чисел
Объяснения
Равный вклад двух видов деятельности в цель
Опыт и суждения дают легкое превосходство одному виду деятельности над другим
Опыт и суждения дают сильное превосходство одному виду деятельности над другим
Одному виду деятельности дается настолько сильное превосходство, что оно становится практически значительным
Очень сильное превос- Очевидность превосходства одного вида деятельходство
ности над другим подтверждается наиболее сильно
Промежуточные реше- Применяются в компромиссном случае
ния между двумя соседними суждениями
Если при сравнении одного вида деятельности с другим получено одно из
ранее указанных чисел (например 3), то при сравнении второго вида деятельности с первым получим обратную величину (т. е. 1/3)
11. Основные этапы метода анализа иерархий
3 этап (продолжение).a11
a21
a12
a22
a13
a23
… a1n
… a2n
…
…
…
…
an1
an2
an3
… ann
Квадратную матрицу An n в которой все элементы
a ji a1 ; i, j 1, n ,
ij
называют обратносимметрической.
В положительной обратносимметрической квадратной матрице
max n .
12. Основные этапы метода анализа иерархий
4 этап Определение весов элементов одного уровняИсходная информация. Иерархия построена, проведены
субъективные парные сравнения и составлен набор
квадратных матриц N1, N2, …, Nk с элементами (aij, i, j = 1,
2, …, n); где k число элементов предыдущего уровня
иерархии, а n число элементов следующего уровня
иерархии.
Задача. Из группы матриц парных сравнений
сформировать набор локальных приоритетов, которые
выражают относительное влияние множества
элементов данного уровня на элементы примыкающего
сверху уровня.
13. Основные этапы метода анализа иерархий
4 этап (продолжение) Определение весов элементоводного уровня
Способ решения. Относительную значимость
(величину, ценность, желательность или
вероятность) каждого отдельного элемента
определяем на основе вычисления собственных
векторов, соответствующих максимальным
собственным числам, для всех матриц, а затем
нормирования результата для получения вектора
приоритетов.
14. Основные этапы метода анализа иерархий
4 этап (продолжение) Определение весов элементоводного уровня
Технология. Квадратная матрица имеет собственные
векторы и собственные значения.
Собственный вектор, соответствующий наибольшему
собственному значению достаточно адекватно
отражает сравнительную значимость (важность)
факторов или результатов в проблемной ситуации.
На факторах с наибольшей важностью
концентрируется внимание при решении задачи или
разработке плана действия.
15. Основные этапы метода анализа иерархий
4 этап (продолжение) Определение весов элементоводного уровня
Вычисление собственных векторов требует трудоемких
вычислений. В методе анализа иерархий используется
упрощенный подход (для вычисления собственного
вектора), позволяющий получить хорошие
приближения к приоритетам, основанный на
вычислении среднего геометрического.
Нормирование компонент осуществляется путем
деления каждой компоненты вектора на сумму всех
компонент этого вектора
wj
n
wj
n a jl w j
a
l 1
l
l
16. Основные этапы метода анализа иерархий
4 этап (продолжение) Определение весов элементоводного уровня
Если ввести в рассмотрение матрицу влияний
элементов нижнего уровня на элементы предыдущего
уровня Wl, где l номер уровня иерархии, то векторы wj
будут являться ее столбцами.
17. Основные этапы метода анализа иерархий
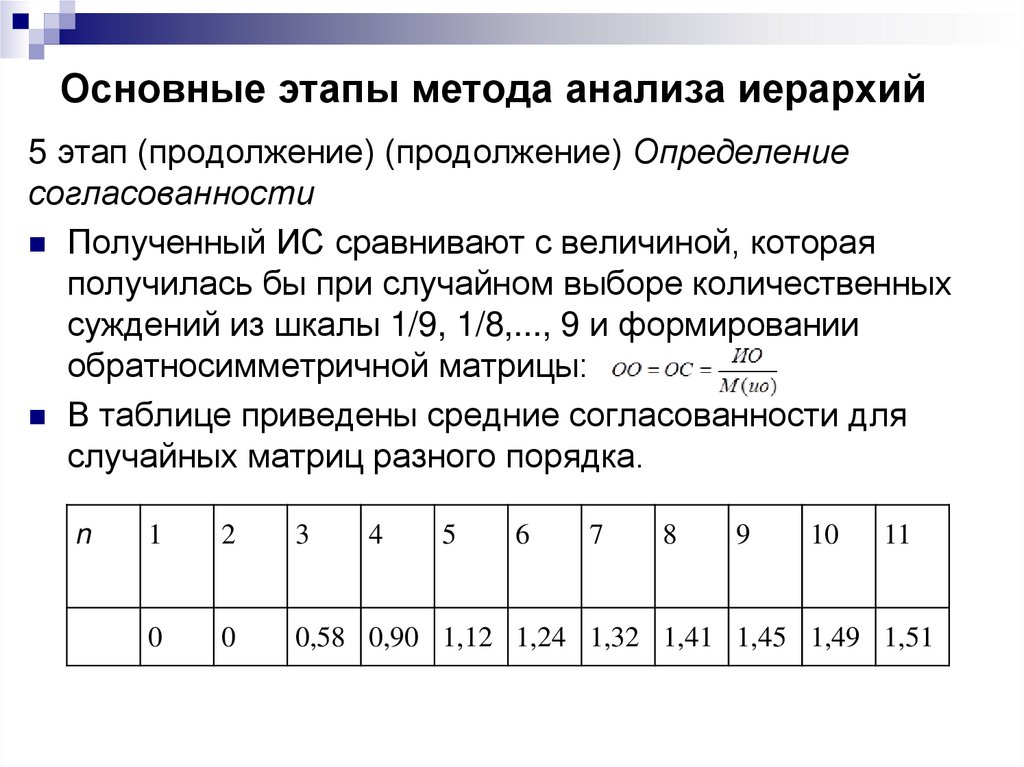
5 этап Определение согласованностиВместе (одновременно) с получением матриц парных
сравнений необходимо провести оценки степени
отклонения от согласованности. В противном случае,
для различных матриц, для которых такие отклонения
превышают установленные пределы, эксперту следует
перепроверить суждения, отраженные в матрице.
Полученная матрица в общем случае несогласованна.
Анализ согласованности целесообразно проводить для каждой
матрицы непосредственно после ее формирования, так как в
противном случае оценки весовых коэффициентов элементов
конкретного уровня могут быть вычислены неправильно по
несогласованным мнениям экспертов, что может повлечь
необходимость пересчета нескольких матриц, т. е. влечет
возрастание объема бесполезных вычислений.
18. Основные этапы метода анализа иерархий
5 этап (продолжение) Определение согласованностиСтепень согласованности для каждой матрицы
приближенно вычисляется следующим способом:
суммируется каждый столбец матрицы суждений, и
сумма первого столбца умножается на величину
первой компоненты нормализованного вектора
приоритетов, сумма второго столбца на вторую
компоненту и т. д.
Полученные числа суммируются и получается
величина

















































 Математика
Математика








