Похожие презентации:
Метод найменших квадратів. (Тема 4)
1. Метод найменших квадратів
Тема 4Метод найменших
квадратів
Лектор: к.е.н., доц., доцент кафедри вищої математики,
економетрії і статистики ДЕМЧИШИН М.Я.
1
2. План
4.1. Суть методу найменших квадратів (МНК).4.2. Передумови застосування МНК.
4.3. Система нормальних рівнянь.
2
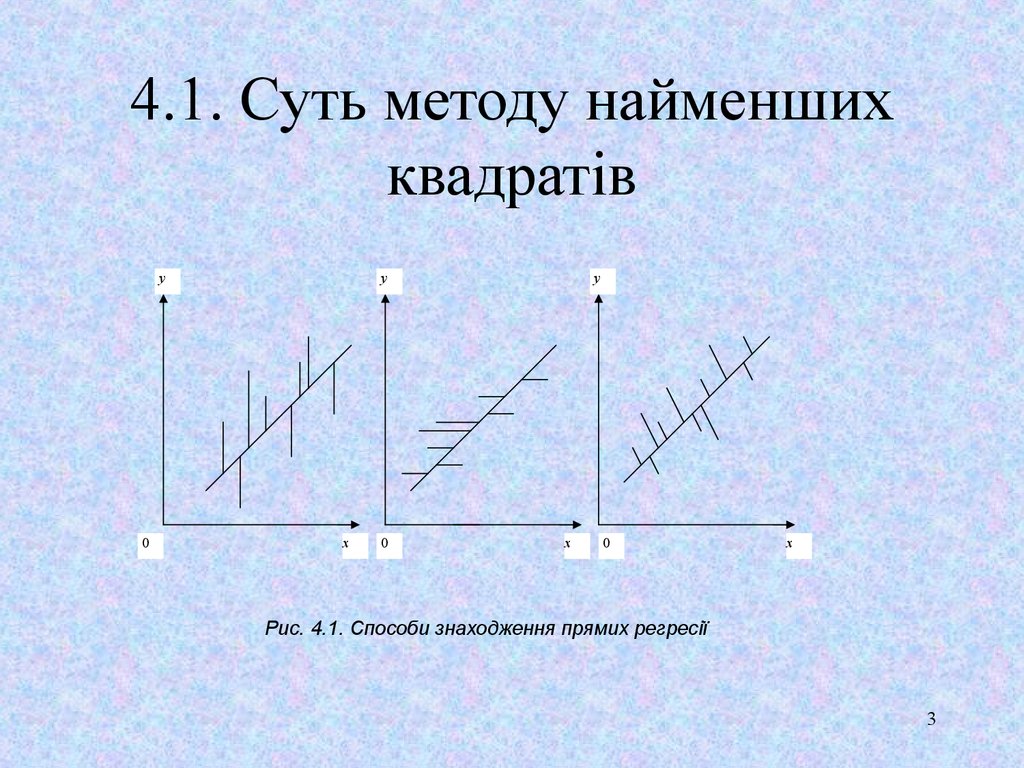
3. 4.1. Суть методу найменших квадратів
y0
y
x
0
y
x
0
x
Рис. 4.1. Способи знаходження прямих регресії
3
4.
y0
x
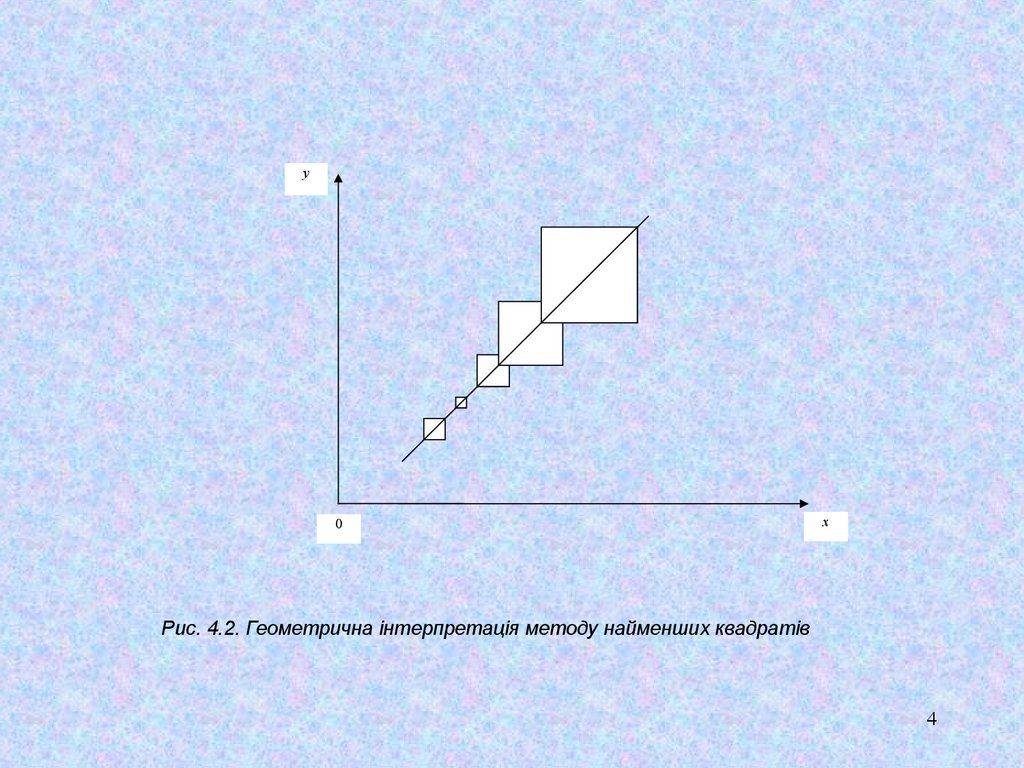
Рис. 4.2. Геометрична інтерпретація методу найменших квадратів
4
5. Суть методу найменших квадратів (МНК)
полягає у знаходженні такої теоретичної лініїрегресії, яка в порівнянні з іншими проходить
найближче до емпіричної лінії регресії,
тобто дає
найменшу суму квадратів відхилень
фактичних значень результативної ознаки від
розрахункових (теоретичних) значень
5
6.
n2
~
y
y
min
i i
i 1
• де y – емпіричні (вихідні) дані показника
• ỹ– теоретичні (розраховані за рівнянням
регресії)
6
7. 4.2. Передумови застосування МНК
1) Існує лінійний зв’язок міжрезультуючою змінною у та факторною
змінною x, який описується рівняннями
регресії
y 0 1x
~
y b0 b1 x
7
8.
i j,
2) Факторна змінна x є детерміністичною (невипадковою) величиною.
3) Математичне сподівання (середнє значення) випадкового вектора дорівнює
нулю, а дисперсія є невеликою постійною додатньою величиною, яка не
залежить від індексу i, тобто
.
E 0
2
2 величинами, тобто для
4) Компоненти вектора є некорельованими
випадковими
D
E
i
i
кожного i
.
i, j 1,2,..., n
5) Часто вважають, що випадкова величина має нормальний закон розподілу з
рівним нулю математичним
і постійною додатньою невеликою
cov i , j сподіванням
0
дисперсією
У даному випадку модель називається класичною нормальною лінійною регресійною
моделлю.
2
•Зауваження. У випадку класичної нормальної лінійної регресійної моделі умова 4
еквівалентна умові статистичної незалежності помилок .
~ N 0,
9. 4.3. Система нормальних рівнянь
Будемо вважати, що зв’язок між ознаками х тау є лінійним і описується лінійним рівнянням
регресії
y b0 b1 x
(4.3)
де у – результуюча змінна; b0, b1– параметри
рівняння регресії; х – факторна змінна; ε–
випадкова величина.
9
10.
У загальному випадку nарна лінійна регресія єлінійною функцією мiж залежною змінною У i
однiєю пояснюючою змінною Х:
y b0 b1 x
Це спiввiдношення називається теоретичною
лінійною регресiйною моделлю
b0 i b1 - теоретичні параметри
(теоретичні коефіцієнти) peгpeciї.
10
11.
x1x2
x3
. . . xn-1
xn
y1
y2
y3
...
yn-1
yn
11
12.
nn
n
i 1
i 1
i 1
ui ( yi yi ) ( yi b0 b1xi )
n
n
u y
i 1
n
ui
i 1
2
i
i 1
n
n
i
yˆ i yi aˆ0 aˆ1 xi
метод найменших
модулів (МНМ).
i 1
n
( yi yˆi ) ( yi b0 b1 xi )
i 1
2
i 1
2
~
Q y y min
2
метод найменших
квадратів (МНК).
12
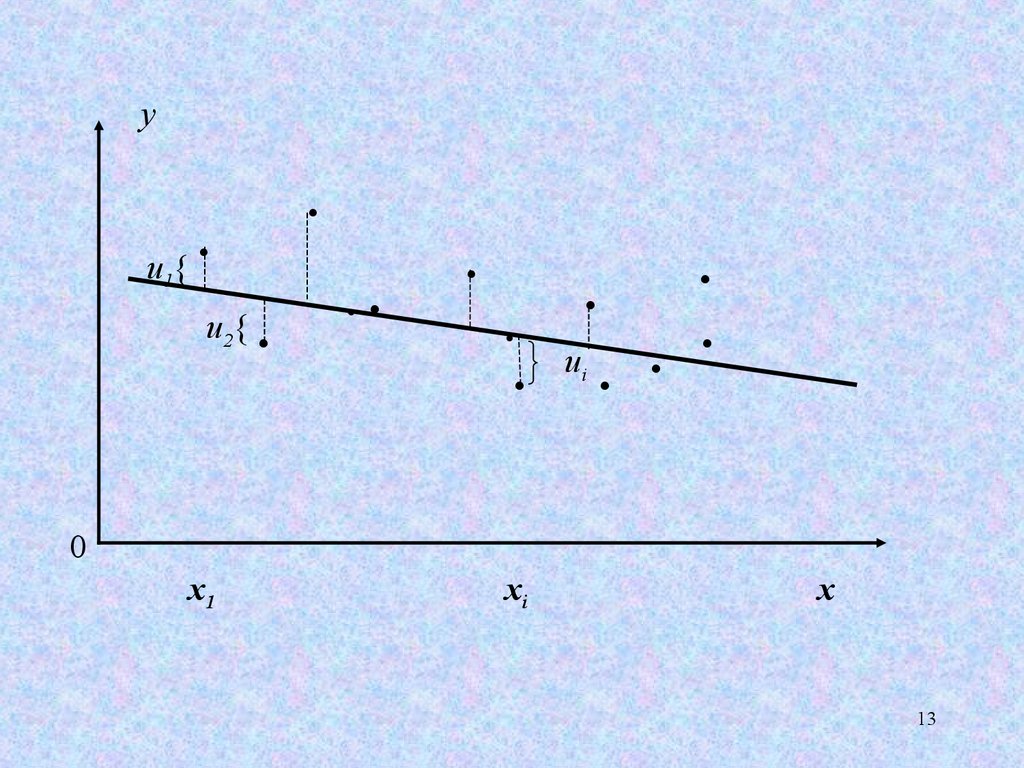
13.
y.
u{
1
u2{ .
.
..
.
.
.
.
.
. u. .
i
0
x1
xi
x
13
14.
nn
n
i 1
i 1
2
2
ˆ
u
Q
(
b
,
b
)
(
y
y
)
(
y
b
b
x
)
i
i i i 0 1 i min
0 1
2
i 1
Необхідною умовою існування мінімуму неперервно
диференційованої функції двох змінних є рівність нулю її
частинних похідних.
Так як
y
x;
b1
y
xi ;
b1 i
y
1;
b0
y
1;
b0 i
14
15.
nQ
b 2 yi b1 xi b0 xi 0
i 1
1
n
Q
2 yi b1 xi b0 0
b0
i 1
n
n
n 2
b1 xi b0 xi xi yi ;
i 1
i 1
i 1
n
n
b x b n y
1
i
0
i
i 1
i 1
15
16. Система нормальних рівнянь
b0 n b1 x y2
b0 x b1 x xy
16
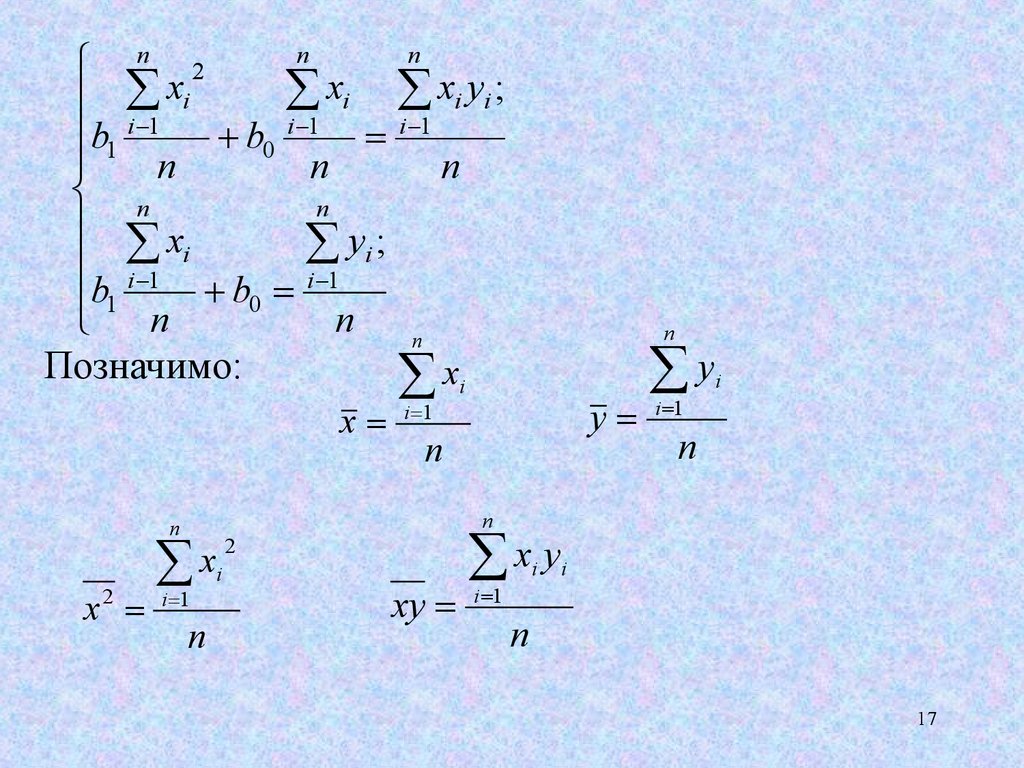
17.
nn
n 2
xi xi yi ;
xi
b0 i 1 i 1
b1 i 1
n
n
n
n
n
x
yi ;
i
i 1
i 1
b
b
0
1 n
n n
Позначимо:
xi
x
n
x2
xi
i 1
n
n
y
i 1
n
y
i 1
i
n
n
2
xy
x y
i
i 1
i
n
17
18.
одержимоb x 2 b x xy
1
0
b1x b0 y
звідки маємо
xy x y
b1 2
2
x x
b y b x
0
1
18
19.
Неважко помітити, щоза формулою:
b1
можна обчислити
n
b1
( xi x )( yi y )
i 1
n
( xi x )
2
S xy
S x2
i 1
S xy
1 n
cov( x, y ) ( xi x )( y i y ) -вибірковий кореляційний
n i 1
момент випадкових
величин X і Y;
19
20.
nn
1
1
2
2
2
S x ( xi x ) xi x 2 x 2 x 2
n i 1
n i 1
вибіркова дисперсія X
S x S x2
aˆ1
S xy
S
2
x
—стандартне відхилення X.
S xy
Sy
Sx S y Sx
rxy
Sy
Sx
rxy
—вибірковий коефіцієнт кореляції;
Sy
—стандартне відхилення Y.
20
21.
Коефіцієнт кореляціїrxy
S xy
Sx S y
xy x y
x x y y
2
2
2
2
0 rxy 1
21








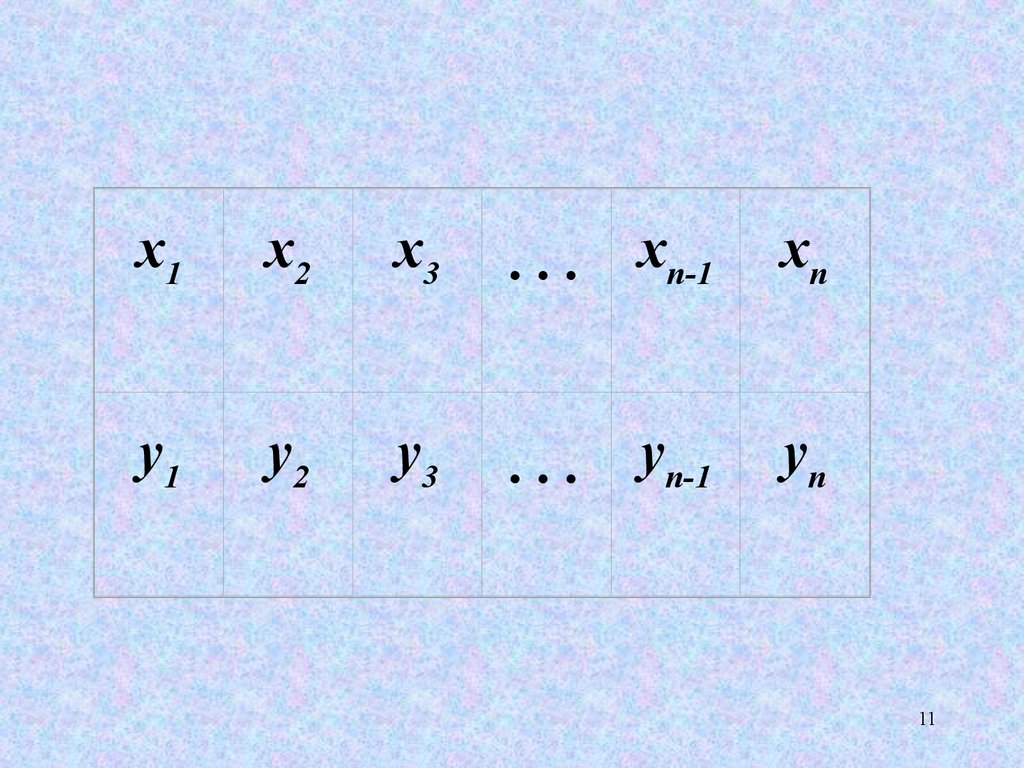



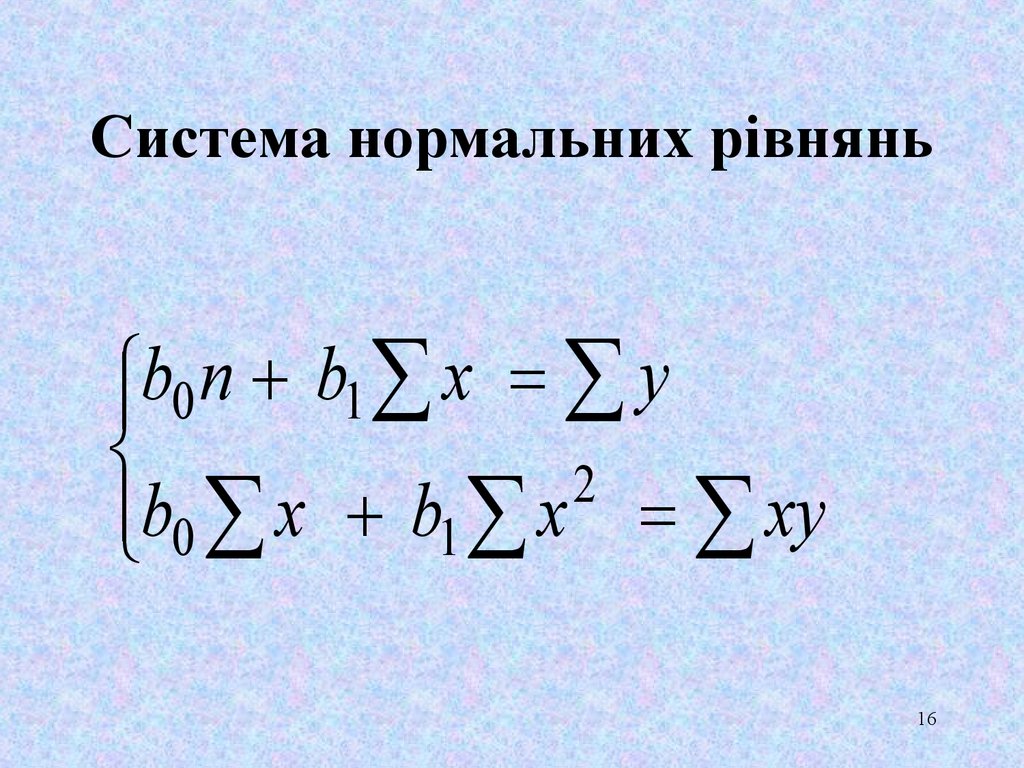




 Математика
Математика Экономика
Экономика








