Похожие презентации:
Роль і місце задач у початковому курсі математики
1.
1. Роль і місце задачу початковому
курсі математики.
2. Основною метою змістової лінії «Сюжетні задачі» є формування в учнів загального уміння працювати із задачею, умінь розв’язувати задачі п
Основною метою змістовоїлінії «Сюжетні задачі» є
формування в учнів загального
уміння працювати із задачею,
умінь розв’язувати задачі
певних типів.
3. Сюжетні задачі виступають важливим засобом:
• ілюстрації і конкретизації навчальногоматеріалу;
• розвитку пізнавальних процесів,
оволодіння прийомами розумової
діяльності;
• виховання вольових якостей,
естетичних почуттів;
• розвитку вміння будувати судження,
робити висновки;
• формування в учнів мотивації їхньої
навчальної діяльності, інтересу та
здатності до цієї діяльності.
4. Сюжетні задачі, особливо практично-зорієнтовані, забезпечують зв’язок математики із реальним життям дитини.
Сюжетні задачі,особливо практичнозорієнтовані,
забезпечують зв’язок
математики із реальним
життям дитини.
5.
У 1-му і 2-му класах формуютьпоняття про задачу (відповідно
просту або складену), її структурні
елементи, сутність процесу
розв’язування. Основним
завданням є набуття учнями
загального уміння розв’язувати
сюжетні задачі.
Уявлення про процес розв’язування
задачі формується як перехід від
текстової моделі (текст задачі) до
схематичної (короткий запис,
схема), а далі – до математичної
(вираз).
6. Задача – це комплексне математичне завдання, за допомогою якого можна перевірити знання та вміння учнів з різних тем початкового курсу ма
Задача – це комплексне математичнезавдання, за допомогою якого можна
перевірити знання та вміння учнів з
різних тем початкового курсу
математики
Математична задача – це будь-яка
вимога обчислити, побудувати, довести
що-небудь, що стосується кількісних
відношень і просторових форм,
створених людським розумом на основі
знань про навколишній світ
7. У системі навчання дітей початкових класів загальноосвітньої школи переважають арифметичні задачі.
Задачі на побудову, найпростішідоведення, завдання логічного
характеру займають порівняно
незначне місце
8. Арифметичною задачею називають вимогу знайти числове значення деякої величини, якщо дано числові значення інших величин та існує залежні
Арифметичною задачею називаютьвимогу знайти числове значення деякої
величини, якщо дано числові значення
інших величин та існує залежність, що
пов’язує ці величини як між собою, так і
з шуканою величиною.
9. У початкових класах в основному розглядаються так звані текстові (сюжетні) задачі.
Сюжетна задача – цематематична задача, де описано
певний життєвий сюжет, а саме
кількісний бік реальних
процесів, явищ та ситуацій, і
міститься вимога знайти
шукану величину за даними в
задачі величинами та зв’язками
між ними
10. Проста задача – сюжетна задача, на запитання якої можна відповісти одразу, виконавши 1 арифметичну дію. Складена задача – сюжетна задача, д
Проста задача – сюжетна задача,на запитання якої можна відповісти
одразу, виконавши 1 арифметичну
дію.
Складена задача – сюжетна задача,
для розв’язання якої необхідно
виконати 2 і більше арифметичні
дії.
11. За допомогою розв’язування простих задач в учнів формується одне з центральних понять початкового курсу математики – поняття про арифме
За допомогою розв’язуванняпростих задач в учнів формується
одне з центральних понять
початкового курсу математики –
поняття про арифметичні дії.
Уміння розв’язувати прості задачі є
підготовчим ступенем опанування
учнями умінь розв’язувати
складені задачі, бо розв’язування
складеної задачі зводиться до
розв’язування ряду простих задач.
12.
2. Функціїсюжетних задач.
13. Навчальні функції задач полягають у формуванні в учнів системи математичних знань, умінь і навичок на різних етапах її засвоєння
Задачі виступають засобомпереходу від операцій над
множинами, за допомогою яких у
дітей формуються первинні
уявлення про зміст
арифметичних дій, до дій над
натуральними числами
14.
Розв’язуючи задачі, учніусвідомлюють прикладне
значення математики,
усвідомлюють важливість
математичних знань для
пізнання закономірностей
навколишнього світу та
оволодівають практичними
вміннями і навичками, розуміють
зміст таких понять, як шлях і
швидкість, врожайність,
продуктивність праці тощо.
15. Текстові задачі мають великий виховний потенціал, оскільки сюжет задачі є моделлю реальної життєвої ситуації, близької дітям.
Крім того сам процес розв’язуваннязадачі сприяє вихованню у дітей
важливих якостей характеру –
наполегливості, старанності, уміння
переборювати труднощі, доводити
справу до кінця. Виховні функції
задач сприяють органічним зв'язкам
навчання з життям, виховують у
дітей свідоме ставлення до навчання,
бажання зробити власний внесок у
загальну справу
16. Сюжетні задачі мають значний розвивальний потенціал у процесі навчання молодших школярів
Під розвивальними розуміють функціїзадач, спрямовані на формування в
учнів науково-теоретичного, зокрема
функціонального стилю мислення,
на оволодіння цими прийомами
розумової діяльності. Реалізація будьякого етапу роботи над задачами
потребують від молодших школярів
актуалізації низки психічних
процесів: мислення, аналізу, синтезу,
порівняння, узагальнення тощо.
17.
3. Класифікаціяпростих задач.
18.
Прості задачі можна поділити нагрупи відповідно до
арифметичних дій, за
допомогою яких їх розв’язують.
Однак з погляду методики
зручніша інша класифікація –
поділ задач на групи залежно
від тих понять, які формують
під час їх розв'язування.
19. До першої групи належать прості задачі, під час розв'язування яких діти засвоюють конкретний зміст кожної з арифметичних дій, тобто засвою
До першої групи належать простізадачі, під час розв'язування яких діти
засвоюють конкретний зміст кожної
з арифметичних дій, тобто
засвоюють, яка арифметична дія
пов'язана з тією або іншою операцією
над множинами
20.
1) Знаходження суми двохчисел.
Дівчинка купила для ляльки 2
червоних і 3 зелених платтячка.
Скільки всього платтячок купила
дівчинка?
2) Знаходження остачі.
Андрійко намалював 6
малюнків. Два малюнки він
подарував учительці. Скільки
малюнків у нього залишилося?
21.
3) Знаходження суми однаковихдоданків (добутку).
У живому куточку жили кролі в
трьох клітках, по 2 кролі в
кожній. Скільки всього кролів у
живому куточку?
4) Поділ на рівні частини.
Два класи пропололи 8 грядок,
кожна порівну. Скільки грядок
пропололи школярі кожного
класу?
22.
5) Ділення на вміщення.Кожен клас школярів обкопав
по 6 кущів смородини, а всього
учні обкопали 18 кущів. Скільки
класів учнів виконували цю
роботу?
23. До другої групи належать прості задач під час розв'язування яких учні засвоюють зв'язок між компонентами і результатами арифметичних дій,
До другої групи належать простізадач під час розв'язування яких учні
засвоюють зв'язок між
компонентами і результатами
арифметичних дій, тобто задачі на
знаходження невідомих компонентів.
24.
1) Знаходження першого доданка завідомою сумою і другим доданком.
Дівчинка купила для ляльки кілька
червоних платтячок і 3 зелених, а
всього купила 5 платтячок. Скільки
червоних платтячок купила дівчинка?
2) Знаходження другого доданка за
відомою сумою і першим доданком.
Дівчинка купила для ляльки 2
червоних і кілька зелених платтячок,
усього вона купила 5 платтячок.
Скільки зелених платтячок купила
дівчинка?
25.
3) Знаходження зменшуваного завідомим від'ємником і остачею.
Андрійко намалював кілька
малюнків. Два малюнки він
подарував учительці, і в нього
залишилося ще 4 малюнки. Скільки
малюнків він намалював?
4) Знаходження від'ємника за
відомим зменшуваним і остачею.
Діти виготовили 6 шпаківень. Коли
кілька шпаківень вони повісили на
дереві, в них залишилось ще 4
шпаківні. Скільки шпаківень діти
повісили на дереві?
26.
5) Знаходження першогомножника за відомим добутком і
другим множником.
Кільком дітям роздали по 8 цукерок
і всі вони одержали 48 цукерок.
Скільком дітям дали цукерки?
6) Знаходження другого множника
за відомим добутком і першим
множником.
6 дітям роздали по кілька цукерок і
всі вони одержали 48 цукерок.
Скільки цукерок роздали кожній
дитині?
27.
7) Знаходження діленого завідомим дільником і часткою.
На день народження купили
кілька кексів і їх роздали 9 дітям по
3 кожному. Скільки кексів купили?
8) Знаходження дільника за
відомим діленим і часткою.
На день народження купили 27
кексів і їх роздали запрошеним
дітям по 3 кожному. Скільком
дітям роздали кекси?
28. До третьої групи належать задачі, під час розв'язування яких розкривають новий зміст арифметичних дій - задачі, пов'язані з поняттям різниц
До третьої групи належать задачі,під час розв'язування яких
розкривають новий зміст
арифметичних дій - задачі, пов'язані з
поняттям різниці і кратного
відношення.
29.
1) Різницеве порівняння чисел абознаходження різниці двох чисел
(перший вид).
Один будинок збудували за 10
тижнів, а другий - за 8 тижнів. На
скільки тижнів більше затратили на
будівництво першого будинку?
2) Різницеве порівняння чисел або
знаходження різниці двох чисел
(другий вид).
Один будинок збудували за 10
тижнів, а другий за 8. На скільки
тижнів менше затратили на
будівництво другого будинку?
30.
3) Збільшення числа на кількаодиниць (пряма форма).
Один будинок збудували за 8 тижнів,
а на будівництво другого будинку
затратили на 2 тижні більше. Скільки
тижнів затратили на будівництво
другого будинку?
4) Збільшення числа на кілька
одиниць (непряма форма).
Один будинок будували 8 тижнів, це
на 2 тижні менше, ніж будували
другий будинок. Скільки тижнів
будували другий будинок?
31.
5) Зменшення числа на кількаодиниць (пряма фірма).
Один будинок будували 10 тижнів, а
другий збудували на 2 тижні
швидше. Скільки тижнів будували
другий будинок?
6) Зменшення числа на кілька
одиниць (непряма форма).
Один будинок будували 10 тижнів, це
на 2 тижні більше, ніж будували
другий будинок. Скільки тижнів
будували другий будинок?
32.
4. Ознайомленняучнів з простою
задачею.
33. Ознайомлення з простою задачею починається у першому класі і передбачає:
• читання задач;• знання структурних елементів
задачі – умова і запитання;
числові дані та шукане;
• розуміння, що в умові задачі
містяться числові дані, а
запитання вказує на шукане;
• визначення числових даних,
необхідних і достатніх для
відповіді на запитання задачі;
34. Ознайомлення з простою задачею починається у першому класі і передбачає:
• робити висновок про те, чиописана ситуація є задачею
• розв’язування простих задач на
знаходження суми, різниці двох
чисел; збільшення та
зменшення числа на кілька
одиниць, різницеве порівняння;
знаходження невідомого
доданка
35. Ознайомлення з простою задачею починається у першому класі і передбачає:
• виділяє умову і запитання, прокого або про що йдеться в
задачі, числові дані й шукане;
• обґрунтовування вибору
арифметичної дії для
розв’язування задачі;
• записування розв’язання задачі
дією із зазначенням
найменування результату,
коротку відповідь;
36. Ознайомлення з простою задачею продовжується у другому класі і передбачає:
• узагальнення і систематизаціюнавчального матеріалу за 1-й клас
• розуміння, що один і той самий
вираз може бути розв’язанням
безлічі сюжетних задач;
• обґрунтовування усного вибору
арифметичної дії, якою
розв’язується задача;
37. Ознайомлення з простою задачею продовжується у другому класі і передбачає:
• розв’язування задачі назнаходження третього числа за
сумою двох інших, на
знаходження суми трьох
доданків, на розкриття суті
множення, ділення, на
збільшення або зменшення числа
в кілька разів, на кратне
порівняння чисел.
38.
Під час розв’язуванняпростих задач акцент
ставиться на
обґрунтуванні вибору
арифметичної дії,
необхідної для відповіді на
запитання задачі; під час
розв’язування складених –
на аналітичних або
синтетичних міркуваннях
щодо пошуку плану
розв’язування.
39.
• Для розв’язування сюжетнихзадач переважно обирається
арифметичний метод.
• Розв’язування задачі
арифметичним методом
записують діями з
поясненням до кожної із них
або за допомогою виразу.
• Цим забезпечується єдність
виконання розумових дій
аналізу і синтезу.
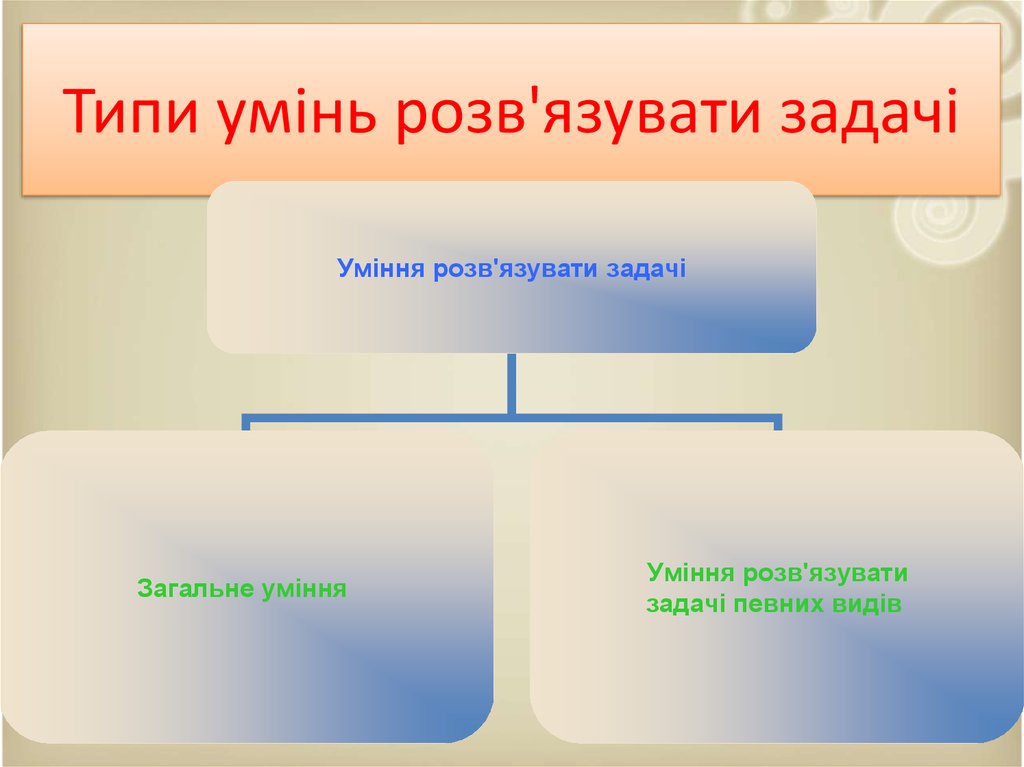
40. Типи умінь розв'язувати задачі
Уміння розв'язувати задачіЗагальне уміння
Уміння розв'язувати
задачі певних видів
41. Загальне уміння розв'язувати задачі (складне уміння, що застосовується при розв’язуванні сюжетної задачі різними (основними) методами та
Загальне уміння розв'язувати задачі (складнеуміння, що застосовується при розв’язуванні
сюжетної задачі різними (основними) методами
та способами)
1. уміння здійснювати предметно-змістовий аналіз задачі;
2.уміння виконувати логіко-семантичний аналіз задачі;
3.уміння складати репрезентативну модель задачі
(короткий запис задачі у вигляді схеми або таблиці; або
малюнок, схематичний рисунок, креслення, діаграму,
графік тощо);
4.уміння робити прикидку очікуваного результату;
5.уміння здійснювати пошук розв’язування задачі: за
арифметичного способу – виконувати аналітичні або
синтетичні міркування; за алгебраїчного – позначати одне
з невідомих значень величини (шукане або проміжне)
змінною та виражати інші величини через змінну,
подавати одну з величин двома способами (через змінну
та без неї);
42.
6. уміння складати план розв’язування задачі за арифметичногоспособу; за алгебраїчного – уміння складати рівняння;
7. уміння реалізувати знайдений план розв’язування за
арифметичного способу; за алгебраїчного – уміння
розв’язувати рівняння;
8. уміння перевіряти правильність розв’язання;
9. уміння співвідносити нову задачу з раніше розв’язаними;
перетворювати дану задачу; узагальнювати математичну
структуру задачі;
10.уміння досліджувати задачу шляхом змін окремих її елементів
– з метою формулювання загального плану розв’язування
задач такої самої математичної структури.
43.
5. Методиканавчання учнів
розв’язувати
прості задачі.
44. 1) ознайомлення з задачею
1) ознайомлення з задачею
пояснення незнайомих термінів робиться заздалегідь, щоб не
відволікатися на це під час
розбору задачі;
сприймання тексту задачі зі слів
вчителя чи самостійно;
виділення кожної смислової
одиниці тексту, відбувається
шляхом читання тексту задачі
частинами;
перевірка усвідомлення змісту
задачі.
45.
• Організувати ознайомлення іззадачею можна по-різному.Учні
повинні прочитати чи прослухати
задачу не менше 2 разів, коли задача
нового виду – то і 3-4 рази.
Наприклад, 1-й раз – читає вчитель, 2
– учні самостійно; 3 раз – 1 учень
переказує.
• У 1 і 2 класах задачу читає, переказує
вчитель, у 3 і 4 – учні
ознайомлюються здебільшого
самостійно, крім випадку, коли
задача нового виду і вчителю
необхідно зробити при читанні
логічні акценти.
46. 2) аналіз тексту задачі
• усвідомлення зв'язків міжвеличинами, через відтворення
реальної ситуації, моделлю якої є
дана задача;
• вербальний розбір задачі
здійснюється двома основними
способами або синтетичним (від
числових даних до запитання) або
аналітичним (від запитання до
числових даних).
47. 3) пошук розв'язування задачі
• вибір арифметичної дії, зобов'язковим обґрунтуванням
цього вибору, двома способами
– усно або письмово
48. 4) реалізація плану розв'язування задачі – відповіді на поставлені питання плану
49. 5) запис розв'язання і відповіді
• заповнення ланцюга логічнихміркувань прикладами, тобто
виконання арифметичних дій
відповідно складеного плану
розв'язування
50. 6) робота над задачею після її розв'язання передбачає співставлення даних з результатом, повідомлення правильної відповіді вчителем
51.
6. Класифікаціяскладених задач.
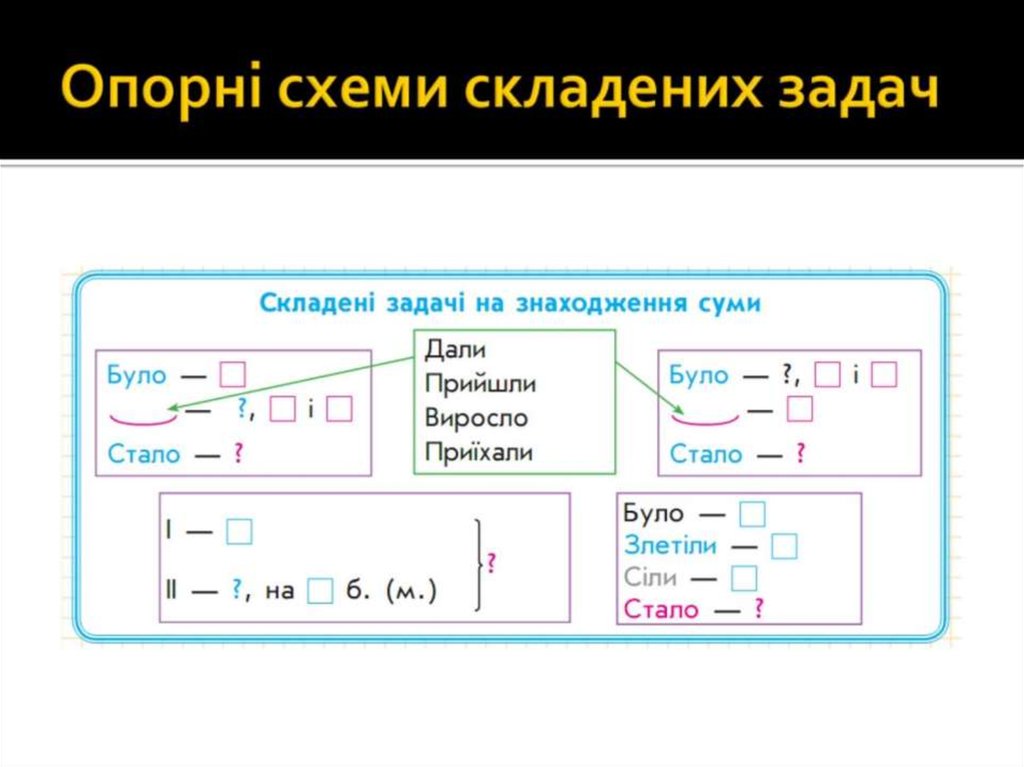
52. Опорні схеми складених задач
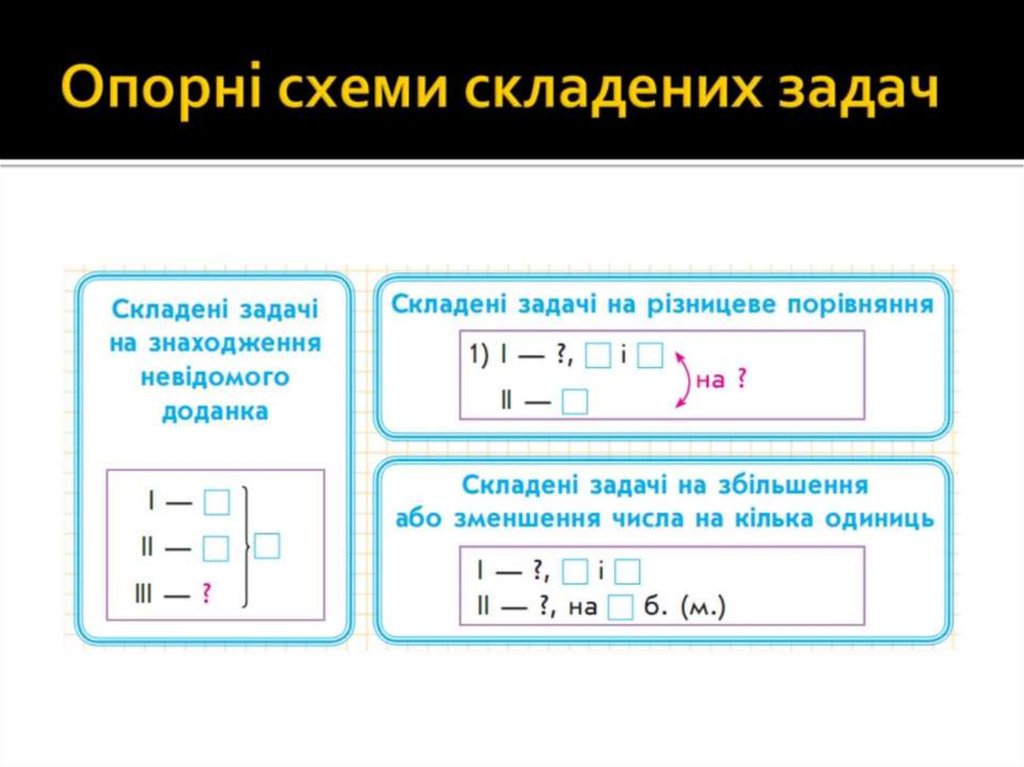
53. Опорні схеми складених задач
54. Опорні схеми складених задач
55.
7. Види ілюстраціїзмісту складеної
задачі.
56. Ілюстрування змісту задачі допомагає учням виокремити величини, про які йдеться у задачі і усвідомити зв’язки між ними.
57. - предметна (за допомогою предметів чи їх зображень); - малюнкова; - короткий запис (структурний, табличний, графічний).
58. Предметна
Оксанка з Іринкою обриваличерешні. Оксанка зірвала 10
черешень, а Іринка тільки 6.
Скільки черешень обірвали
сестрички?
59. Малюнкова
Маса гарбуза 12 кг, а диня на 9 кгменша. У скільки разів маса
гарбуза більша за масу дині?
60. Короткий запис (структурний)
Оксанка з Іринкою обривали черешні.Оксанка зірвала 10 черешень, а Іринка
тільки 6. Скільки черешень обірвали
сестрички?
Оксанка – 10 ч.
? ч.
Іринка – 6 ч.
Оксанка з Іринкою обривали черешні.
Оксанка зірвала 10 черешень, а Іринка
тільки на 3 менше. Скільки черешень
обірвали сестрички?
Оксанка – 10 ч.
? ч.
Іринка – ?, на 3 ч. <
61. Короткий запис (табличний)
На пошиття восьми простираделшвачка витратила 2м тканини, а
на пошиття шести підковдр 4 м.
Скільки метрів тканини
витратила швачка на пошиття
усіх виробів?
62. Короткий запис (графічний)
63.
8. Культура записурозв’язання задачі.
64. На кінець 1-го класу
У тарілці було 5 слив, мамапоставила туди ще 4 сливи.
Скільки слив стало у тарілці?
65. На кінець 1-го класу
Довжина рожевої стрічки 9сантиметрів, а блакитна на 4
сантиметри коротша. На
скільки сантиметрів рожева
смужка довша?
66. У 3-му класі
Школярі посади 19 яблунь. Напершій ділянці посадили 4
яблуні, на другій – 7, а решту на
третій. Скільки яблунь
посадили на третій ділянці?
67. У 3-му класі
Школярі посади 19 яблунь. Напершій ділянці посадили 4
яблуні, на другій – 7, а решту на
третій. Скільки яблунь
посадили на третій ділянці?
68.
9. Задачі назнаходження
четвертого
пропорційного.
Задачі на пропорційне
ділення.
69. Задачі на знаходження четвертого пропорційного – це задачі, в яких говориться про три величини, одна з яких стала, а дві інші – змінні; дано
два значенняоднієї змінної величини і одне з
відповідних значень другої
змінної, а друге відповідне
значення потрібно знайти.
70. Існує 6 видів цього типу задач. У початкових класах такі задачі розв'язуються способом прямого та оберненого зведення до одиниці і способом
відношень.71. Підготовча робота включає розв'язування простих задач із пропорційними величинами: ціна, кількість, вартість; маса одного предмета, кількі
Підготовча робота включаєрозв'язування простих задач із
пропорційними величинами:
ціна, кількість, вартість; маса
одного предмета, кількість
предметів, загальна маса; норма
витрати на один виріб, кількість
виробів, загальна витрата тощо.
72. Підготовча робота включає розв'язування простих задач із пропорційними величинами: ціна, кількість, вартість; маса одного предмета, кількі
Підготовча робота включає розв'язування простихзадач із пропорційними величинами: ціна, кількість,
вартість; маса одного предмета, кількість предметів,
загальна маса; норма витрати на один виріб, кількість
виробів, загальна витрата тощо.
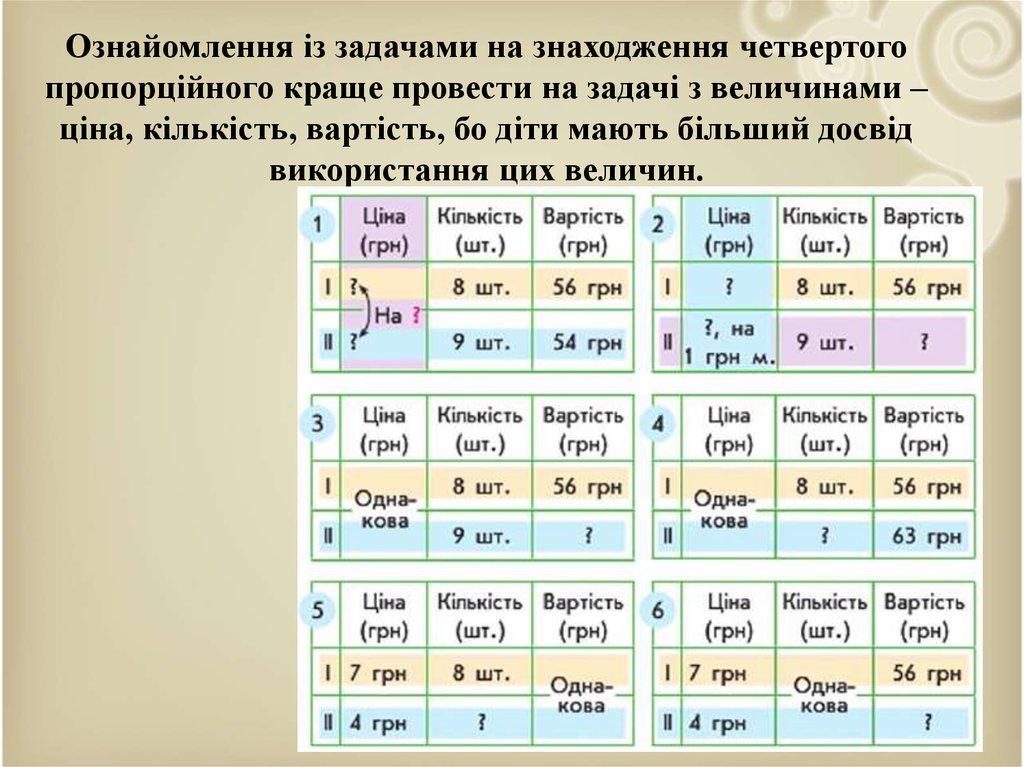
73. Ознайомлення із задачами на знаходження четвертого пропорційного краще провести на задачі з величинами – ціна, кількість, вартість, бо ді
Ознайомлення із задачами на знаходження четвертогопропорційного краще провести на задачі з величинами –
ціна, кількість, вартість, бо діти мають більший досвід
використання цих величин.
74.
75. Можна розпочати з готової задачі. Задача. Купили 6 книг за однаковою ціною і заплатили 42 грн. Потім купили ще 4 книги за тією ж ціною. Скільки
Можна розпочати з готової задачі.Задача. Купили 6 книг за однаковою ціною і
заплатили 42 грн. Потім купили ще 4 книги за тією
ж ціною. Скільки гривень коштують 4 книги?
Щоб підкреслити, що ціна однакова, короткий запис можна подати
табличним способом:
76. - Чи можемо одразу знайти вартість 4-ох книг? - Чому? А що сказано про ціну кожної з чотирьох книг? (Однакова з ціною кожної з 6 книг.) - Чи можемо
Після вивчення задачі приступаємо допошуку плану розв'язування:
- Чи можемо одразу знайти вартість 4-ох книг?
- Чому?
А що сказано про ціну кожної з чотирьох книг?
(Однакова з ціною кожної з 6 книг.)
- Чи можемо знайти ціну кожної з 6-ти книг?
Складаємо план розв'язування задачі і записуємо
розв'язання, пояснюючи вибір кожної дії.
Для первинного закріплення учні розв'язують задачу
самостійно, опираючись на короткий запис і план
розв'язування.
77.
78. За поживністю 3 кг ячменю замінюють 4 кг вівса. Скільки кілограмів ячменю потрібно, щоб замінити 12 кг вівса? На дошці запис: Для кращого осмис
У 4-ому класі знайомство учнів з розв'язуванням задач назнаходження 4-ого пропорційного способом відношень.
За поживністю 3 кг ячменю замінюють 4 кг вівса.
Скільки кілограмів ячменю потрібно, щоб замінити 12
кг вівса?
На дошці запис:
Для кращого осмислення задачі її можна
проілюструвати графічно:
!!! З кожних 10 м однакової тканини шиють 3
плаття. Скільки таких плать можна пошити з 50 м
тканини?
Розглянувши ілюстрацію, приступаємо до аналізу
задачі:
79.
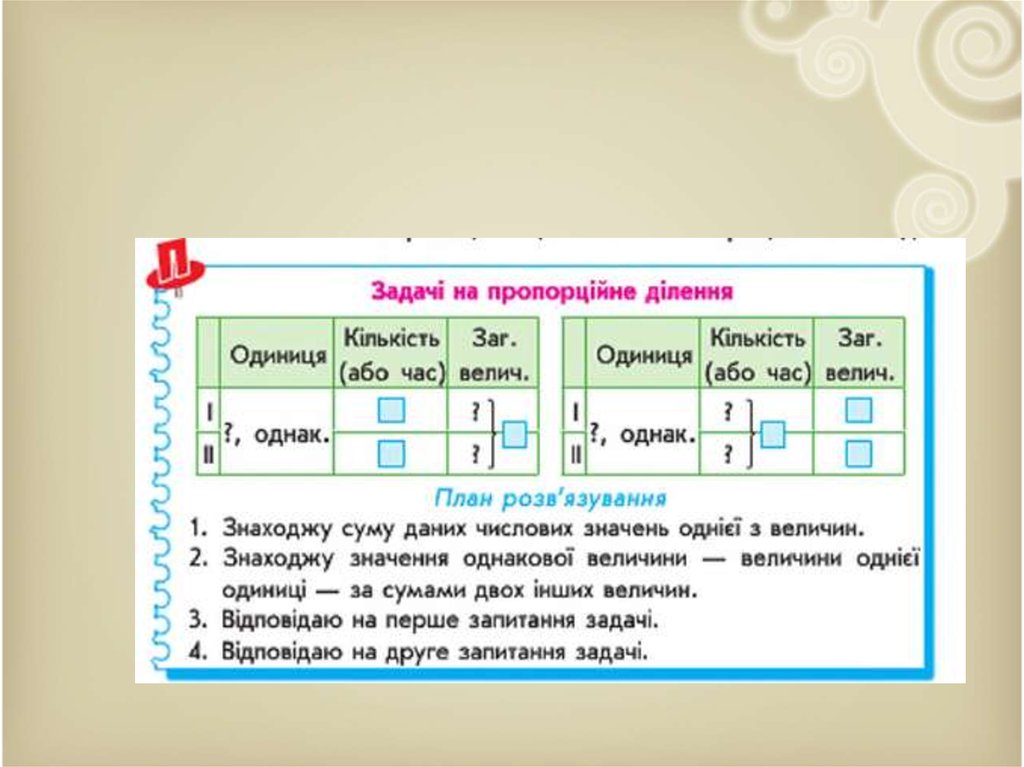
80. Задачі на пропорційне ділення – це задачі, в яких говориться про три величини, одна з яких стала, а дві змінні: дано 2 значення однієї змінно
Задачі на пропорційне ділення –це задачі, в яких говориться про
три величини, одна з яких стала, а
дві змінні: дано 2 значення однієї
змінної і сума відповідних значень
іншої змінної, а відповідні
значення треба знайти.
81. У початкових класах розглядають 4 види задач на пропорційне ділення (лише з малопропорційною залежністю між змінними). Підготовкою до розв'
У початкових класах розглядають 4види задач на пропорційне ділення
(лише з малопропорційною
залежністю між змінними).
Підготовкою до розв'язування задач на
пропорційне ділення є добре вміння
розв'язувати задачі на знаходження
четвертого пропорційного.
82.
83.
84.
85.
86.
10. Задачі назнаходження
невідомого за двома
різницями.
Задачі на
знаходження
середнього
арифметичного.
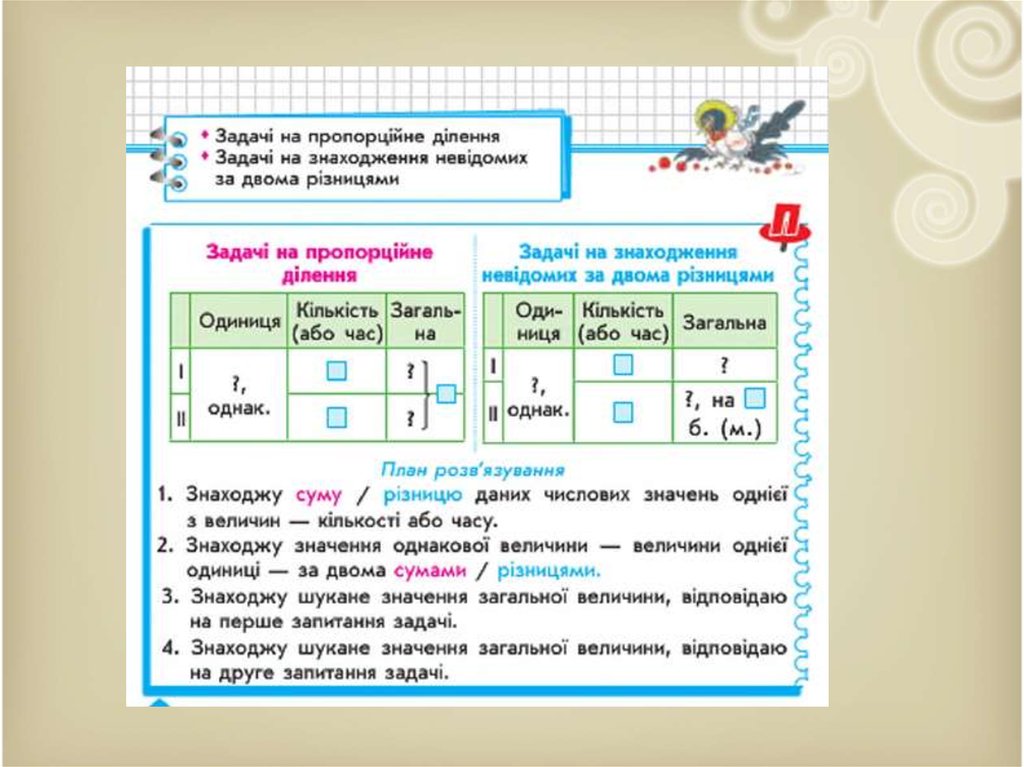
87. Задачі на знаходження невідомого за двома різницями – це задачі, в яких говориться про три величини, одна з яких стала, а дві – змінні: дано
Задачі на знаходження невідомогоза двома різницями – це задачі, в
яких говориться про три величини,
одна з яких стала, а дві – змінні: дано
два значення однієї змінної і різниця
відповідних значень другої змінної, а
відповідні значення треба знайти.
88.
Підготовчівправи.
89.
90.
91. Задачі на знаходження середнього арифметичного Розв'язування цих задач ґрунтується на правилі: щоб знайти середнє арифметичне кількох чи
Задачі на знаходження середньогоарифметичного
Розв'язування цих задач ґрунтується на правилі:
щоб знайти середнє арифметичне кількох
чисел, треба їх суму поділити на кількість цих
чисел.
Задачі цього типу застосовуються для
знаходження середньої швидкості, маси,
урожайності тощо.
Аналіз цих задач можна проводити як і
нетипових: синтетичним, повним чи неповним
аналітичним або аналітико-синтетичним
способами.
92.
93.
11. Задачі на рух.94. Задачі на рух (одночасний рух двох тіл назустріч або у протилежних напрямках). Ці задачі виділено в окремий тип завдяки специфіці сюжету. Їх
особливість проявляється більше у підготовчійроботі, тому при ознайомленні зі швидкістю та
співвідношенням між швидкістю, часом і відстанню
треба розкрити такі поняття, як "одночасність" руху,
рухи "назустріч" і "в протилежних напрямках",
"швидкість зближення", "швидкість віддалення" та
форми схематичного короткого запису задач. Аналіз
задач на рух проводиться так само, як і нетипових.
95.
96.
97.
98.
99.
12. Види творчоїроботи над задачею
100. Повторне розв'язування задач.
• Якщо задачу повторно розв'язуютьвідразу після запису останньої дії і
відповіді, то це буде момент первинного
закріплення.
• Тут мається на увазі повторне
розв'язування через деякий час, тобто
через кілька днів або тижнів.
• Цей прийом не належить безпосередньо
до творчої роботи, але він відіграє певну
роль при формуванні і закріпленні вмінь
розв'язувати задачі.
101. Зміна числових даних
Пропонують розв'язати задачу, аналогічну дорозв'язаних на попередніх уроках, але з
іншими числовими даними. Здебільшого
змінюють одне з даних.
У першій бригаді 7 сівалок, а в другій — на 2
сівалки менше. Скільки сівалок в обох
бригадах?
Завдання:
а) розв'язати таку саму задачу, але щоб в ній
було сказано, що в другій бригаді на 4 сівалки
більше;
б) розв'язати задачу, але число 7 замінити
іншим числом;
в) розв'язати задачу, але числові дані замінити
так, щоб шукане число збільшилось.
102. Зміна запитання
Застосування цього прийому наголошує наспрямовуючій ролі запитання для вибору
необхідних зв'язків і стимулює учнів до
всебічного аналізу задачної ситуації. Зміну
запитання використовують також для
постановки нових задач, її "розширення".
У першій каністрі 18 л бензину, а в другій —6 л.
Скільки літрів бензину в двох каністрах?
Завдання:
а) на скільки літрів бензину в першій каністрі
більше, ніж у другій?
б) у скільки разів менше бензину в другій
каністрі, ніж у першій?
в) скільки літрів бензину потрібно долити, щоб
в каністрах бензину стало порівну?
103. Зміна сюжету задачі
Пропонують розв'язати таку самузадачу, але з іншими величинами.
При цьому учні вчаться з'ясовувати
умови застосування в реальній
дійсності тих чи інших залежностей
104. Зміна, деяких зв'язків
Такий прийом привертає увагу дітей дозначення окремих слів і виразів у контексті
задачі. Вони поступово усвідомлюють, що
незначні на перший погляд зміни ведуть до
істотних змін у ході розв'язування, роблять
висновок про можливість зміни характеру
залежностей між величинами.
Убілки 12 горіхів, а в хом 'яка — на 3 горіхи
менше. Скільки горіхів у білки і хом 'яка
разом?
Завдання.
Замінити в умові вираз "на 3 горіхи менше"
іншим — "у 3 рази менше" ("на 3 горіхи
більше", "у 3 рази більше") і розв'язати задачу
105. Поступове ускладнення умови задачі
Спочатку учням пропонують кілька зміненихзадач, в яких збільшується кількість числових
даних, включаються додаткові зв'язки, а
запитання задачі залишається без змін. Що дає
змогу бачити, як ускладнення числових даних і
зв'язків впливає на хід розв'язування задач.
Турист за день пройшов 10 км і проїхав на
автобусі 180 км. Скільки кілометрів пройшов і
проїхав турист за день?
1. Турист ішов 2 год по 5 км/год та їхав на автобусі
180 км.
2. Турист ішов 2 год по 5 км/год та їхав 3 год
автобусом зі швидкістю 60 км/год.
3. Пішки турист ішов 2 год, а автобусом їхав на 1
год більше. Він ішов зі швидкістю 5 км/год, а
їхав в автобусі зі швидкістю 60 км/год.
106. Розв'язування задач різними способами.
Деякі арифметичні задачі допускають двачи кілька способів розв'язування. Такі
задачі є ефективним навчальним
матеріалом, на основі якого в учнів
пробуджується допитливість,
самостійність мислення. Намагання
знайти інший шлях розв'язування тієї
самої задачі сприяє підвищенню
емоційного стану школярів.




































































































 Математика
Математика Педагогика
Педагогика








