Уравнения Максвелла. Лекция 16

1.

Уравнения Максвелла.
Переменный ток.
Иллюстративный материал к
лекции №16
пятница, 16 июня 2023 г.

2.

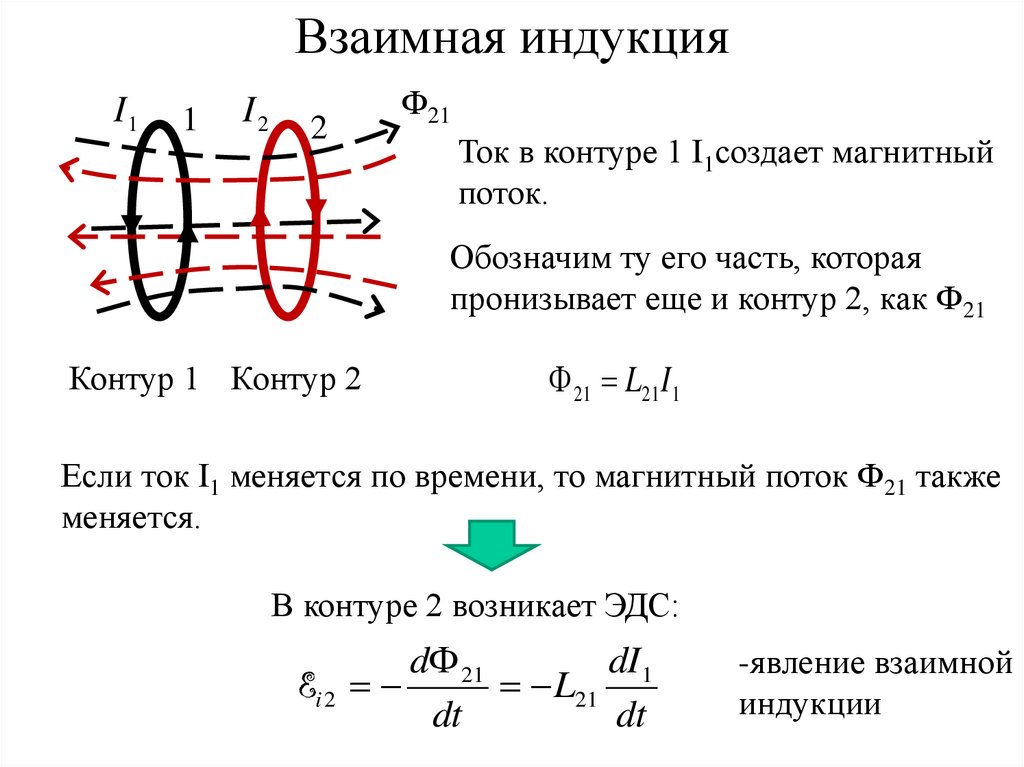
Взаимная индукция
I1
1
I2
2
Ф21
Ток в контуре 1 I1создает магнитный
поток.
Обозначим ту его часть, которая
пронизывает еще и контур 2, как Ф21
Контур 1 Контур 2
21 L21 I1
Если ток I1 меняется по времени, то магнитный поток Ф21 также
меняется.
В контуре 2 возникает ЭДС:
d 21
dI1
Ei 2
L21
dt
dt
-явление взаимной
индукции

3.

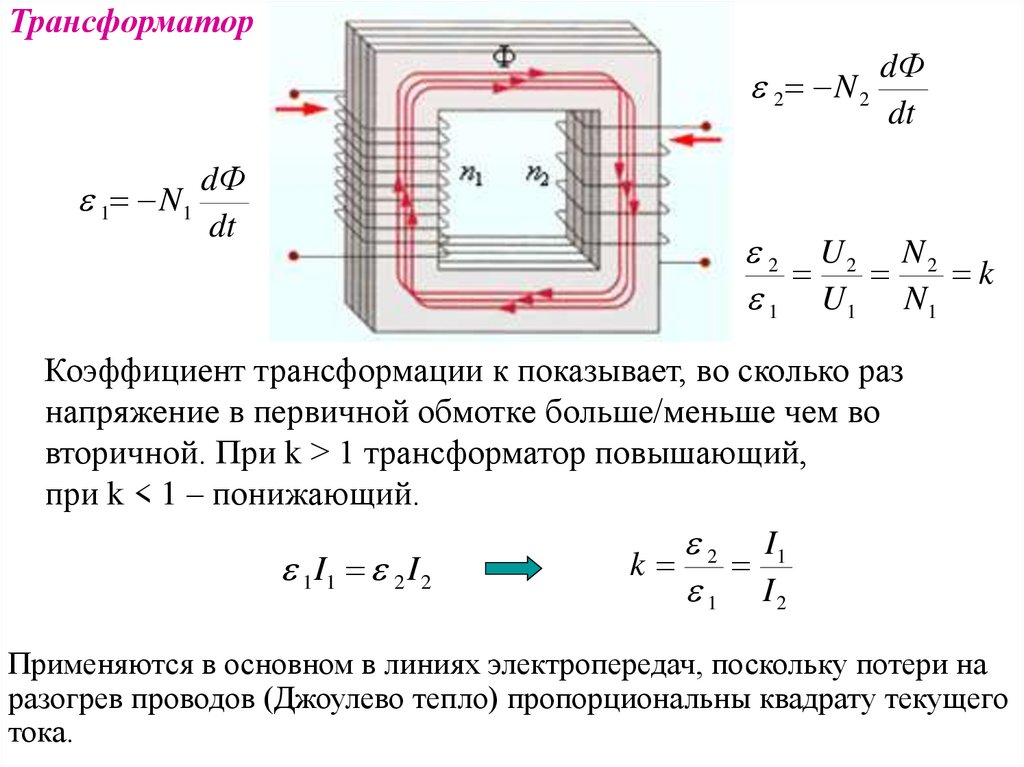
Трансформатор
dФ
2 N 2
dt
dФ
1 N1
dt
2 U2 N2
k
1 U1 N 1
Коэффициент трансформации к показывает, во сколько раз
напряжение в первичной обмотке больше/меньше чем во
вторичной. При k > 1 трансформатор повышающий,
при k < 1 – понижающий.
2 I1
k
1I1 2 I 2
1 I2
Применяются в основном в линиях электропередач, поскольку потери на
разогрев проводов (Джоулево тепло) пропорциональны квадрату текущего
тока.

4.

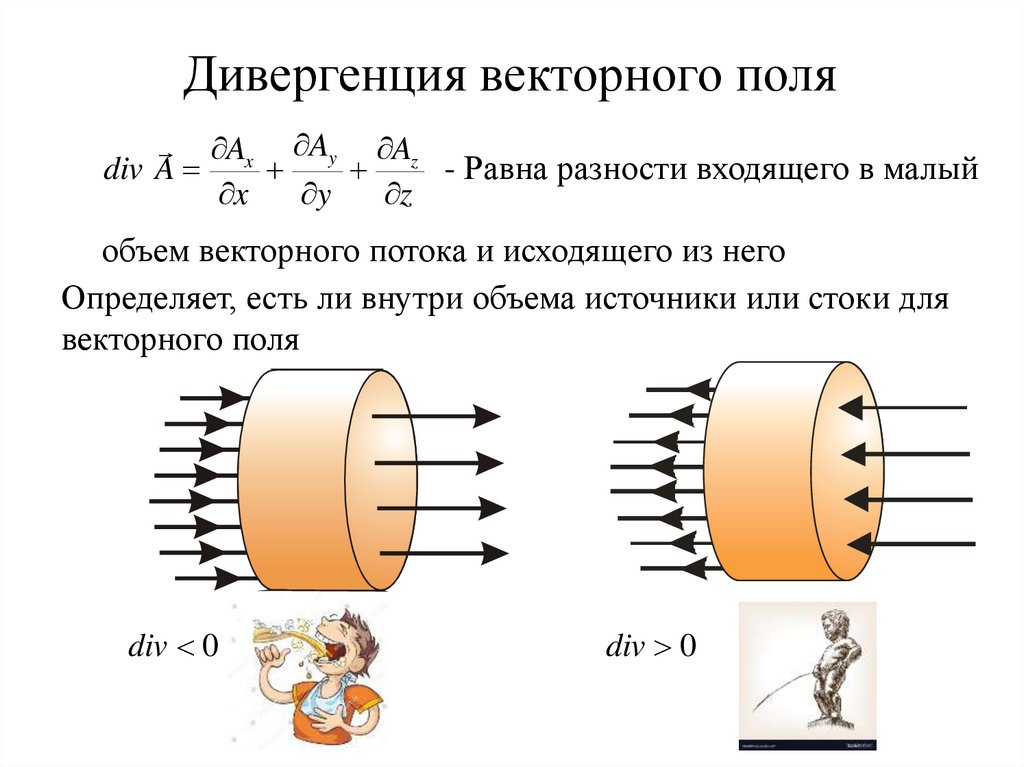
Дивергенция векторного поля
Ax Ay Az
- Равна разности входящего в малый
div A
x
y
z
объем векторного потока и исходящего из него
Определяет, есть ли внутри объема источники или стоки для
векторного поля
div 0
div 0

5.

Дивергенция векторного поля
x
z
z
y
x
Вычислим поток вектора А:
Ax x2 Ax x1 y z
Ay y2 Ay y1 x z
Az z 2 Az z1 x y
y
Будем уменьшать поверхность S:
lim Ax x2 Ax x1 y z Ay y2 Ay y1 x z Az z2 Az z1 x y
S 0
Ax Ay Az
Ax Ay Az
x y z
V
y
z
y
z
x
x
AdS divAdV - Теорема Остроградского-Гаусса
S
V

6.

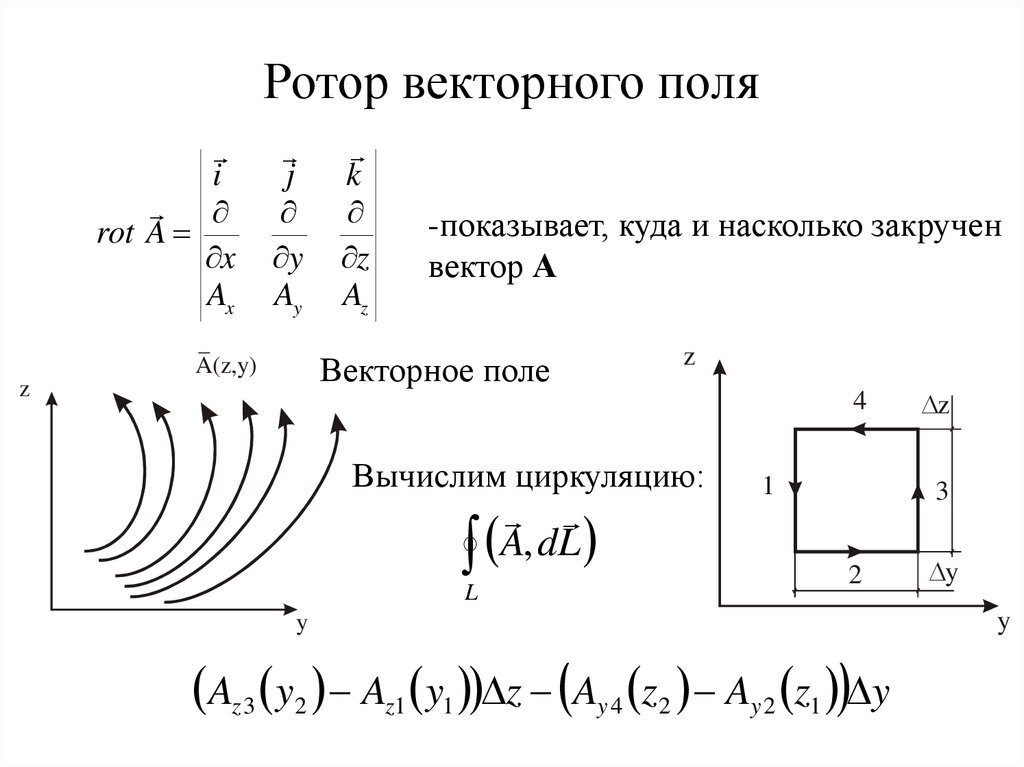
Ротор векторного поля
i
rot A
x
Ax
j
y
Ay
k
z
Az
-показывает, куда и насколько закручен
вектор А
Векторное поле
A(z,y)
z
z
4
Вычислим циркуляцию:
A, dL
L
1
z
3
2
y
Az 3 y2 Az1 y1 z Ay 4 z2 Ay 2 z1 y
y
y

7.

Ротор векторного поля
Az 3 y2 Az1 y1 z Ay 4 z2 Ay 2 z1 y
Будем уменьшать размеры контура L
lim Az 3 y2 Az1 y1 z Ay 4 z2 Ay 2 z1 y
z , y 0
Ay
Az Ay
Az
y z
z y
y z
y
z
z
y
Az Ay
S
z
y
Теорема Стокса
Adl rotAdS
L
S

8.

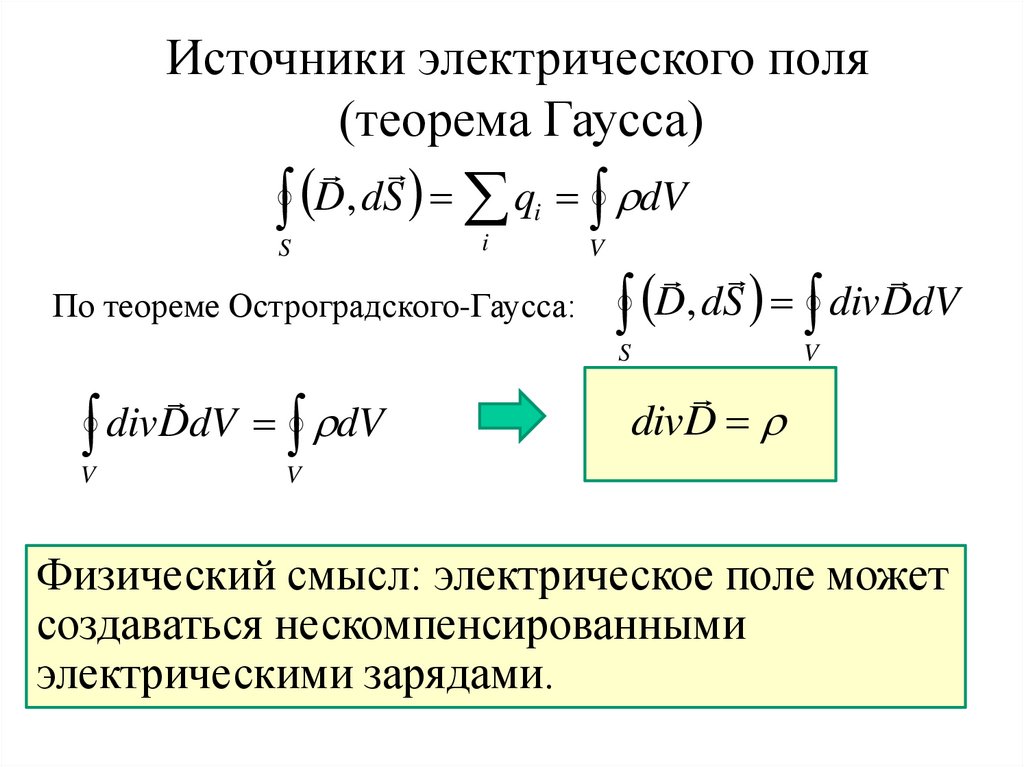
Источники электрического поля
(теорема Гаусса)
D, dS qi dV
S
i
V
По теореме Остроградского-Гаусса: D, dS div DdV
S
divDdV dV
V
V
divD
V
Физический смысл: электрическое поле может
создаваться нескомпенсированными
электрическими зарядами.

9.

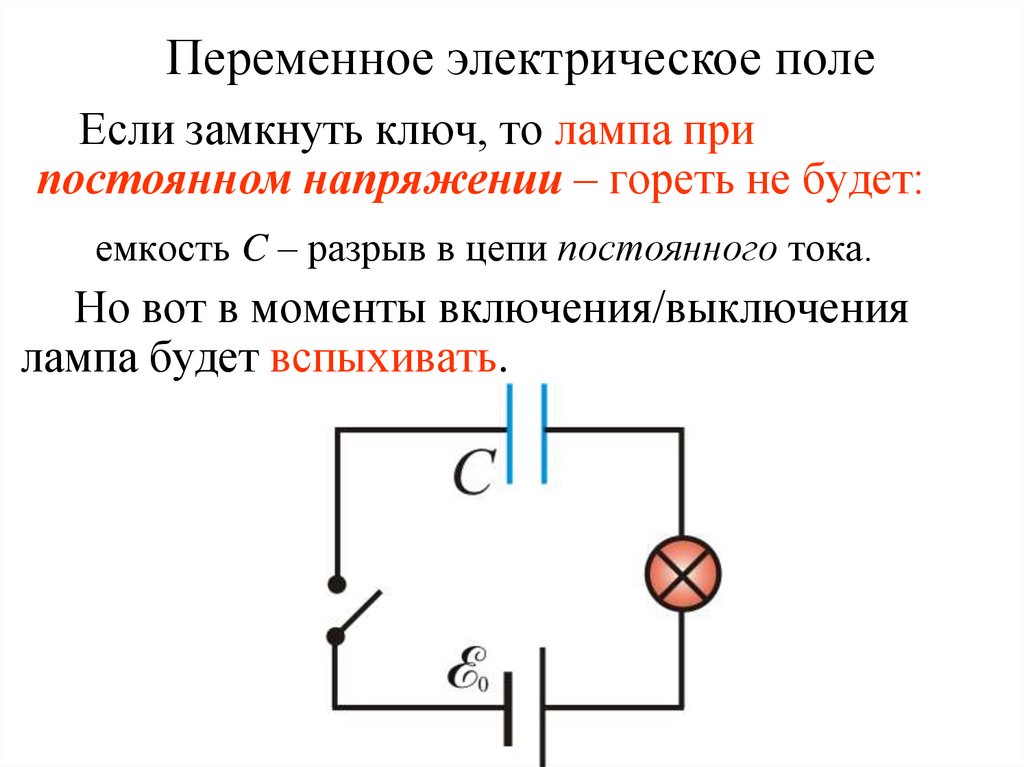
Переменное электрическое поле
Если замкнуть ключ, то лампа при
постоянном напряжении – гореть не будет:
емкость C – разрыв в цепи постоянного тока.
Но вот в моменты включения/выключения
лампа будет вспыхивать.

10.

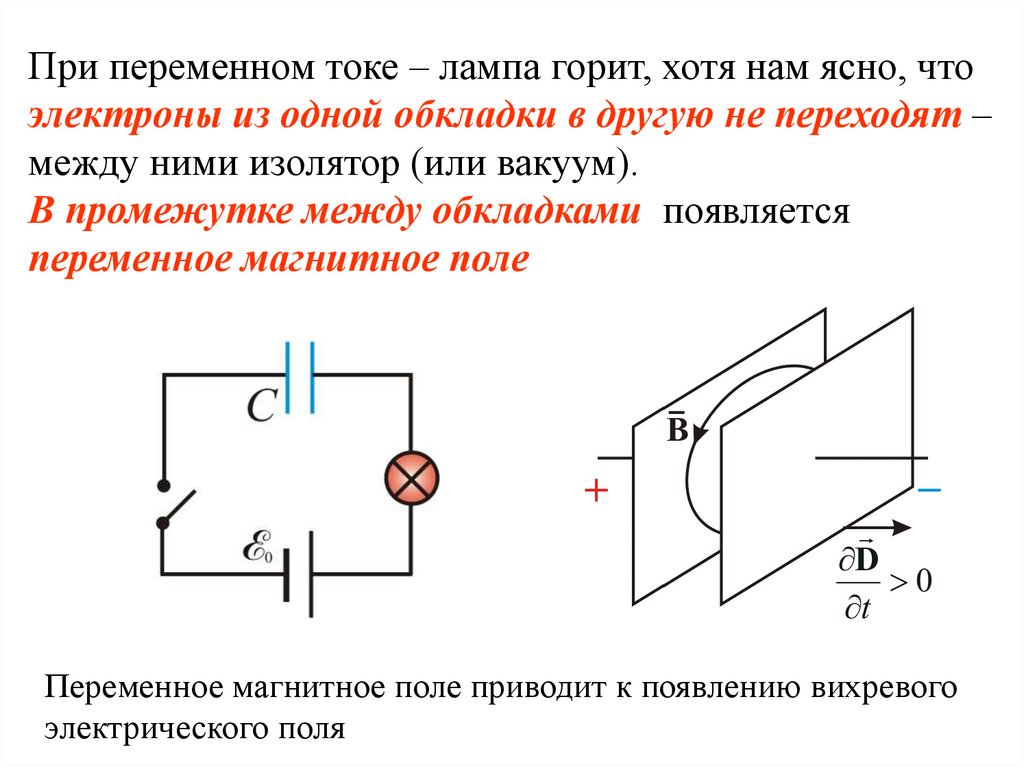
При переменном токе – лампа горит, хотя нам ясно, что
электроны из одной обкладки в другую не переходят –
между ними изолятор (или вакуум).
В промежутке между обкладками появляется
переменное магнитное поле
Переменное магнитное поле приводит к появлению вихревого
электрического поля

11.

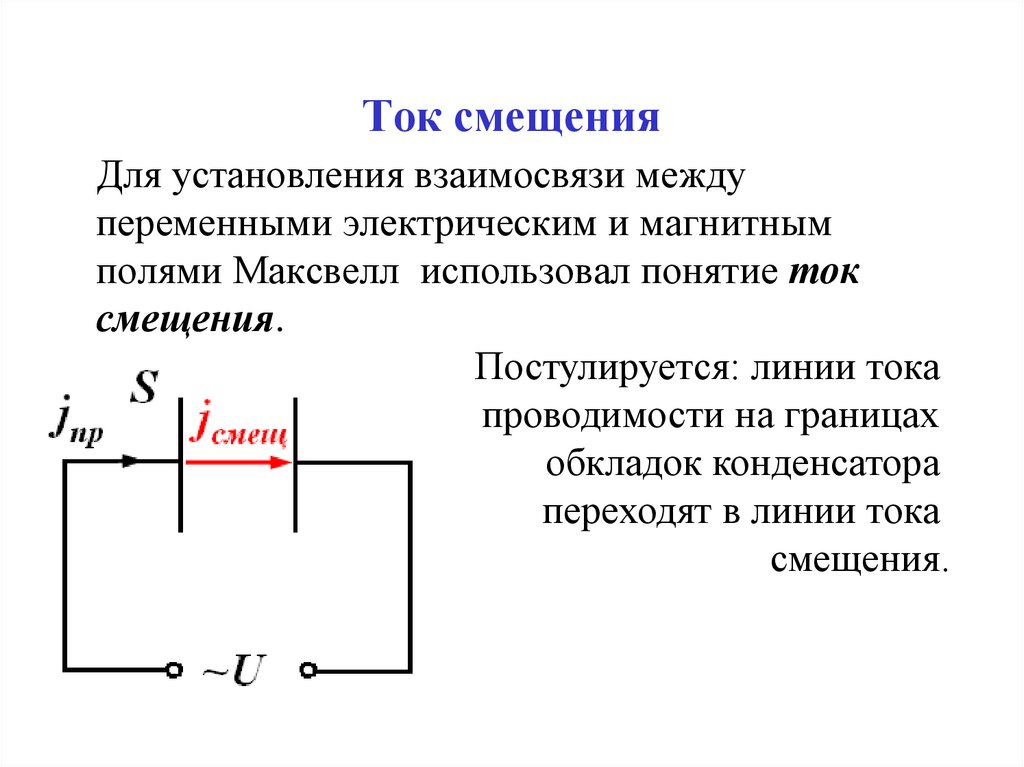
Ток смещения
Для установления взаимосвязи между
переменными электрическим и магнитным
полями Максвелл использовал понятие ток
смещения.
Постулируется: линии тока
проводимости на границах
обкладок конденсатора
переходят в линии тока
смещения.

12.

Ток смещения
jпр jсм -плотность тока смещения равна плотности тока
в проводе
I
jпр
S
- плотность тока в проводе
dq
I
dt
- изменение заряда на обкладках конденсатора
q S
- величина заряда на обкладках конденсатора
S - площадь
поверхностная плотность заряда

13.

Ток смещения
Ток в проводе:
d
I S
dt
I d
jсм
S dt
Электрическое
поле в конденсаторе
Вектор смещения
E
0
dD
jсм
dt
dD
jсм
dt
D 0E
Ток смещения равен скорости изменения вектора электрического
смещения

14.

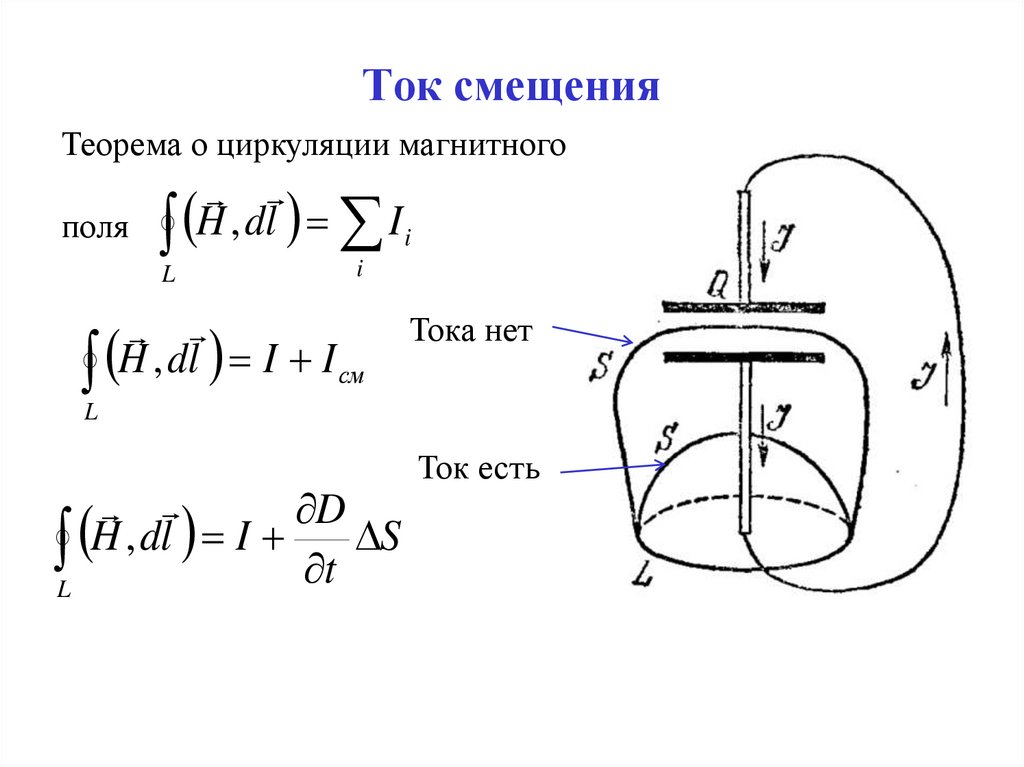
Ток смещения
Теорема о циркуляции магнитного
поля
H , dl I i
L
i
H , dl I I см
Тока нет
L
D
L H , dl I t S
Ток есть

15.

Ток смещения
Запишем циркуляцию через плотности токов:
D
D
L H , dl I t S S J t dS
По теореме Стокса:
H , dl rotHdS
L
S
D
Получаем:
S rotHdS S J t dS
Физический смысл: магнитное поле
D
порождается током проводимости и
rotH J
t
переменным электрическим полем.

16.

Переменное магнитное поле
dФ
Поток: Ф B, dS
ЭДС индукции: i
dt
S
i E , dl ЭДС равна циркуляции вихревого
L
электрического поля
B
L E, dl t S B, dS S t , dS
По теореме Стокса:
E , dl rotEdS
L
B
S rotEdS S t , dS
S
B
rotE
t

17.

Переменное магнитное поле
B
rotE
t
Физический смысл: Описывает возникновение вихревого
электрического поля под действием переменного магнитного
поля.
Содержит закон Фарадея и правило Ленца

18.

Вид силовых линий магнитного поля
BdS 0
div B 0
S
Поток вектора индукции В магнитного поля
через любую замкнутую поверхность равен
нулю.
Следовательно, силовые линии магнитного
поля замкнуты.

19.

Переменный ток ток, изменяющийся во времени по величине и направлению
(по синусоидальному закону).
Период (Т) - Наименьший промежуток времени,
через который периодически изменяющаяся
величина повторяется по форме и величине
f
f .
a(t)=Amsin( t + )
Am – максимальное значение, или амплитуда (Im);
t+ – фаза (фазовый угол);
– начальная фаза (начальный фазовый угол);
– угловая частота.

20.

• Действующие значения переменных токов, напряжений,
э.д.с:
T
1 2
I
i (t )d t
T 0
Средние значения переменных токов, напряжений, э.д.с за
положительную полуволну:
T
1 2
I СР
i (t )d t
T 0
2

21.

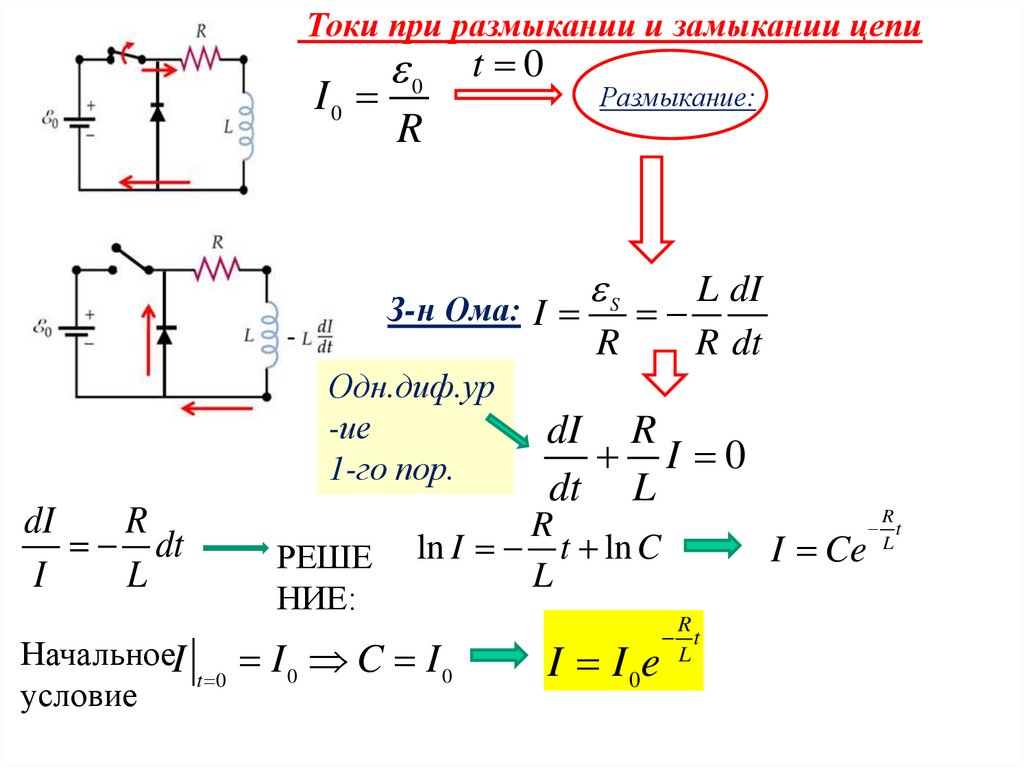
Токи при размыкании и замыкании цепи
I0
0
t 0
Размыкание:
R
З-н Ома: I
Одн.диф.ур
-ие
1-го пор.
dI
R
dt
I
L
РЕШЕ
НИЕ:
S
L dI
R
R dt
dI R
I 0
dt L
R
ln I t ln C
L
НачальноеI
I0 C I0
t 0
условие
I I 0e
I Ce
R
t
L
R
t
L

22.

R
t
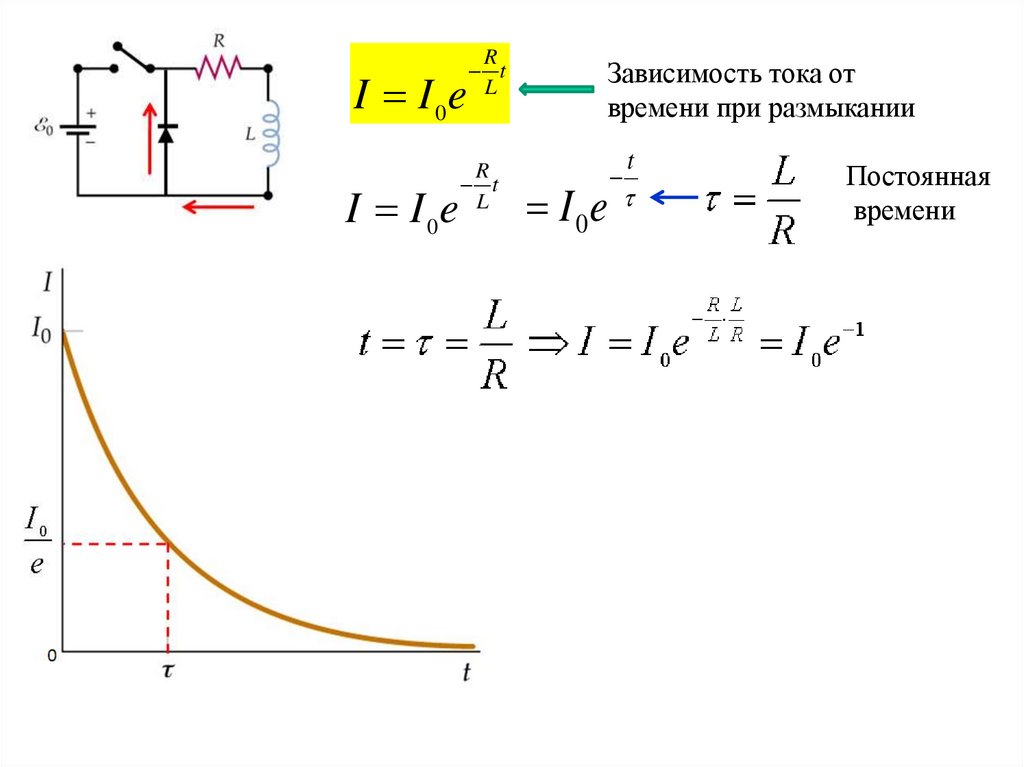
L
Зависимость тока от
времени при размыкании
R
t
L
I I 0e
I I 0e
I 0e
t
Постоянная
времени

23.

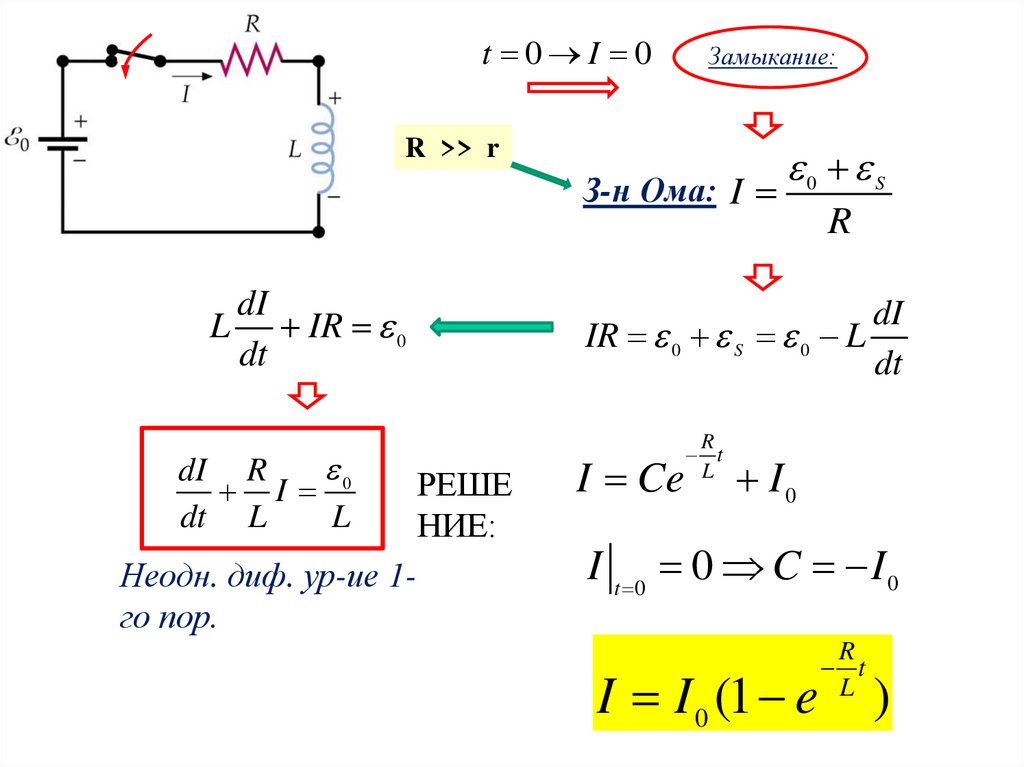
t 0 I 0
Замыкание:
R >> r
З-н Ома: I
dI
L IR 0
dt
0
dI R
I
dt L
L
Неодн. диф. ур-ие 1го пор.
0 S
R
dI
IR 0 S 0 L
dt
РЕШЕ
НИЕ:
I Ce
R
t
L
I0
I t 0 0 C I 0
I I 0 (1 e
R
t
L
)

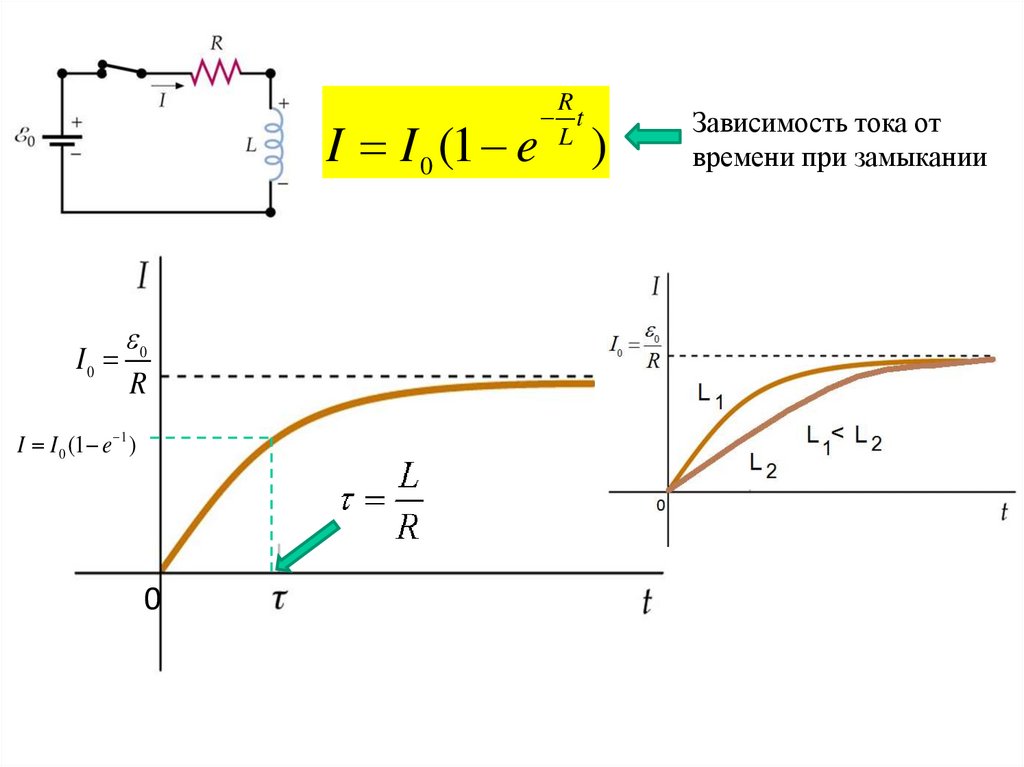
24.

I I 0 (1 e
I0 0
R
I I 0 (1 e 1 )
0
R
t
L
)
Зависимость тока от
времени при замыкании

25.

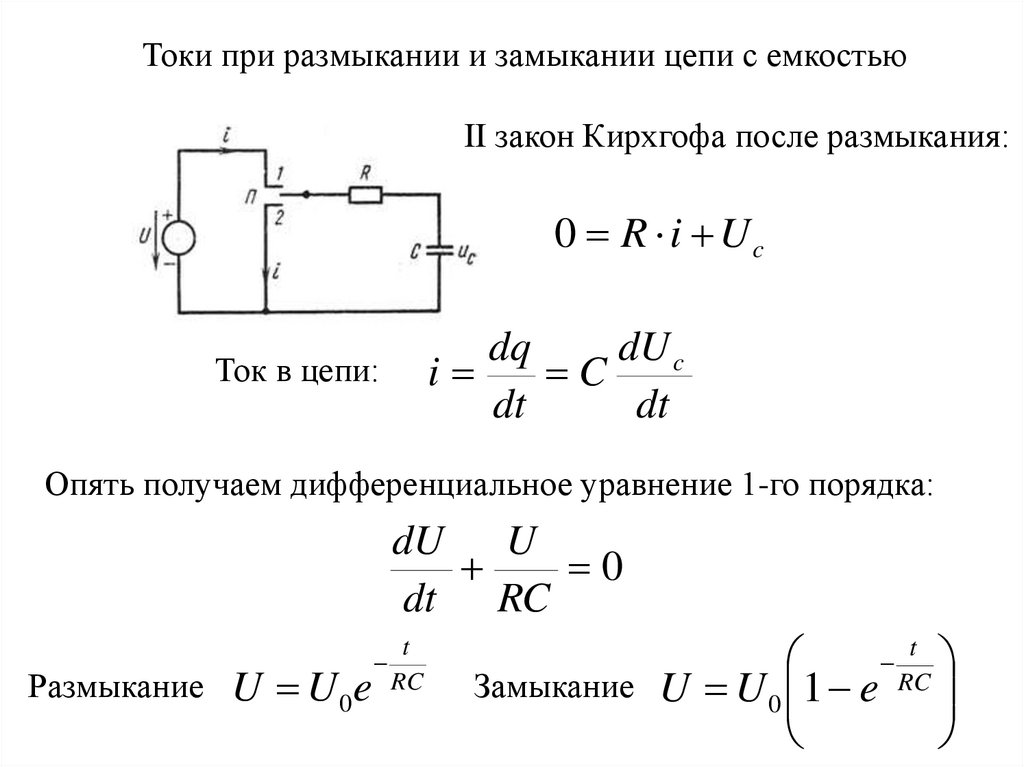
Токи при размыкании и замыкании цепи с емкостью
II закон Кирхгофа после размыкания:
0 R i Uc
dq
dU c
i
C
dt
dt
Ток в цепи:
Опять получаем дифференциальное уравнение 1-го порядка:
dU U
0
dt RC
Размыкание
U U 0e
t
RC
t
RC
Замыкание U U 0 1 e