Похожие презентации:
Основы оптимального приёма сигналов
1. 3. Основы оптимального приёма сигналов
3.1. Оптимальная оценка параметра сигнала3.2. Оптимальное обнаружение сигнала
3.3. Оптимальное различение известных сигналов
3.4.
Оптимальная обработка сигналов с
использованием согласованных фильтров
2.
Основные понятияОптимальный приёмник устройство обработки, обеспечивающее
наилучшее выделение полезной информации из сигнала, принимаемого в
смеси с аддитивной шумовой помехой
Шумовая помеха нормальный белый шум
Синтез оптимального приёмника нахождение структуры и
параметров устройства обработки, обеспечивающее наилучшее
выделение полезной информации из определённого типа сигнала
Критерий оптимальности приёмника правило, которое определяет,
какой способ выделения полезной информации считается наилучшим
Примеры:
- критерий минимума СКО
- критерий максимума отношения сигнал-шум
- критерий максимума апостериорной вероятности
1
3.
Будут рассмотреныЗадачи, решаемые в теории оптимального
приёма сигналов
1. Оценка параметров сигнала, принимаемого в смеси с
помехами
2. Обнаружение сигнала на фоне помех
3. Различение двух или нескольких сигналов на фоне помех
4. Фильтрация (выделение) сигнала из смеси с помехами
(Задачи 2 и 3 – частный случай задачи 1)
2
4.
3.1. Оптимальная оценкапараметра сигнала
Априорная и апостериорная вероятности
a priori «из предыдущего» (до «опыта»)
a posteriori «из последующего» (после «опыта»)
Принимаемая смесь сигнала и шума:
y (t ) = s (t ) + n(t )
До начала обработки известно (априорная информация):
•вид сигнала
•распределение вероятностей шума
•априорное распределение вероятностей параметра
Обрабатываются:
r r
r
N отсчётов (вектор) принятого колебания: y = ( y1 , y2 ,K , y N ) = s + n
или
непрерывное колебание:
y (t ) = s (t ) + n(t )
3
5.
Формула полной вероятностиСовместная
r плотность вероятности
отсчётов y = ( y1 , y2 ,K , y N ) и параметра
r
r
r = w( | y ) × w(y )
w( , y )
= w(yr | ) × w( )
r
r
r
Þ w( | y ) × w(y ) = w(y | ) × w( )
r
r
w(y | ) = L( ) условная плотность вероятности отсчётов y при
условии, что параметр равен (функция правдоподобия)
w( ) = wpr ( ) априорная плотность вероятности параметра
r
параметра
w( | y ) = wps ( ) апостериорная плотность вероятности
r
при условии, что приняты отсчёты y
r
r
w(y ) плотность вероятности отсчётов y
4
6.
Формула Байеса. Функция правдоподобия1
wps ( ) = r L( ) wpr ( ) = c1 L( ) wpr ( )
w(y )
r
Функция правдоподобия L( ) = w(y | ) = w( y1 , y2 ,K , y N | )
условная плотность вероятности отсчётов принятой
смеси сигнала и шума, рассматриваемая как функция
параметра
5
7.
Функция правдоподобия параметра сигнала,принимаемого на фоне нормального белого шума
1-й шаг: находим функцию правдоподобия в случае шума с ограниченным спектром
Условия :
а) спектр шума ограничен частотой f в ,
дисперсия шума s2 = G0вf
r
б) отсчёты y = ( y1 , y2 ,K , y N ) берутся с частотой
f д = 2 f в (по теореме Котельникова)
Получаем L( ) = w( y1 , y2 ,K , y N | )
2-й шаг: увеличивая fв , переходим к пределу:
f в ® ¥ Þ G ( f ) белый шум, дисперсия шума s 2 ® ¥
r
f д ® ¥, N ® ¥ Þ y ® y (t ) непрерывное колебание
Получаем L( ) = w( y (t ) | )
6
8.
Функция правдоподобия при конечной частоте fвfв
АКФ шума с граничной частотой
¥
fв
0
0
K (t) = ò G ( f ) cos 2pf t df = G0 ò cos 2pf t df =
= G0вf
sin 2pf в t
sin 2pf в t
= s2
2pf в t
2pf в t
1
,
Отсчёты шума, взятые с интервалом дискретизации Dtд = 1 f д =
2 fв
некоррелированы и статистически независимы (т.к. имеют
нормальное распределение) . Следовательно,
N
L( ) = w( y1 , y2 ,K , y N | ) = w( y1 | ) × w( y2 | ) × K × w( y N | ) = Õ w( yi | )
i =1
7
9.
Функция правдоподобия при конечной частоте fвНормальное распределение вероятностей отсчётов:
8
10.
Функция правдоподобия приL( ) = c2 ec3 × e q ( ) × e
fв ® ¥
Ec ( )
G0
9
11.
Апостериорная плотность вероятности параметраи её логарифм
w ps ( ) = c1 × L( ) × w pr ( ) = c1c2 e c3 × e q ( ) × e
Ec ( )
G0
× w pr ( ) = C e q ( ) e
Ec ( )
G0
w pr ( )
Логарифм апостериорной плотности вероятности параметра:
æ q ( ) EcG( )
ö
E ( )
ln wps ( ) = ln ç Ce e 0 wpr ( ) ÷ = ln C + q( ) c
+ ln w pr ( )
ç
÷
G0
è
ø
T
2
q ( ) =
y (t ) s (t ) dt корреляционный интеграл
ò
G0 0
T
Eс ( ) = ò s 2 (t )dt энергия сигнала
0
Оценка параметра по критерию максимума апостериорной вероятности:
ˆ = argmax w ps ( ) = argmax ln wps ( )
10
12.
Оценка параметра полностью известного сигнала(корреляционный приёмник)
11
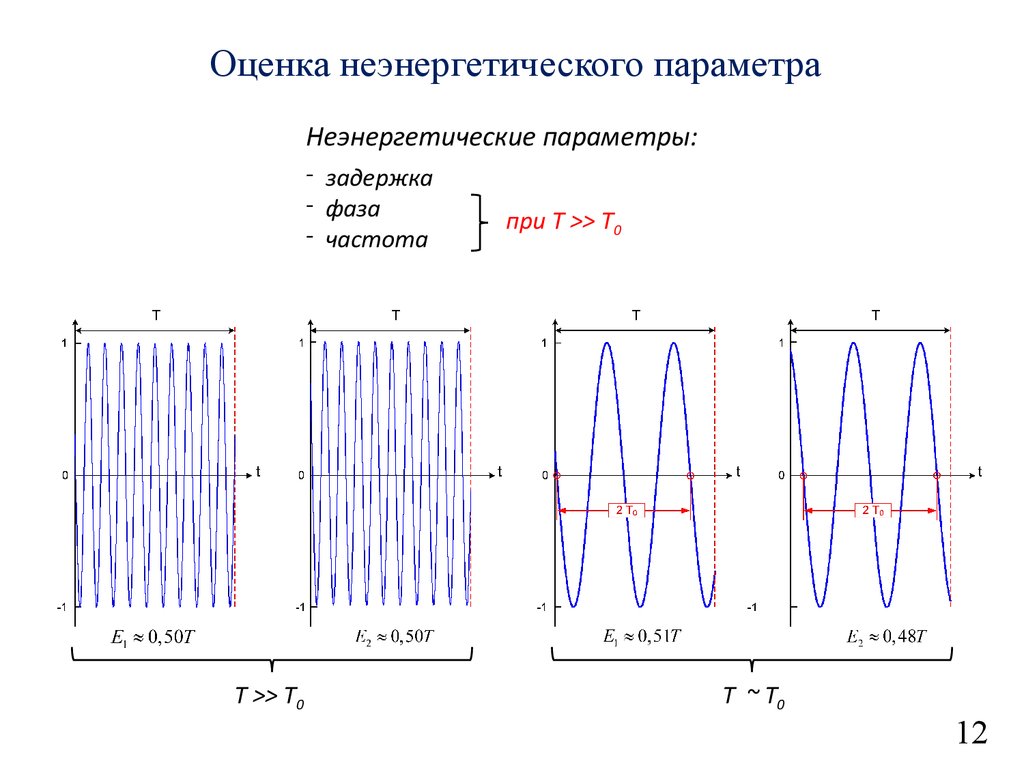
13.
Оценка неэнергетического параметраНеэнергетические параметры:
- задержка
- фаза
- частота
T >> T0
при T >> T0
T ~ T0
12
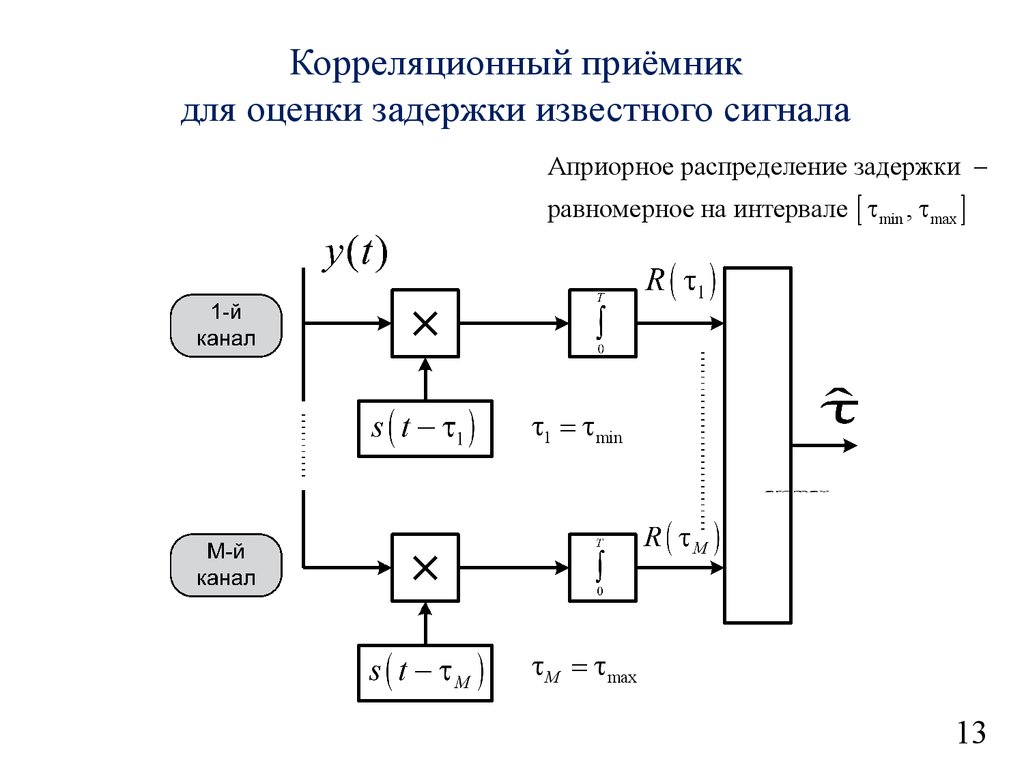
14.
Корреляционный приёмникдля оценки задержки известного сигнала
Априорное распределение задержки
равномерное на интервале [ tmin , tmax ]
t1 = tmin
tM = tmax
13
15.
Эпюры напряжений в корреляционном приёмникепрямоугольного видеоимпульса
mˆ = argmax R (tm )
m =1, M
tˆ = tmˆ
14
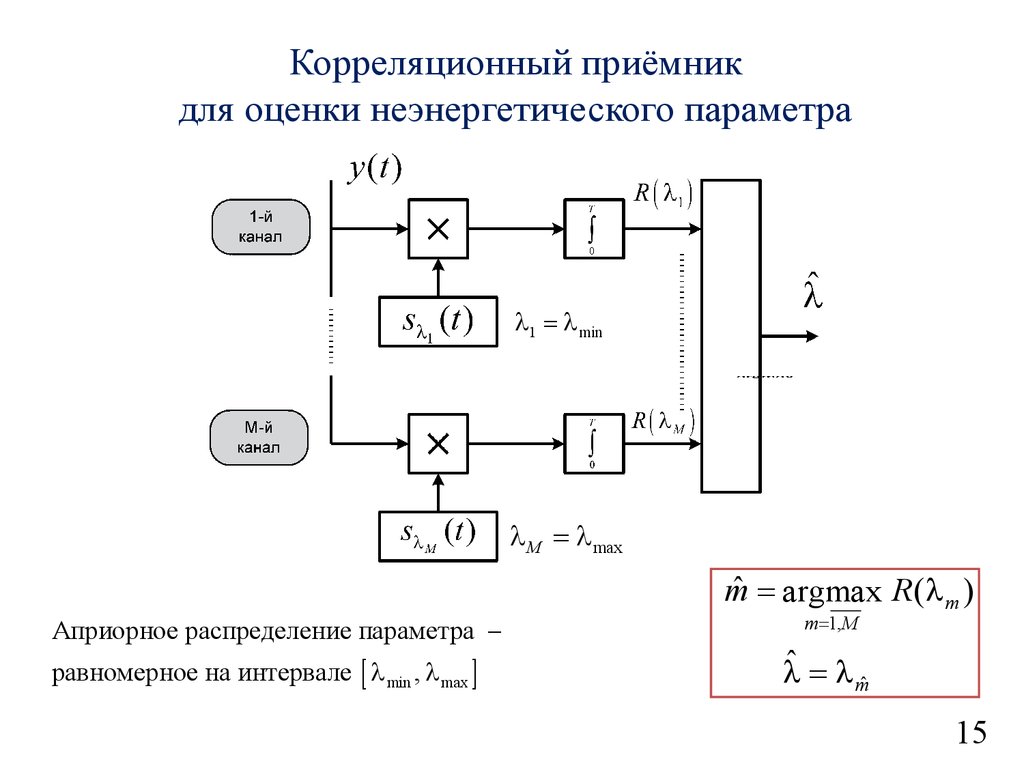
16.
Корреляционный приёмникдля оценки неэнергетического параметра
1 = min
M = max
Априорное распределение параметра
равномерное на интервале [ min , max ]
mˆ = argmax R ( m )
m=1,M
ˆ = mˆ
15













 Физика
Физика








