Сложное движение материальной точки

1.

Сложное движение материальной точки
Движение материальной точки называется сложным, если
точка движется относительно некоторой системы координат,
которая в свою очередь движется относительно другой
системы координат, принимаемой за неподвижную.

2.

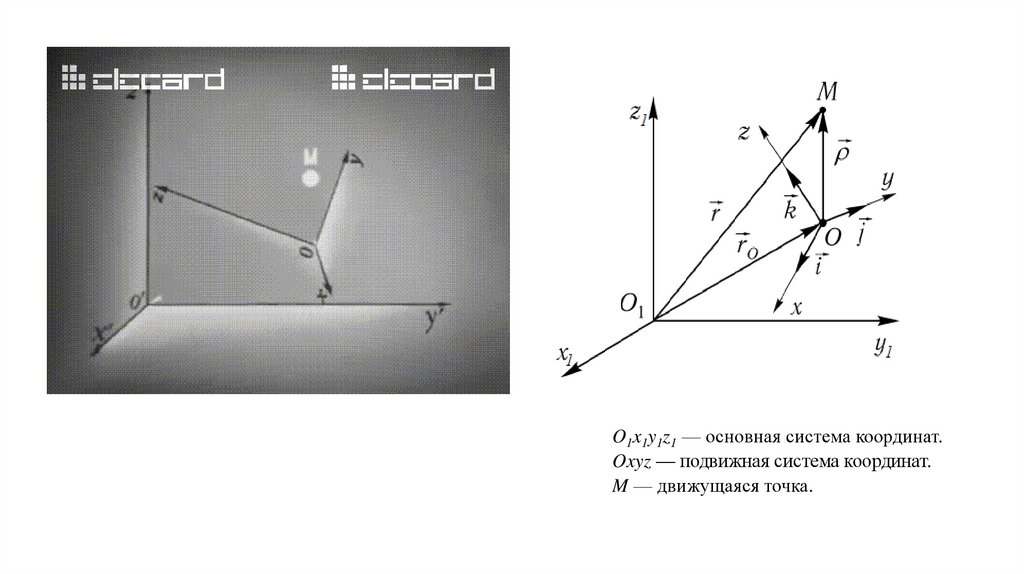
O1x1y1z1 — основная система координат.
Oxyz — подвижная система координат.
M — движущаяся точка.

3.

Рассмотрим основную систему отсчета
О1x1y1z1, положение точки в данной системе
отсчета задается функцией от времени
радиус-вектора r r (t )
O1x1y1z1 — основная система координат.
Oxyz — подвижная система координат.
M — движущаяся точка.
Также введем подвижную систему отсчета
Оxyz, начало которой задается с помощью
радиус-вектора точки О. Положение точки в
подвижной
системе
отсчета
называется
относительным и записывается через функцию
радиус-вектора ρ, куда входят постоянные орты
подвижных осей и функции времени, задающие
координаты точки в подвижной системе
координат
x(t ) i y (t ) j z (t ) k
Переносное движение задается радиус-вектором точки О (начало подвижной
системы отсчета) и положением единичных ортов подвижной системы в
различные моменты времени
r r (t ), i i (t ), j j (t ), k k (t )
O
O

4.

Положение точки М относительно неподвижной
системы
отсчета
O1x1y1z1,
может
быть
определено радиусом-вектором
r rO rO xi y j z k
Движение точки M по отношению к
основной системе координат называется
абсолютным движением.
Движение точки M по отношению к
подвижной системе координат называется
относительным движением.
Переносное движение — движение
подвижной системы координат по отношению к
основной.

5.

Абсолютная скорость и абсолютное ускорение точки
— это скорость и ускорение точки в основной системе
координат:
2
dr dV d r
V ; a
2
dt
dt dt
Скорость и ускорение точки относительно подвижной системы координат
называют относительными (relative):
xi y j z k
Vr
d
dt i , j
xi y j z k
,k const
ar
dV
dt
xi y j z k
i , j ,k const

6.

Переносной скоростью (переносным ускорение)
точки называют скорость (ускорение) того места
подвижной системы координат по отношению к
неподвижной, с которой в данный момент совпадает
рассматриваемая точка.
Ve
dr
d
r
dt x,y,z const dt
O
ae
dVe
dt
xi y j z k rO x i y j z k
rO x i y j z k
x,y,z const

7.

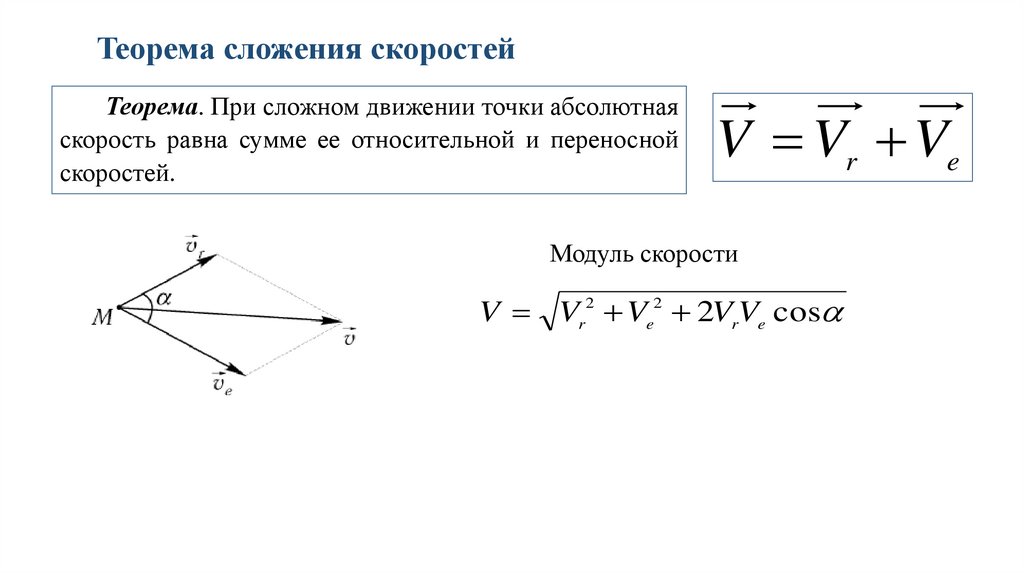
Teopeмa сложения скоростей
Теорема. При сложном движении точки абсолютная
скорость равна сумме ее относительной и переносной
скоростей.
V Vr Ve
Модуль скорости
V Vr2 Ve2 2VrVe cos

8.

Теорема о сложении ускорений (теорема Кориолиса)
Теорема. При непоступательном переносном движении абсолютное
ускорение точки находится как сумма трех ускорений: относительного,
переносного и ускорения Кориолиса.
a ar ae ac
ac 2 e Vr
- ускорение Кориолиса
угловая скорость переносного вращения
e

9.

Ускорение Кориолиса учитывает изменение относительной скорости,
вызванное переносным движением, и изменение переносной скорости,
вызванное относительным движением.
ac 2 e Vr
Рассмотрим эффект Кориолиса, который проявляется при движении платформы, на
которой сидят 2 человека.
Если платформа неподвижна, они спокойно кидают друг другу мяч, достигая целей.
Когда платформа начинает вращаться, траектория меняется. Рассмотрим эту
траекторию в подвижной системе координат.
Если в неподвижной системе координат траектория была прямой линией, если
смотреть сверху, то в данном случае траектория криволинейна.
При этом траектория зависит от того, в каком направлении платформа вращается.
Вот так отражаются рассмотренные нами законы на движении мяча.
Правило Жуковского для определения
направления ускорения Кориолиса надо вектор относительной скорости
спроецировать на плоскость,
перпендикулярную оси вращения, и
повернуть в сторону вращения на угол
90 .

10.

Абсолютная скорость будет равна скорости движения эскалатора плюс
скорость движения человека
Человек идет в противоположном
направлении движения эскалатора
V Vэскалатора Vчеловека
Человек идет в направлении
движения эскалатора
V Vэскалатора Vчеловека

11.

Рассмотрим модуль вооружения. В данном
случае переносное движение связано с
вращением башни модуля, а относительное
движение связано с движением вертикальной
плоскости ствола.
Свяжем неподвижную систему отсчета
О1x'y'z' с корпусом, подвижную систему отсчета
свяжем со стволом, и в данном случае
относительная скорость будет направлена вдоль
оси z, переносная скорость будет направлена
вдоль оси y.
Эти
две
скорости
будут
взаимно
перпендикулярны,
скорость
точки
ствола
находится по указанной формуле

12.

Мостовой кран перемещается вдоль цеха. По
крану движется тележка.
Относительное движение – это движение
точки по перемещающемуся телу. В данном
примере относительное движение – движение
тележки по крану.
Переносное
движение
–
движение
крана вдоль цеха.
Абсолютное движение – это движение
точки относительно стойки (неподвижной
системы отсчета). В рассматриваемом примере
абсолютное движение – движение тележки
относительно цеха.

13.

Вдоль цеха по рельсам с постоянной скоростью 0,1 м/с перемещается мостовой кран, по
которому с постоянной скоростью 0,2 м/с движется тележка. Определить абсолютную скорость
тележки.
Проводим через точку М линии скоростей. Траектория
Вид сверху:
относительного движения точки М – прямая АВ; переносным
движением является поступательное движение крана вдоль
стороны ОЕ цеха; траекторию абсолютного движения
точки М установить по условию задачи нельзя,
поэтому линию а–а проводим под некоторым углом
к
линии е–е, считая искомой величиной.
Построим параллелограмм скоростей: по условию задачи
известны направления относительной скорости точки (она
равна скорости движения тележки по крану) и переносной
скорости (она равна скорости точки крана, с которой в
данный момент совпадает тележка); откладываем от
точки М по линии r–r вектор относительной скорости, а по
линии е–е – вектор переносной скорости; затем достраиваем
параллелограмм скоростей.
V Vr2 Ve2 0,22 0,12 0,224 м / с tg
Vr 0,2
2
Ve 0,1