Похожие презентации:
Сложное движение точки. Тема 4
1.
2.
Движениематериальной
точки
по
отношению к двум системам отсчета
одновременно, одна из которых является
условно
неподвижной,
а
другая
движется по отношению к первой
называется сложным или составным
2
3.
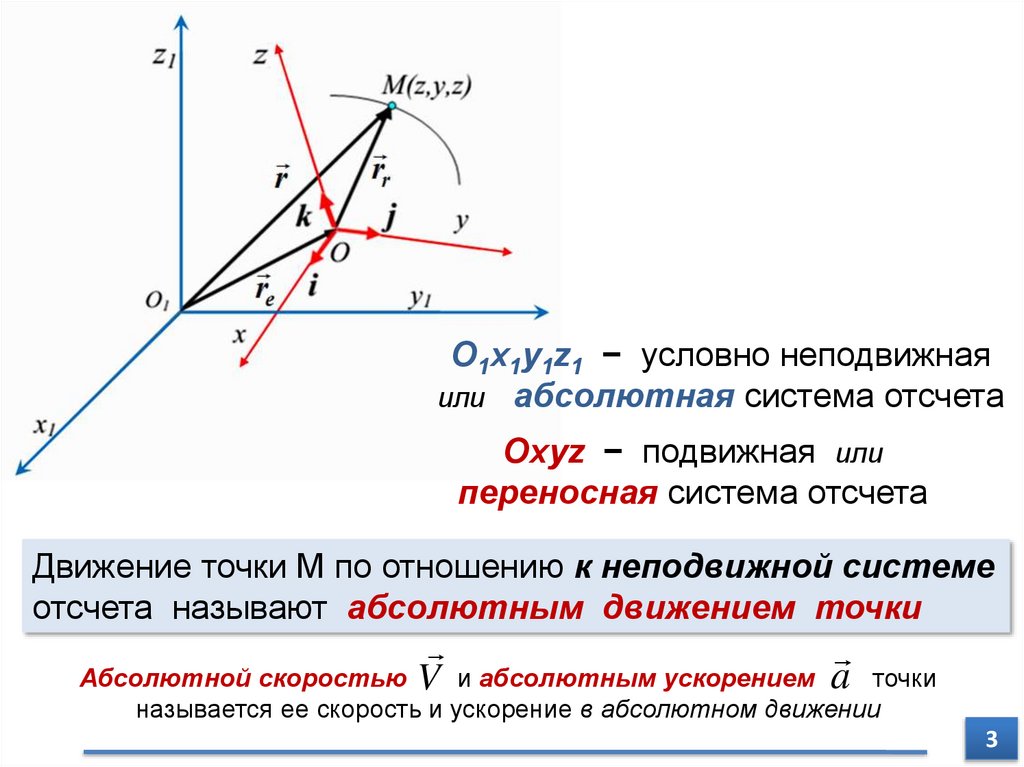
О1x1y1z1 − условно неподвижнаяили абсолютная система отсчета
Оxyz − подвижная или
переносная система отсчета
Движение точки М по отношению к неподвижной системе
отсчета называют абсолютным движением точки
Абсолютной скоростью V и абсолютным ускорением a точки
называется ее скорость и ускорение в абсолютном движении
3
4.
Относительным называется движение точки Мотносительно подвижной системы отсчета Oxyz
Траектория, описываемая точкой М в относительном
движении, называется относительной траекторией.
Все кинематические характеристики относительного
движения обозначаются индексом«r»
Скорость движения точки М по отношению к подвижной
системе отсчета
Oxyz называется относительной
скоростью V
r
Ускорение движения точки М по отношению к подвижной
системе отсчета
Oxyz называется относительным
ускорением ar
4
5.
Движение, совершаемое подвижной системой отсчетаOxyz и всеми неизменно связанными с ней точками
пространства относительно неподвижной системы
O1x1y1z1, называется переносным движением
Траектория, описываемая точкой в переносном
движении, называется переносной траекторией.
Все кинематические характеристики переносного
движения обозначаются индексом «e»
Скорость той неизменно связанной с подвижной
системой отсчета Oxyz точки, с которой в данный момент
совпадает
точка М, называется переносной скоростью
точки V
e
Ускорение этой
точки называется переносным
ускорением ae
5
6.
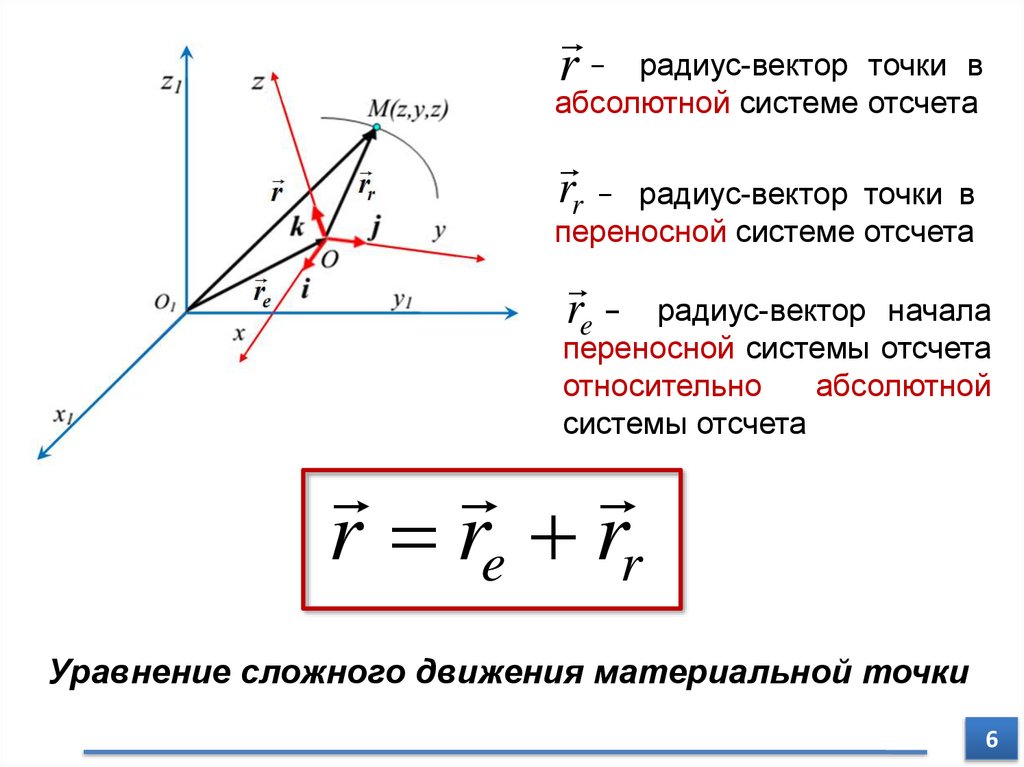
r − радиус-вектор точки вабсолютной системе отсчета
rr − радиус-вектор точки в
переносной системе отсчета
re −
радиус-вектор начала
переносной системы отсчета
относительно
абсолютной
системы отсчета
r re rr
Уравнение сложного движения материальной точки
6
7.
drАбсолютная скорость точки равна: V
dt
Так как r re rr или r rÎ rr , где
rr xi yj zk
i , j ,k – орты подвижных осей
Орты переносной системы отсчета перемещаются вместе
с подвижными осями и их направление меняется со
временим, следовательно это переменные величины
i i ( t ), j j ( t ), k k ( t )
7
8.
Тогда абсолютная скорость точки определяется как:dr O d
V
( xi yj zk )
dt dt
drO dx dy dz
di
dj
dk
i
j k x y z
dt dt
dt
dt
dt
dt
dt
где
dx dy dz
i
j k Vr – относительная скорость точки
dt
dt
dt
drO
di
dj
dk
x y z
Ve – переносная скорость точки
dt
dt
dt
dt
8
9.
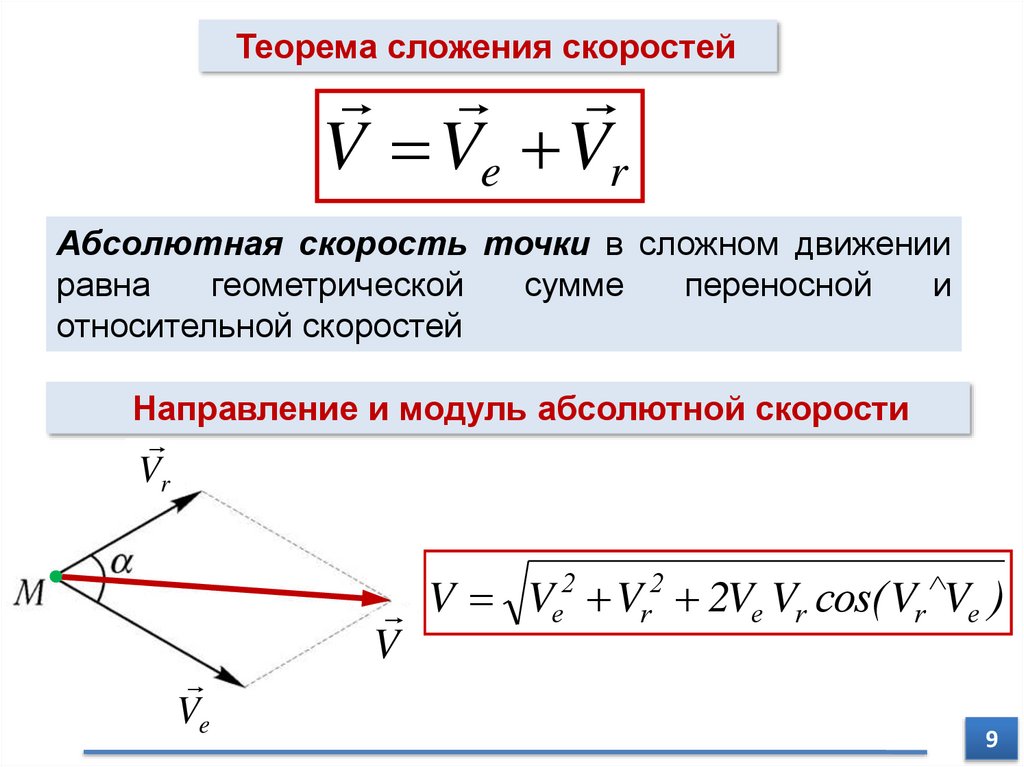
Теорема сложения скоростейV Ve Vr
Абсолютная скорость точки в сложном движении
равна
геометрической
сумме
переносной
и
относительной скоростей
Направление и модуль абсолютной скорости
Vr
Ve
V
V
2
2
Ve Vr 2Ve Vr cos( Vr Ve )
9
10.
.Поступательное переносное движение
dV
Абсолютное ускорение точки равно: a
dt
2
2
2
d r d rO d
a 2 2 2 ( xi yj zk )
dt
dt
dt
Так как подвижные оси при таком движении не поворачиваются, то
направление их орт со временим не меняется,
следовательно
i const , j const , k const
Теорема сложения ускорений
a ae a r
При поступательном переносном движении абсолютное
ускорение точки равно геометрической сумме переносного и
относительного ускорений
10
11.
Непоступательное переносное движение.
Абсолютное ускорение точки равно:
2
d
a
dt
где
2
r d rO d 2
2 2 ( xi yj zk ),
2
dt
dt
i i ( t ), j j ( t ), k k ( t ),
так как переносная система отсчета вращается.
Тогда
2
2
2
2
dx di dy dj dz dk
dV d rO d x
d y
d z
a
2 2 i 2 j 2 k 2
dt
dt
dt
dt
dt
dt dt dt dt dt dt
2
2
2
d i
d j
d k
x 2 y 2 z 2
dt
dt
dt
11
12.
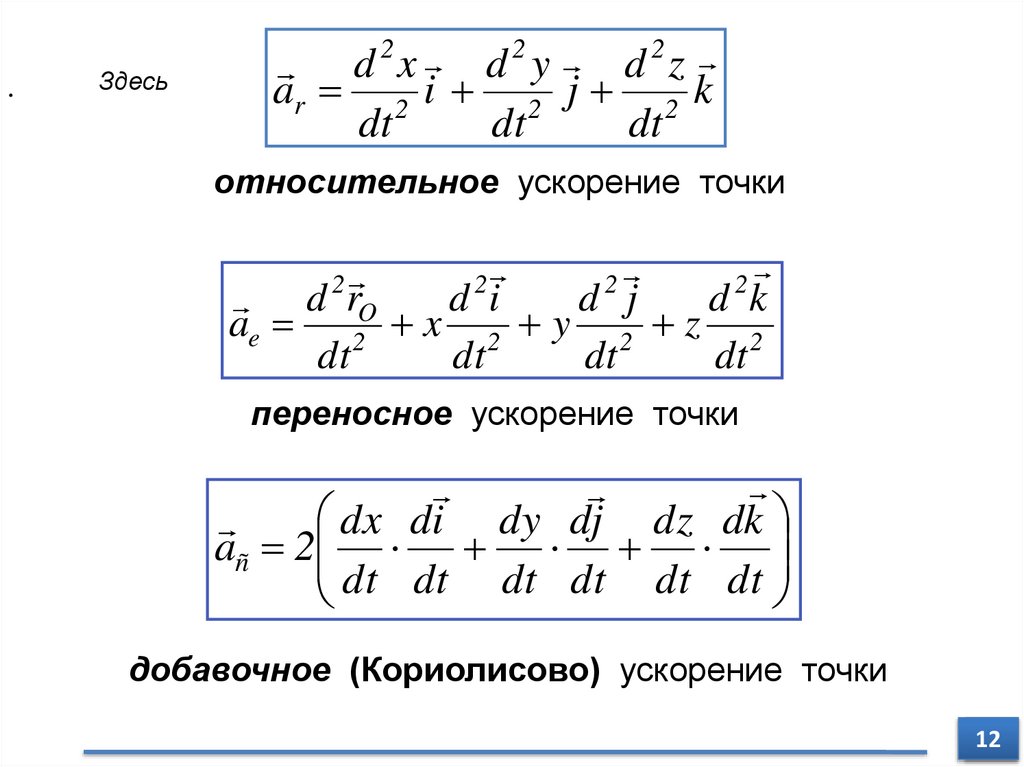
.Здесь
d 2x d 2 y d 2z
ar 2 i 2 j 2 k
dt
dt
dt
относительное ускорение точки
2
d 2i
d2 j
d 2k
d rO
ae 2 x 2 y 2 z 2
dt
dt
dt
dt
переносное ускорение точки
dx di dy dj dz dk
añ 2
dt dt dt dt dt dt
добавочное (Кориолисово) ускорение точки
12
11
13.
.Теорема сложения ускорений
(Теорема Кориолиса)
a aå ar ac
При
непоступательном
переносном
движении абсолютное ускорение точки
равно геометрической сумме переносного,
относительного и кориолисова ускорений
13
12
14.
Кориолисовым ускорением (ускорением Кориолиса)называется составляющая абсолютного ускорения точки
в сложном движении, равная удвоенному векторному
произведению угловой скорости переносного вращения
на относительную скорость точки
ac 2 eVr
14
13
15.
Модуль кориолисова ускорения.
ac 2 eVr sin( e Vr )
Ускорение Кориолиса равняется нулю в трех случаях:
1. если e 0 т. е. в случае поступательного переносного движения
или в моменты обращения в нуль угловой скорости непоступательного
переносного движения;
2. если Vr 0 , т. е. в случае относительного покоя точки или в
моменты обращения в нуль относительной скорости движущейся точки;
3. если sin( e Vr ) 0 , т.е. в случае, когда ( e Vr ) 0 или ( e Vr )
т.е. относительная скорость точки параллельна оси переносного
вращения.
15
14
16.
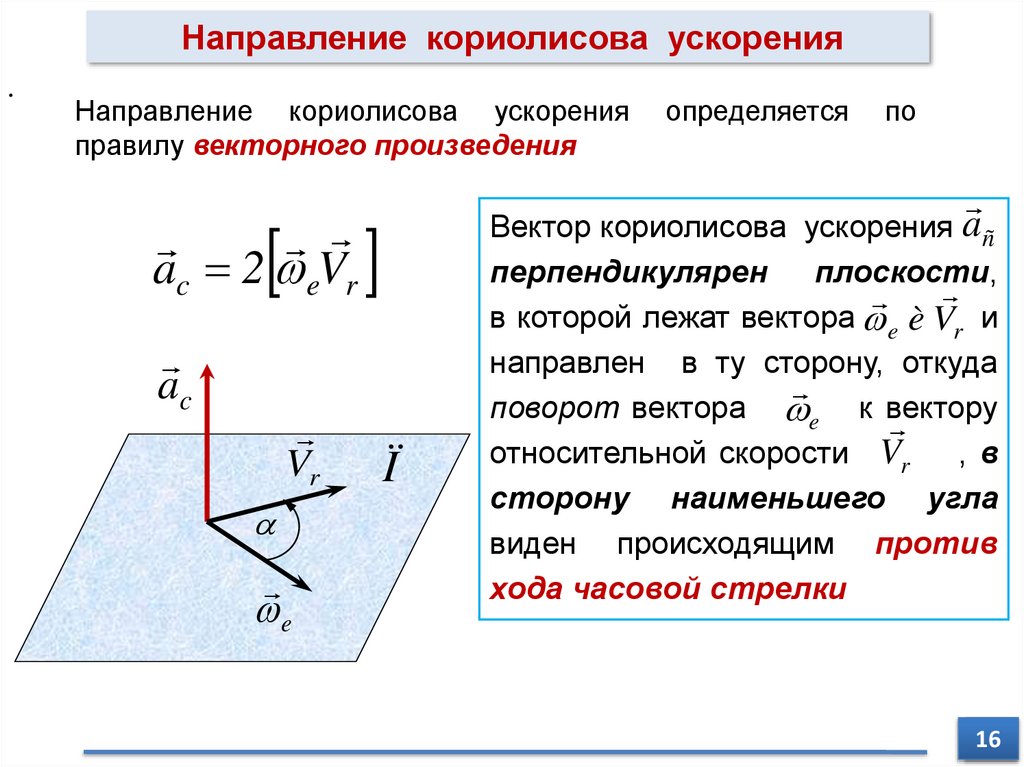
Направление кориолисова ускорения.
Направление кориолисова ускорения
правилу векторного произведения
ac 2 eVr
ac
Vr
e
определяется
по
Вектор кориолисова ускорения añ
Ï
перпендикулярен плоскости,
в которой лежат вектора e è Vr и
направлен в ту сторону, откуда
поворот вектора e к вектору
относительной скорости Vr
,в
сторону наименьшего угла
виден происходящим против
хода часовой стрелки
16
15
17.
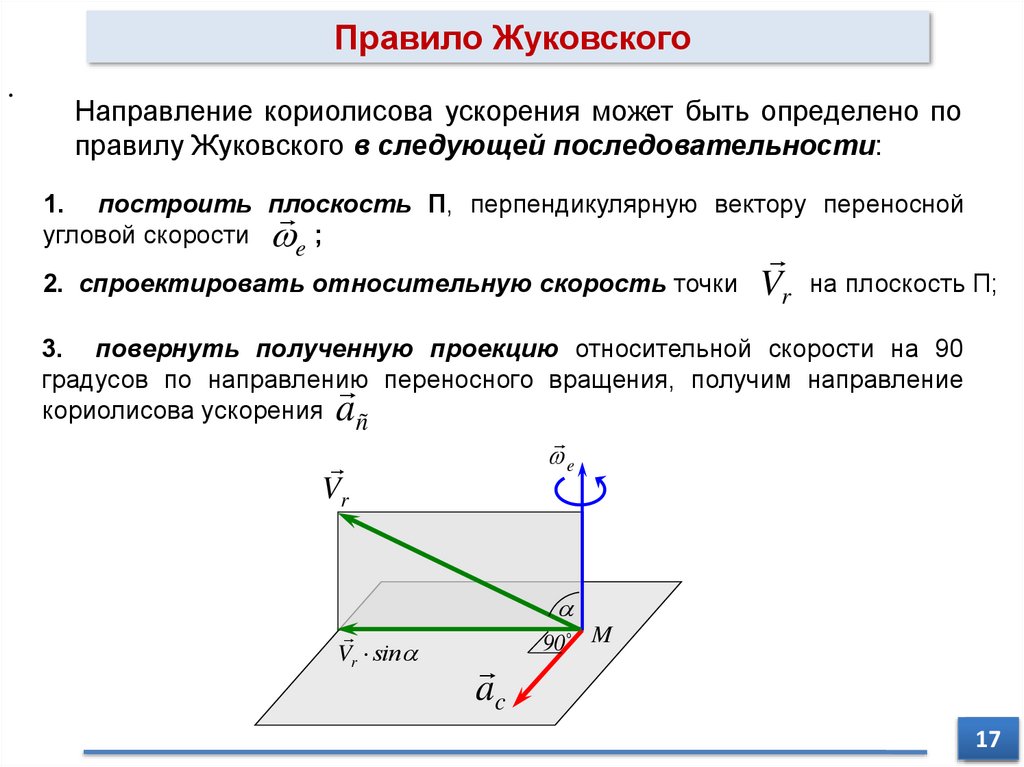
Правило Жуковского.
Направление кориолисова ускорения может быть определено по
правилу Жуковского в следующей последовательности:
1. построить плоскость
Π, перпендикулярную вектору переносной
угловой скорости e ;
2. спроектировать относительную скорость точки Vr на плоскость Π;
3. повернуть полученную проекцию относительной скорости на 90
градусов по направлению
переносного вращения, получим направление
кориолисова ускорения añ
e
Vr
Vr sin
ac
90 M
17
16
18.
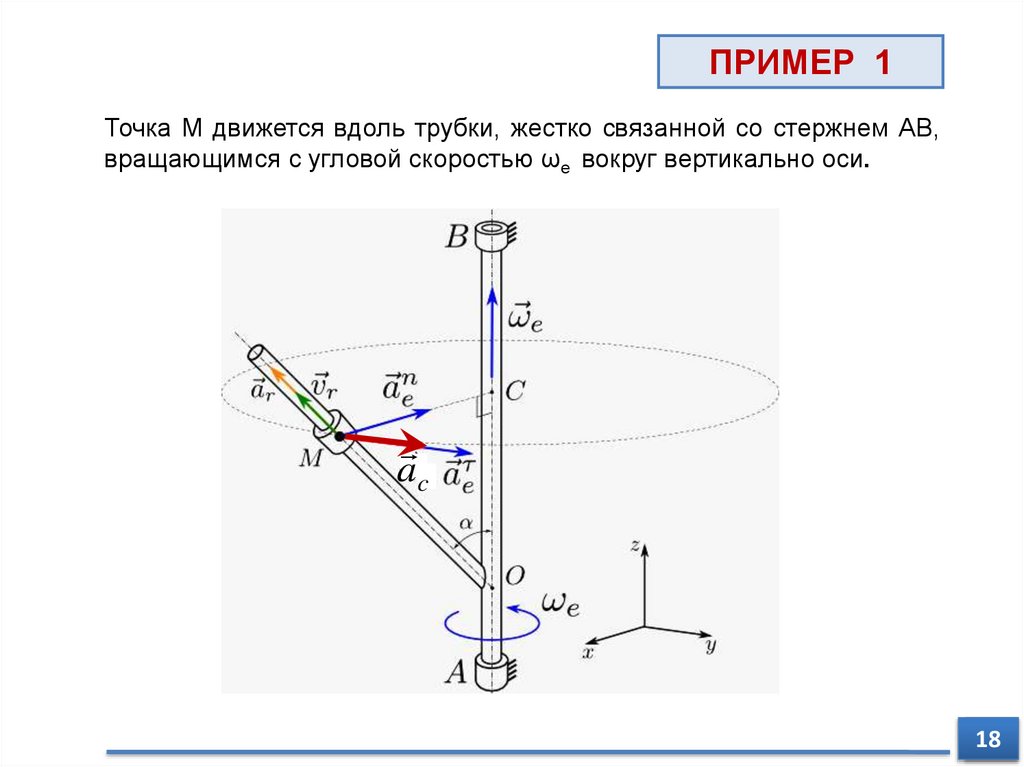
ПРИМЕР 1Точка М движется вдоль трубки, жестко связанной со стержнем АВ,
вращающимся с угловой скоростью ωe вокруг вертикально оси.
ac
18
17
19.
ПРИМЕР 2О
2
1
В
А
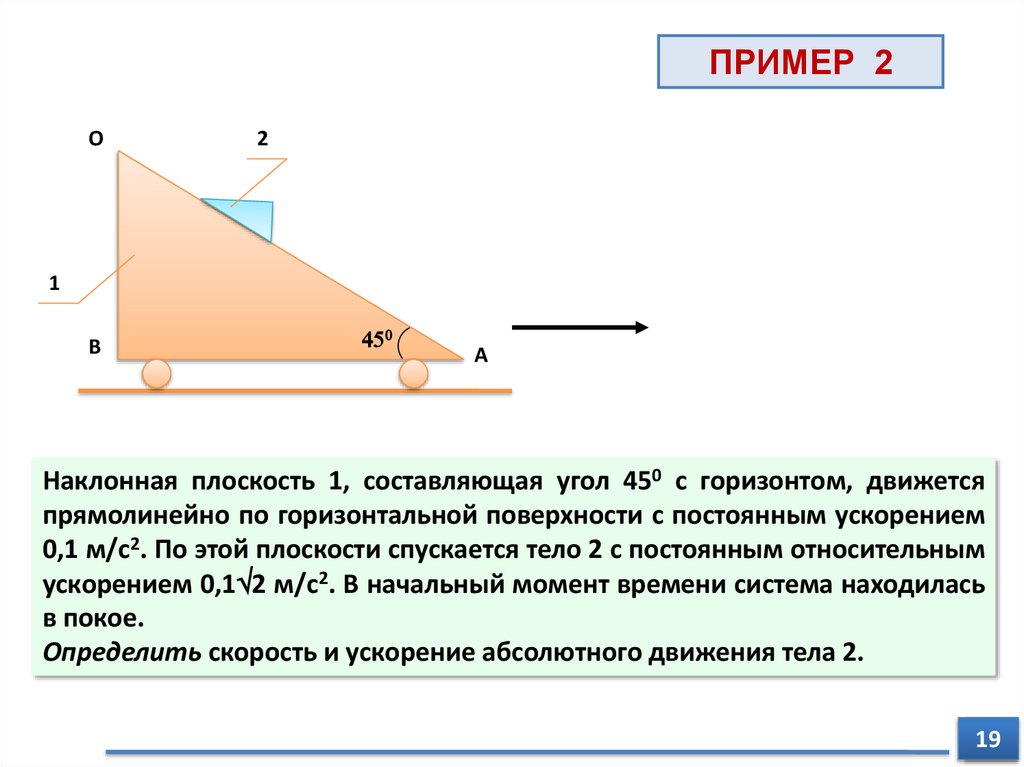
Наклонная плоскость 1, составляющая угол 450 с горизонтом, движется
прямолинейно по горизонтальной поверхности с постоянным ускорением
0,1 м/с2. По этой плоскости спускается тело 2 с постоянным относительным
ускорением 0,1 2 м/с2. В начальный момент времени система находилась
в покое.
Определить скорость и ускорение абсолютного движения тела 2.
19
1
20.
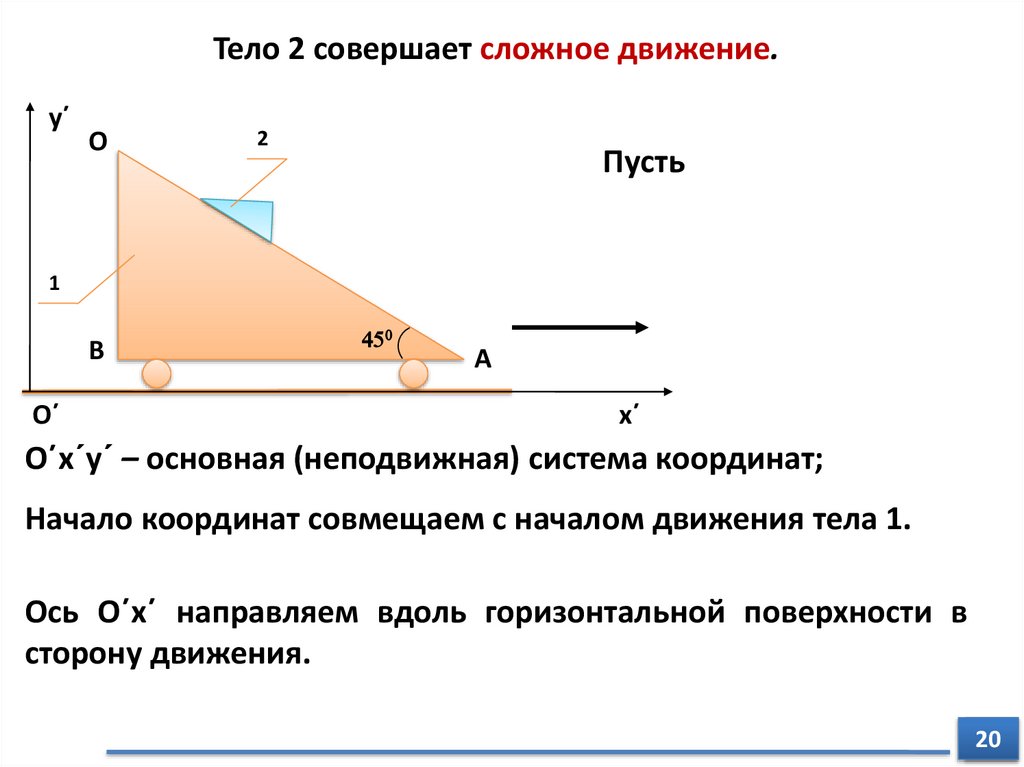
Тело 2 совершает сложное движение.y΄
О
2
Пусть
1
В
О΄
А
x΄
О΄x΄y΄ – основная (неподвижная) система координат;
Начало координат совмещаем с началом движения тела 1.
Ось О΄x΄ направляем вдоль горизонтальной поверхности в
сторону движения.
20
1
21.
yy΄
О
2
1
В
О΄
А
x
x΄
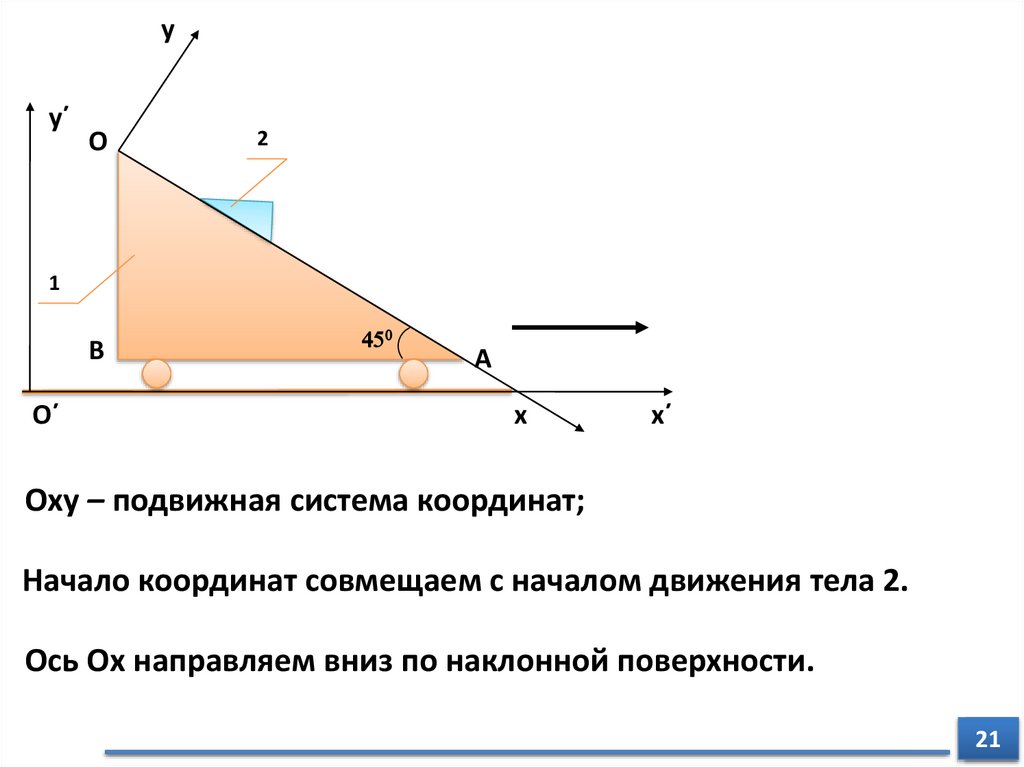
Оxy – подвижная система координат;
Начало координат совмещаем с началом движения тела 2.
Ось Оx направляем вниз по наклонной поверхности.
21
1
22.
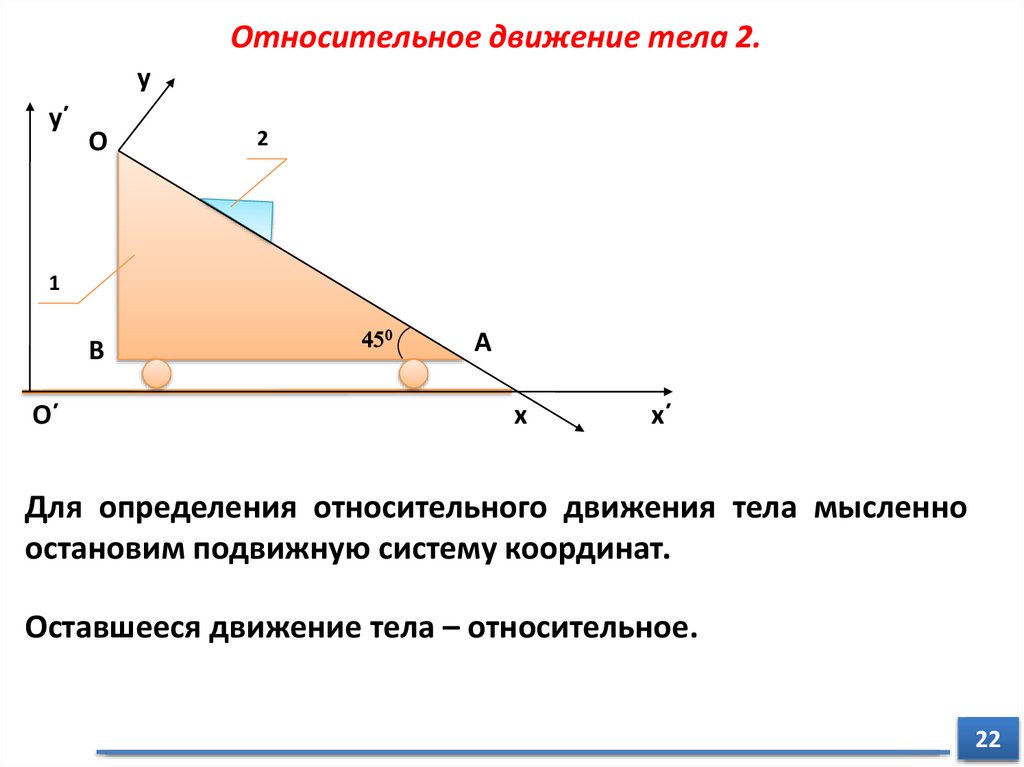
Относительное движение тела 2.y
y΄
О
2
1
В
О΄
А
x
x΄
Для определения относительного движения тела мысленно
остановим подвижную систему координат.
Оставшееся движение тела – относительное.
22
1
23.
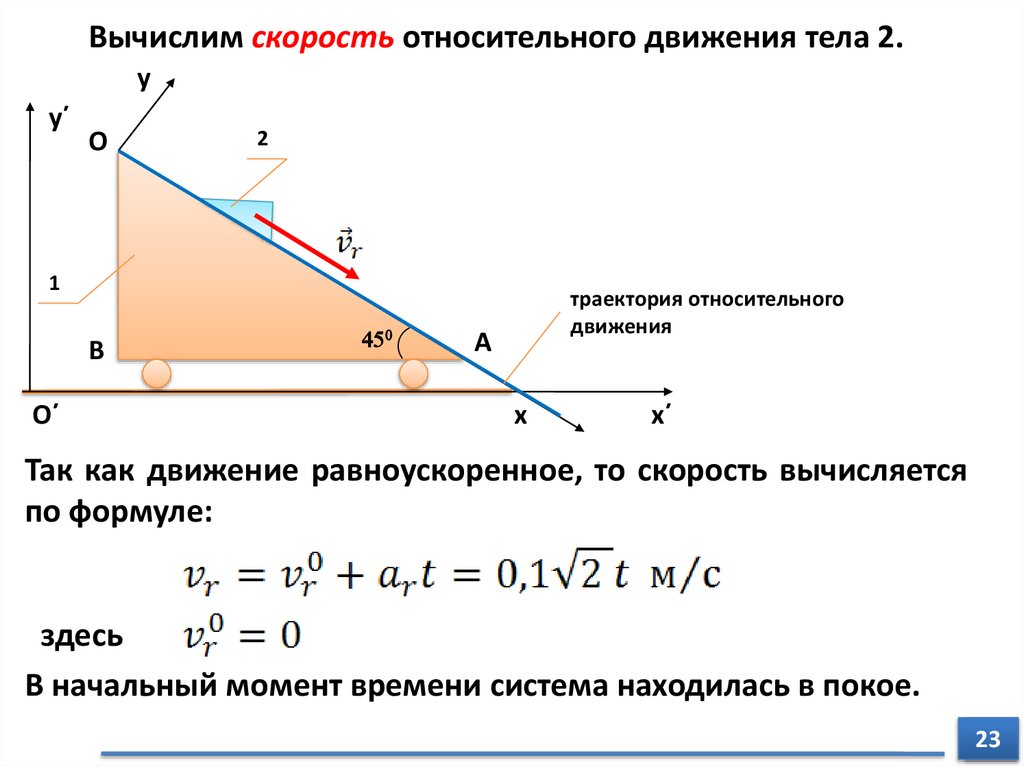
Вычислим скорость относительного движения тела 2.y
y΄
О
2
1
В
О΄
траектория относительного
движения
А
x
x΄
Так как движение равноускоренное, то скорость вычисляется
по формуле:
здесь
В начальный момент времени система находилась в покое.
23
1
24.
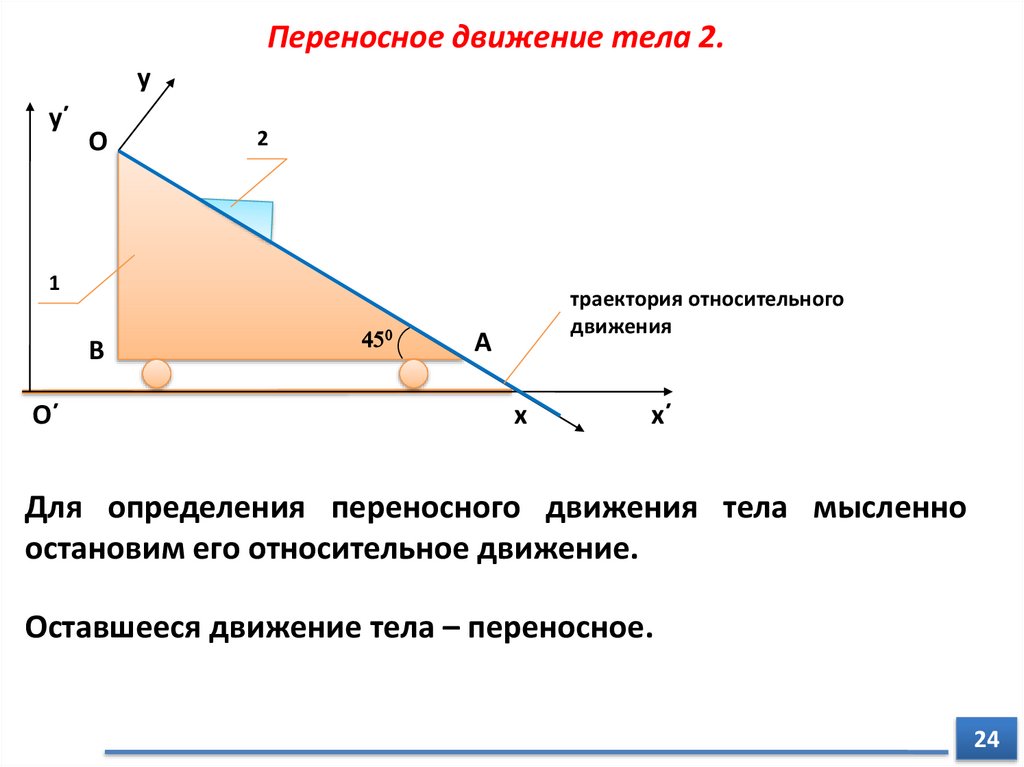
Переносное движение тела 2.y
y΄
О
2
1
В
О΄
траектория относительного
движения
А
x
x΄
Для определения переносного движения тела мысленно
остановим его относительное движение.
Оставшееся движение тела – переносное.
24
25.
yy΄
О
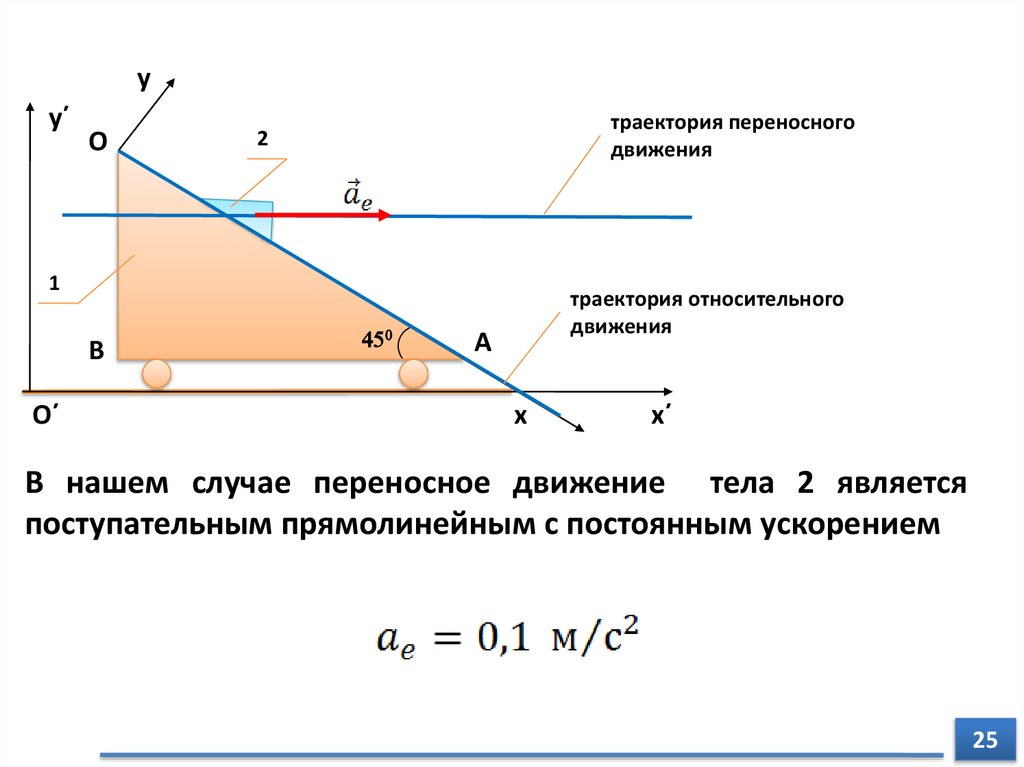
траектория переносного
движения
2
1
В
О΄
траектория относительного
движения
А
x
x΄
В нашем случае переносное движение тела 2 является
поступательным прямолинейным с постоянным ускорением
25
26.
Вычислим скорость переносного движения тела 2.y
y΄
О
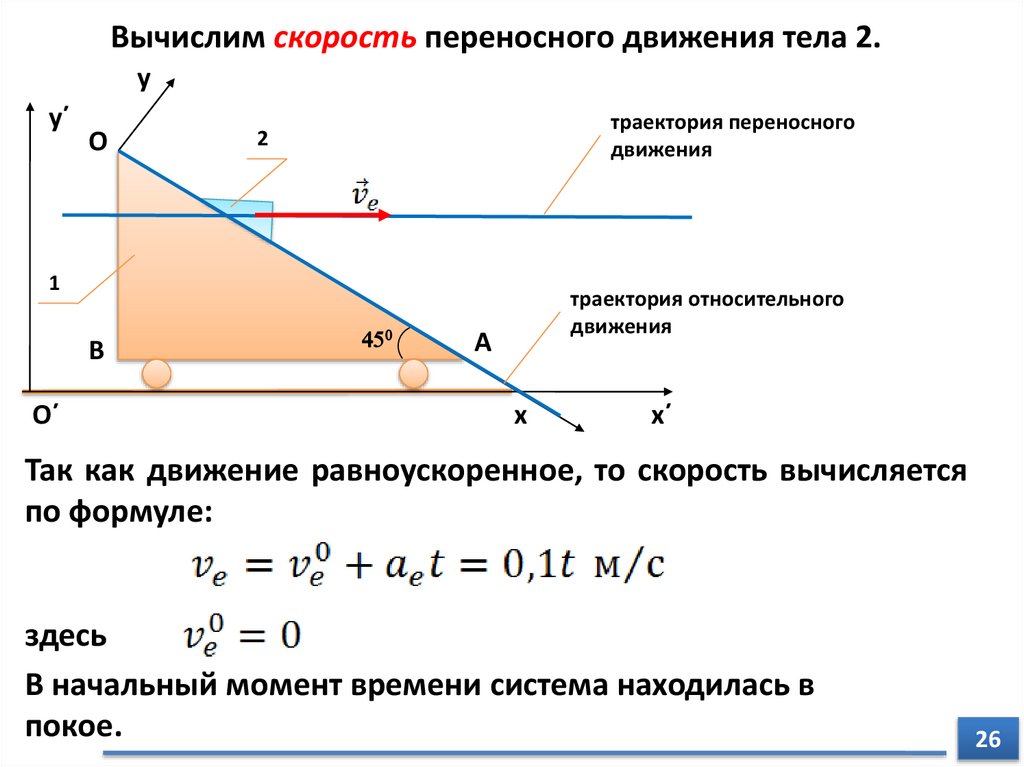
траектория переносного
движения
2
1
В
О΄
траектория относительного
движения
А
x
x΄
Так как движение равноускоренное, то скорость вычисляется
по формуле:
здесь
В начальный момент времени система находилась в
покое.
26
27.
Вычислим скорость абсолютного движения тела 2.y
y΄
О
2
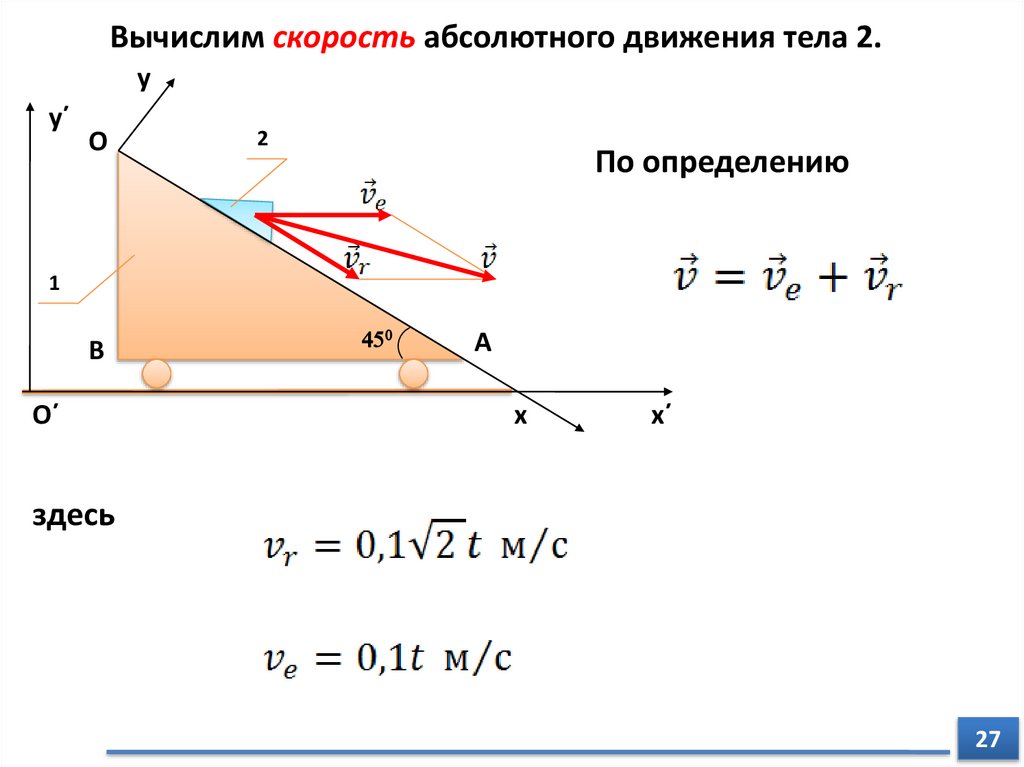
По определению
1
В
О΄
А
x
x΄
здесь
27
28.
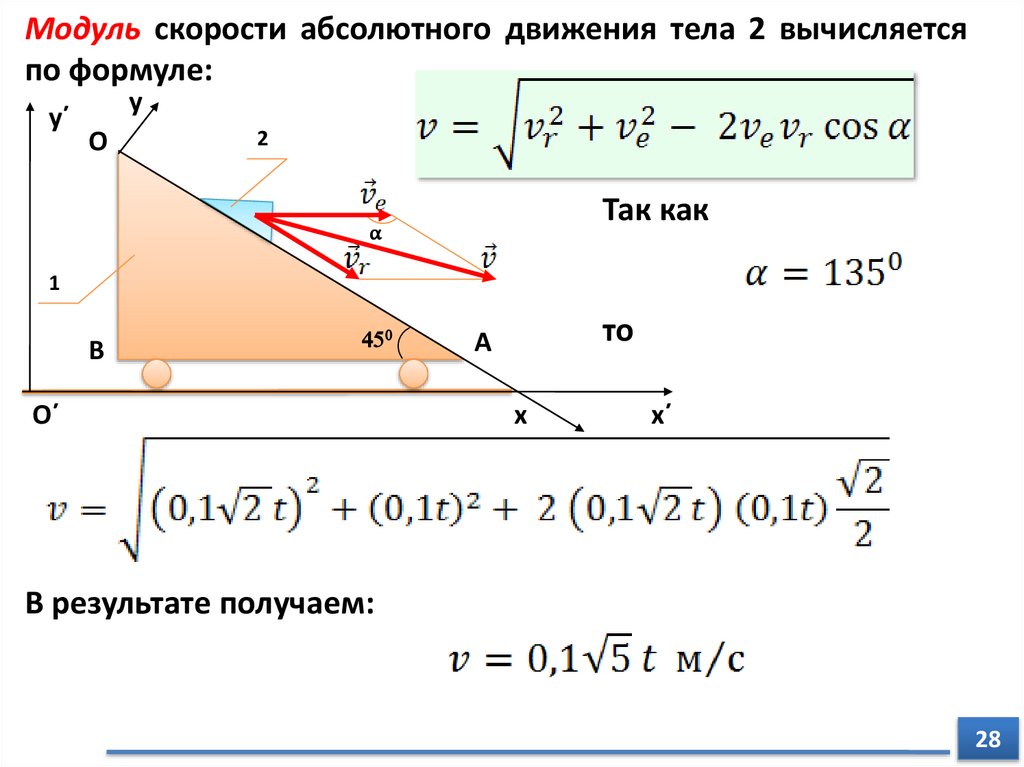
Модуль скорости абсолютного движения тела 2 вычисляетсяпо формуле:
y΄
y
О
2
Так как
α
1
В
О΄
то
А
x
x΄
В результате получаем:
28
29.
Вычислим ускорение абсолютного движения тела 2.y
y΄
О
По определению
2
1
В
О΄
А
x
x΄
здесь
Так как переносное движение является поступательным.
29
30.
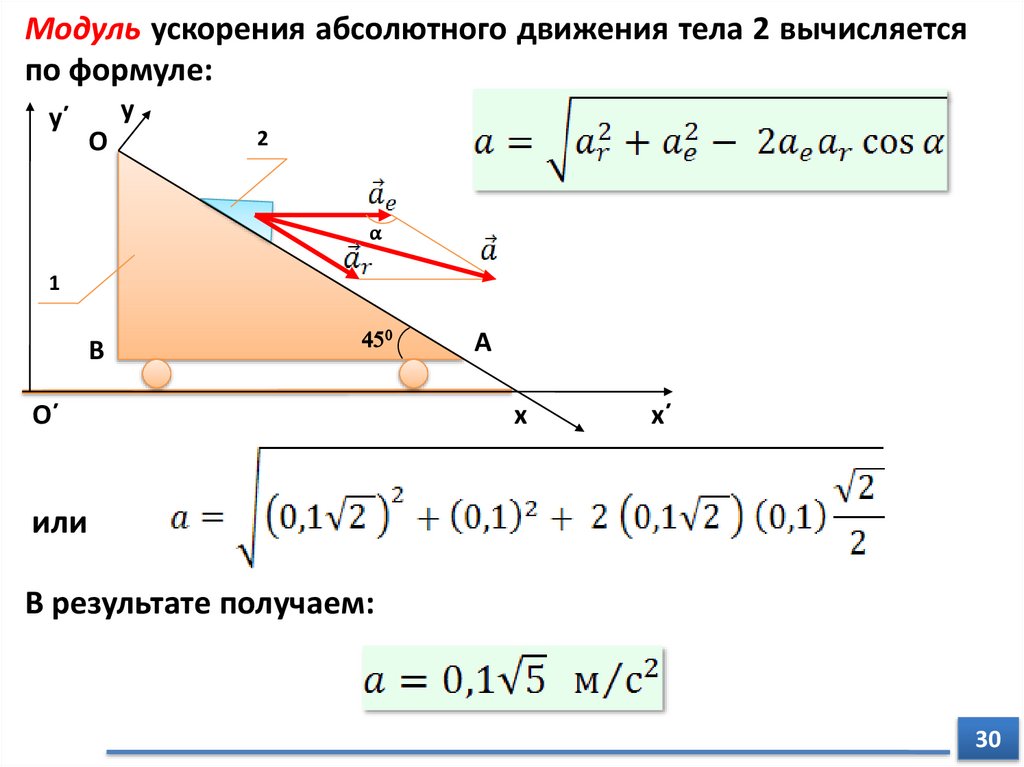
Модуль ускорения абсолютного движения тела 2 вычисляетсяпо формуле:
y΄
y
О
2
α
1
В
О΄
А
x
x΄
или
В результате получаем:
30
31.
ЛИТЕРАТУРА1. Яблонский А.А., Никифорова В.М. Курс теоретической
механики – М.: Интеграл-Пресс, 2007. – 608 с.
2. Тарг С.М. Краткий курс теоретической механики. – М.:
Высшая школа, 1986. – 416 с.
3. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической
механики. СПб.: Лань. 2009. – 736 с.
4. Бухгольц Н.Н. Основной курс теоретической механики. В
2-х ч. Ч. 1. Кинематика, статика, динамика материальной
точки. СПб.: Лань, 2009. – 480 с.
5. Диевский В.А. Теоретическая механика – СПб.: Лань,
2005. – 320 с.













 Физика
Физика








