Теория комплексных чисел. Геометрическая интерпретация комплексного числа. (Тема 3)

1. Теория комплексных чисел

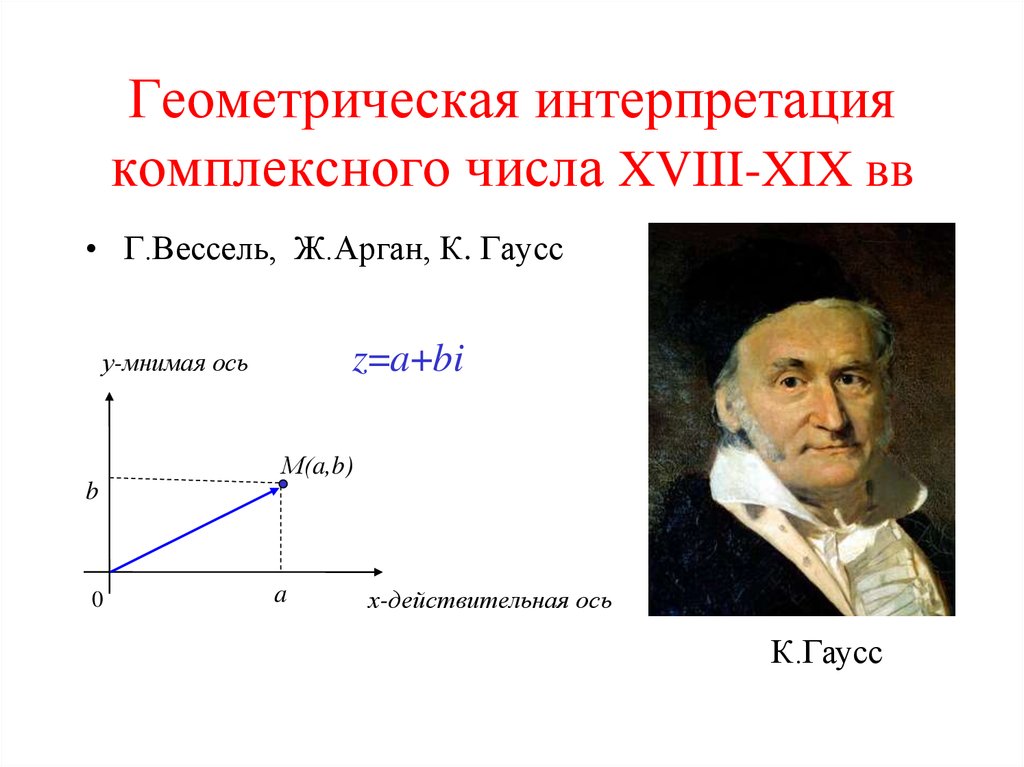
2. Геометрическая интерпретация комплексного числа XVIII-XIX вв

• Г.Вессель, Ж.Арган, К. Гаусс
z=a+bi
у-мнимая ось
М(a,b)
b
0
a
х-действительная ось
К.Гаусс

3. 1. Изобразить на комплексной плоскости следующие числа:

у
z1 3 2 i
2
z5
0
z 2 z1
z 3 z1
z 4 Re z1
z 5 Im z1
-3
3
х
z4
-2

4. Модуль комплексного числа

• Модулем комплексного числа
z=a+bi
называется длина вектора z
:
у-мнимая ось
М(a,b)
b
z a 2 b2
r z
0
a
х-действительная ось

5. 2. Найти модуль комплексного числа:

z a 2 b2
z1 2 i
z 2 2 6 5i
z1 2 2 1 4 1 5
2
z2
2 6
2
5 2 24 25 49 7
z3 i
z3 0 2 12 1 1
z 4 4
z4
4 2 0 2
16 4

6. Аргумент комплексного числа

• Аргументом комплексного числа называется угол ,
который образует вектор OM с положительным
направлением оси абсцисс.
=arg z
у-мнимая ось
М(a,b)
b
z
0
х-действительная ось
a

7. Аргумент определяется неоднозначно

z 1 i
у
у
у
1
1
1
2
1
0
1
1
4
х
0
1
х
9
2 2
4
4
3
0
3
1
4
х
2
7
4
Любые два аргумента комплексного числа отличаются друг
от друга слагаемым, кратным 2π.
Для нашего примера: k 2 k , k Z
4

8. 3. Найти аргументы комплексного числа:

z2 1
z1 i
у
arg z1
0
3
2 k , k Z
2
arg z2 0 2 k , k Z
у
х
0
1
х
-1
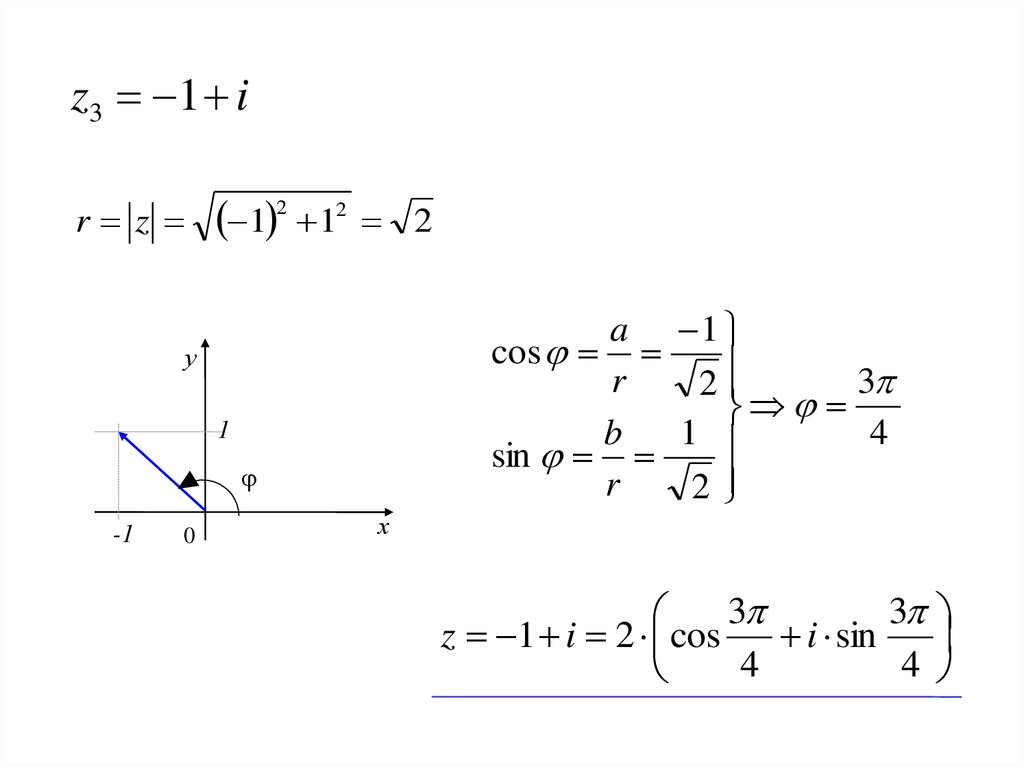
z3 1 3 i
tan
3
1
у
-1
0
3
х
3
3
3
4
3
arg z3
4
2 k , k Z
3

9. 4.Найти модуль и аргумент комплексного числа:

3 i17
z
18
i
z
tan
3
2
b
a
3 i
3 i
1
12 3 1 4 2
1
3
5
6
6
у
1
6
3
0
х
5
arg z
2 k , k Z
6

10. Тригонометрическая форма комплексного числа

2
2
r z a b
z a bi
у
М(a,b)
b
z
a
cos
r a r cos
b b r sin
sin
r
0
a
х
z a bi r (cos i sin )

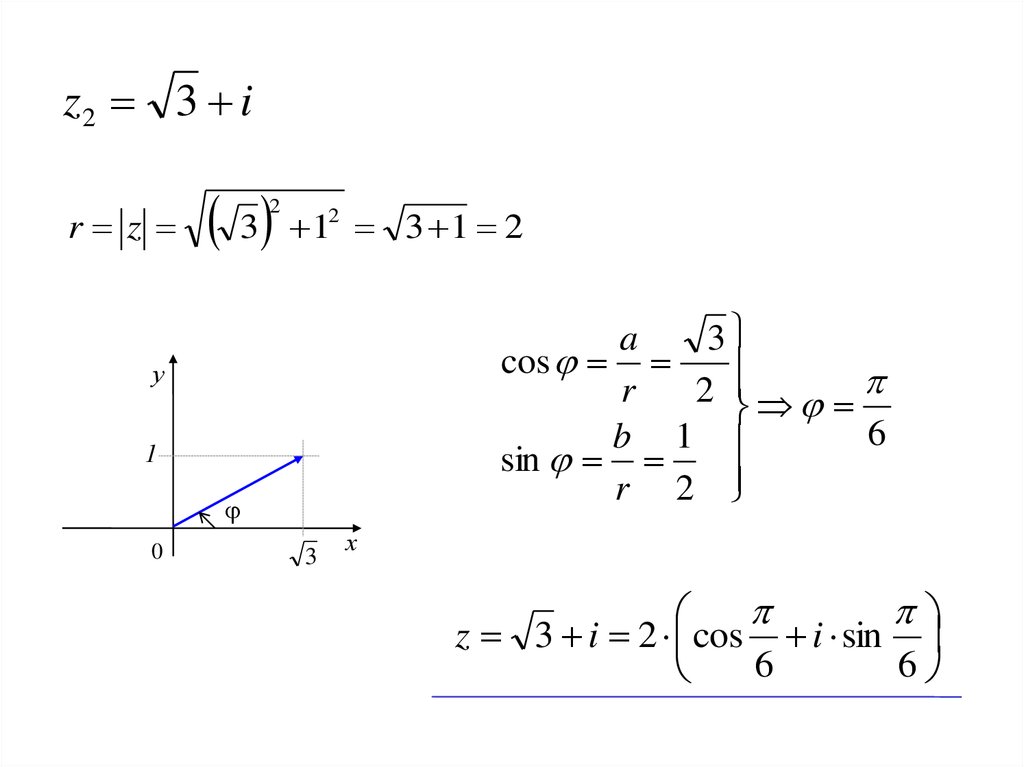
11. 5.Записать число в тригонометрической форме:

5.Записать число z 2 2 3 i
тригонометрической форме:
r z
2
2
2 3
2
2 3
-2
0
4 12 16 4
a 2
1
cos
2
r
4
2
3
b 2 3
3
sin
r
4
2
у
в
х
2
2
z 2 2 3 i 4 cos
i sin
3
3

12. 6. Записать число в алгебраической форме:

z 2 cos i sin
6
6
6. Записать число
в алгебраической форме:
z 2 cos i sin 2 cos i sin
6
6
6
6
3 1
2
i 3 i
2
2

13. 7. Записать число в алгебраической форме:

25
25
z 2 cos
i sin
3
3
7. Записать число
в алгебраической форме:
25 24
8 2 4
3
3
3
3
3
z 2 cos 2 4 i sin 2 4 2 cos i sin
3
3
3
3
1
3
1 i 3
2 i
2
2

14. Действия над комплексными числами в тригонометрической форме Умножение комплексных чисел.

• Пусть
z1 r1 cos 1 i sin 1
z2 r2 cos 2 i sin 2
z1z 2 r1r2 cos 1 i sin 1 cos 2 i sin 2
r1r2 cos 1 cos 2 i sin 1 cos 2 i sin 2 cos 1 i 2 sin 1 sin 2
r1r2 cos 1 cos 2 sin 1 sin 2 i sin 1 cos 2 cos 1 sin 2
r1r2 cos 1 2 i sin 1 2
z1z2 r1r2 cos 1 2 i sin 1 2

15. 8. Найти произведение комплексных чисел:

z1
7
cos 950 i sin 950
2
u
z2 2 cos 650 i sin 650
7
z1 z 2 2 cos 950 650 i sin 950 650
2
7 cos 950 650 i sin 950 650 7 cos 300 i sin 300
3 1 7 3 7
7
i
i
2
2
2 2

16.

Деление комплексных чисел.
z1 r1 cos 1 i sin 1 r1 cos 1 i sin 1 cos 2 i sin 2
z 2 r2 cos 2 i sin 2 r2 cos 2 i sin 2 cos 2 i sin 2
r1 cos 1 cos 2 i sin 1 cos 2 i sin 2 cos 1 i 2 sin 1 sin 2
2
2
r2
cos 2 i sin 2
r1 cos 1 cos 2 sin 1 sin 2 i sin 1 cos 2 cos 1 sin 2
2
2
cos 2 sin 2
r2
r1
cos 1 2 i sin 1 2
r2
z1 r1
cos 1 2 i sin 1 2
z2 r2

17. 9. Найти частное комплексных чисел:

2
z1 cos1500 i sin 1500
3
u
z 2 2 cos 900 i sin 900
z1 2 1 cos1500 i sin 1500 1
0
0
0
0
cos
150
90
i
sin
150
90
0
0
z 2 3 2 cos 90 i sin 90
3
1
1 1
3 1
3
0
0
cos 60 i sin 60
i
i
3
3 2 2 6 6

18. 10. Записать в тригонометрической форме комплексное число:

cos i sin
3
3
z
i 1
3 i

19.

• Пусть
z1 cos
3
i sin
3
z2 3 i
z3 i 1 1 i
Запишем каждое из чисел в тригонометрической форме.
z1 cos i sin cos i sin
3
3
3
3

20.

z2 3 i
r z
3 1
2
2
3 1 2
a
3
cos
r
2
6
b 1
sin
r 2
у
1
0
3
х
z 3 i 2 cos i sin
6
6

21.

z3 1 i
1 2 12
r z
2
a 1
cos
r
3
2
b
1
4
sin
r
2
у
1
-1
0
х
3
3
z 1 i 2 cos
i sin
4
4

22.

cos
i
sin
3
3
z
i 1
3 i cos i sin 2 cos i sin
6
6
3
3
3
3
2 cos
i sin
4
4
11
2 3
3
11
cos
i sin
2 cos
i sin
2 3 6 4
3 6 4
12
12

23. Действия над комплексными числами в тригонометрической форме. Возведение в степень.

z r cos i sin
• Пусть
z r cos n i sin n - формула Муавра
n
n
11. Возвести в четвертую степень комплексное
число:
z 2 cos i sin
3
3
4
4
z 2 cos 4 i sin 4 16 cos
i sin
3
3
3
3
4
4

24. 12. Возвести в степень комплексное число и записать результат в алгебраической форме:

18
2 i
z
2 i 2
Пусть
z1 2i
z2 2 i 2
Запишем каждое из чисел в тригонометрической форме.

25.

z1 2i
r z 02 22 2
у
2
х
z2 2 i 2
r z
у
0
2 2
2
2
2 2 2
3
4
2
2
2
z 2i 2 cos i sin
2
2
0
х
3
3
z 2 i 2 2 cos
i sin
4
4

26. Разделим одно число на другое в тригонометрической форме:

2 cos i sin
z1
2i
2
2
3
3
cos i sin
3
3
z2 2 i 2
2 4
2 4
2 cos
i sin
4
4
cos i sin
4
4
18
А теперь возведём в степень:
18
2 i
z
2 i 2
cos i sin cos 18 i sin 18
4
4
4
4
9
9
cos
i sin
2
2

27. Теперь можно результат записать в алгебраической форме:

Теперь
можно
результат
алгебраической форме:
записать
в
9
9
9
9
z cos
i sin
i sin
cos
2
2
2
2
9 8
4 2 2
2
2
2
2
2
cos 2 2 i sin 2 2 cos i sin
2
2
2
2
0 i

28. Действия над комплексными числами в тригонометрической форме. Извлечение корня.

• Пусть
z r cos i sin
Корнем n-ой степени из числа z (n∈N, n≥2) называется
такое комплексное число u, для которого справедливо
n
u
z
равенство
Корень n-ой степени из комплексного числа z имеет ровно n
значений, которые находятся по формуле:
n
2 k
2 k
z n r (cos i sin ) n r cos
i sin
, k 0,1,2,..., n 1
n
n

29. 13. Найти все значения корня:

6
1
z 1
Пусть
Запишем данное число в тригонометрической форме:
у
r z 12 02 1
0
1
0
х
z 1 cos 0 i sin 0

30.

6
0 2 k
0 2 k
k
k
1 cos 0 i sin 0 cos
i sin
cos i sin
6
6
3
3
6
k 0,1,2,3,4,5
k 0 : u0 cos 0 i sin 0 1
1
3
k 1 : u1 cos i sin
i
3
3 2 2
2
2
1
3
k 2 : u2 cos
i sin
i
3
3
2 2
k 3 : u3 cos i sin 1
4
4
1
3
k 4 : u4 cos
i sin
i
3
3
2 2
5
5 1
3
k 5 : u5 cos
i sin
i
3
3 2 2
у
u2
u1
u3
u0
u4
u5
х

31.

z 1 i 3 0
5
14. Решить уравнение:
z5 1 i 3 z 5 1 i 3
Пусть
z 1 i 3
Запишем данное число в тригонометрической форме:
r z 1
2
у
3 1 2
a
r
b
sin
r
cos
3
0
3
2
1
х
z 1 i 3 2 cos i sin
3
3
1
2
3
3
2

32.

2
k
2
k
5
1 i 3 5 2 cos i sin 5 2 cos 3
i sin 3
3
3
5
5
2 k
2 k
2 cos
i sin
, k 0,1,2,3,4
5
5
15
15
5

33.

2 k
2 k
z 2 cos
i sin
, k 0,1,2,3,4
5
5
15
15
5
k 0 : u0 2 cos i sin
15
15
7
7
5
k 1 : u1 2 cos
i sin
15
15
5
13
13
k 2 : u2 2 cos
i sin
15
15
19
19
k 3 : u3 5 2 cos
i sin
15
15
у
u1
u2
5
25
25
k 4 : u4 5 2 cos
i sin
15
15
u0
u3
u4
х

34.

15. Сделать действия в тригонометрической
форме и ответ записать в алгебраической форме:
7
7
1) 2 cos
i sin
6
6
11
11
2) 3 cos
i sin
3
3
3
Ответ.
2
0 8i
Ответ. 9 9 3 i
2
2

35.

16. Сделать действия над комплексными числами
и ответ записать в тригонометрической форме:
1)
2 cos 400 i sin 400
3 cos 600 i sin 600
Ответ.
2) 2 cos 300 i sin 300 3 cos 700 i sin 700
Ответ.
2
cos 200 i sin 200
3
2 3 cos1000 i sin 1000

36.

17. Представить числа в тригонометрической
форме:
1
3
1) z
i
5 5
3 1
2) z
i
6 6
Ответ.
Ответ.
2
2
2
i sin
cos
5
3
3
1
7
7
i sin
cos
3
6
6

37.

18. Найти z1 z2 ,
форме для чисел
z1
в
z2
1
3
z1
i
5 5
u
тригонометрической
3 1
z2
i
6 6
2
11
11
cos
i
sin
15
6
6
Ответ.
z1 z 2
Ответ.
z1 6
cos i sin
z2 5 2
2

38.

z1
z2
7
19. Найти
в тригонометрической
форме и результат представить в алгебраической
форме, если
1
3
z1
i
5 5
7
Ответ.
u
3 1
z2
i
6 6
z1
67 3
3
7 cos
i sin
5 2
2
z2
67
0 7 i
5

39.

20. Найти все значения корня:
Ответ.
2
2
u0 3 4 cos
i sin
9
9
8
8
3
u1 4 cos
i sin
9
9
14
14
u 2 3 4 cos
i sin
9
9
3
2 2 3i