Похожие презентации:
Гетероскедастичность случайной составляющей
1. Гетероскедастичность случайной составляющей
Гетероскедастичность означает, что ошибкирегрессии имеют непостоянные дисперсии
yi a1 xi1 a2 xi 2
ar 1 xir 1 ar i
i 1, n
D i const
1
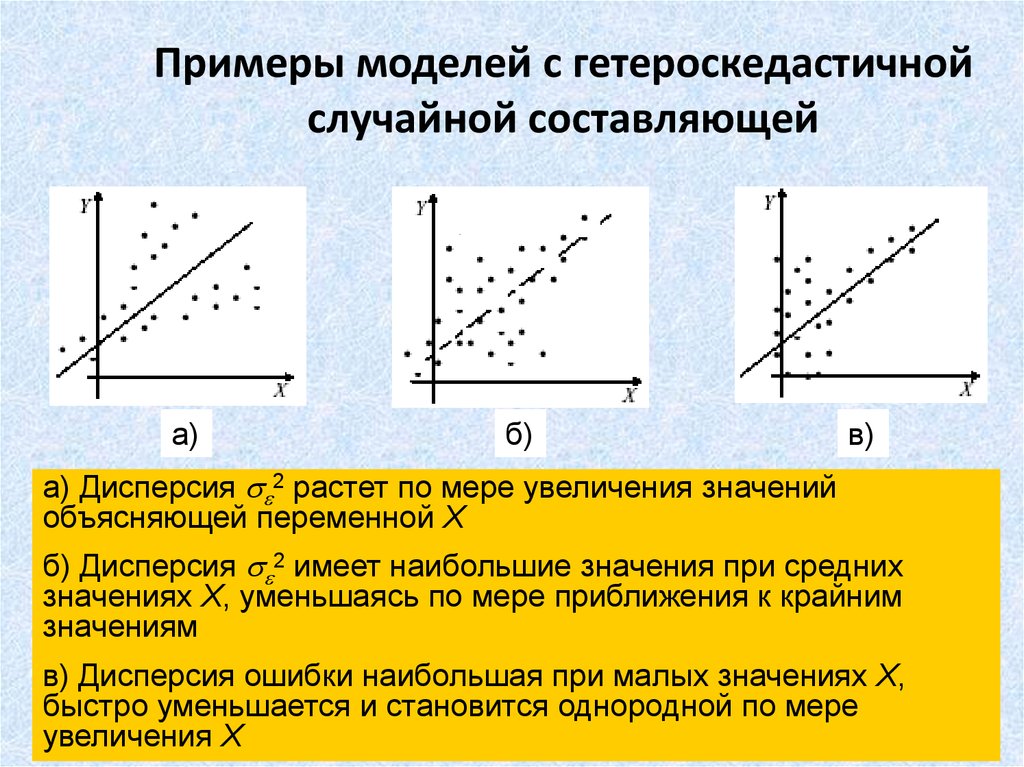
2. Примеры моделей с гетероскедастичной случайной составляющей
а)б)
в)
а) Дисперсия 2 растет по мере увеличения значений
объясняющей переменной X
б) Дисперсия 2 имеет наибольшие значения при средних
значениях X, уменьшаясь по мере приближения к крайним
значениям
в) Дисперсия ошибки наибольшая при малых значениях X,
быстро уменьшается и становится однородной по мере
увеличения X
2
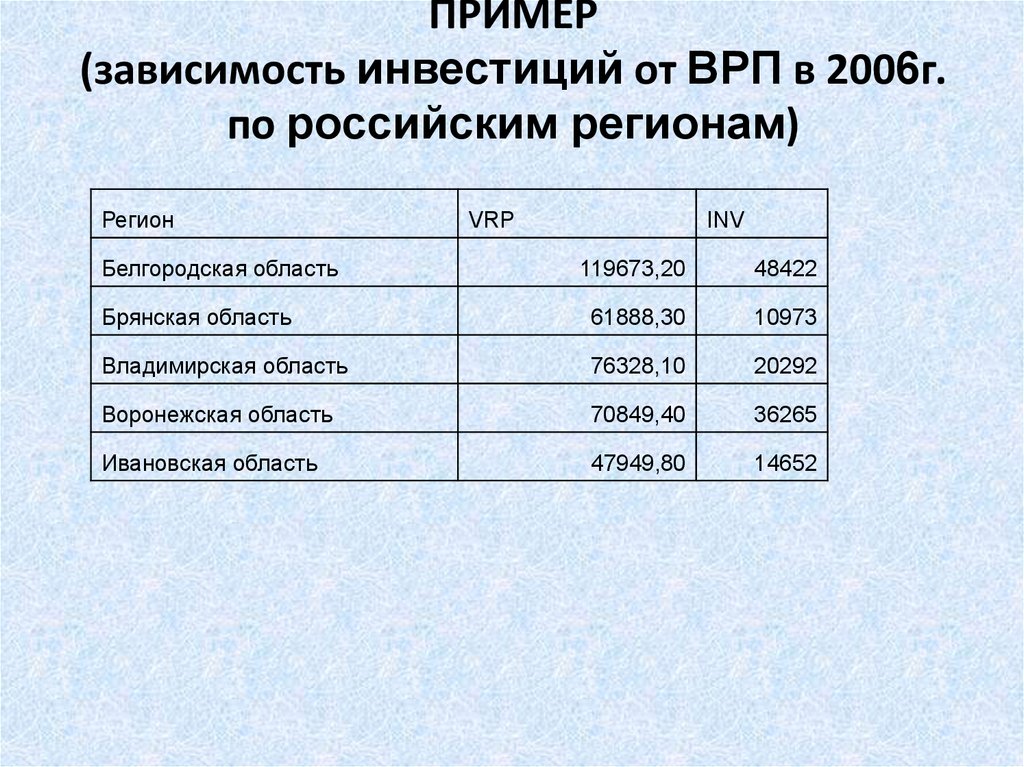
3. ПРИМЕР (зависимость инвестиций от ВРП в 2006г. по российским регионам)
РегионБелгородская область
VRP
INV
119673,20
48422
Брянская область
61888,30
10973
Владимирская область
76328,10
20292
Воронежская область
70849,40
36265
Ивановская область
47949,80
14652
4. ПРИМЕР (зависимость инвестиций от ВРП в 2006г. по российским регионам)
Коэффициенты
Станда
ртная
ошибка
Yпересечение
5164,439
11352,89 0,454901 0,650428
VRP
0,345983 0,070519 4,906268
INV 0,346 VRP 5164
tстатис
тика
PЗначени
е
4,88E-06
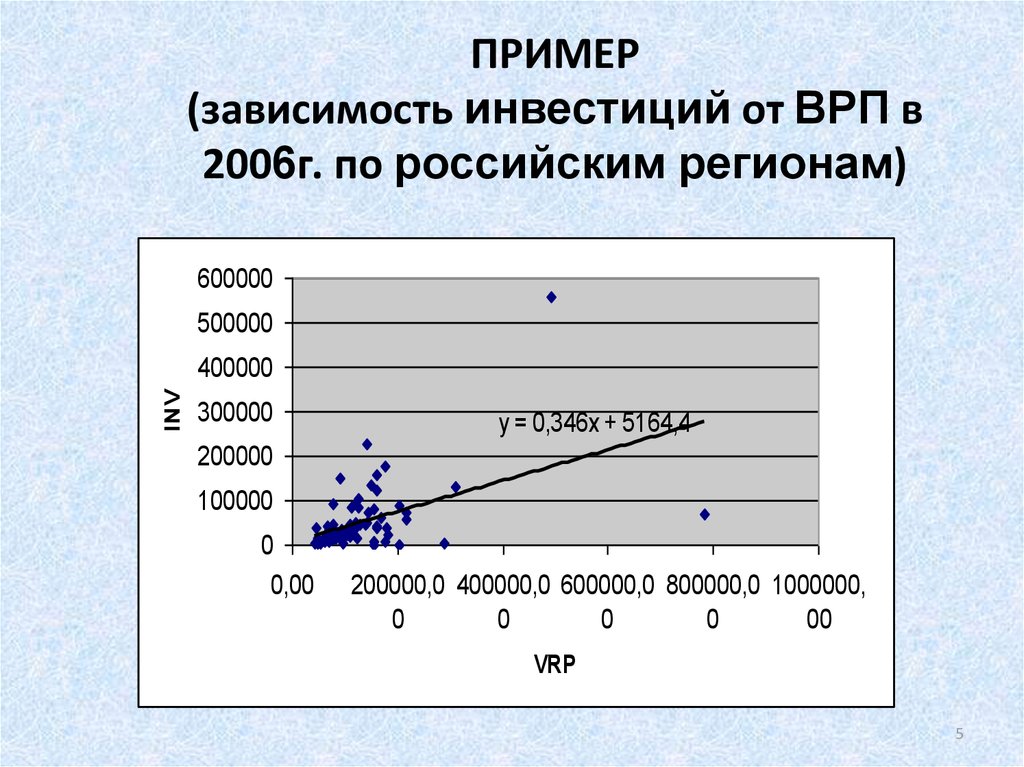
5. ПРИМЕР (зависимость инвестиций от ВРП в 2006г. по российским регионам)
600000500000
INV
400000
300000
y = 0,346x + 5164,4
200000
100000
0
0,00
200000,0 400000,0 600000,0 800000,0 1000000,
0
0
0
0
00
VRP
5
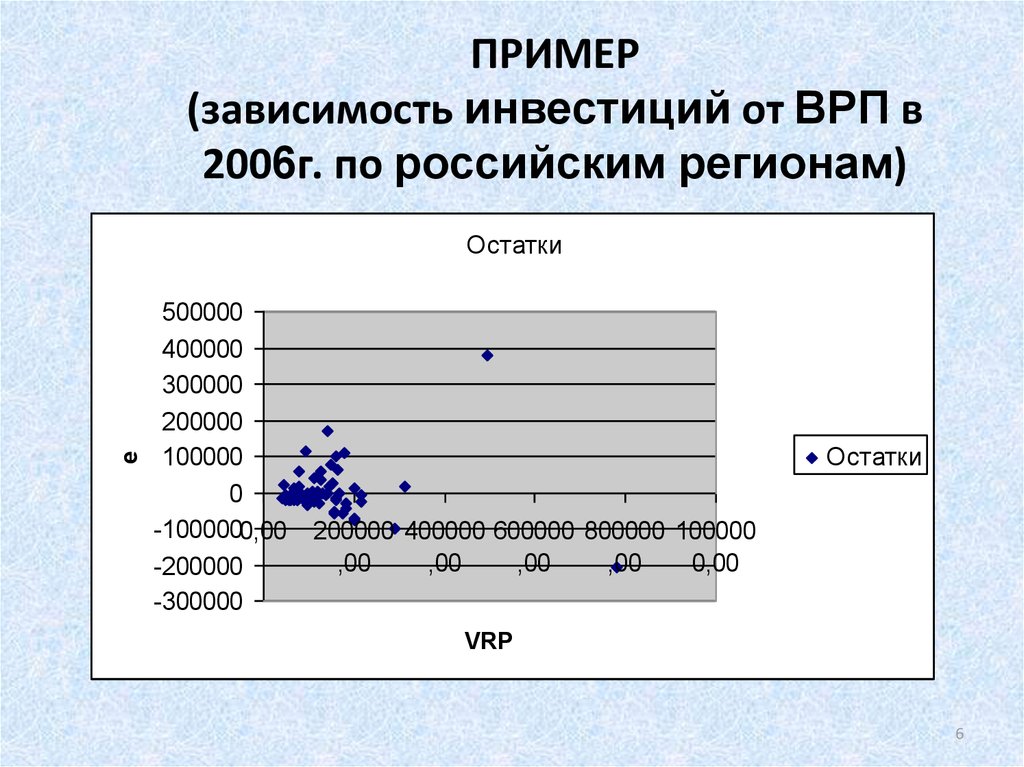
6. ПРИМЕР (зависимость инвестиций от ВРП в 2006г. по российским регионам)
eОстатки
500000
400000
300000
200000
100000
0
-1000000,00
-200000
-300000
Остатки
200000 400000 600000 800000 100000
,00
,00
,00
,00
0,00
VRP
6
7.
Наиболее распространенный случай истиннойгетероскедастичности: дисперсия растет с
ростом одного из факторов.
8. ПОСЛЕДСТВИЯ ГЕТЕРОСКЕДАСТИЧНОСТИ
1. Обычная МНК оценка несмещеннаясостоятельная, но неэффективная.
2. Стандартные ошибки коэффициентов
(вычисленные в предположении.
гомоскедастичности) будут занижены. Это приведет
к завышению t-статистик и даст
неправильное (завышенное) представление о
точности оценок.
8
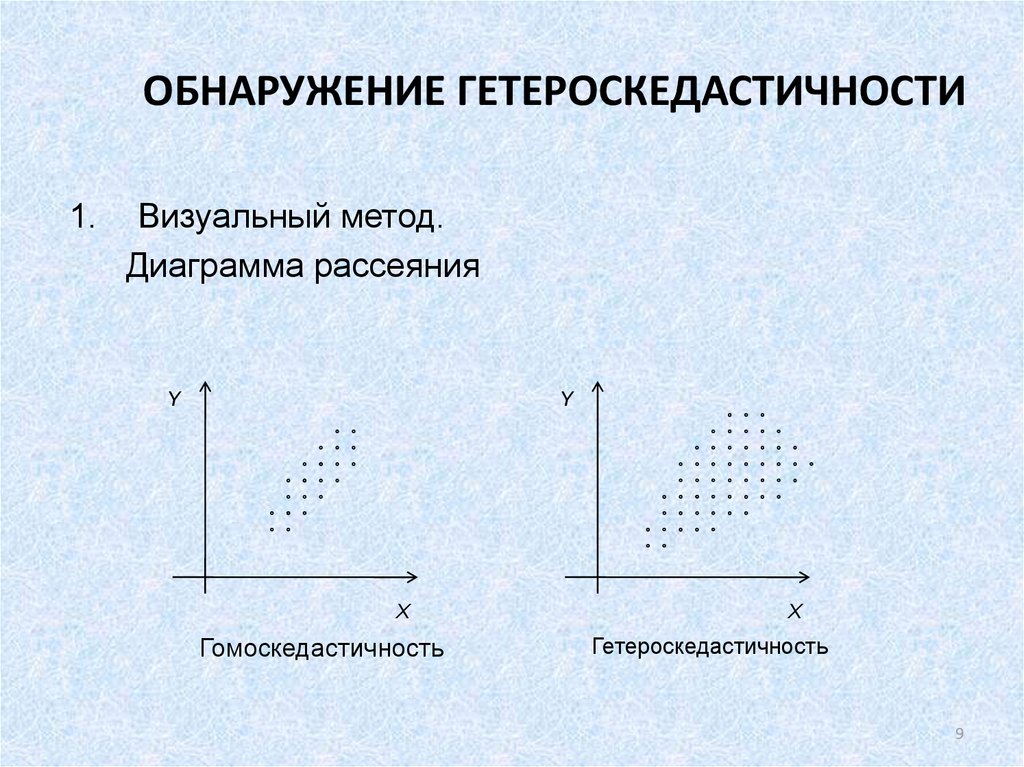
9. ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
1.Визуальный метод.
Диаграмма рассеяния
Y
Y
X
Гомоскедастичность
X
Гетероскедастичность
9
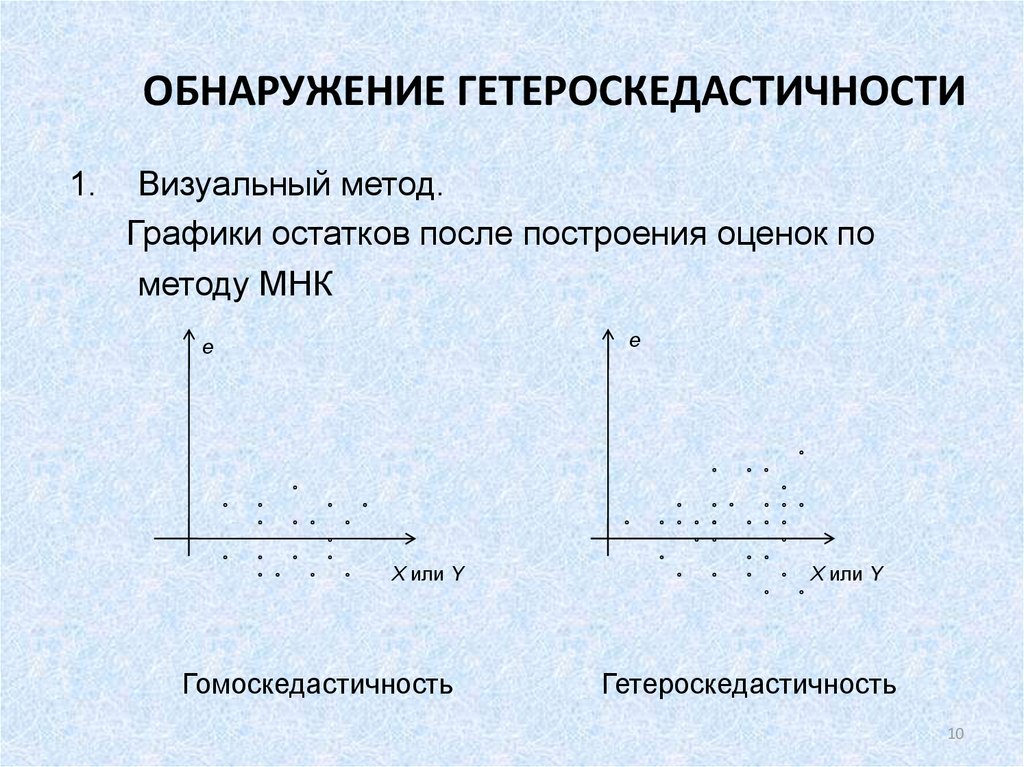
10. ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
1.Визуальный метод.
Графики остатков после построения оценок по
методу МНК
e
e
X или Y
Гомоскедастичность
X или Y
Гетероскедастичность
10
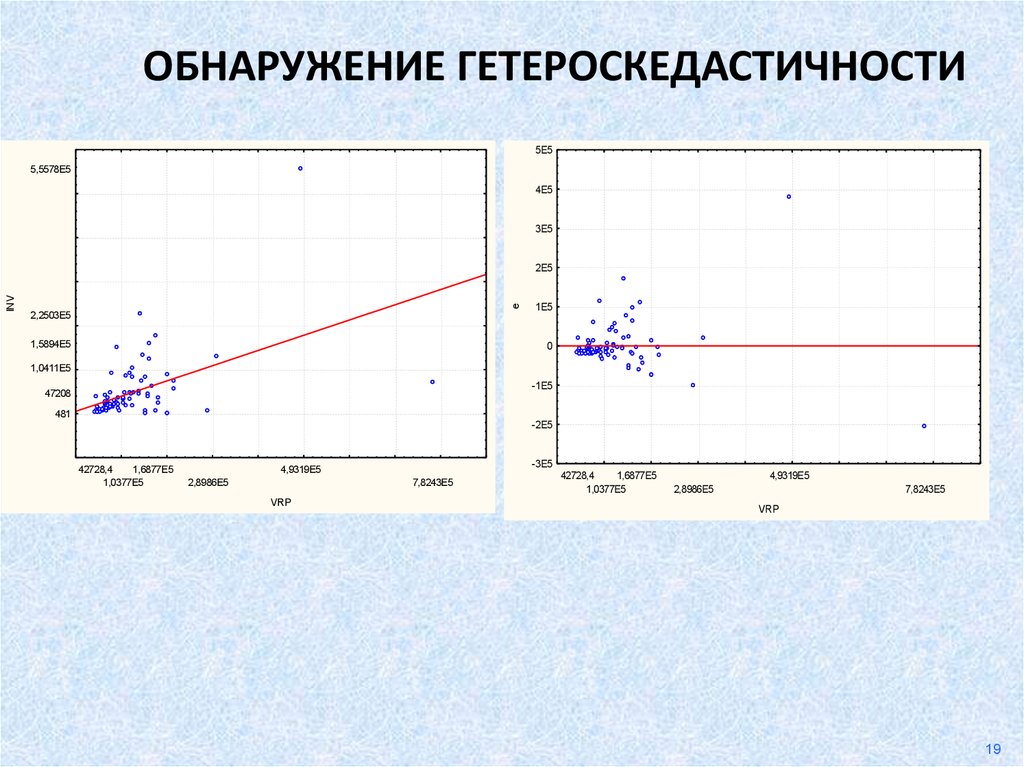
11.
ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ5E5
5,5578E5
4E5
3E5
e
INV
2E5
2,2503E5
1,5894E5
1E5
0
1,0411E5
-1E5
47208
481
-2E5
42728,4
1,6877E5
1,0377E5
-3E5
4,9319E5
2,8986E5
7,8243E5
VRP
42728,4
1,6877E5
1,0377E5
4,9319E5
2,8986E5
7,8243E5
VRP
19
12. ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
Тесты:1. Тест ранговой корреляции Спирмена.
2. Тест Глейзера.
3. Тест Голдфелда-Квандта.
4. Тест Уайта.
В специализированных эконометрических пакетах эти тесты есть
12
13. Устранение ГЕТЕРОСКЕДАСТИЧНОСТИ
Использовать обобщенный методнаименьших квадратов
В этом методе предполагается, что
стандартное отклонение остатков
пропорционально одной из объясняющих
переменных
Например,
INVi a1VRPi a2 i , i 1, n
D i
2
i
i k VRPi , i 1, n
13
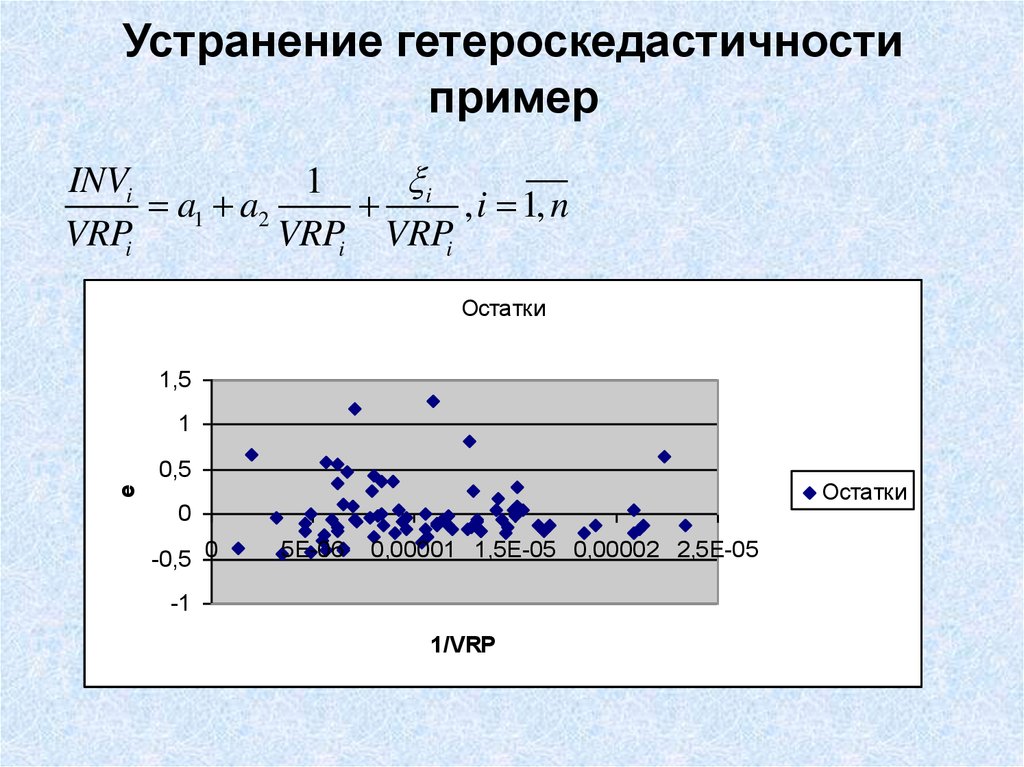
14. Устранение гетероскедастичности пример
INVi a1 VRPi a2 i , i 1, nДелим уравнение на ВРП
INVi
i
1
a1 a2
, i 1, n
VRPi
VRPi VRPi
15. Устранение гетероскедастичности пример
INVii
1
a1 a2
, i 1, n
VRPi
VRPi VRPi
Создаем новые переменные
INV
1
,
VRP VRP
Регион
Белгородская область
VRP
INV
INV/VRP
1/VRP
119673,20
48422
0,40
8,36E-06
Брянская область
61888,30
10973
0,18
1,62E-05
Владимирская область
76328,10
20292
0,27
1,31E-05
Воронежская область
70849,40
36265
0,51
1,41E-05
Ивановская область
47949,80
14652
0,31
2,09E-05
Калужская область
83817,40
16268
0,19
1,19E-05
16. Устранение гетероскедастичности пример
INVii
1
a1 a2
, i 1, n
VRPi
VRPi VRPi
Коэффициент
ы
Стандартная
ошибка
t-статистика
Y-пересечение
0,491025
0,0864
5,683151
2,13E-07
1/VRP
-11337,2
7354,391
-1,54156
0,127178
INV
1
0,5 11,337
,
VRP
VRP
INV 0,5 VRP 11,337
P-Значение
17. Устранение гетероскедастичности пример
INVii
1
a1 a2
, i 1, n
VRPi
VRPi VRPi
Остатки
1,5
1
0,5
e
Остатки
0
-0,5 0
5E-06
0,00001 1,5E-05 0,00002 2,5E-05
-1
1/VRP
18. Гетероскедастичность как результат неправильной спецификации модели (ложная гетероскедастичность).
1) В модель не включен фактор, существенно влияющий на объясняемуюпеременную.
Пример. Предполагается, что имеется зависимость импорта M от ВВП
страны (GDP) и отношение отечественных цен к мировым (PR).
M i a1 GDPi a2 PRi a3 i
Исследователь рассчитывает сокращенный вариант модели:
M i a2 PRi a3 i
Остатки в такой модели покажут на гетероскедастичность, так как будут
зависеть от GDP
i a1 GDPi i
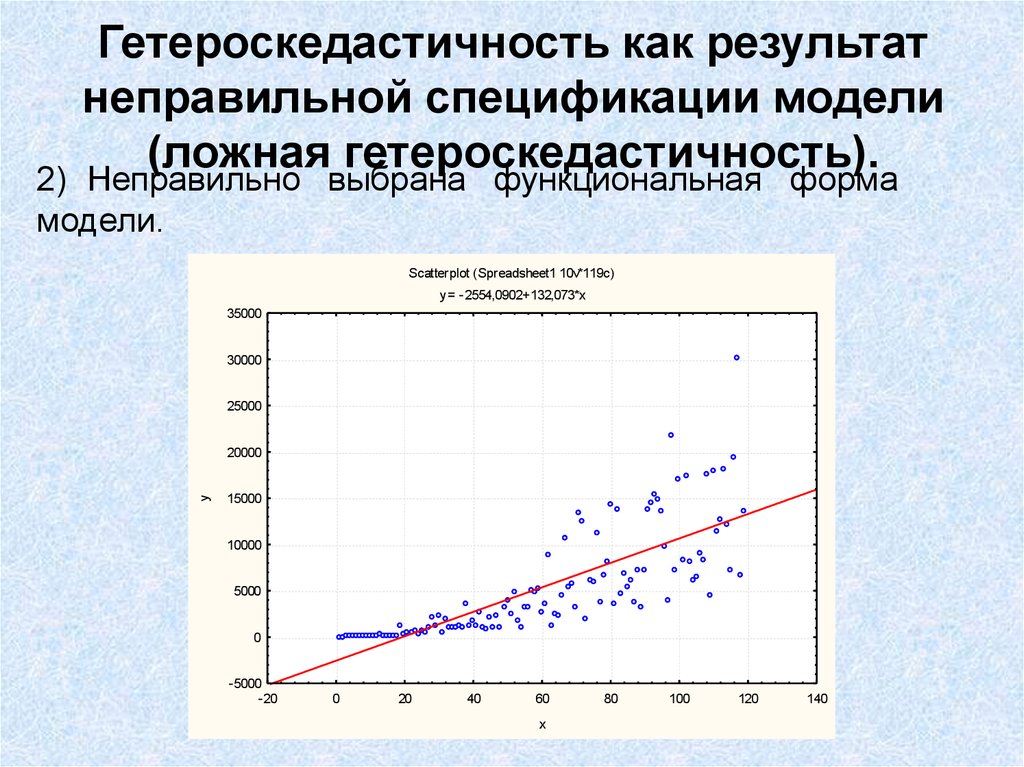
19. Гетероскедастичность как результат неправильной спецификации модели (ложная гетероскедастичность).
2) Неправильно выбрана функциональная формамодели.
Scatterplot (Spreadsheet1 10v*119c)
y = -2554,0902+132,073*x
35000
30000
25000
y
20000
15000
10000
5000
0
-5000
-20
0
20
40
60
x
80
100
120
140
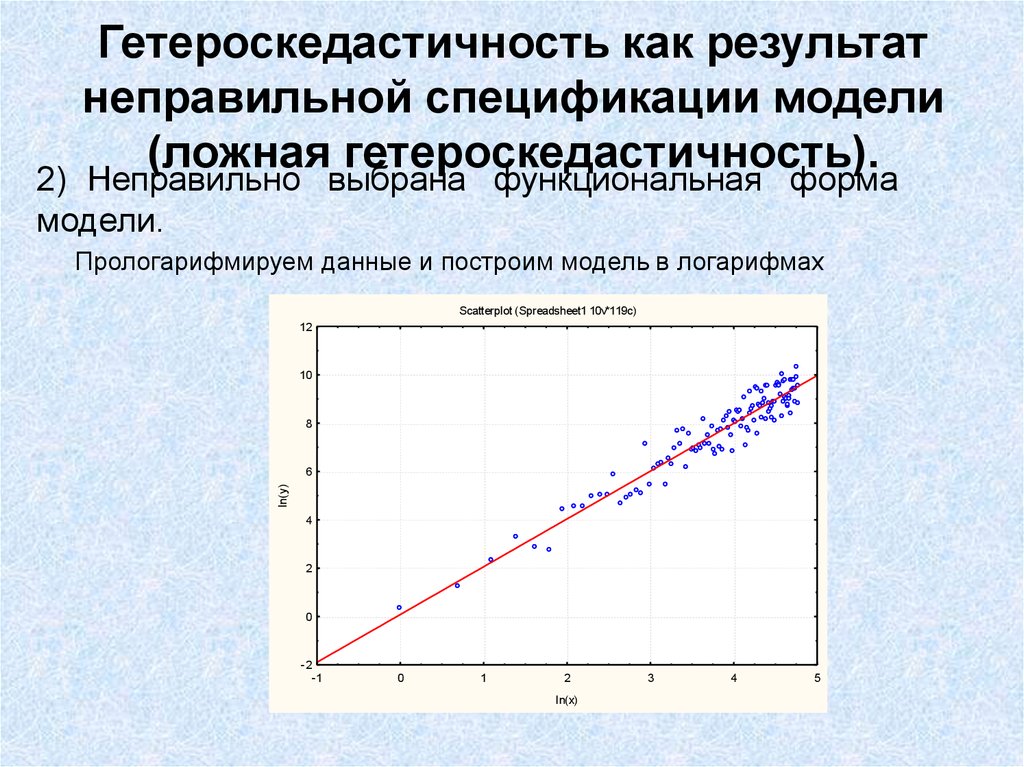
20. Гетероскедастичность как результат неправильной спецификации модели (ложная гетероскедастичность).
2) Неправильно выбрана функциональная формамодели.
Прологарифмируем данные и построим модель в логарифмах
Scatterplot (Spreadsheet1 10v*119c)
12
10
8
ln(y)
6
4
2
0
-2
-1
0
1
2
ln(x)
3
4
5










 Математика
Математика Экономика
Экономика








