Похожие презентации:
Задача Эйлера
1.
Задача Эйлера2.
Леонард ЭйлерШвейцарский, немецкий и
российский математик и
механик, внёсший
фундаментальный вклад в
развитие этих наук. Эйлер автор более чем 850 работ
по математическому
анализу, дифференциальной
геометрии, теории чисел,
приближённым
вычислениям, небесной
механике, математической
физике, оптике, баллистике,
кораблестроению, теории
музыки и другим областям.
Он глубоко изучал
медицину, химию, ботанику,
воздухоплавание, теорию
музыки, множество
европейских и древних
языков.
3.
Доказать, что в произвольномтреугольнике:
1) Точки, симметричные точке Н
пересечения высот (или их
продолжений) относительно сторон
треугольника и их середин, лежат на
описанной окружности;
4.
Доказать, что в произвольномтреугольнике:
2) Середины сторон, основания высот и
середины отрезков, соединяющих точку
Н с вершинами, лежат на одной
окружности, центром которой является
середина отрезка, соединяющего точку
Н с центром описанной окружности, а
ее радиус в два раза меньше радиуса
описанной окружности (эта окружность
называется окружностью Эйлера);
5.
Доказать, что в произвольномтреугольнике:
3)Точка пересечения медиан лежит на
отрезке, соединяющем точку Н с
центром описанной окружности, и делит
этот отрезок в отношении 1:2, считая от
центра описанной окружности (прямая,
на которой лежат четыре точки — точка
Н, точка пересечения медиан, центр
описанной окружности и центр
окружности Эйлера, называется прямой
Эйлера);
6.
Доказать, что в произвольномтреугольнике:
4)Точки, симметричные центру
описанной окружности относительно
прямых, содержащих средние линии
треугольника, лежат на окружности
Эйлера.
7.
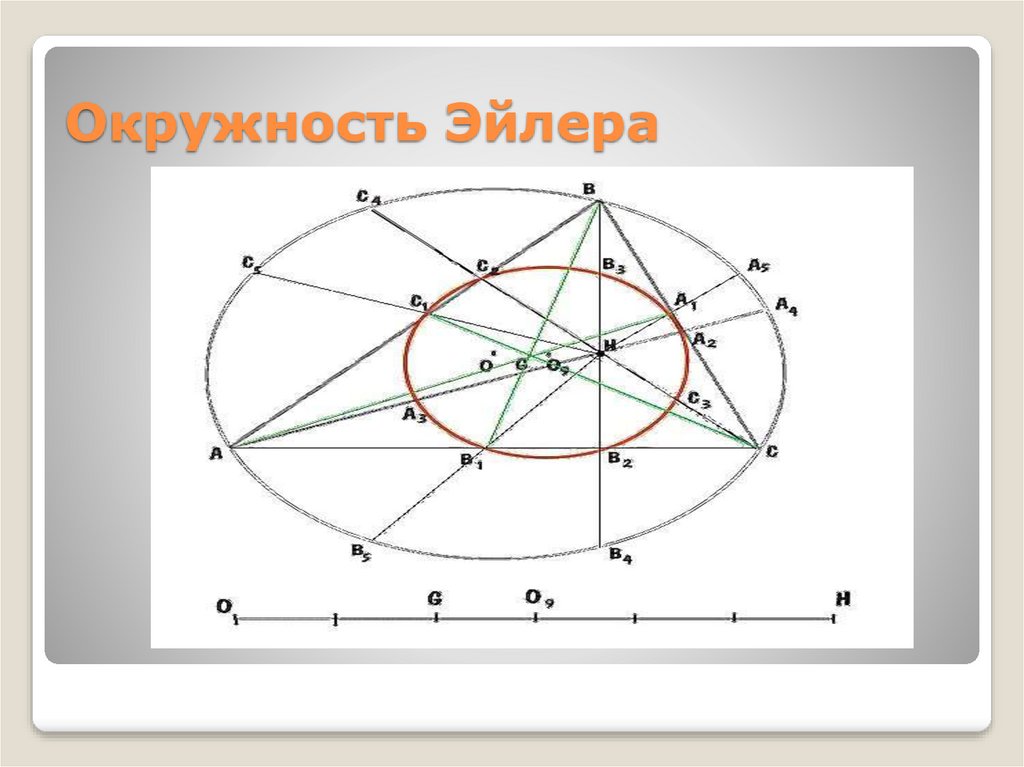
РешениеПусть ABC — данный треугольник (рис. 217).
Условимся о следующих обозначениях: G — точка
пересечения медиан, О — центр описанной
окружности, R — ее радиус, А19 Вг и Сх — середины
сторон ВС, СА и АВ, А2, В2 и С2 — основания высот,
проведенных к этим сторонам, А3, В3 и С3 —
середины отрезков АН, ВН и СН, А4, В4 и С4 —
точки, симметричные точке Н относительно сторон
треугольника, А5, В5 и С5 — точки, симметричные
точке Н относительно середин этих сторон, Ае, Б6 и
С6 — точки, симметричные точке О относительно
прямых ВгС19 СхАг и АХВХ (на рисунке они не
отмечены). Приступим теперь к решению задачи.
8.
Решение1) Если один из углов треугольника ABC, например угол А, —
прямой, то точки Н, В4 и С4 совпадают с точкой А, точка В5 — с
точкой С, а точка С5 — с точкой В. Поскольку ZBA4C = ZBAbC = ZA =
90°, то точки А, А4 и Аъ лежат на окружности с диаметром ВС (см. п.
88). Таким образом, точки А4,
А5, В4, В5, С4, С5 лежат на окружности, описанной около
треугольника ABC.
Допустим, что треугольник ABC не является прямоугольным.
Поскольку ZAB2H = ZAC2H = 90°, то точки В2 и С2 лежат на
окружности с диаметром АН (см. п. 88). Следовательно, вписанные
по отношению к этой окружности углы В2АС2 и В2НС2, а значит, и
углы ВАС и ВНС, либо равны, либо составляют в сумме 180°. И в
том, и в другом случае sin ZBHC = sin ZBAC.
Пусть Rx — радиус окружности, описанной около треугольника НВС.
В соответствии с теоремой 2 из п. 92 ВС = 2RX sin ZBHC = 2R sin
ZBAC. Ho sin ZBHC = = sin ZBAC. Значит, Rx = R. Из этого следует,
что окружности, описанные около треугольников ABC и НВС,
симметричны относительно прямой ВС и относительно середины
отрезка ВС. Точка Н лежит на окружности, описанной около
треугольника НВС. Следовательно, симметричные ей точки А4 и А5
лежат на окружности, описанной около треугольника ABC.
Аналогично доказывается, что точки Б4, Б5, С4 и С5 также лежат на
этой окружности.
9.
Решение2)Рассмотрим центральное подобие с центром Н и
коэффициентом i. При этом подобии описанD
ная окружность переходит в окружность радиуса —,
Li
центр 09 которой является серединой отрезка ОН (см. рис. 217),
а точки А5, Б5, С5, А4, Б4, С4, А, Б, С описанной окружности
переходят соответственно в точки Ах, Би Cj (середины сторон),
А2, Б2 и С2 (основания высот), А3, Б3 и С3 (середины отрезков АН,
ВН, СН). Следовательно, точки А], Бх, Сх, А2, Б2, С2, А3, Б3, С3
лежат на окружности с центром 09 радиуса у. Утверждение
доказано.
10.
Решение3)Рассмотрим теперь центральное подобие
с центром G и коэффициентом - Медианы треугольника АБС делятся точкой G в отношении 1 : 2, поэтому при
рассматриваемом центральном подобии вершины А, Б и С
перейдут в середины Ах, Бх и Сх противоположных сторон.
Следовательно, прямые, содержащие высоты треугольника,
перейдут в прямые, перпендикулярные к его сторонам и
проходящие через их середины, т. е. в серединные
перпендикуляры к сторонам. Поэтому точка Н перейдет в центр
О описанной окружности. Это означает, что точка G лежит на
отрезке ОН и делит его в отношении 1 : 2, считая от точки О, что
и требовалось доказать.
11.
Решение4)Как только что отмечалось, при центральном подобии с
центром G и коэффициентом вершины А, Б и С переходят в середины Ах, Бх и Сх
противоположных сторон, а точка Н переходит в точку О. Из
этого следует, что: а) окружность, описанная около
треугольника АБС, переходит в окружность Эйлера; б) точки А4,
В4 и С4 описанной окружности, симметричные точке Н
относительно прямых ВС, СА и АВ, переходят в точки А6, Б6 и С6
окружности Эйлера, симметричные точке О относительно прямых
ВгС19 СгА2 и АХВХ. Таким образом, точки А6, Б6 и С6 лежат на
окружности Эйлера.












 Математика
Математика








