Комбинаторные задачи. Комбинации с учетом и без учета порядка

1.

Урок №1
МБОУ СОШ № 167
г.НОВОСИБИРСКА
УЧИТЕЛЬ МАТЕМАТИКИ
ВАСИЛЕВА МАРИНА ЮРЬЕВНА

2.

ТЕОРИЯ ВЕРОЯТНОСТЕЙ В КУРСЕ 9 КЛАССА
№урока Тема урока
1
Проверка знаний
Комбинаторные задачи.
Комбинации с учетом и без учета порядка
2
3
4
Самостоятельная
работа
5
Размещение из N элементов по k (k ≤ n)
6
Комбинаторные задачи на нахождение числа
размещений из п элементов по k (k ≤ п)
7
Сочетание из n элементов по k (k ≤ n)
8
Комбинаторные задачи на нахождение числа
перестановок из п элементов, сочетаний
и размещений из п элементов по k (k ≤ п)
Самостоятельная
работа
Проверочная
работа

3.

№урока Тема урока
9
Относительная частота случайного события
10
Вероятность случайного события
Проверка знаний
11
12
Геометрическое определение вероятности
Самостоятельная
работа
13
Комбинаторные методы решения
вероятностных задач
Проверочная
работа
14
Обобщающий урок по теме «Элементы
комбинаторики и теории вероятностей»
15
Контрольная работа.

4.

Цели:
•Усвоить
понятие комбинаторной
задачи
•Научиться решать комбинаторные
задачи полным перебором
вариантов, а также с помощью
графов
•Развивать умения наблюдать,
анализировать, обобщать
математические ситуации

5.

Задача №1. Волк, коза и капуста
Некий человек должен был перевезти в лодке
через реку волка, козу и капусту. В лодке мог
поместиться только один человек, а с ним или
волк, или коза, или капуста. Но если оставить
волка с козой без человека, то волк съест козу,
если оставить козу с капустой, то коза съест
капусту, а в присутствии человека никто никого
не ест. Как перевезти груз через реку?

6.

7.

В математике существует немало задач, в которых требуется из
имеющихся элементов составить различные наборы, подсчитать
количество всевозможных комбинаций элементов,
образованных по определенному правилу. Такие задачи
называются комбинаторными, а раздел математики,
занимающейся решением этих задач, называется
комбинаторикой (от лат. combinare, которое означает «соединять,
сочетать»).
С комбинаторными задачами люди имели дело еще в глубокой
древности, когда, например, они выбирали наилучшее
расположение воинов во время охоты, придумывали узоры на
одежде или посуде. Позже появились нарды, шахматы. Как ветвь
математики комбинаторика возникла только в XVII в. В
дальнейшем полем для приложения комбинаторных методов
оказались биология, химия, физика. И, наконец, роль
комбинаторики коренным образом изменилась с применением
компьютеров: она превратилась в область, находящуюся на
магистральном пути развития науки.

8.

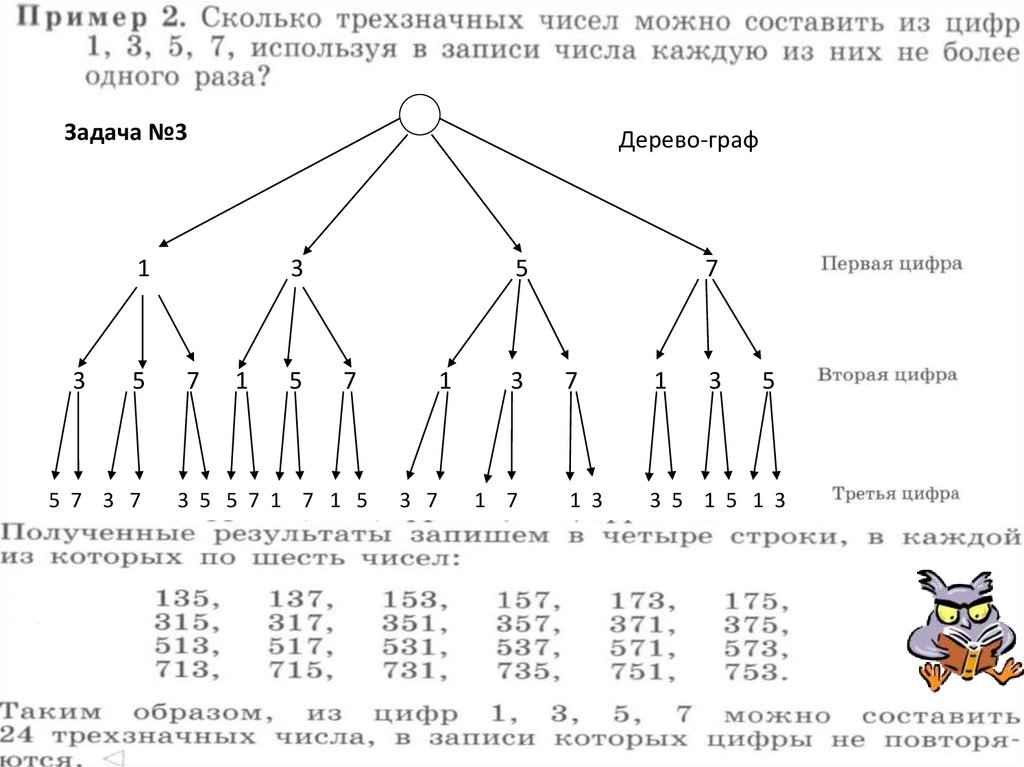
Задача №2

9.

Задача №3
Дерево-граф
1
3
5
5 7 3 7
3
7
1
5
5
7
3 5 5 7 1 7 1 5
1
3 7
3
1 7
7
7
1
3
5
1 3
3 5 1 5 1 3

10.

11.

12.

З а д а ч а№4. В столовой предлагают два первых блюда: щи и борщ; три вторых
блюда: рыба, гуляш и плов; два третьих: компот и чай. Перечислите все возможные
варианты обедов из трех блюд. Проиллюстрируйте ответ, построив дерево
возможных вариантов.
Решение
Первое
блюдо
Второе
блюдо
щи
рыба
компот
чай
гуляш
компот
чай
плов
компот
чай
обеды
борщ
О т в е т: 12 вариантов.
(2*3*2)
Третье
блюдо
рыба
компот
чай
гуляш
компот
чай
плов
компот
чай
Варианты
обеда
щ – р – к (1)
щ – р – ч (2)
щ – г – к (3)
щ – г – ч (4)
щ – п – к (5)
щ – п – ч (6)
б – р – к (7)
б – р – ч (8)
б – г – к (9)
б – г – ч (10)
б – п – к (11)
б – п – ч (12)

13.

Ответ:12.
(3*4)

14.

Решите на доске
и в тетрадях:
№ 715
№ 716
№ 717
№ 718
№ 720

15.

Итоги урока
.
– Какие задачи называются
комбинаторными?
– Приведите примеры ситуаций
выбора комбинаций с учетом и без
учета порядка элементов.
– В чем сущность способа полного
перебора вариантов?
– Из чего состоит граф (граф-дерево)
возможных вариантов?

16.

Домашнее
задание:
№ 714, № 719,
№ 721, № 729.

17.

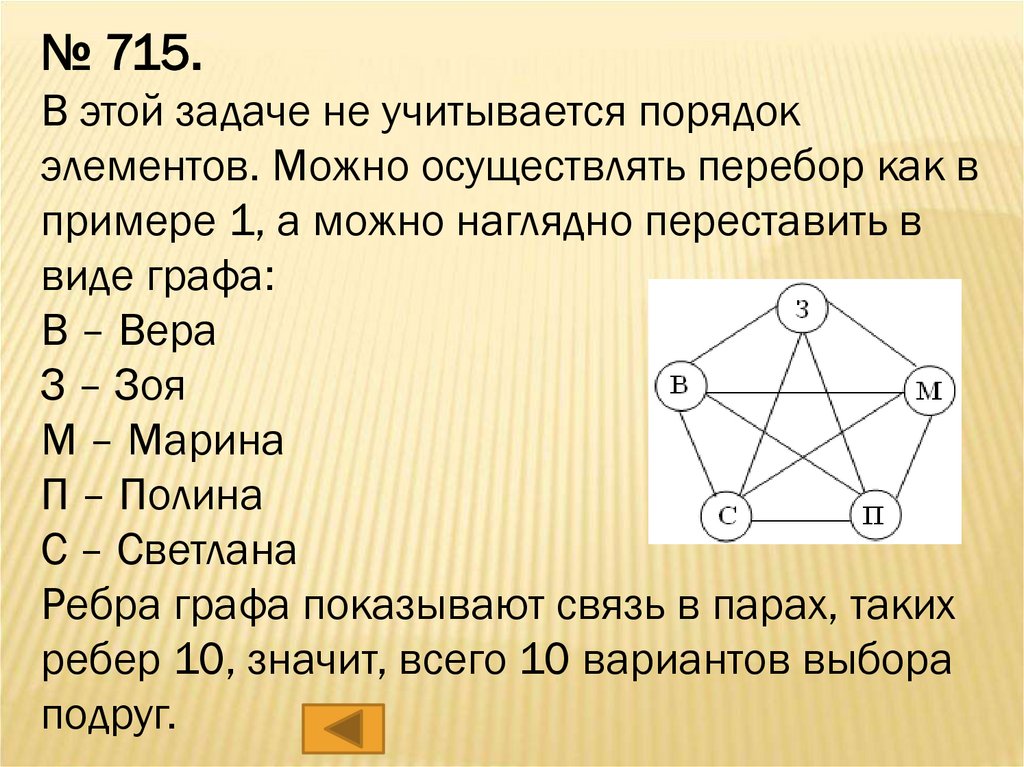
№ 715.
В этой задаче не учитывается порядок
элементов. Можно осуществлять перебор как в
примере 1, а можно наглядно переставить в
виде графа:
В – Вера
З – Зоя
М – Марина
П – Полина
С – Светлана
Ребра графа показывают связь в парах, таких
ребер 10, значит, всего 10 вариантов выбора
подруг.

18.

№ 716.
В этой задаче при выборе пар входов порядок
выбора имеет значение: АВ означает, что
посетитель вошел через А, а вышел через В, а ВА
означает, что вошел через В, а вышел через А.
Фиксируем каждый вход по очереди и
дописываем к нему в пару оставшиеся:
А: АВ, АС, АD;
В: ВА, ВС, ВD;
С: СА, СВ, СD;
D: DA, DB, DC.
Итого – 12 вариантов.

19.

№. 718, № 720.
При решении этих задач
следует обратить внимание
учащихся, что если мы из цифр
составляем двузначное
(трехзначное) число, то нуль не
может стоять на первом месте.

20.

№ 717.
Заметим, что для указания способа
раскладки яблок в две вазы достаточно
указать способ заполнения одной вазы,
поскольку все, что не попадает в первую
вазу, попадает во вторую.
Вообще, во всех случаях, когда п элементов
нужно разбить на 2 группы, при подсчете
количества способов разбиения достаточно
подсчитать число способов формирования
одной половины.

21.

ПРИ ПОДГОТОВКЕ ПРЕЗЕНТАЦИЙ ИСПОЛЬЗОВАНЫ
МАТЕРИАЛЫ :
•Алгебра. 9 класс: поурочные планы по учебнику Ю. Н.
Макарычева (компакт-диск) – издательство «Учитель», 2010
•Алгебра: для 9 класса общеобразовательных учереждений/
Ю. Н.Макарычев, Н.Г. Миндюк, К.И. Нешков, С. Б. Суворова;
под редакцией С.А. Телековского.-М.: Просвещение, 2009.
•345×360на ux1.eiu.eduJPG, 21 КБ
•621×576на activerain.comGIF, 23 КБ