Упрощение выражений. 5 класс

1.

«Упрощение выражений»
презентация к уроку математики
в 5 классе
Автор: учитель математики
Гунякина Л.В.
МОУ «Чернослободская ош»
Шацкого района Рязанской области.

2.

Игра на концентрацию внимания
«Птица в клетке»
1
2
3
7
8
13
14
19
25
31
20
5
6
10
11
12
15 16
17
21 22
23
26 27
32
4
28
33 34
29
35
18
24
30
36

3.

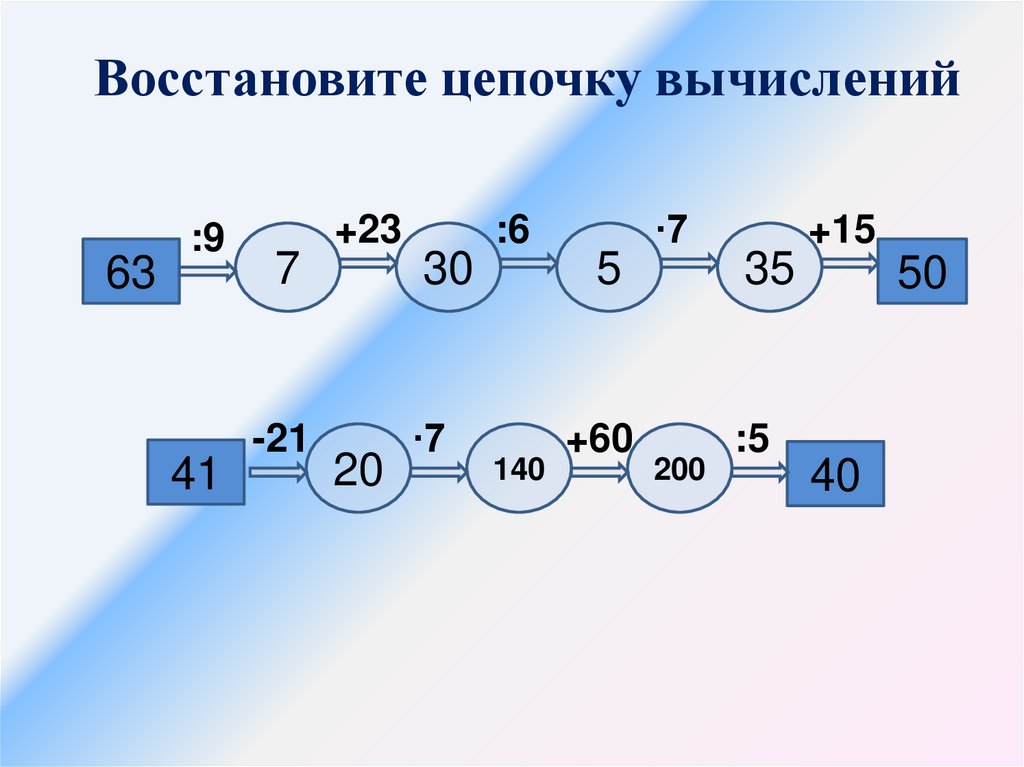
Восстановите цепочку вычислений
63
:9
41
+23
7
-21
:6
30
20
∙7
5
140
+60
∙7
200
+15
35
:5
50
40

4.

Вычислите:
90
45
75
18
36
3
8
64

5.

Математический диктант
1. Запишите буквами переместительное
свойство сложения.
2. Запишите буквами переместительное
свойство умножения.
3. Запишите буквами сочетательное
свойство сложения.
4. Запишите буквами сочетательное
свойство умножения.
5. Решите уравнения:
6. Упростите:
4х=32; 240/у = 24.
у*7*5 ; 5*х*4.

6.

Проверка
1) а + в = в + а
2) а ·в = в · а
3) (а+в)+с = а+(в+с)
4) (а·в)·с = а·(в·с)
5) Х=8;
У=10
6) 35у;
20х

7.

Вычислите:
56 · 4 =

8.

Расскажите, как вы вычисляли
56 · 4 = (50 + 6) · 4 = 50 ·4 + 6·4 = 224
50
6

9.

28 ноября.
Классная работа.
Упрощение выражений.

10.

Цель урока:
Учиться упрощать выражения, применяя
распределительное свойство умножения.

11.

Для упрощений выражений часто
используют свойства умножения:
Переместительное свойство:
а·b = b·а
Сочетательное свойство:
a·(b·c) = (a·b)·c

12.

Сочетательные (а·в)·с = а·(в·с)
и переместительные а ·в = в · а
свойства умножения используются и при
упрощении буквенных выражений:
6 • a • 2 = 6 • 2 • a = 12a
2 • a • 4 • b = 2 • 4 • a • b = 8ab
5b + 8b = (5 + 8) • b = 13b
14y - 12y = (14 - 12) • y = 2y

13.

Применение переместительного и
сочетательного свойств умножения
для упрощения выражений:
3х ∙ 6 ∙ 10 =
(3 ∙ 6 ∙ 10)х = 180х
4 ∙ 2у ∙ 15 =
(4 ∙ 2 ∙ 15) у = 120у

14.

Устно упростите выражения:
15a ∙ 4 =
3b ∙ 12 =
18 ∙ 5b =
11a ∙ 7 =
16 ∙ d ∙ 3 =
x∙5∙4∙6=
60а
36b
90b
77a
48d
120x

15.

Задание :Как найти сумму всех
квадратов?
(4 + 2) · 3 = 6 · 3 = 18

16.

Задание :Как можно вычислить
количество другим способом?
4· 3 + 2 · 3 = 12 + 6 =18

17.

(4 + 2) · 3 = 6 · 3 = 18
4· 3 + 2 · 3 = 12 + 6 =18
Умножение суммы на число

18.

Распределительное свойство
умножения относительно
сложения

19.

Задание :Как можно узнать, на
сколько желтых квадратов больше,
чем зеленых?
(4 - 2)*3=4*3 - 2*3=12 – 6 = 6

20.

Задание :Как можно вычислить
другим способом?
4· 3 - 2 · 3 = 12 - 6 =12

21.

(4 - 2) · 3 = 2 · 3 = 18
4· 3 - 2 · 3 = 12 - 6 =18
Умножение разности на число

22.

Распределительное свойство
умножения относительно
вычитания

23.

Распределительное свойство умножения
относительно сложения
Для того чтобы умножить сумму на число, можно
умножить на это число каждое слагаемое и сложить
полученные произведения.
(a + b)c = ac + bc
Распределительное свойство умножения
относительно вычитания
Для того чтобы умножить разность на число, можно
умножить на это число уменьшаемое и вычитаемое и
из первого произведения вычесть второе.
(a – b)c = ac – bc

24.

ac+bc = c (a+b)
ac - bc = c(a-b)
Это называется- выносить
общий множитель за скобку.

25.

Применяя распределительное свойство умножения
относительно сложения или вычитания к выражению
(a+ b) • с и (a - b) • c, мы получаем выражение, не
содержащее скобки. В этом случае говорят, что мы
раскрыли (опустили) скобки. Для применения
свойств не имеет значения, где записан множитель
"c" – перед скобками или после.
Раскроем скобки в выражениях:
2(t + 8) = 2t + 16
(3b - 5)4 = 4 • 3b - 4 • 5 = 12b - 20

26.

ЗАПОМНИТЕ!!!
Если перед буквой не записано число, то
подразумевается, что перед буквой стоит числовой
множитель 1.
t + 4t = (1 + 4)t = 5t
Вынесение общего множителя за скобки
Поменяем местами правую и левую часть равенства:
(a + b)с = ac + bc
Получим:
ac + bc = (a + b)с
В таких случаях говорят, что из "ac + bc" вынесен общий
множитель "с" за скобки.

27.

Примеры вынесения общего
множителя за скобки
73 • 8 + 7 • 8 = (73 + 7) • 8 = 80 • 8 = 640
7x - x - 6 = (7 - 1)x - 6 = 6x - 6 = 6(x - 1)

28.

Найдите значение выражения
наиболее удобным способом
а) 67 · 149 + 149 · 33 = 14900
б) 154 · 67 – 57 · 154 = 1540

29.

Вычислите с помощью
распределительного свойства
умножения:
102 ∙ 20 = (100 + 2)∙20 = 100 ∙ 20 + 2 ∙ 20 = 2000 + 40 = 2040
198 ∙ 15 = (200 – 2)∙15 = 200 ∙ 15 – 2 ∙ 15 = 3000 – 30 = 2970
90 ∙ 25 + 10 ∙ 25 = (90 + 10) ∙ 25 = 100 ∙ 25 = 2500
123 ∙ 27 – 23 ∙ 27 = (123 - 23) ∙ 27 = 100 ∙ 27 = 2700

30.

Физкультминутка
Вы, наверное, устали?
Ну, тогда все дружно встали.
Вверх ладошки! Хлоп! Хлоп!
По коленкам – шлёп, шлёп!
По плечам теперь похлопай!
По бокам себя пошлёпай!
Мы осанку исправляем
Спинки дружно прогибаем
Вправо, влево мы нагнулись,
До носочков дотянулись.
Плечи вверх, назад и вниз.
Улыбайся и садись.

31.

Задания в классе
№ 559(1 ст)
№ 560 (1ст)
№ 557

32.

Рассмотри задачу:
На столе лежат три коробки с карандашами. В первой х
карандашей. Во второй – в 2 раза больше, а в третьей в 5
раз больше, чем в первой. Сколько карандашей во второй и
третьей коробках.

33.

Представьте в виде произведения
выражения:
23а + 37а = (23 + 37)·а = 60 ∙ а = 60а
у + 26у = (1 + 26)·у = 27у
27р – 17р = (27 – 17)·р = 10р
32k – k = (32 – 1)·k = 31k

34.

Упростите, если возможно
выражения подчеркнув коэффициенты:
17m + 5m = 22m
6a – a = 5а
9c + 4c – 6c = 7c
5 + 12n – 2n = 5 + 10n
24b + 7a – 5a = 24b + 2а
y – 8 = невозможно

35.

Задания в классе
№ 562 (устно)
№ 563
№568
№573
№ 579

36.

Упростите выражение и
найдите его значение:
1)
2)
3)
4)
5)
3х + 8х
при х = 13
13у – 6у при у = 6
12k – k
при k = 5
28у – 18у + 6у
при у = 3
15х + 5х – 10
при х = 10
на «5» решаем все примеры,
на «4» первые 4 примера,
на «3» первые 3 примера.

37.

Проверка:
3х + 8х = (3 + 8)х = 11х
если х = 13, то 11 ∙ 13 = 143
13у – 6у = (13 – 6)у = 7у
если у = 6, то 7 ∙ 6 = 42
Так держать!
12k – k = (12 – 1)k = 11k
если k = 5, то 11 ∙ 5 = 55
28у – 18у + 6у = (28 – 18 + 6)у = 16у
если у = 3, то 16 ∙ 3 = 48
15х + 5х – 10 = (15 + 5)х – 10= 20х – 10
если х = 10, то 20 ∙ 10 – 10 = 190

38.

Итоги урока. Рефлексия
• Какую новую тему мы сегодня изучили?
• Какие свойства мы применяли при упрощении
выражений?
• Сможете вы сами находить и применять эти свойства
при решении примеров и уравнений?
• Что у вас не получилось? Что не понятно?
• Вам понравился урок?

39.

П. 14 №610 , №616,
№612, №614(а,б)

40.

Удачи на следующих уроках!