Похожие презентации:
Додавання і множення числових нерівностей (9 клас)
1.
15 вересняКласна робота
Додавання і множення
числових нерівностей
2.
Властивості числовихнерівностей
3.
Наслідки з властивостейчислових нерівностей
4.
Додавання числових нерівностейЯкщо додати дві правильні числові нерівності одного
знака:
5 7
+
4 0
то отримаємо правильну нерівність:
1 7
Властивість: Якщо почленно додати правильні
нерівності одного знака, залишивши їх спільний знак, то
одержимо правильну нерівність.
Якщо a > b і с > d, то a + с > b + d
Наприклад, якщо 18 > 10
– 9 > – 12,
18 + (–9) > 10 + (– 12);
9>–2
5.
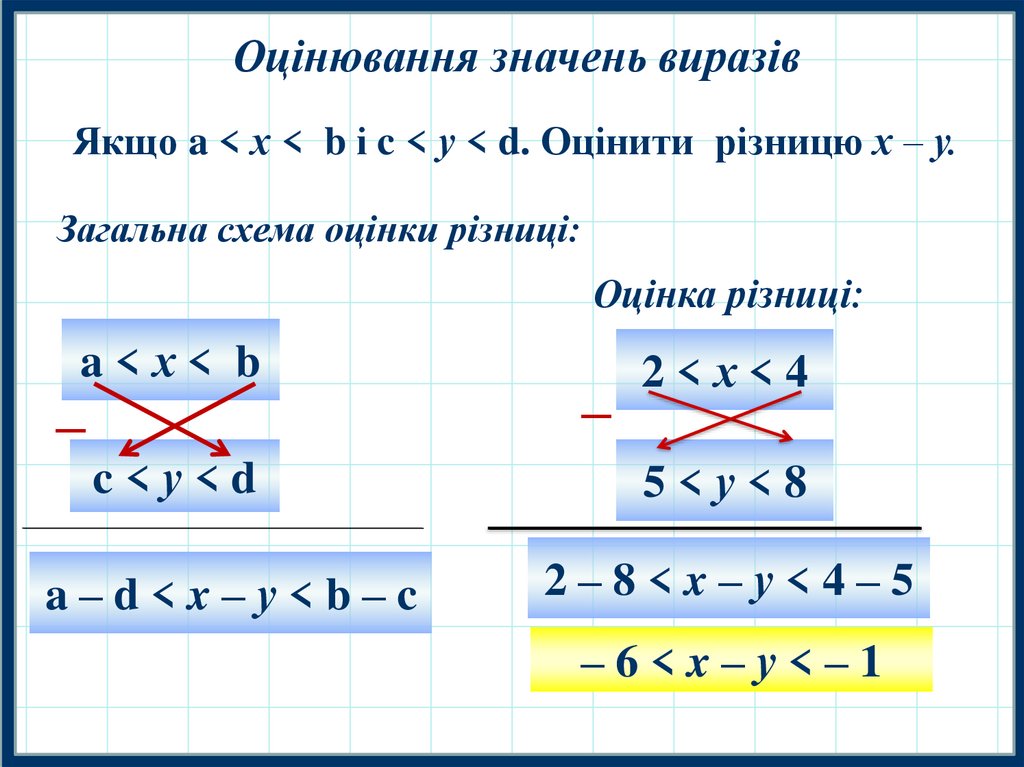
Оцінювання значень виразівЯкщо a < х < b і c < у < d. Оцінити суму х + у
Загальна схема оцінки
суми:
+
Якщо 2 < х < 4 і 5 < у < 8.
Оцінити суму х + у
Оцінка суми:
a<х< b
c<у<d
a+c<x+у<b+d
+
2<х<4
5<у<8
2+5<x+у<4+8
7 < x + у < 12
6.
Додавання числових нерівностейДодайте почленно нерівності:
1) -15 < –5 i 7 <10
-8 < 5
2) –55 > –78 i 71 > 36
16 > –42
3) –5,4 < 0,7 i 1,4 < 3,7
–4 < 4,4
4) 1,3 < 3,2 i –7 < 0
– 5,7 < 3,2
7.
Множення числових нерівностейЯкщо помножити дві
правильні нерівності одного знака:
5 7
×
2 3
то отримаємо правильну нерівність:
10<21
Властивість: Якщо почленно перемножити правильні
нерівності одного знака, ліві і праві частини яких – додатні
числа, залишивши їх спільний знак, то одержимо правильну
нерівність.
Якщо a > b і с > d, і a,с,b,d – додатні, то aс > bd
Наприклад, якщо 8 > 3
9>2
8 9 > 3 2;
72 > 6.
8.
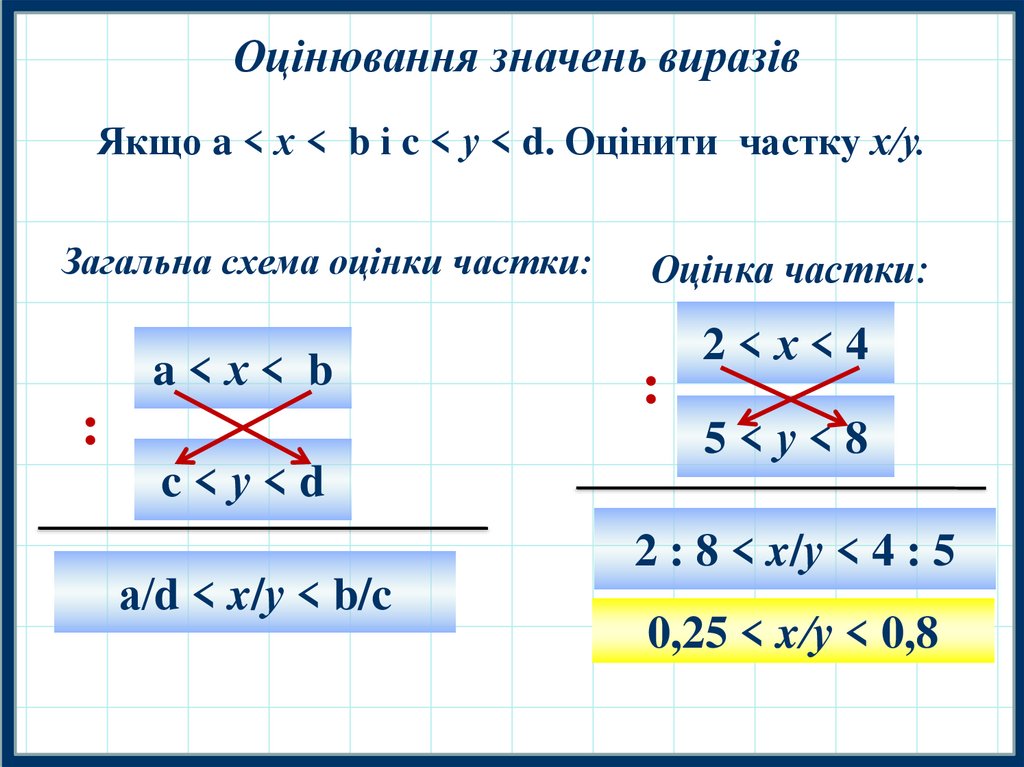
Оцінювання значень виразівЯкщо a < х < b і c < у < d. Оцінити добуток ху
Загальна схема оцінки добутку
Оцінка добутку:
×
a<х< b
2<х<4
c<у<d
×
аc < xу < bd
2 5 < xу < 4 8
5<у<8
10 < xу < 32
9.
Множення числових нерівностейПеремножте почленно нерівності:
1) 5 < 6 i 7 < 11
35 < 66
2) 50 > 25 i 10 > 4
500 > 100
3) 0,4 < 0,7 i 3 < 7
1,2 < 4,9
4) 1,3 < 2,2 i 0, 2 < 0,3
0,26 < 0,66
10.
Піднесення до степеня числових нерівностейЯкщо a > b і a, b, – додатні, то an > bn
Наприклад, якщо 5 > 3,
то 52 > 32; 25 > 9,
або 54 > 34; 625 > 81.
Задача: порівняйте площі квадратів із
сторонами 2,6 см і 5,4 см.
Розв’язання:
S = a2
Оскільки 2,6 см < 5,4 см, то і
2,62 см2 < 5,42 см2 або
6,76 см2 < 29,16 см2
11.
Розв’язування вправ:Оцініть периметр і площу квадрата зі
стороною а, якщо відомо, що 1,3 < а < 1,5.
1) Р = 4а
1,3 4 < 4а < 1,5 4; 5,2 < Р < 6
2) S = a2
1,32 < a2 < 1,52; 1,69 < S < 2,25
12.
Віднімання числових нерівностейВіднімання числових нерівностей одного знака
заміняється додаванням протилежного значення:
a – b = a + (– b)
Нехай маємо дві нерівності одного знака:18 > 10 і 9 > 2.
Обидві частині другої нерівності
9 2
помножимо на (– 1), отримаємо:
А тепер додаємо нерівності:
Отже отримали:
18>
















 Математика
Математика








