Похожие презентации:
Числові ряди
1. Глава 9. РЯДИ
§1. ЧИСЛОВІ РЯДИ1.1. Основні поняття та означення.
Геометрична прогресія. Гармонічний ряд
un u1, u2 , u3 , , un ,
Озн. Рядом називають вираз
u1 u2 u3 un un
n 1
(1)
2.
S1 u1S2 u1 u2
S3 u1 u2 u3
Sn u1 u2 u3 un
Озн. Число un називається n-м членом ряду (1).
Озн. Число Sn називається n-ю частинною сумою ряду (1).
Озн. Якщо послідовність частинних сум {Sn} збіжна і
lim Sn S,
n
то число S називається сумою ряду (1), а ряд називається
збіжним.
S u1 u2 u3 un un
n 1
Озн. Якщо послідовність частинних сум {Sn} скінченної
границі не має, то ряд (1) називається розбіжним.
3.
Прикладиа)
1 1 1 1 1n
n 1
Sn 1 1 1 1 n
lim Sn lim n .
n
n
Ряд розбіжний.
4.
Прикладиб) 1 1 1 1 1
n 1
1
n 1
n 1
S1 1
S3 1
S5 1
S2 n 1 1
S2 0
S4 0
S6 0
S2n 0
послідовність {Sn} границі не має, тому ряд б) розбіжний.
5.
Прикладив)
1
1
1
1
1 2 2 3
n (n 1)
n 1 n ( n 1)
1
1
1
1
Sn
1 2 2 3 3 4
n (n 1)
1
1
1
1 1 1 1 1
1
1
.
n 1
2 2 3 3 4
n (n 1)
1
1
lim Sn lim 1
n
n
n 1
S 1.
Оскільки S = 1, то ряд в) збіжний і сума його дорівнює 1.
6.
Прикладид)
1
1 1 1
1
1
2 3 4
n
n 1 n
Цей ряд називається гармонічним.
n
1
1 e
n
1
n ln 1 1
n
n 1 1
ln
n n
1
n 1
ln
n
n
1
ln n 1 ln n
n
7.
Прикладид)
1
1 1 1
1
1
2 3 4
n
n 1 n
Цей ряд називається гармонічним.
1
ln n 1 ln n
n
1 ln 2 ln 1
1
ln 3 ln 2
2
1
ln 4 ln 3
3
1
ln 5 ln 4
4
1
ln n 1 ln n
n
8.
Прикладид)
1
1 1 1
1
1
2 3 4
n
n 1 n
Цей ряд називається гармонічним.
Sn ln n 1
lim ln n 1
n
lim Sn
n
Отже, гармонічний ряд розбіжний.
9.
1.2. Найпростіші властивості числових рядів1°. Якщо ряд
u
n 1
n
збіжний і має суму S, то ряд
Cu
n 1
n
також збіжний і сума його дорівнює CS (С = const).
2°. Збіжні ряди можна почленно додавати та віднімати.
3°. На збіжність ряду не впливає відкидання або
приєднання до нього скінченної кількості членів.
.
10.
rn un 1 un 2 un 3u
k n 1
k
Величину rn називають n-м залишком ряду (1)
Якщо ряд збіжний
lim Sn S,
n
rn S Sn ,
lim rn 0.
n
11.
4°. Ряд (1) збіжний (розбіжний) тоді і тільки тоді,коли збіжний (розбіжний) довільний його залишок.
5°. (Необхідна
умова збіжності ряду.)
Якщо ряд
un збіжний, то lim un 0.
n
n 1
6°. (Достатня умова розбіжності
ряду.)
un розбіжний.
Якщо lim un 0, то ряд
n
n 1
12.
ПрикладиДослідити на збіжність ряди:
1
а)
n
n 1
1
un
n
1
lim un lim
0.
n
n
n
1
1
1
1
1
1
1
1
Sn
n
n
n
n
1
2
3
n
1
n
n.
n
Sn n
lim Sn .
n
Ряд розбіжний.
13.
ПрикладиДослідити на збіжність ряди:
2n 1
б)
n 1 n 2
2n 1
un
n 2
2n 1
lim un lim
2 0.
n
n n 2
Ряд розбіжний.
14.
ПрикладиДослідити на збіжність ряди:
1
в) n
n 1 2
1
Геометрична прогресія q .
2
| q | 1
Ряд збіжний.
| q | 1
— ряд збіжний
| q | 1
— ряд розбіжний
15.
1.3. Знакододатні ряди.Достатні ознаки збіжності
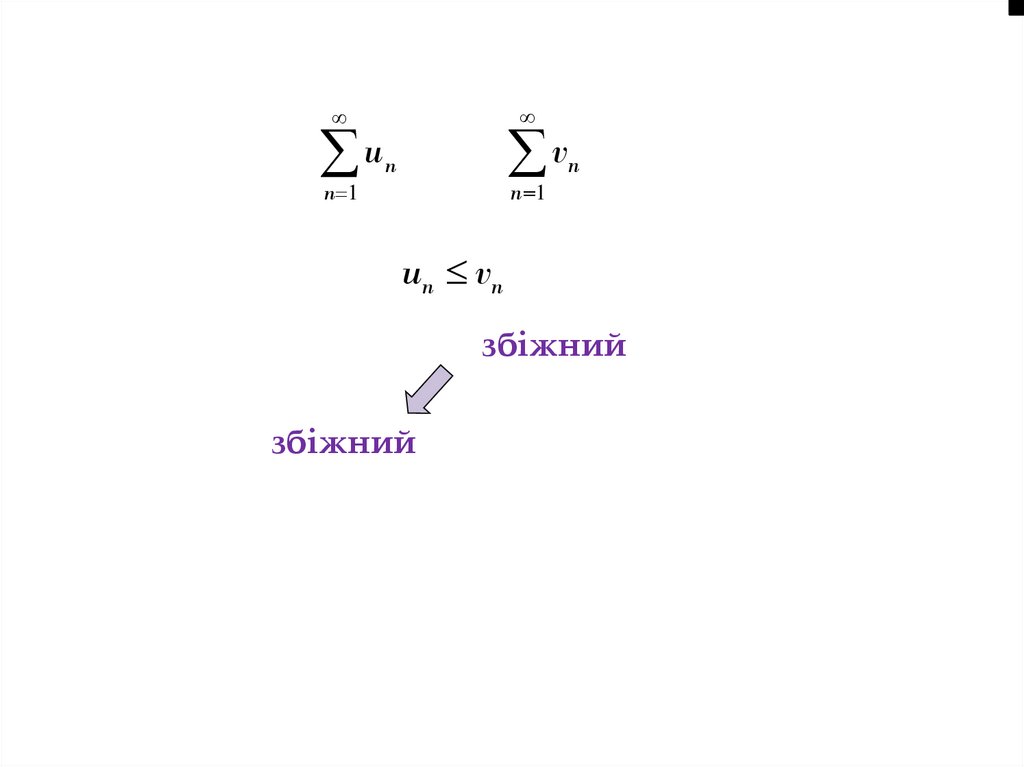
Теорема 1 (ознаки порівняння).
Нехай задано два ряди з невід'ємними членами
u ,
n 1
n
(2)
v ,
n 1
n
(3)
і для всіх n виконується нерівність
un vn .
Тоді, якщо ряд (3) збіжний, то збіжний і ряд (2).
Якщо ряд (2) розбіжний, то розбіжний і ряд (3).
(4)
16.
un 1
v
n
n 1
n
un vn
збіжний
збіжний
17.
un 1
v
n
n 1
n
un vn
розбіжний
розбіжний
18.
1.3. Знакододатні ряди.Достатні ознаки збіжності
Теорема 1 (ознаки порівняння).
Нехай задано два ряди з невід'ємними членами
u ,
n 1
n
(2)
v ,
n 1
n
(3)
і для всіх n виконується нерівність
un vn .
Тоді, якщо ряд (3) збіжний, то збіжний і ряд (2).
Якщо ряд (2) розбіжний, то розбіжний і ряд (3).
(4)
19.
aqn 1
n 1
1
n
n 1
збіжний при | q | 1
розбіжний при | q | 1
1
розбіжний при 1
збіжний при
20.
ПрикладиДослідити на збіжність ряди:
1
а)
n
n
3
n 1
1
un
n 3n
1
vn n
3
1
1
n
n
n 3
3
1
n
3
n 1
геометрична прогресія
(ряд збіжний)
1
q 1
3
Ряд збіжний.
21.
ПрикладиДослідити на збіжність ряди:
1
б)
n 1 ln( n 1)
1
un
ln( n 1)
1
1
ln( n 1) n 1
1
vn
n 1
1
n 1 n 1
гармонічний ряд (α = 1)
(ряд розбіжний)
Ряд розбіжний.
22.
Теорема 2 (гранична ознака порівняння).Якщо задано два ряди з додатними членами
u ,
n 1
(5)
n
v ,
n 1
(6)
n
причому існує скінченна, відмінна від нуля границя
un
lim
a
n v
n
a 0, a ,
то ряди або одночасно збіжні, або одночасно розбіжні.
23.
ПрикладиДослідити на збіжність ряди:
tg
3n
n 1
а)
un tg
3n
1
vn
гармонічний ряд (α = 1)
n
tg
un
3
n
lim
lim
0.
n v
n
1
3
n
n
(ряд розбіжний)
Ряд розбіжний.
24.
ПрикладиДослідити на збіжність ряди:
2n 1
б)
3
n
n 1
2n 1
un
n3
1
vn 2
n
Узагальнений гармонічний
ряд (α = 2)
(ряд збіжний)
un
2n 1 1
lim
lim
: 2 2 0.
3
n v
n
n
n
n
Ряд збіжний.
25.
Теорема 3 (ознака Д'Аламбера).Якщо для ряду з додатними членами
u
n 1
існує границя
n
un 1
lim
l, то
n u
n
1) ряд збіжний при l 1;
2) ряд розбіжний при l 1.
(8)
26.
ПрикладиДослідити на збіжність ряди:
а)
n2
n
2
n 1
n2
n 1
un 1
un n
2n 1
2
2
2
n
1
n 1
un 1
n 1 2
1
.
lim
lim
lim
2
n 1
2
n
n u
n
2
2n
2
n
n
2
Ряд збіжний.
27.
ПрикладиДослідити на збіжність ряди:
б)
n!
n
2
n 1
n!
un n
2
un 1
n 1 !
2n 1
n 1
un 1
n 1 ! 2n
.
lim
lim
lim
n
1
n
2
n u
n 2
n
!
n
Ряд розбіжний.
28.
ПрикладиДослідити на збіжність ряди:
в)
nn
n 1 n!
n 1
n 1
n
un 1
un
n 1 !
n!
n
n 1
n 1
un 1
n 1
n!
lim
lim
lim
n
n
n
n u
n
n
n
n
1
!
n
n
n
1
lim 1
n
n
e 1.
Ряд розбіжний.
29.
Теорема 4 (ознака Коші).Якщо для ряду (8) з додатними членами існує границя
lim n un l,
n
1) ряд збіжний при l 1;
2) ряд розбіжний при l 1.
то
30.
ПрикладиДослідити на збіжність ряди:
а)
4n
n 1 n 1
n
4n
un
n 1
n
n
4
n
4
n
4 1.
lim
lim un lim n
n
n
n
n 1
n 1
n
Ряд розбіжний.
31.
ПрикладиДослідити на збіжність ряди:
б) sin
3n
n 1
n
un sin
3n
n
n
0 1.
lim un lim sin lim sin
n
n
n
3n
3n
n
n
Ряд збіжний.
32.
Теорема 5 (інтегральна ознака Коші).Нехай задано ряд
f (n)
n 1
члени якого є значеннями неперервної, додатної і
монотонно спадної функції f(x) на проміжку [ 1; +∞).
Тоді ряд (12) збіжний, якщо збіжний невласний
інтеграл
f ( x)dx,
1
і розбіжний, якщо цей інтеграл розбіжний.
(12)
33.
ПрикладиДослідити на збіжність ряди:
2n
2
n
3
n 1
а)
2x
f ( x) 2
x 3
2
x 1;
x 2;
b
2x
2
f ( x)dx 2
dx lim ln( x 3) .
2
b
x 3
2
Ряд розбіжний.
34.
1.4. Ряди, в яких знаки членів строгочергуються. Ознака Лейбніца
u1 u2 u3 u4 ( 1)n 1 un
(15)
un 0, n 1, 2, ...
Теорема 1 (ознака Лейбніца).
Ряд (15) збіжний, якщо
1)
un 1 un , n 1, 2, ...
(16)
2)
lim un 0.
(17)
n
При цьому сума ряду додатна і не перевищує першого
його члена.
35.
1.5. Знакозмінні ряди. Абсолютна і умовназбіжності
u1 u2 u3 un
(19)
u1 u2 u3 un
(20)
Теорема.
Якщо ряд (20) збіжний, то збіжний і ряд (19).
36.
ПрикладиДослідити на збіжність ряди:
sin n
а)
3
n
n 1
sin n
3
n
n 1
R
sin n
un
n3
1
vn 3
n
un vn
Узагальнений гармонічний ряд (α = 3)
1
vn 3
(ряд збіжний)
n 1
n 1 n
sin n
un
(ряд збіжний)
3
n
n 1
n 1
sin n
3
Ряд збіжний.
n
n 1
37.
u1 u2 u3 un(19)
u1 u2 u3 un
(20)
Знакозмінний ряд (19) називають абсолютно збіжним,
якщо ряд (20), утворений з модулів його членів, є збіжним.
Якщо ж ряд (19) збіжний, а ряд (20), утворений з модулів
його членів, розбіжний, то ряд (19) називають умовно
збіжним.
sin n
3
n
n 1
( 1)n
n
n 1
Ряд абсолютно збіжний.
Ряд умовно збіжний.
38.
ПрикладиДослідити на збіжність ряди:
sin n
а)
3
n
n 1
sin n
3
n
n 1
R
sin n
un
n3
1
vn 3
n
un vn
Узагальнений гармонічний ряд (α = 3)
1
vn 3
(ряд збіжний)
n 1
n 1 n
sin n
un
(ряд збіжний)
3
n
n 1
n 1
sin n
3
Ряд абсолютно збіжний.
n
n 1
39.
Зазначимо, що розмежування рядів на абсолютно іумовно збіжні є досить істотним. Справа в тому, що
абсолютно збіжні ряди мають цілу низку важливих
властивостей скінченних сум, тоді як умовно збіжні ряди
таких властивостей не мають.
Наприклад, абсолютно збіжні мають переставну
властивість: будь-який ряд, утворений за допомогою
перестановки членів абсолютно збіжного ряду, також
абсолютно збіжний і має ту саму суму, що і заданий ряд.
Умовно збіжні ряди переставної властивості не мають,
тому що від перестановки їхніх членів може змінитися
сума ряду і навіть утворитись розбіжний ряд.
40.
§2. СТЕПЕНЕВІ РЯДИ2.1. Функціональні ряди. Поняття
рівномірної збіжності. Ознака Вейерштрасса
u1 ( x) u2 ( x) un ( x) un ( x)
(24)
n 1
x0 D
u1 ( x0 ) u2 ( x0 ) un ( x0 ) un ( x0 )
n 1
(25)
41.
Множина всіх точок збіжності функціонального рядуназивається областю його збіжності.
Sn ( x) u1 ( x) u2 ( x) un ( x)
lim Sn ( x) S( x)
n
S( x) u1 ( x) u2 ( x) un ( x) ...
rn ( x) un 1 ( x) un 2 ( x)
lim rn ( x) 0
n
42.
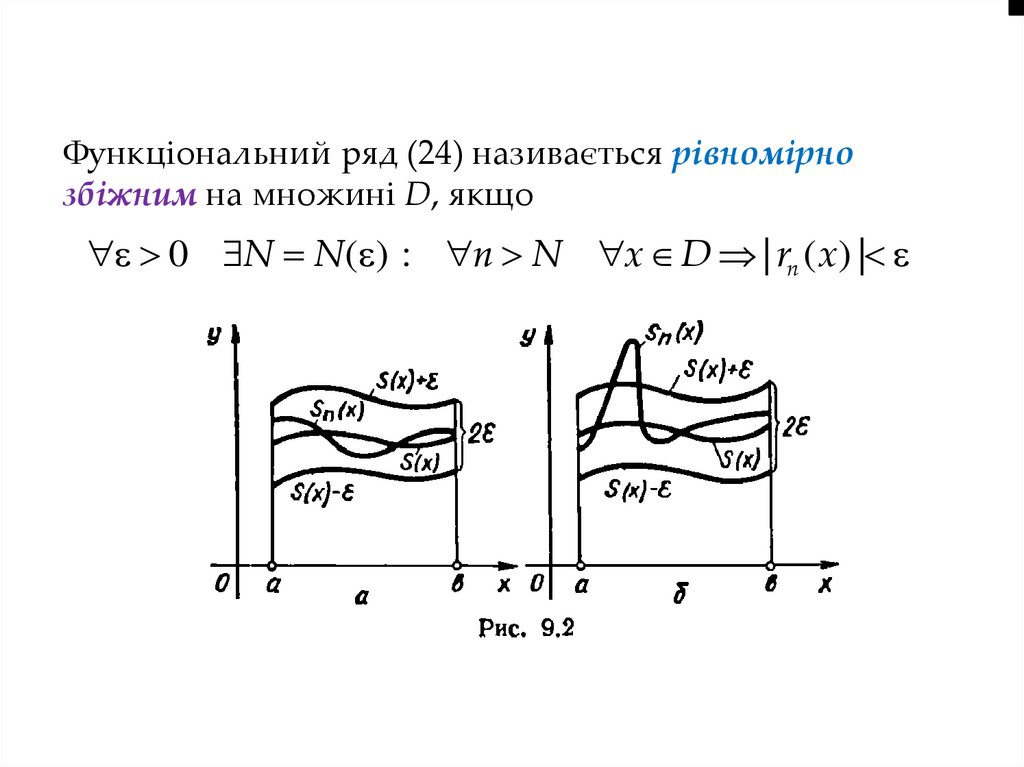
Функціональний ряд (24) називається рівномірнозбіжним на множині D, якщо
0 N N( ) : n N x D | rn ( x) |
43.
Властивості для рівномірно збіжних рядів• 1°. Сума членів рівномірно збіжного на деякому
проміжку ряду неперервних функцій є функція,
неперервна на цьому проміжку.
• 2°. Якщо на відрізку [a; b] функціональний ряд (24)
рівномірно збіжний і члени ряду неперервні на
[a; b], то його можна почленно інтегрувати
в межах ( ; ), де ( , ) [а; b]:
un ( x) dx un ( x)dx
n 1
n 1
44.
Властивості для рівномірно збіжних рядів• 3°. Якщо функціональний ряд (24) збіжний на [a; b],
а його члени мають неперервні похідні u n(x),
x [а; b], n = 1, 2, … , причому ряд
u ( x)
n 1
n
рівномірно збіжний на [a; b], то заданий ряд можна
почленно диференціювати, тобто
un ( x) u n ( x)
n 1
n 1
45.
Теорема (ознака Вейєрштрасса).Функціональний ряд (24) абсолютно і рівномірно
збіжний на відрізку [а; b], якщо існує знакододатний
збіжний числовий ряд
a
n 1
n
такий, що
un ( x) an x [a, b], n 1, 2, ...
46.
Приклади1. Знайти область збіжності функціонального ряду:
1
n
x
n 1
1
1 1
1
2 ... n ...
n
x x
x
n 1 x
1
q
x
1
| q |
x
x ( ; 1) (1; )
1
x ( ;0) (0; )
x 1
– область збіжності ряду.
47.
Приклади2. Дослідити на рівномірну збіжність ряд :
sin nx
n!
n 1
x , n N
sin nx sin x sin 2 x
sin nx
...
...
n!
1!
2!
n!
n 1
sin nx
1
n!
n!
1
n 1 n!
– ряд збіжний
тому заданий функціональний ряд абсолютно і
рівномірно збіжний на всій числовій осі.
48.
2.2. Поняття степеневого ряду.Теорема Абеля. Інтервал та радіус збіжності
степеневого ряду
Степеневим рядом, називається функціональний ряд
вигляду
a0 a1x a2 x 2 an x n
an x n
(28)
n 0
a0 a1 x x0 a2 x x0 an x x0
n
2
an x x0
n 0
n
(29)
49.
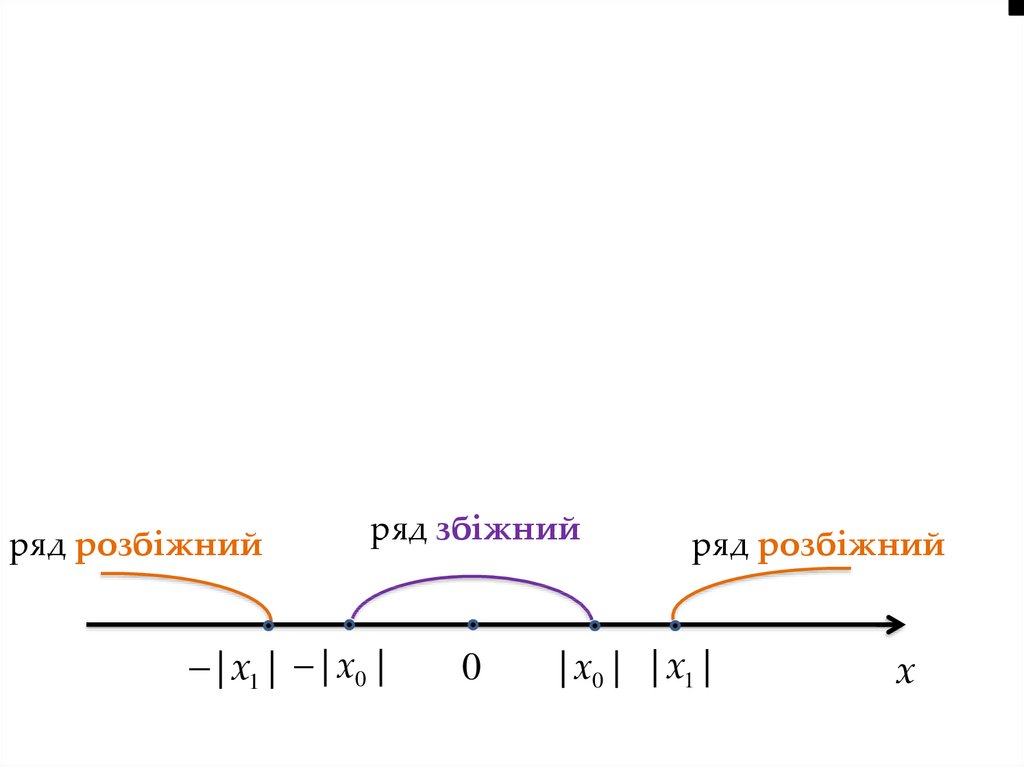
Теорема Абеля.Якщо степеневий ряд (28) збіжний при х = х0 0,
то він абсолютно збіжний для всіх значень х,
що задовольняють нерівність |x| < |x0|
Якщо при х = х1 ряд розбіжний, то він розбіжний
всюди, де |x| > |x1|.
ряд розбіжний
ряд збіжний
| x1 | | x0 |
0
ряд розбіжний
| x0 | | x1 |
x
50.
ряд розбіжнийряд збіжний
| x1 | | x0 |
0
ряд розбіжний
| x0 | | x1 |
x
51.
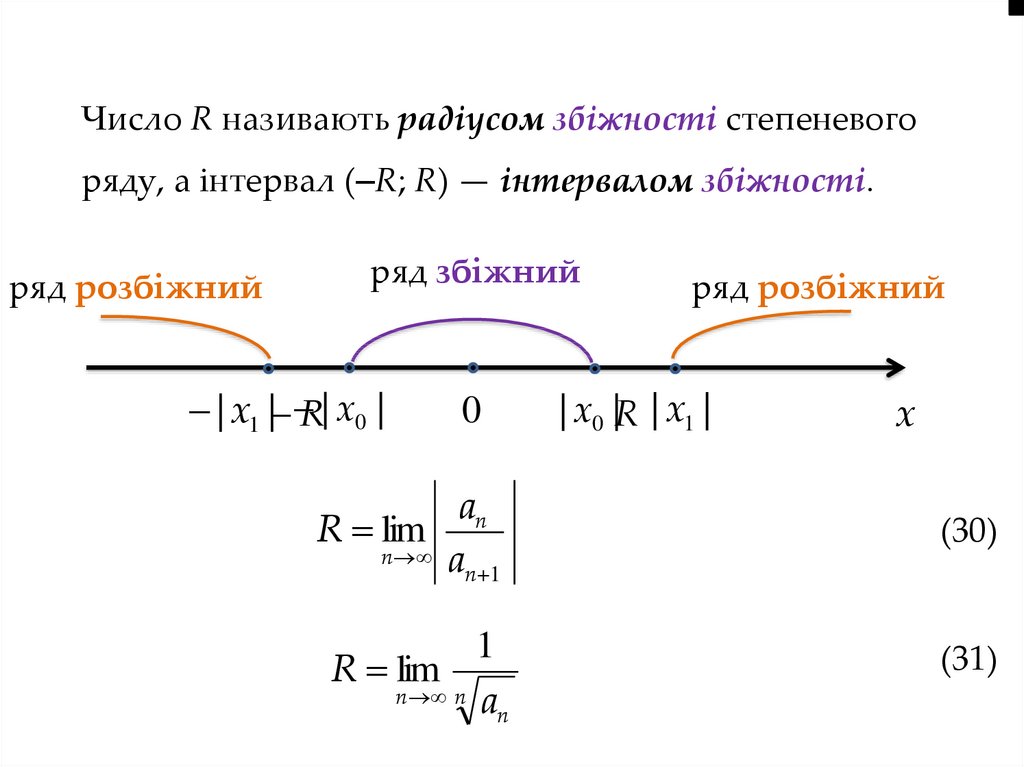
Число R називають радіусом збіжності степеневогоряду, а інтервал (–R; R) — інтервалом збіжності.
ряд розбіжний
ряд збіжний
| x1 | R| x0 |
0
an
R lim
n a
n 1
1
R lim
n n a
n
ряд розбіжний
| x0 |R | x1 |
x
(30)
(31)
52.
Приклади1. Знайти область збіжності ряду:
1 n
x
n 0 n!
( n 1)!
an
lim ( n 1) .
R lim
lim
n
n a
n
n!
n 1
Даний ряд абсолютно збіжний на всій числовій осі.
53.
Приклади2. Знайти область збіжності ряду:
n
nx
n 0
an
nn
R lim
lim
0.
n a
n ( n 1) n 1
n 1
Даний ряд збіжний лише в точці х = 0.
54.
Приклади3. Знайти область збіжності ряду:
xn
n 0 2n 1
2n 3
an
R lim
lim
n
n a
2n 1
n 1
1.
Отже, (–1; 1) інтервал збіжності даного ряду.
х = –1
1 n
1 1 1
– збіжний за ознакою
1
...
Лейбніца.
3 5 7
n 0 2n 1
х=1
– розбіжний за
1
1 1 1
1 ... ознакою порівняння.
3 5 7
n 0 2n 1
Областю збіжності даного ряду є проміжок [–1; 1).
55.
Приклади4. Знайти область збіжності ряду:
x 3 n
n 1
n2
2
an
n 1
R lim
lim
1.
2
n a
n
n
n 1
| x 3 | 1
1 3 x 1 3
1 x 3 1
4 x 2
R 1.
Отже, (–4; –2) інтервал збіжності даного ряду.
56.
х = –41
n 1
n
n
2
– збіжний за ознакою Лейбніца.
х = –2
1
2
n
n 1
– збіжний, (узагальнений
гармонічний ряд при α = 2).
Областю збіжності даного ряду є відрізок [–4; –2].
57.
2.3. Властивості степеневих рядів1. Степеневий ряд
n
a
x
n
n 0
абсолютно і рівномірно збіжний на будь-якому
відрізку [ ; ], який цілком міститься в інтервалі
збіжності ( R; R).
2. Сума степеневого ряду (28) неперервна всередині
його інтервалу збіжності.
58.
3. Якщо межі інтегрування та лежать всерединіінтервалу збіжності ( R; R) ряду (24), то на відрізку
[ ; ] цей ряд можна почленно інтегрувати.
4. Якщо ряд (28) має інтервал збіжності ( R; R), то ряд
утворений диференціюванням ряду (28), має той
самий інтервал збіжності ( R; R);
при цьому, якщо S(х) — сума ряду (28), то
S ( x) nan x n 1 ,
n 0
x ( R; R).
59.
2.4. Ряд Тейлораn
2
n
a
x
a
a
x
a
x
a
x
S(x )
n
0
1
2
n
n 0
R x R
a x x
n 0
n
n
0
a0 a1 x x0 a2 x x0 an x x0
2
n
R x x0 R
x0 R x x0 R
f ( x) an x x0
n 0
n
(32)
60.
f (x) a0 a1 x x0 a2 x x0 2 an x x0 nx x0
f ( x0 ) a0
a0 f ( x0 )
f (x) a1 2 1a2 x x0 3a3 x x0 2 nan x x0 n 1
x x0
f ( x0 ) a1
a1 f ( x0 )
1
2
f (x) 2 1a2 3 2a3 x x0 4 3a4 x x0
n(n 1)an x x0
n 2
x x0
f ( x0 ) 1 2a2
1
a2
f ( x0 )
1 2
61.
f (x) 3 2 1a3 4 3 2a4 x x0 1 5 4 3a5 x x0 2n(n 1)( n 2)an x x0
n 3
x x0
1
a3 f ( x0 )
3!
f ( x0 ) 1 2 3a3
f IV ( x) 4 3 2a4 5 4 3 2a5 x x0 1
n(n 1)( n 2)( n 3)an x x0
n 4
x x0
f ( x0 ) 4! a4
IV
1 IV
a4 f ( x0 )
4!
62.
1a1 f ( x0 )
1!
a0 f ( x0 )
1 IV
a4 f ( x0 )
4!
.......
1
a2 f ( x0 )
2!
1
a3 f ( x0 )
3!
1 (n)
an f ( x0 )
n!
.......
f ( x0 )
f ( x0 )
x x0
x x0 2
f (x) f ( x0 )
1!
2!
f
( n)
( x0 )
x x0 n
n!
n 0
f ( n) ( x0 )
n
x x0
n!
Ряд (33) називається рядом Тейлора функції f(x).
(33)
63.
Теорема 1.Якщо функцію f(x) в інтервалі (x0 R; x0 + R) можна
розкласти в степеневий ряд, то цей ряд єдиний
і є рядом Тейлора даної функції.
Теорема 2.
Для того щоб ряд Тейлора (33) збігався до функції f(x)
в інтервалі (x0 R; x0 + R) необхідно і достатньо, щоб
в цьому інтервалі функція мала похідні всіх порядків
і залишковий член її формули Тейлора прямував
до нуля при n для всіх х з цього інтервалу:
lim Rn ( x) 0
n
x x0 R; x0 R
(34)
64.
lim Rn ( x) 0n
x x0 R; x0 R
(34)
f ( x0 )
f ( x0 )
x x0
x x0 2
f (x) f ( x0 )
1!
2!
(35)
f ( n) ( x0 )
x x0 n Rn ( x)
n!
f ( n 1) x ( x x0 )
Rn ( x)
( x x0 )n 1,
(n 1)!
0 1
(36)
— залишковий член формули Тейлора у формі Лагранжа
65.
f (x) Sn ( x) Rn ( x)(37)
lim Sn ( x) f (x)
n
Теорема 3.
Якщо функція f(x) в інтервалі (x0 R; x0 + R) має
похідні всіх порядків та існує число М > 0 таке, що
f ( n ) ( x ) M,
x x0 R; x0 R , n 0, 1, 2, ...,
то функцію f(x) можна розкласти в ряд Тейлора.
(38)
66.
2.5. Розкладання елементарних функційв ряд Маклорена
Рядом Маклорена функції f(x) називають степеневий ряд
по степенях х, який можна дістати з ряду (38) при х0 = 0:
f (x)
n 0
f ( n) (0) n
x
n!
(41)
Правило розкладання функції f(x) в ряд Маклорена:
а) знайти похідні;
б) обчислити значення похідних в точці х = 0;
в) записати ряд Маклорена (41) для даної функції і знайти
інтервал його збіжності;
г) визначити інтервал ( R; R), в якому залишковий член
формули Маклорена прямує до нуля (n ).
67.
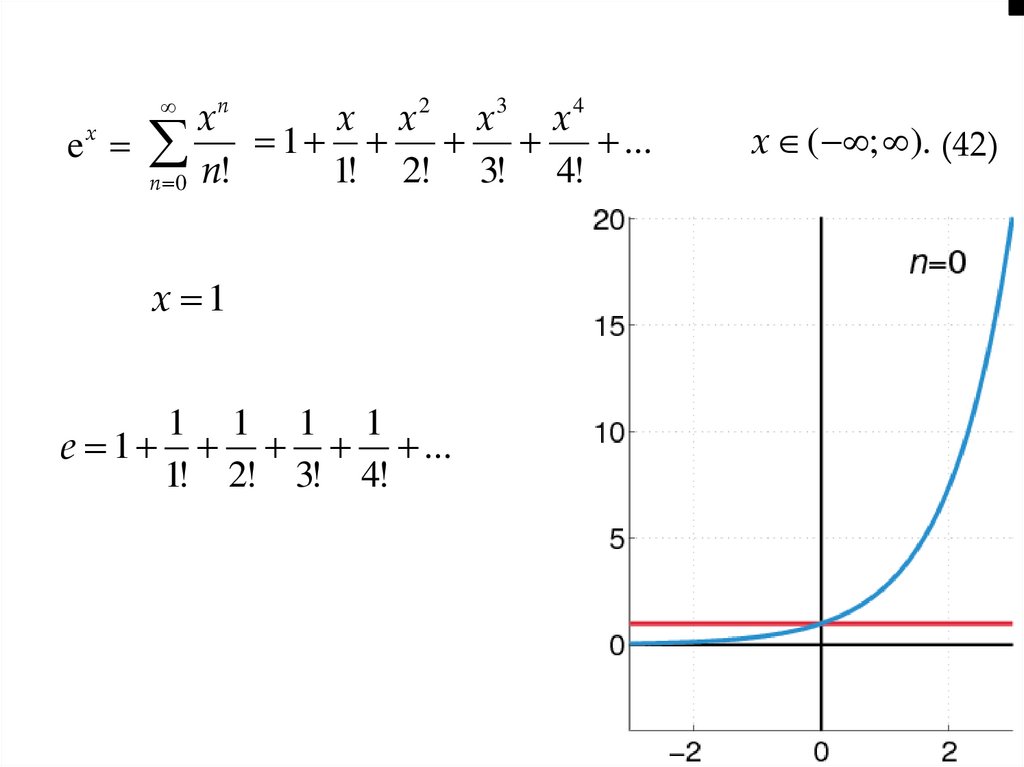
n2
3
4
x
x
x
x
x
1 ...
ex
1! 2! 3! 4!
n 0 n!
x 1
1 1 1 1
e 1 ...
1! 2! 3! 4!
x ( ; ). (42)
68.
x 3 x5 x 7( 1)n x2n 1
x ... x ( ; ). (43)
sin x
3! 5! 7!
n 0 ( 2n 1)!
( 1)n x2 n
x 2 x 4 x6
1 ...
cos x
2! 4! 6!
(2n)!
n 0
x ( ; ). (44)
69.
m ( ; )1 x
m
m(m 1)...( m n 1) xn
n!
n 0
x ( 1; 1)
(45)
mx m(m 1) x2 m(m 1)( m 2) x3
1
...
1!
2!
3!
m 2
m 3
m 1
m 1
1 x 2
1 x 3
1 2x x2
1 3x 3x2 x3
1
1
1 x x2 x3 ...
1 x
1 x
1
1
1 x x2 x3 ...
1 x
1 x
(46)
70.
x2 x3 x 4( 1) n 1 x n
x ...
ln 1 x
2
3 4
n
n 0
x ( 1; 1] (47)
x 3 x5 x 7
( 1)n x2 n 1
arctg x
x ...
3 5 7
2n 1
n 0
x [ 1; 1] (48)
1 3
1 3 5
1 3 5 7
x
x
x ...
arcsin x x
2 3
2 4 5
2 4 6 7
x [ 1; 1]
x 1
1 3 5 7
1
1 3
1 3 5
1
...
2
2 3 2 4 5 2 4 6 7 2 4 6 8 9
71.
ПрикладиЗнайти три перших (відмінних від нуля) члени розкладу
в ряд розв'язку рівняння
y xy y
y(0) 0, y (0) 1
y (0)
y (0) 2 y (0) 3
y ( n) (0) n
y ( x ) y ( 0)
x
x
x ...
x ...
1!
2!
3!
n!
y (0) xy (0) y(0) 0 1 0 0
y xy y y xy y 2y xy
y
IV
2y y xy 3y xy
y V 3y y xy IV 4 y xy IV
y (0) 2
y IV (0) 0
y V (0) 8
1
0 2 2 3 0 4 8 5
1 3 1 5
y( x) 0 x x x x x x x x .
1!
2!
3!
4!
5!
3
15
72.
§3. РЯДИ ФУР’Є3.1. Гармонічні коливання
Просте гармонічне коливання задається функцією
x(t ) a sin t 0 ,
t 0
(69)
a амплітуда коливання;
циклічна частота;
0 початкова фаза.
2
T
основний період функції.
Озн. Функція (69) (та її графік) називається простою
гармонікою.
73.
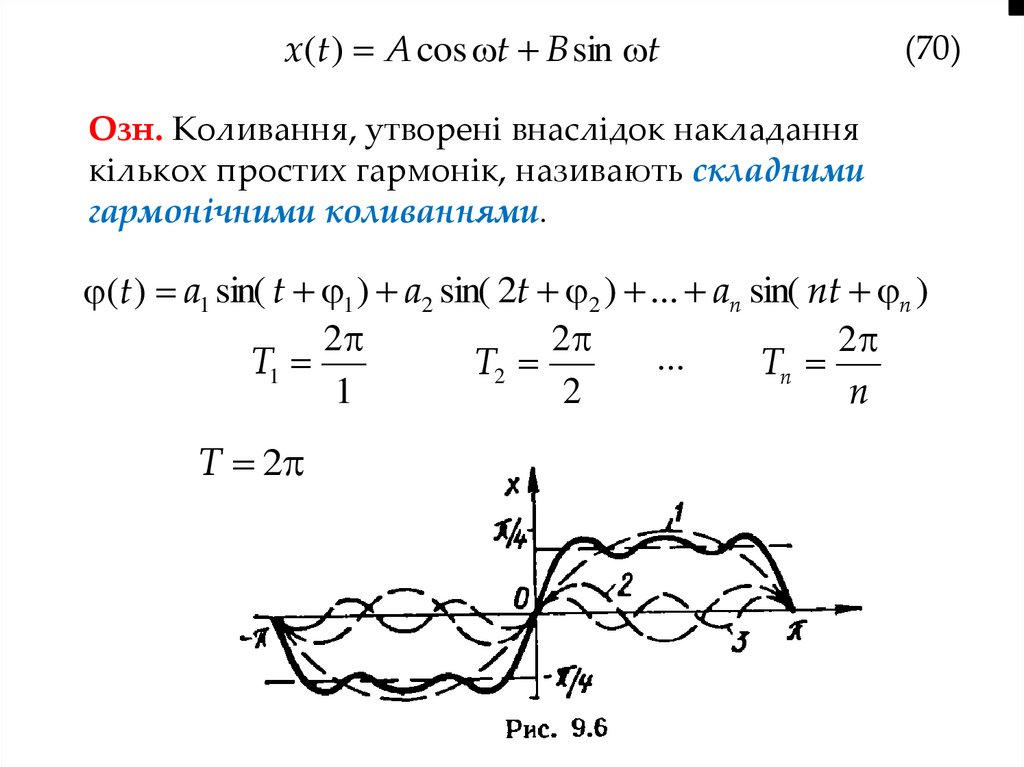
x(t ) A cos t B sin t(70)
Озн. Коливання, утворені внаслідок накладання
кількох простих гармонік, називають складними
гармонічними коливаннями.
(t ) a1 sin( t 1 ) a2 sin( 2t 2 ) ... an sin( nt n )
2
2
2
...
T1
T2
Tn
1
2
n
T 2
74.
3.2. Тригонометричний ряд Фур’є.Коефіцієнти Фур’є
Ряд виду
a0
a1 cos x b1 sin x a2 cos 2 x b2 sin 2 x ...
2
(71)
a0
an cos nx bn sin nx
an cos nx bn sin nx ...
2 n 1
називається тригонометричним рядом.
Дійсні числа a0, an, bn (n = 1, 2, …)— його коефіцієнтами.
75.
Припустимо, що ряд (71) на відрізку [– ; ] рівномірнозбіжний до функції f(х):
a0
an cos nx bn sin nx
f (x)
2 n 1
(72)
1
a0 f ( x)dx
(73)
1
an f ( x) cos nxdx, n 1, 2, ...
1
bn f ( x) sin nxdx, n 1, 2, ...
a0
an cos nx bn sin nx
f (x) ~
2 n 1
(75)
(76)
(77)
76.
a0an cos nx bn sin nx
f (x) ~
2 n 1
(77)
Теорема 1.
Якщо функцію f(x) можна подати на відрізку [– ; ]
у вигляді рівномірно збіжного на цьому відрізку
тригонометричного ряду (77) — то цей тригонометричний
ряд єдиний і є рядом Фур'є для функції f(x).
77.
Теорема 2.(достатня умова подання функції через її ряд Фур'є).
Нехай періодична функція f(x) з періодом 2 є кусковомонотонна і обмежена на відрізку [– ; ].
Тоді ряд Фур'є функції f(x) є збіжним на всій числовій осі.
Сума S(x) знайденого ряду дорівнює значенню функції f(x)
в усіх точках неперервності функції f(x);
якщо х0 — точка розриву функції f(x), то
f ( x0 0) f ( x0 0)
S( x0 )
;
2
в кінцевих точках відрізка [– ; ] сума ряду Фур'є набуває
значень
f ( 0) f ( 0)
S( ) S( )
.
2
78.
79.
a 2f ( x 2 ) f ( x)
1
a0
f ( x)dx
a
a 2
1
an
f ( x) cos nxdx, n 1, 2, ...
a
a 2
1
bn
f ( x) sin nxdx, n 1, 2, ...
a
a0 n
f (x) Sn (x)
ak cos kx bk sin kx
2 k 1
80.
ПрикладРозкласти в ряд Фур'є 2 -періодичну функцію:
f ( x) x, x ;
1
1
a0 f ( x)dx ( x)dx
2
1 ( x)
2
2
1
1
an f ( x) cos nxdx ( x) cos nxdx
u x
dv cos nxdx
du dx
1
v sin nx
n
81.
u xdv cos nxdx
du dx
1
v sin nx
n
1 x
1
sin nx sin nxdx 0
n
n
1
1
bn f ( x) sin nxdx ( x) sin nxdx
du dx
u x
1
dv sin nxdx v cos nx
n
1 x
1
cos nx cos nxdx
n
n
82.
1 x1
cos nx cos nxdx
n
n
1 2 ( 1)n
n 1 2
( 1)
n
n
a0 2
an 0
bn ( 1)
n 1
a0
an cos nx bn sin nx
f (x)
2 n 1
( 1)n 1
f ( x ) 2
sin nx.
n
n 1
2
n
83.
84.
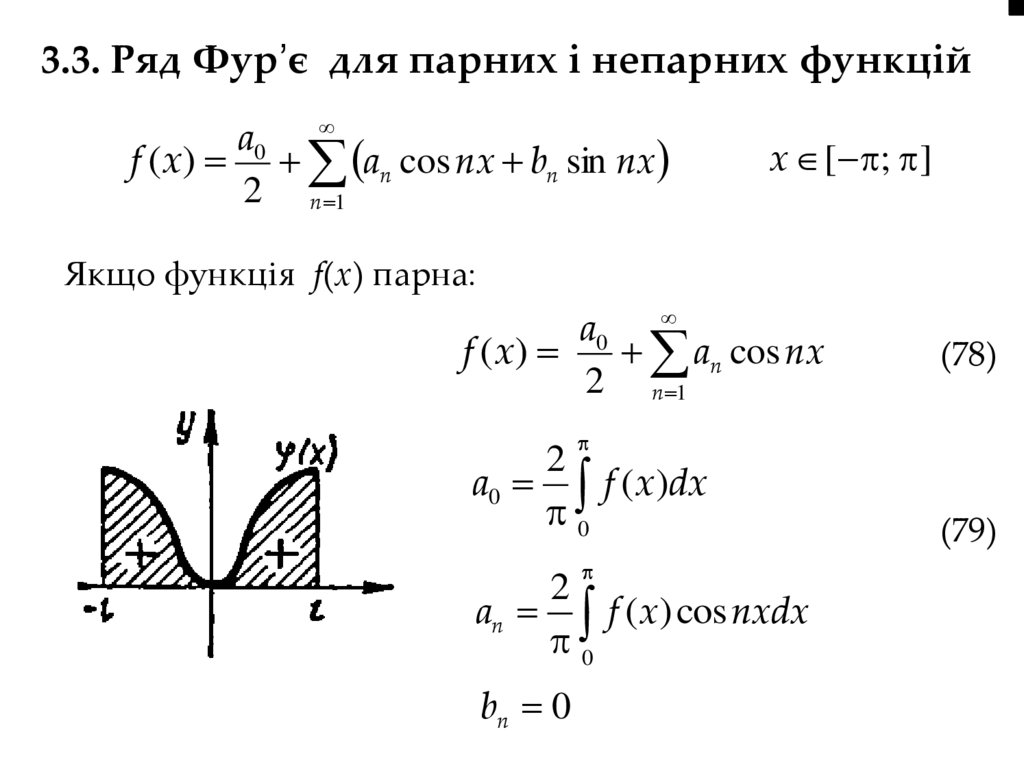
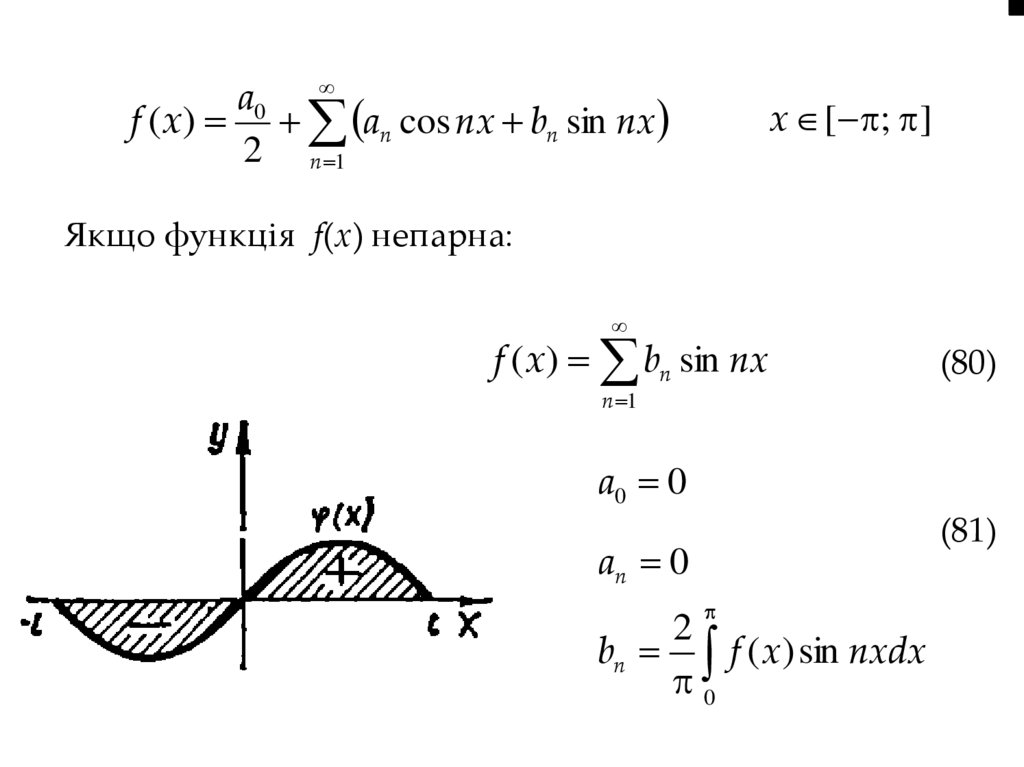
3.3. Ряд Фур’є для парних і непарних функційa0
f (x) an cos nx bn sin nx
2 n 1
x [ ; ]
Якщо функція f(х) парна:
a0
an cos nx
f (x)
2 n 1
(78)
2
a0 f ( x)dx
0
2
an f ( x) cos nxdx
0
bn 0
(79)
85.
a0f (x) an cos nx bn sin nx
2 n 1
x [ ; ]
Якщо функція f(х) непарна:
f (x) bn sin nx
(80)
n 1
a0 0
(81)
an 0
2
bn f ( x) sin nxdx
0
86.
ПрикладРозкласти в ряд Фур'є 2 -періодичну функцію:
f ( x) | x |, x [ ; ]
2
2
2
2 x
a0 f ( x)dx xdx
0
0
2
0
2
2
an f ( x) cos nxdx x cos nxdx
0
0
u x
dv cos nxdx
du dx
1
v sin nx
n
1 2
0
87.
du dx1
v sin nx
n
1
2 1
x sin nx sin nxdx
n0
n
0
u x
dv cos nxdx
cos n ( 1)n
sin n 0
2
2 cos n 1
2
cos nx
n
(
1
)
1
0
2
2
2
2
n
n n
n 0
a0
2 ( 1)n 1
f (x) an cos nx
cos nx
2
2 n 1
2 n 1 n
4 cos x cos 3x cos 5x
2
...
2
2
2 1
3
5
88.
ПрикладРозкласти в ряд Фур'є 2 -періодичну функцію:
1, x [ ; 0)
f ( x)
1, x [0; )
2
2
2
bn f ( x) sin nxdx
sin
nxdx
cos nx
0
0
n
0
2
2
n
n
1
(
1
)
.
( 1) 1
n
n
n
2
1
(
1
)
f (x) bn sin nx
sin nx
n 1
n
n 1
4 sin x sin 3x sin 5x
... .
1
3
5
89.
90.
3.4. Ряд Фур’є 2l-періодичної функціїa0
f (x) an cos nx bn sin nx
2 n 1
lt
x
x [ l; l]
T 2l
lt
(t) f
a0
(t )
an cos nt bn sin nt
2 n 1
t [ ; ]
(85)
91.
a0(t )
an cos nt bn sin nt
2 n 1
t [ ; ]
1
a0 (t )dt
1
an (t ) cos ntdt, n 1, 2, ...
1
bn (t ) sin ntdt, n 1, 2, ...
(85)
92.
xt
l
dt dx
l
(85)
l
1
a0 f ( x)dx
l l
1
nx
an f ( x) cos
dx, n 1, 2, ...
l l
l
l
1
nx
bn f ( x) sin
dx, n 1, 2, ...
l l
l
l
a0
nx
nx
bn sin
f (x) an cos
2 n 1
l
l
(87)
93.
Приклад1. Зобразити рядом Фур'є функцію:
f ( x) x 2
T 2
x ;
l 1
f ( x 2) f ( x)
1 x 1
bn 0
l
1
3 1
1
x
2
a0 f ( x)dx 2 x dx 2
l l
3
0
0
2
.
3
94.
2du 2 xdx
u
x
2
an 2 x cos nx dx
1
sin nx
dv cos nxdx v
0
n
1
1
1
1
4
2
2x
sin nx
x sin nx dx
n
n 0
0
0
du dx
u x
1
v
cos
nx
dv sin nxdx
n
1
1
4 x
1
cos nx
cos
nxdx
n n
n
0
0
0
95.
14x
4 ( 1) n
2 2 cos nx
.
2 2
n
n
0
2
a0 .
3
4 ( 1) n
.
an
2 2
n
bn 0
1 4 ( 1)n
f (x) 2 2 cos nx
3 n 1 n
1 4 cos x cos 2 x cos 3 x cos 4 x
2
...
.
2
2
2
2
3
1
2
3
4
x ;
96.
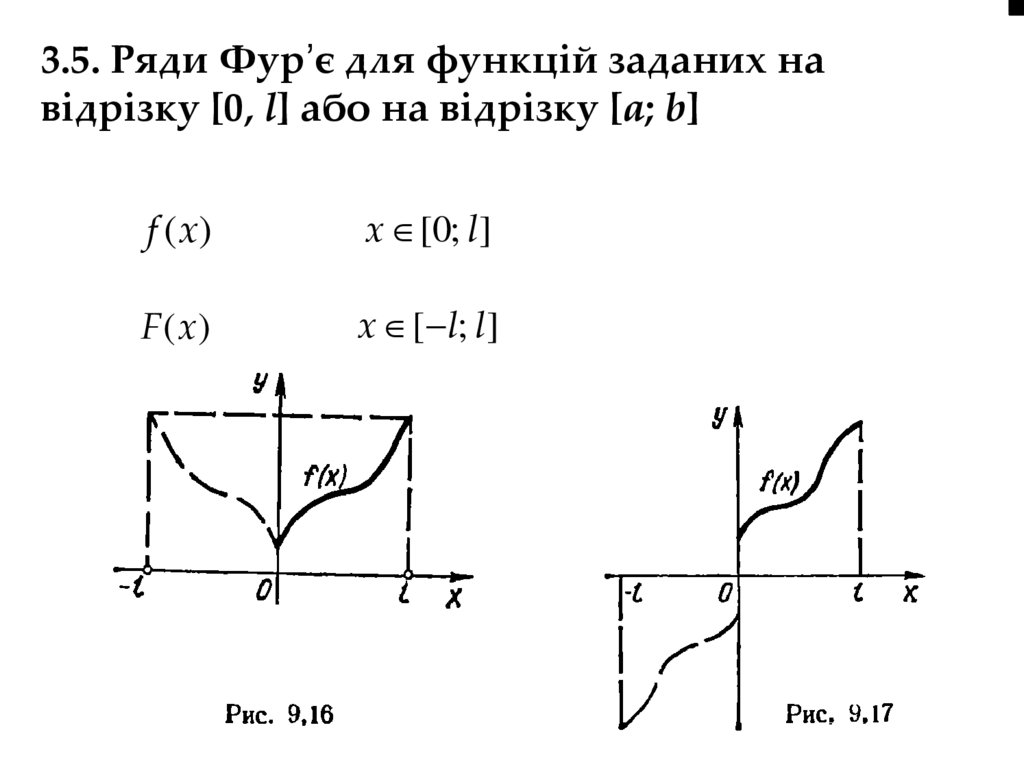
3.5. Ряди Фур’є для функцій заданих навідрізку [0, l] або на відрізку [a; b]
f (x)
x [0; l]
F (x )
x [ l; l]
97.
a0F(x) an cos nx bn sin nx
2 n 1
Якщо функція F(х) парна:
a0
an cos nx
F(x)
2 n 1
Якщо функція F(х) непарна:
F(x)
b
n 1
n
sin nx
x [ l; l]
98.
a0f (x) an cos nx bn sin nx
2 n 1
x [ a; b]
Приклад
Зобразити рядом Фур'є функцію:
f ( x) x
x [1; 3]
b
1
a0 f ( x)dx
la
1
nx
an f ( x) cos
dx, n 1, 2, ...
la
l
b
1
nx
bn f ( x) sin
dx, n 1, 2, ...
la
l
b
2l 2
l 1

















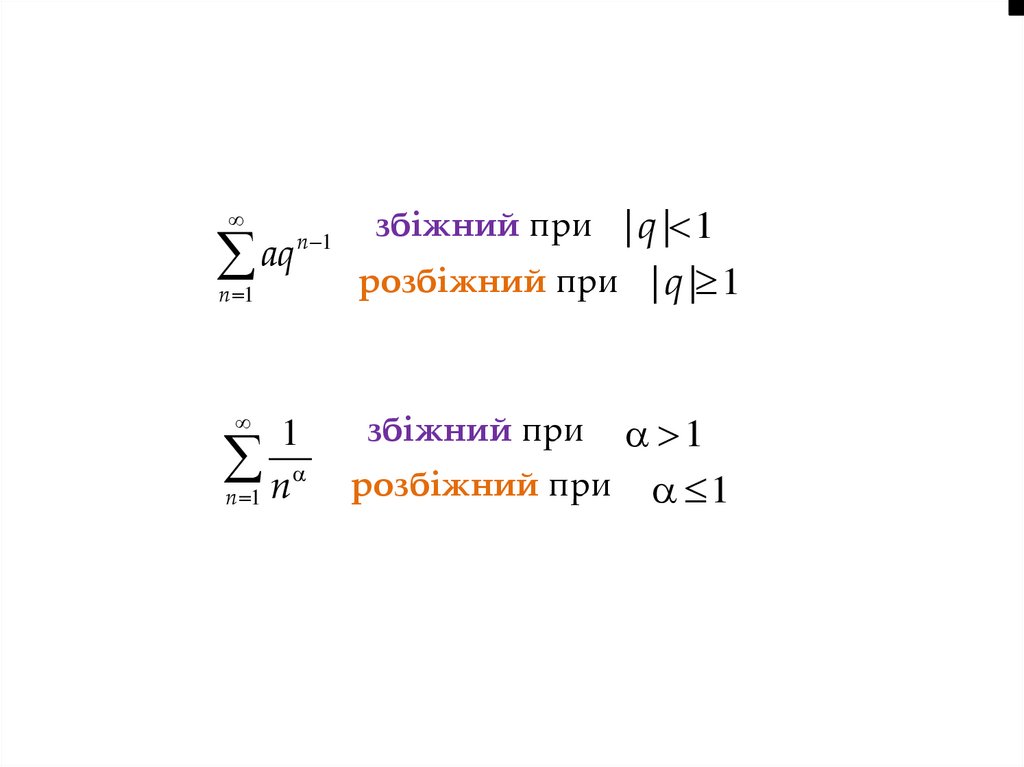






































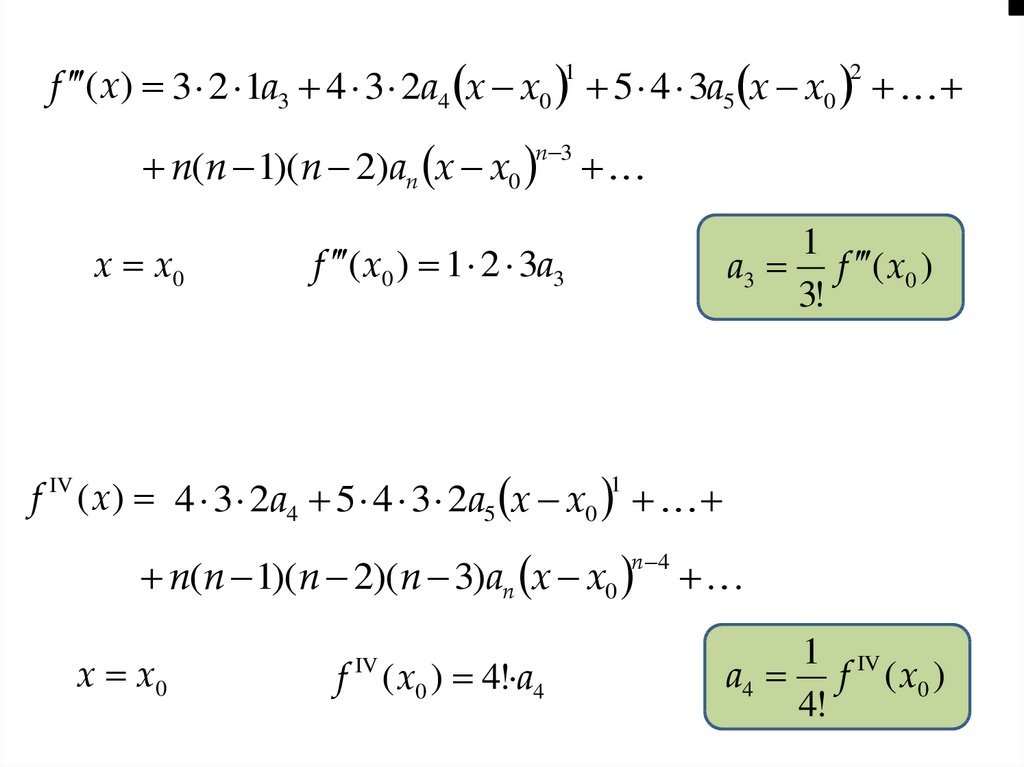





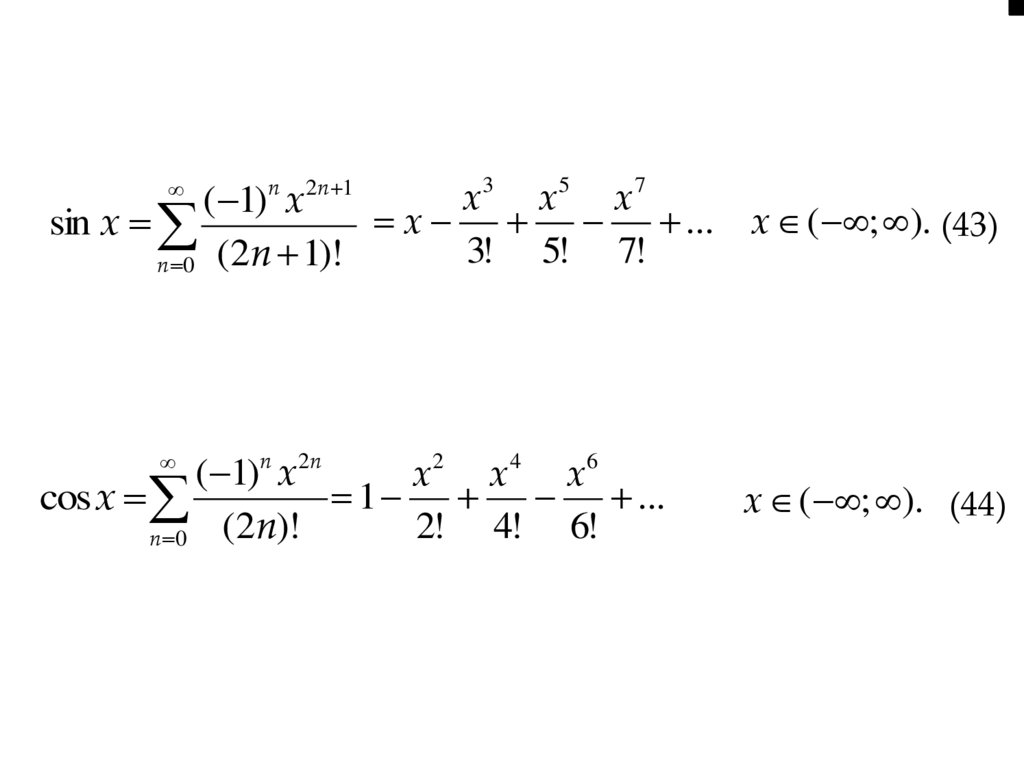
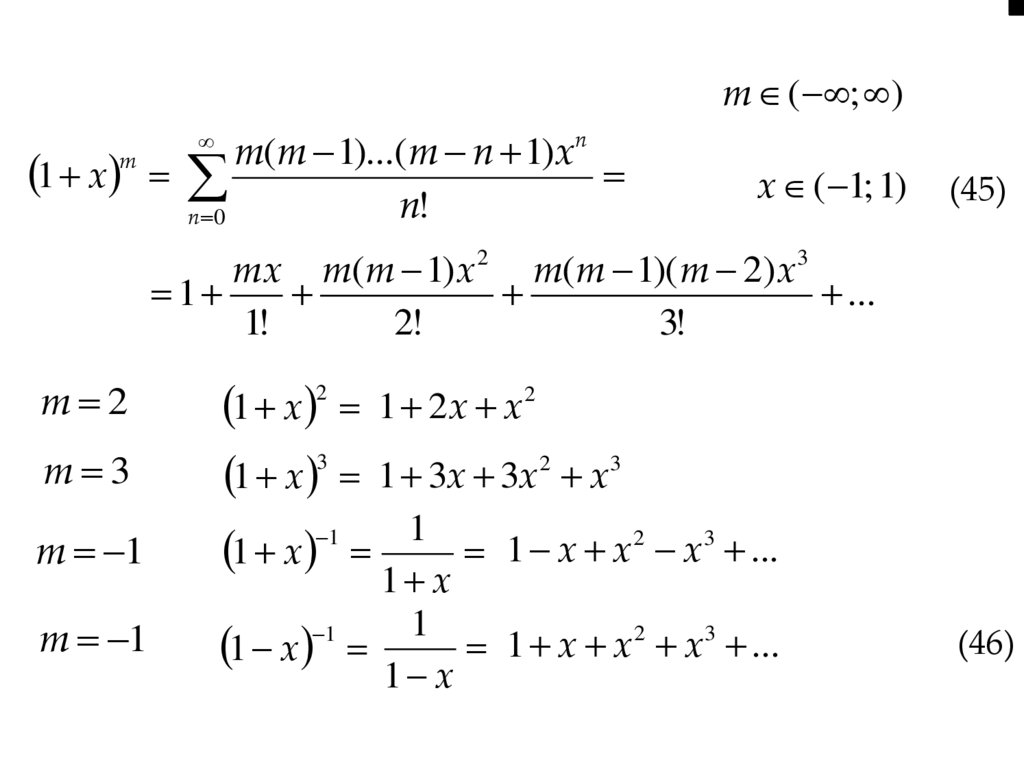
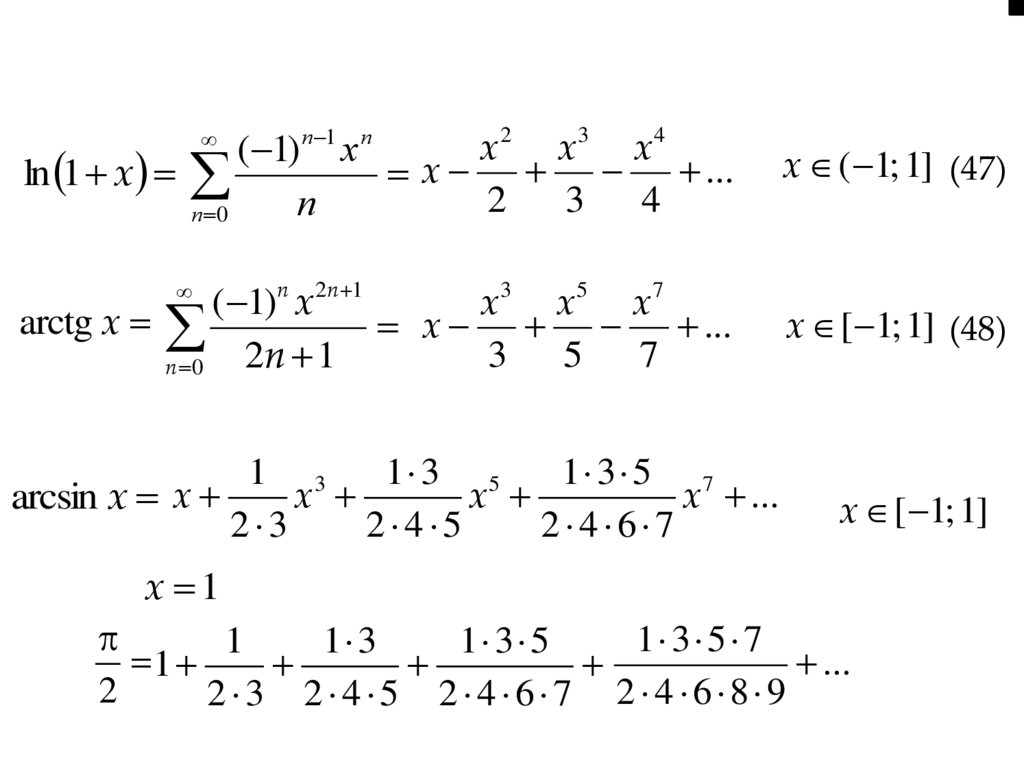








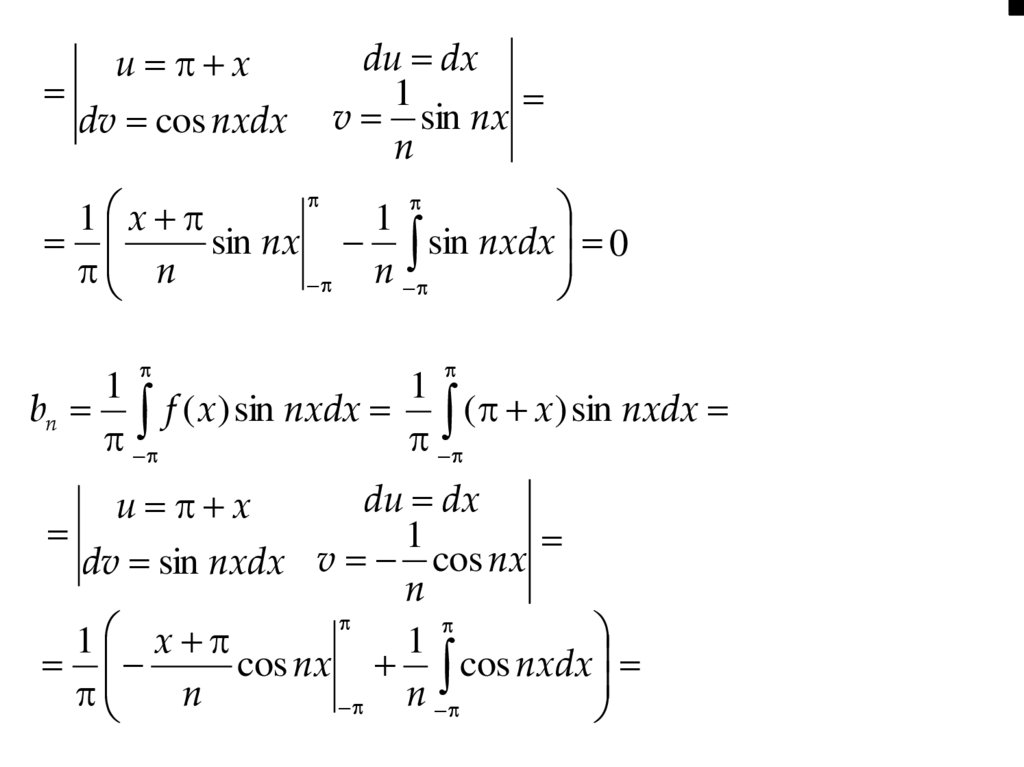
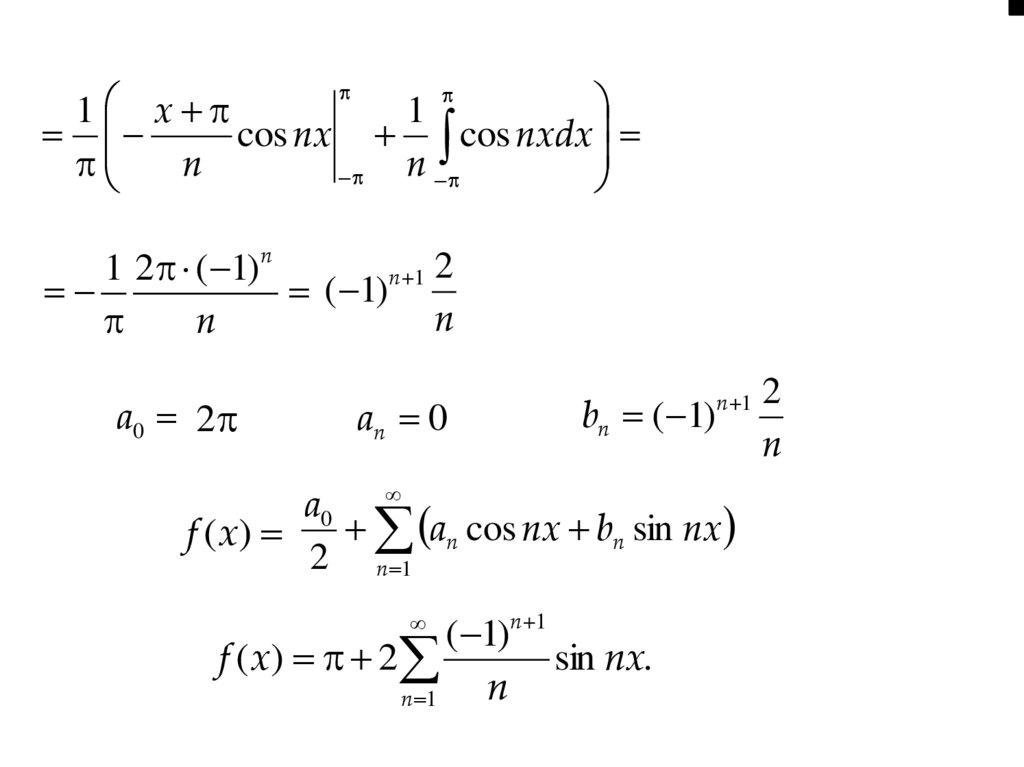




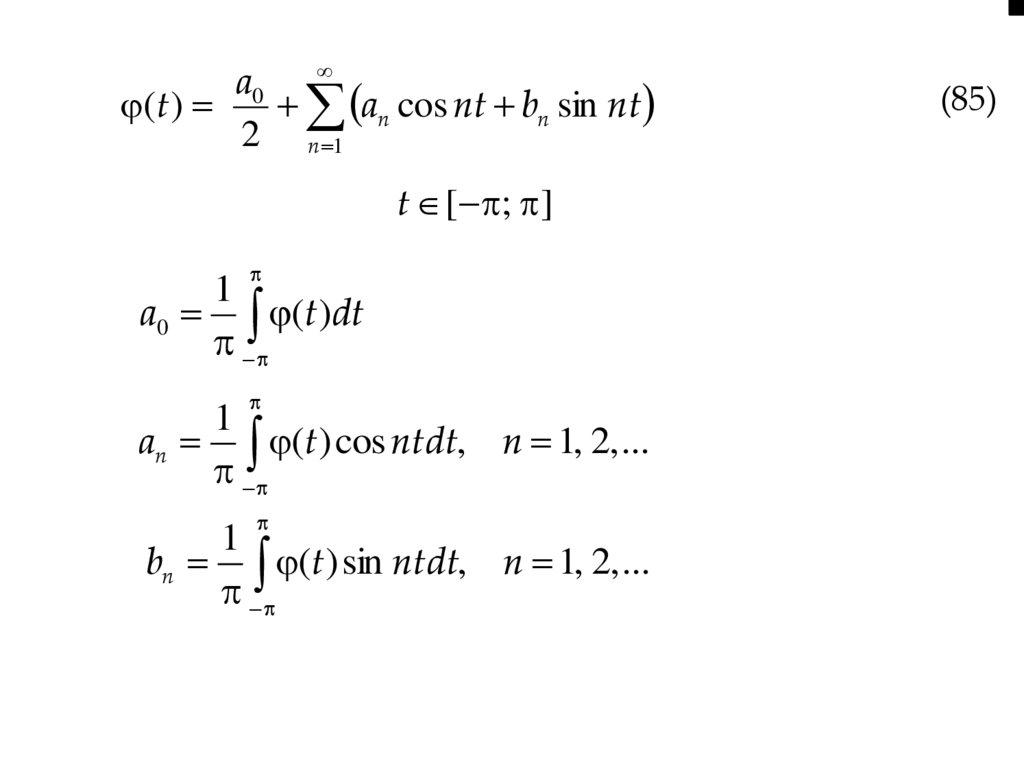


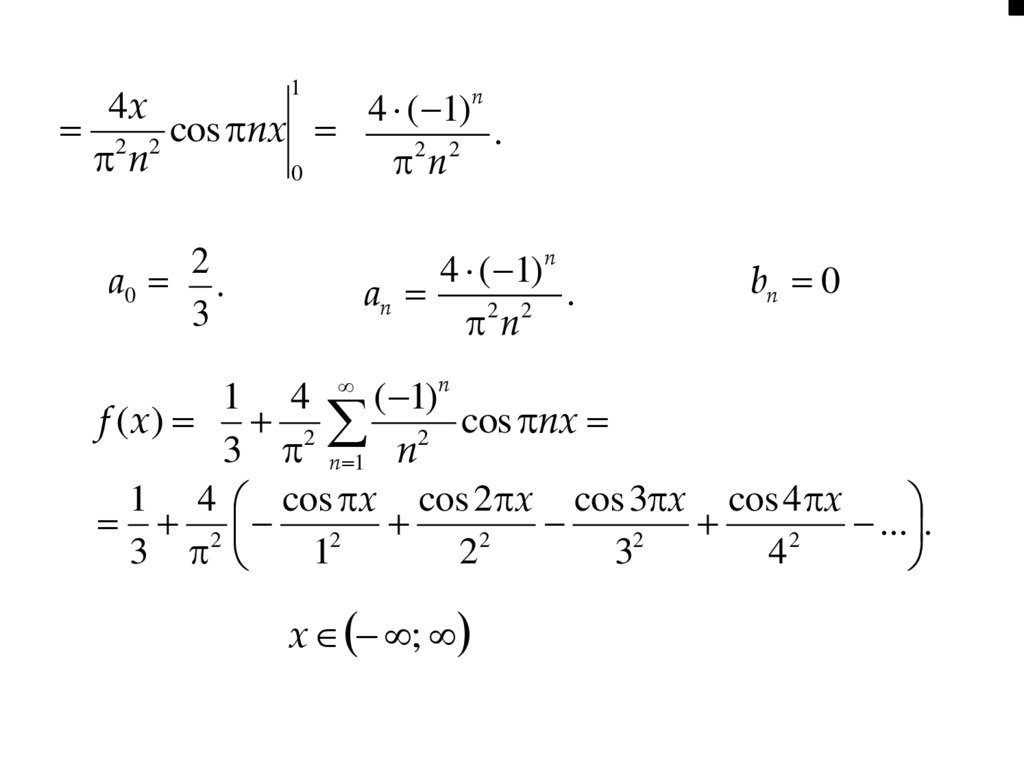










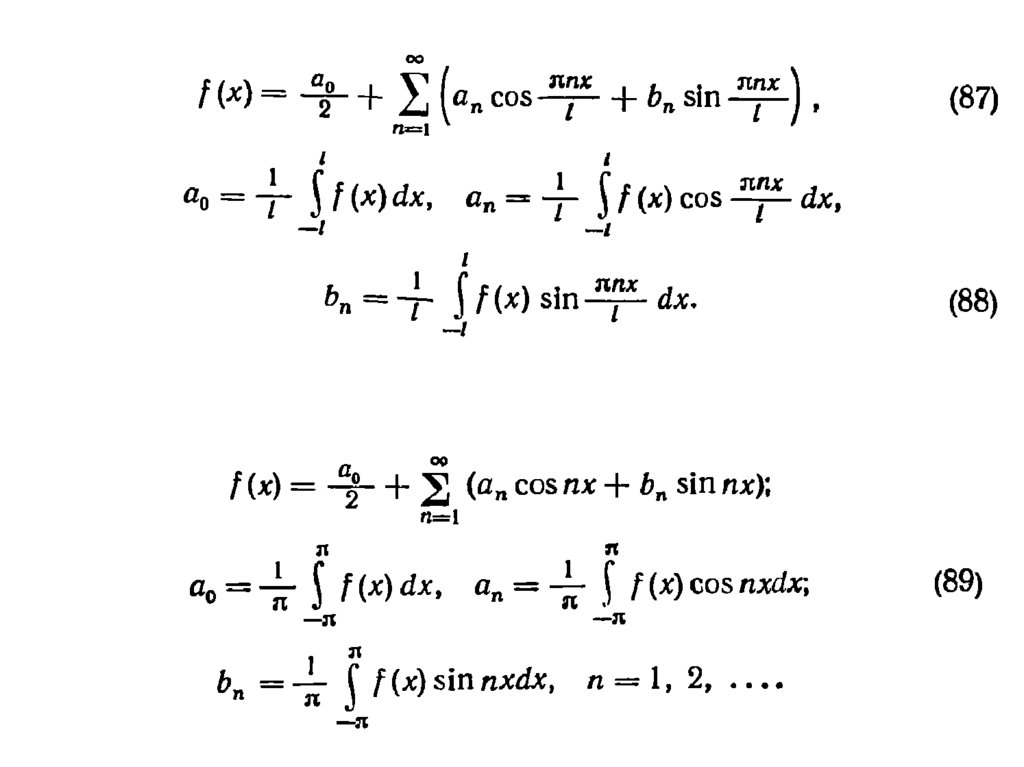





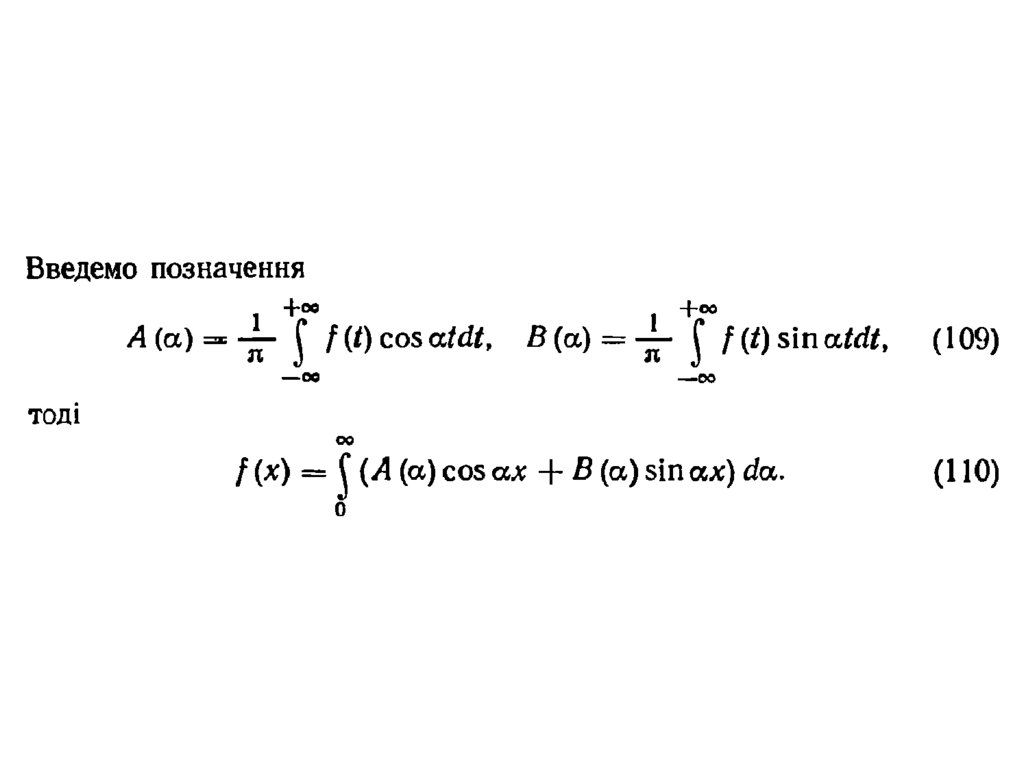








 Математика
Математика








