Похожие презентации:
Арифметический квадратный корень
1.
2. Цели урока:
• Рассмотреть определениеарифметического квадратного корня;
• Научиться находить арифметические
квадратные корни;
• Работать над развитием
математической речи.
3. Тест
1.Вычислить: 62А) 12;
Б) 36;
В) 8;
Г) не знаю.
2. Вычислить: 0,82
А) 6,4;
Б) 1,6;
В) 0,64;
3. Вычислить: - 72
А) 49; Б) - 49; В) 14;
Г) – 14.
4. Вычислить (-0,05)2
А) 0,1;
Б) 0,0025; В) -0,0025;
Г) 0,16.
Г) -0,1
5. Какое число или числа нужно поставить вместо х, чтобы
получилось верное равенство х2 = 16?
А) 4; Б) - 4; В) 4 или - 4; Г) 8 или -8.
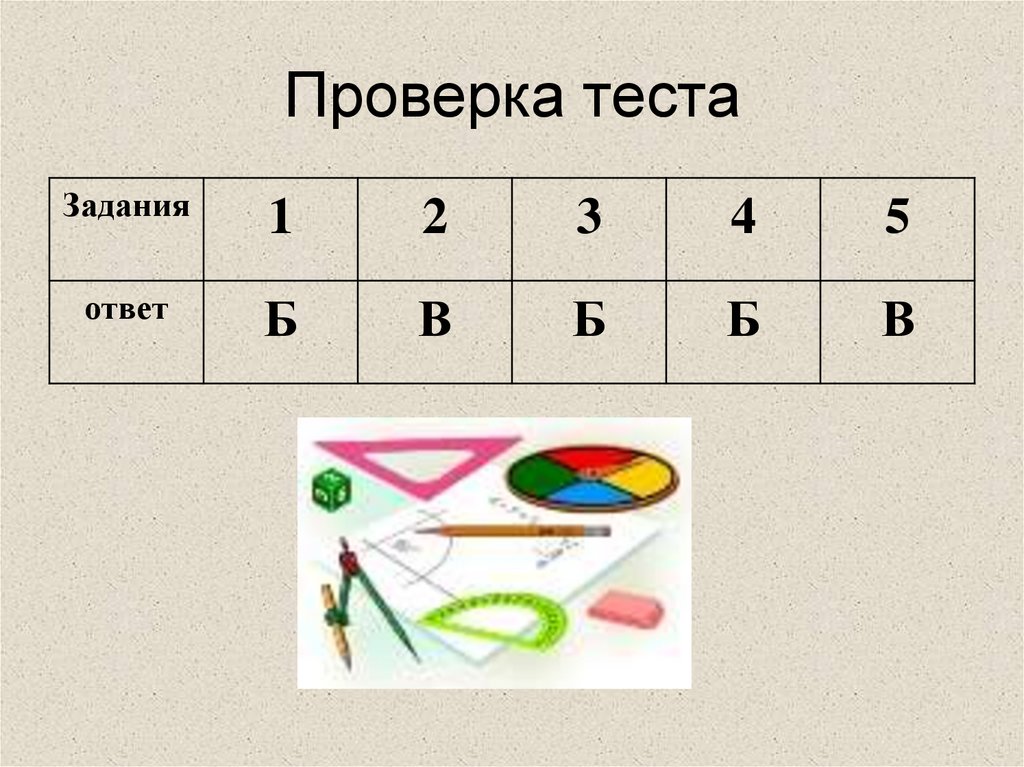
4. Проверка теста
Задания1
2
3
4
5
ответ
Б
В
Б
Б
В
5.
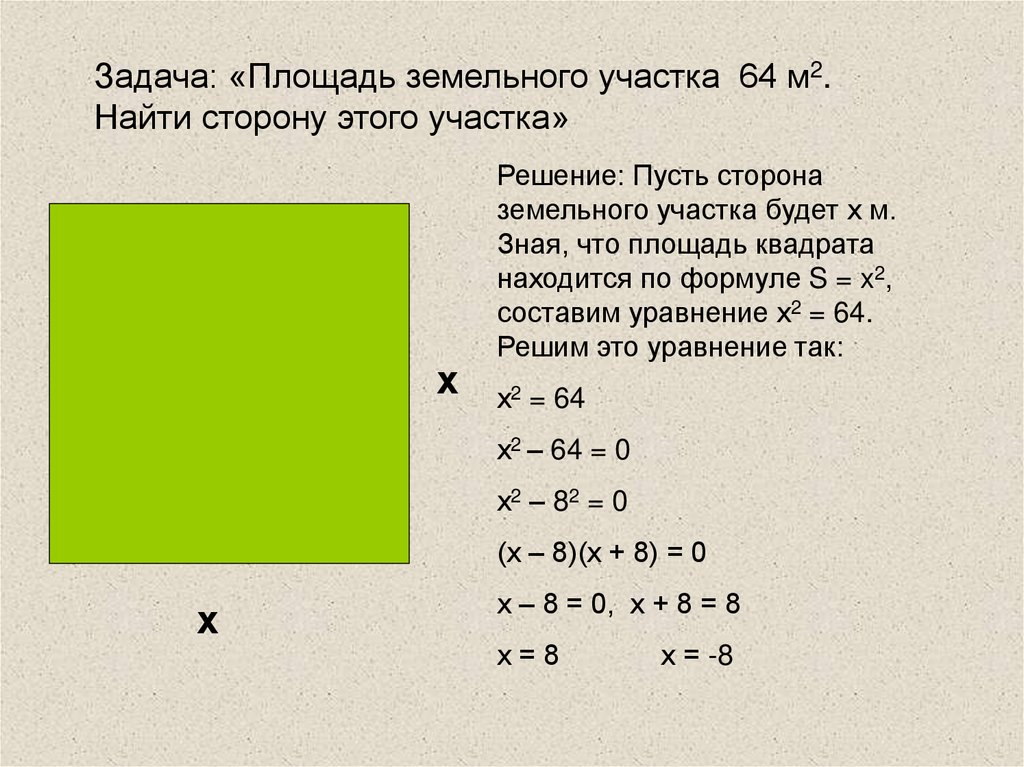
Задача: «Площадь земельного участка 64 м2.Найти сторону этого участка»
х
Решение: Пусть сторона
земельного участка будет х м.
Зная, что площадь квадрата
находится по формуле S = x2,
составим уравнение х2 = 64.
Решим это уравнение так:
х2 = 64
х2 – 64 = 0
х2 – 82 = 0
(х – 8)(х + 8) = 0
х
х – 8 = 0, х + 8 = 8
х=8
х = -8
6.
Числа 8 и – 8 называются квадратными корнями из числа 64. Одноиз них положительное. Это число называют арифметическим
квадратным корнем и обозначают
. Таким образом,
64
64 Арифметическим
8
Определение:
квадратным корнем из числа а
называется неотрицательное число, квадрат которого равен
а.
à
Подкоренное выражение
«Арифметический квадратный корень из числа а»
9;
0,49 ;
100 ;
121;
4
;
9
1
2 ;
4
25
7. Важно!
Выражениеà имеет смысл только при а ≥ 0.
При любом а, при котором выражение имеет смысл,
верно равенство:
а а
2
Например :
2
1
1
;
3 3;
2
2
2
0,6 0,6
2
8. Найти значение корня:
8136
1600
10000
0,04
0,81
81
4
24
1
25
9. Имеет ли смысл выражение:
100 ;100 ;
100 ;
( 10) ;
2
( 25) ( 4) ;
25 4







 Математика
Математика








