Предмет стереометрии

1.

2.

Стереометрия —
раздел геометрии,
в котором
изучаются
свойства фигур в
пространстве.

3.

Основными (простейшими) фигурами в пространстве
являются точки, прямые и плоскости. В стереометрии
появляется новый вид взаимного расположения
прямых: скрещивающиеся прямые. Это одно из немногих
существенных отличий стереометрии от планиметрии, так
как во многих случаях задачи по стереометрии решаются
путем рассмотрения различных плоскостей, в которых
выполняются планиметрические законы.
Не стоит путать этот раздел с планиметрией, поскольку в
планиметрии изучаются свойства фигур на плоскости
(свойства плоских фигур), а в стереометрии — свойства
фигур в пространстве (свойства пространственных фигур).

4.

В стереометрии наряду
с простейшими
фигурами – точками,
прямыми и плоскостями
– рассматриваются
геометрические тела и
их поверхности.
Представление о
геометрических телах
дают окружающие нас
предметы. Например,
кристаллы имеют
форму геометрических
тел, поверхности
которых составлены из
многоугольников. Такие
поверхности
называются
многогранниками.

5.

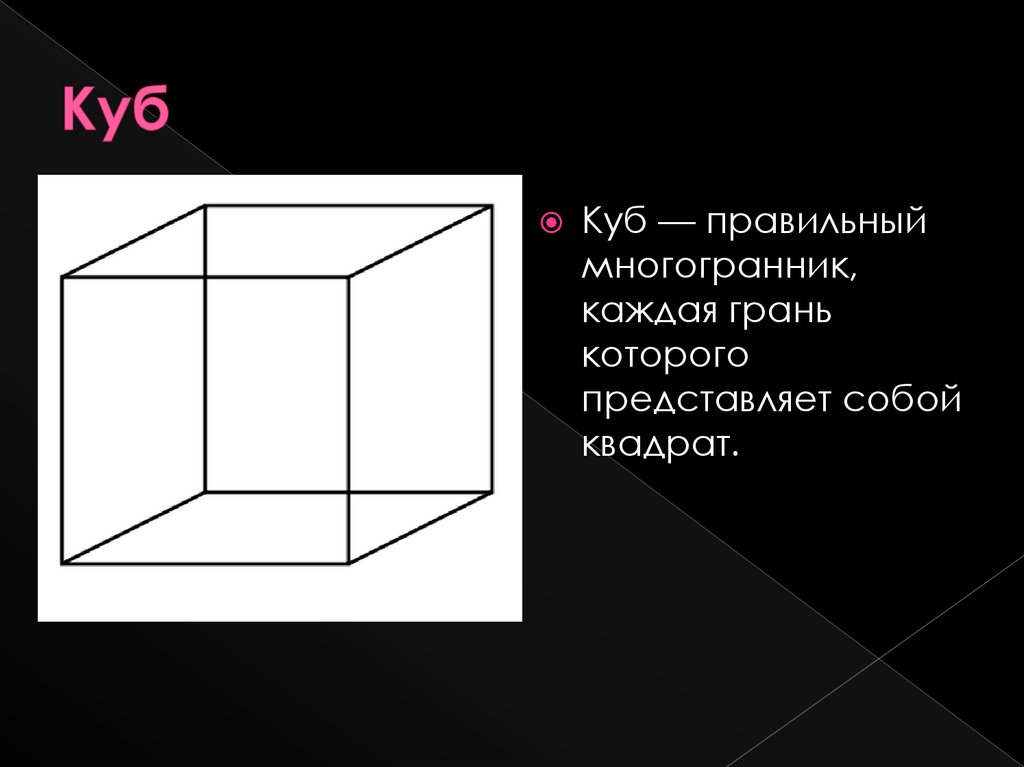
Куб — правильный
многогранник,
каждая грань
которого
представляет собой
квадрат.

6.

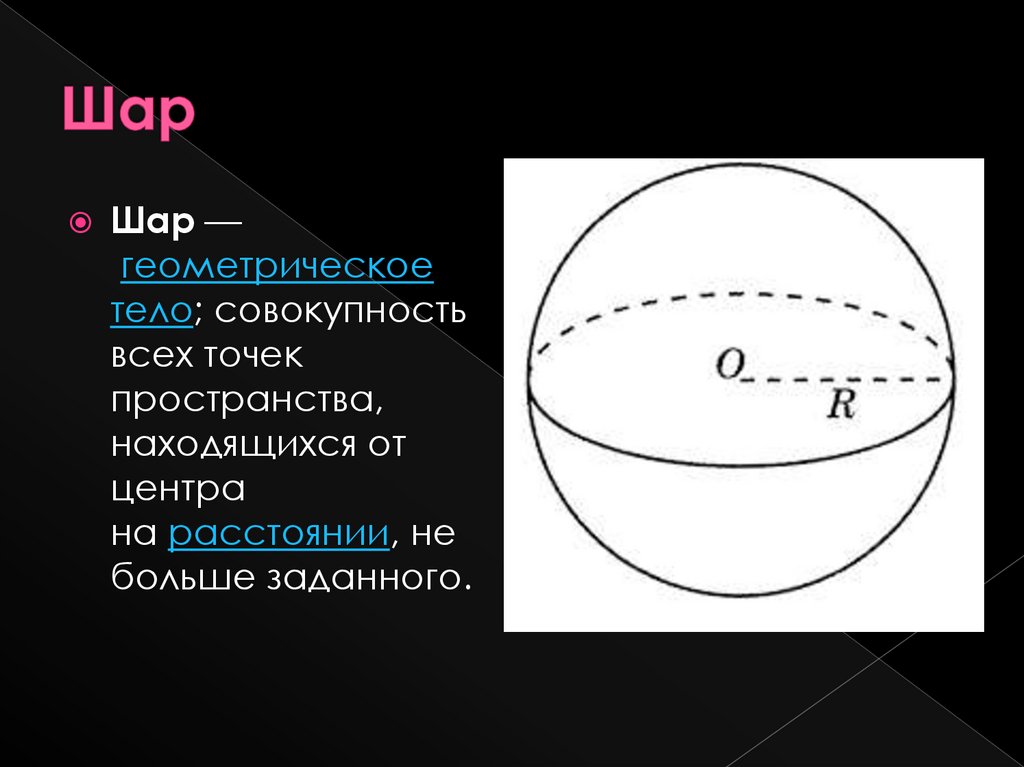
Шар —
геометрическое
тело; совокупность
всех точек
пространства,
находящихся от
центра
на расстоянии, не
больше заданного.

7.

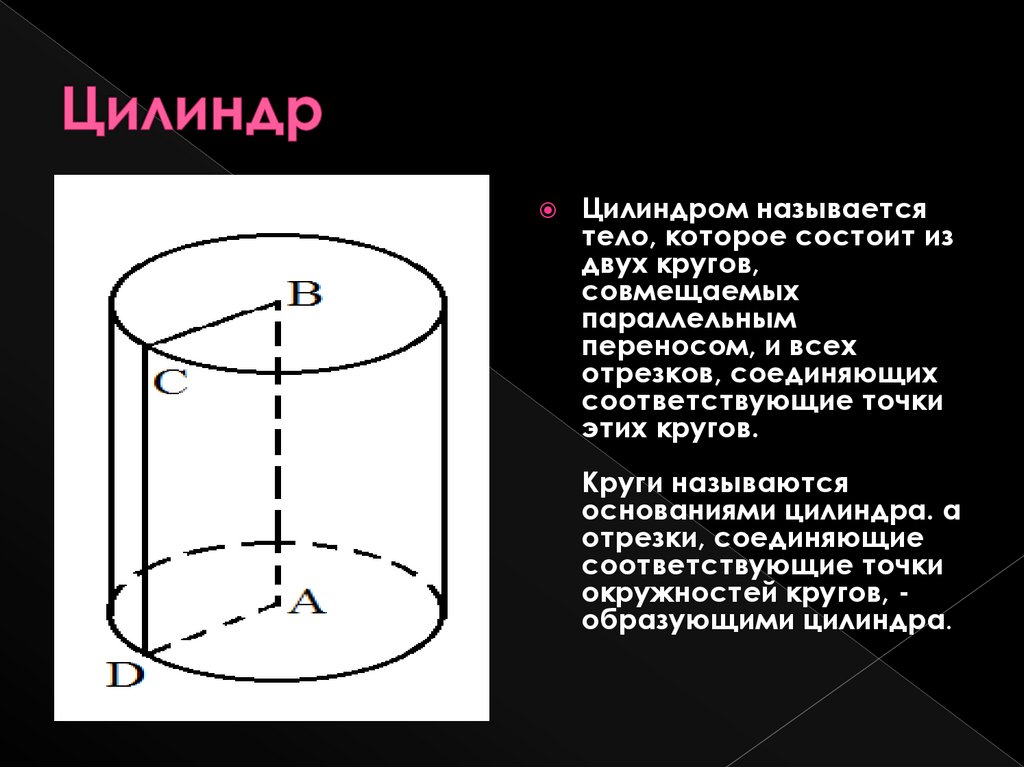
Цилиндром называется
тело, которое состоит из
двух кругов,
совмещаемых
параллельным
переносом, и всех
отрезков, соединяющих
соответствующие точки
этих кругов.
Круги называются
основаниями цилиндра. а
отрезки, соединяющие
соответствующие точки
окружностей кругов, образующими цилиндра.

8.

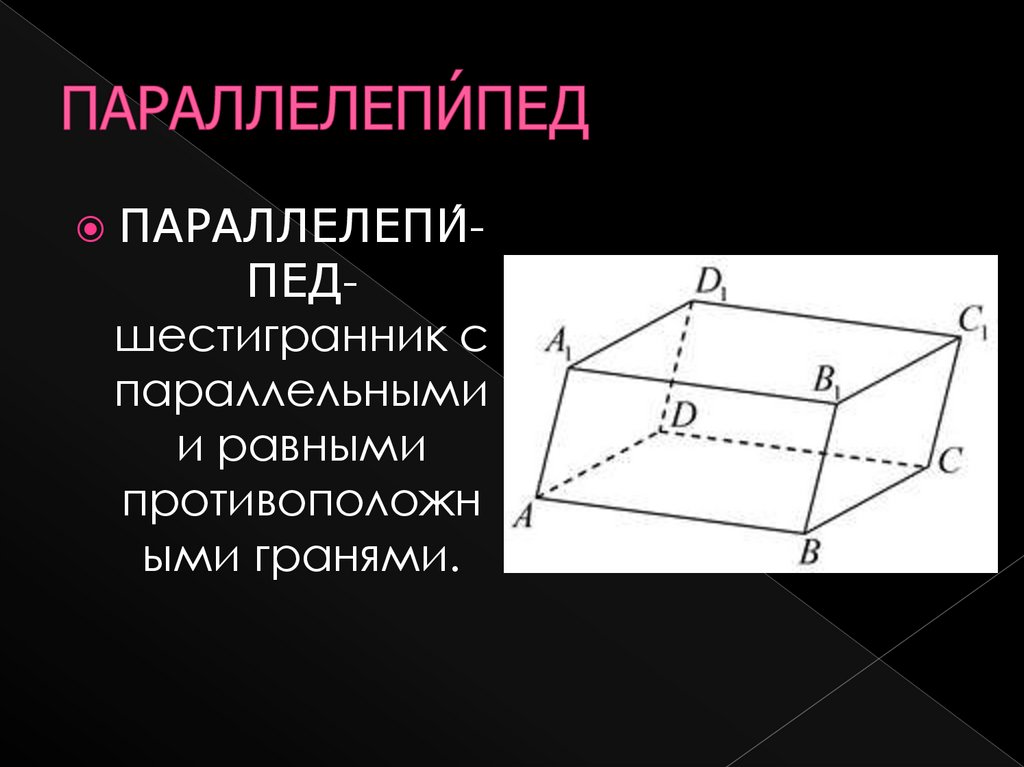
ПАРАЛЛЕЛЕПИ́-
ПЕДшестигранник с
параллельными
и равными
противоположн
ыми гранями.

9.

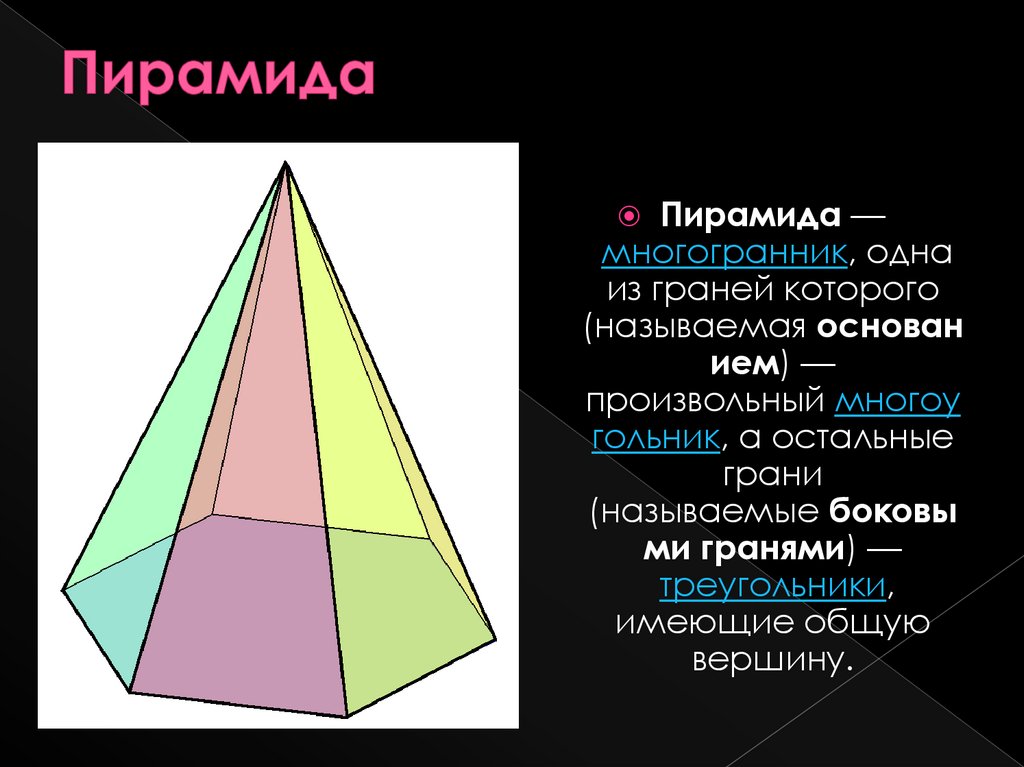
Пирамида —
многогранник, одна
из граней которого
(называемая основан
ием) —
произвольный многоу
гольник, а остальные
грани
(называемые боковы
ми гранями) —
треугольники,
имеющие общую
вершину.

10.

Конус —
тело, полученное объеди
нением всех лучей, исход
ящих из одной точки (вер
шины конуса) и проходя
щих через плоскую повер
хность. Иногда конусом н
азывают часть такого тела,
полученную объединени
ем всех отрезков, соедин
яющих вершину и точки пл
оской поверхности (посл
еднюю в таком случае на
зывают основанием конус
а, а конус называют опир
ающимся на данное осн
ование).