Теория надежности. Вероятность безотказной работы и вероятность отказа. Распределение Вейбулла

1. Наработка

Пусть в момент t=0 элемент начинает работу, а в
момент t=T происходит отказ.
0
T
T – cлучайная величина
Вероятность безотказной работы
Р(t) = P(T > t)
Вероятность отказа
Q (t ) P (T t ),
Q (t ) 1 P (t )

2.

Вероятность безотказной работы P(t) и
отказа Q(t).
вероятность

3. Свойства

1. P(0) =1.
2. P(t) 0 при t
Вероятность безотказной работы по
статистическим данным об отказах
оценивается выражением
P (t ) ( N0 n (t )) / N0
n(t) – число отказавших изделий

4.

Если хотим найти функцию P(t) для всех значений
t t0 , то в процессе испытаний необходимо отмечать
моменты возникновения отказов.
Отношение
P (t) N n(t )
N
N
называется эмпирической функцией надежности.
С ростом N эта функция равномерно
приближается к функции P(t), и для больших
N имеет место соотношение
P (t) N n(t) P(t)
N
N

5. Вероятность отказа

Интегральный закон распределения случайной
величины T в теории надежности называют
вероятностью отказа и обозначают Q(t).
Q (t ) P (T t )
Q (t ) P (t ) 1
Функция плотности вероятности времени безотказной работы
характеризует плотность, с которой распределено значение случайной
величины в окрестности данной точки
q(t) dQ(t) d (1 P(t)) dP(t).
dt
dt
dt

6.

Плотность
распределения
является
q(t )
дифференциальной формой закона распределения
времени безотказной работы (наработки до отказа) Т.
Плотность q(t ) является неотрицательной функцией,
причем
q(t )dt 1.
0
Вероятность безотказной работы и вероятность отказа
связаны с частотой отказа q(t ) соотношениями
t
P(t) 1 q( x)dx q( x)dx;
0
t
t
Q(t ) q( x)dx.
0

7. Интенсивность отказов

Одной из наиболее распространенных
количественных характеристик надежности
является интенсивность отказов, которую
обозначают буквой .
Условную вероятность отказа объекта в
течение наработки (t,t dt) в предположении его
безотказной работы до момента t обычно выражают
где величиной (t ) называется интенсивностью
отказов.

8.

Таким
образом,
при
использовании (t )
рассматриваются лишь остающиеся работоспособными к моменту t объекты, а отказавшие исключаются
из рассмотрения.
dp(t )
q
(
t
)
(t )
dt ,
p(t )
p(t )
(6)
Решение уравнения (6) при начальном
условии p(0) 1 дает для функции надежности
формулу
t
( x)dx
t
0
p(t ) e
exp ( x)dx .
0
(7)

9.

При const
упрощается:
формула
(7)
существенно
p (t ) exp( t ).
(8)
Вероятность безотказной работы в течение
(t1, t2 )
наработки
объекта, который был
работоспособным к началу этого интервала,
p(t1, t2 )
t2
exp ( x)dx
p(t2 )
0
p(t1)
t1
exp ( x)dx
0
t2
exp ( x)dx .
t1
(9)

10.

При const вероятность безотказной работы в
течение наработки (t1, t2 ) не зависит от возраста объекта:
p(t1, t2 ) p(t ) exp( t ),
(10)
где t t2 t1.
При t 1 обычно полагают:
exp( t ) 1 t .
Статистически интенсивность отказов определяется
как отношение числа отказавших элементов в единицу
времени к среднему числу элементов, продолжающих
исправно работать.
(t )
где
n
n
,
Nср ( t ) t
- число элементов, отказавших за время
(11)
t

11.

Ni 1 Ni
Nср
2
(12)
- число исправно работающих элементов в
начале интервала,
Ni - число исправно работающих элементов в
конце интервала времени t .
Интенсивность отказов показывает, какая часть
элементов выходит из строя в единицу времени
(обычно в час), другими словами, показывает,
сколько отказов следует ожидать в единицу
времени.
Ni 1

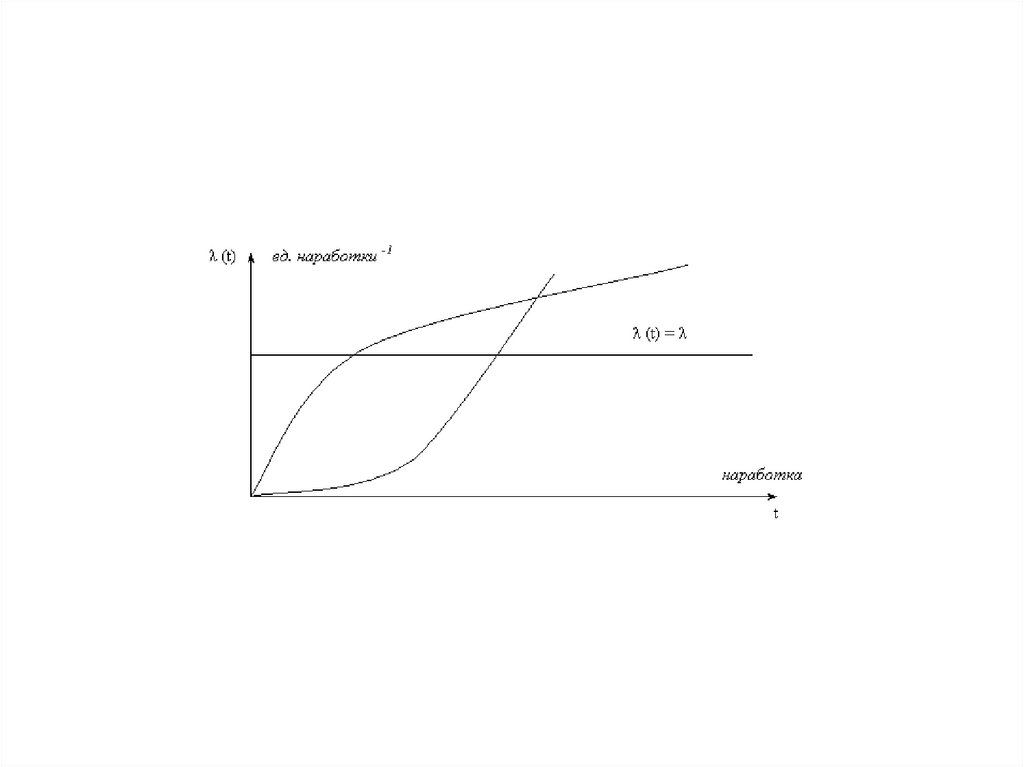
12. Согласно установившимся в теории надежности представлениям кривая имеет вид, показанный на рис.2.

Рис.2. Типичная кривая интенсивности отказов.

13.

14. Среднее время безотказной работы

Часто при расчетах пользуются характеристикой
Тср, которая представляет собой математическое
ожидание непрерывной неотрицательной случайной
величины T – времени безотказной работы
(наработки на отказ) и называется средним временем
безотказной работы (средней наработкой на отказ).
математического
определению
Согласно
ожидания непрерывной случайной величины
dQ(t )
dt
Tcp M [T ] tq(t )dt t
dt
0
dP(t )
dt.
t
dt
0
0

15.

Интегрируя по частям, получаем:
Tcp tP(t )
0 P(t )dt.
0
Первое слагаемое в этом равенстве
tP(t )
t 1 Q(t ) 0.
0 t 1 Q(t ) 0 tlim
Это можно пояснить следующими рассуждениями.
Вероятность отказа становится равной 1 уже при конечном (но
достаточно большом) времени работы, следовательно, выражение
1 Q(t ) 0
t.
уже при конечном

16.

Таким образом, среднее время безотказной работы
Τ cp P(t ) dt.
0
При = const имеем
Tcp exp( t )dt 1 .
0
(15)
Статистически (на основании испытаний) среднее
время безотказной работы можно оценить следующим
образом
N
Tcp 1 tk ,
N k 1
(16)
где N – число однотипных элементов, над которыми
проводятся испытания;tk - время безотказной работы k-го
элемента.

17.

Нормальное распределение (Гаусса)
Параметр b характеризует форму кривой f(t), т. е.
рассеивание случайной величины T. Кривая ПРО f(t)
тем выше и острее, чем меньше b

18.

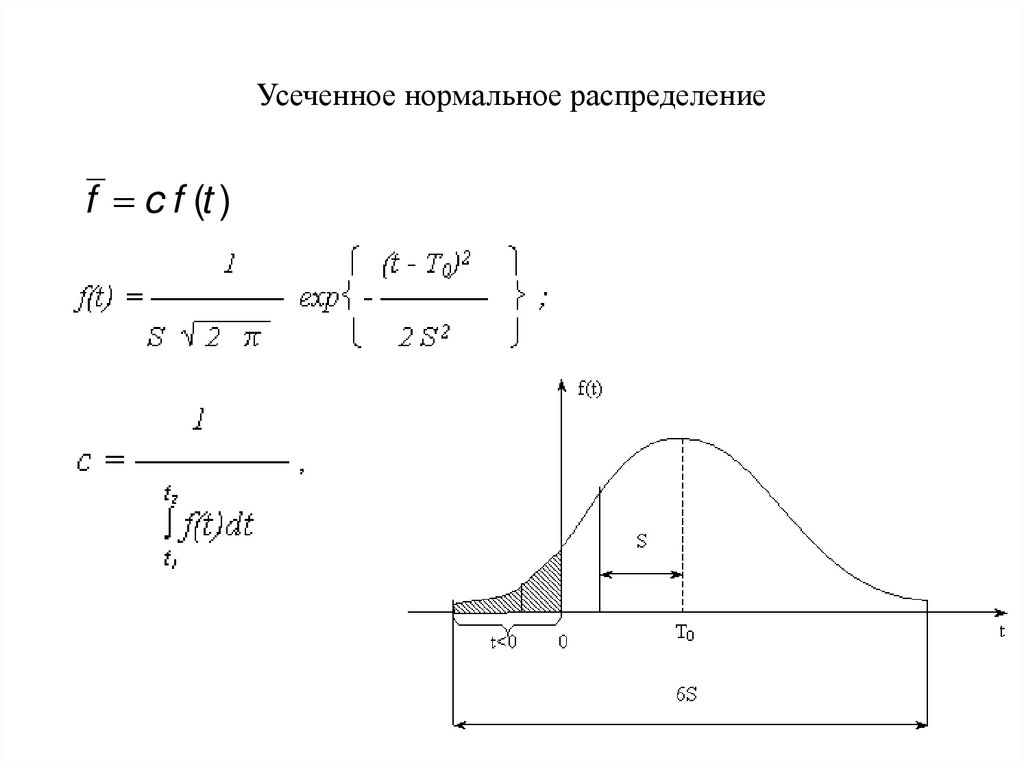
19. Усеченное нормальное распределение

_
f c f (t )

20.

21.

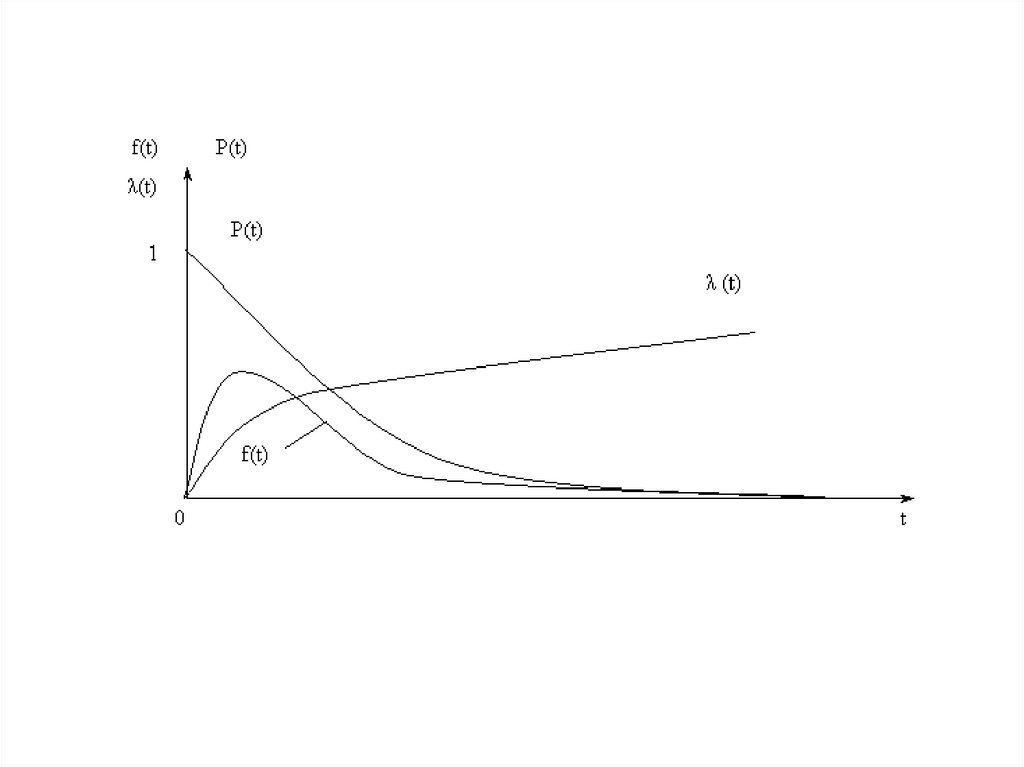
Экспоненциальное распределение

22. Экспоненциальное распределение

f (t ) e
t
Экспоненциальное распределение описывает наработку до
отказа объектов, у которых отсутствует период приработки, а
назначенный ресурс установлен до окончания периода
нормальной эксплуатации.
Эти объекты можно отнести к «не стареющим.
Круг таких объектов широк: сложные технические системы с
множеством компонентов, средства вычислительной техники
и системы автоматического регулирования и т. п.
Экспоненциальное распределение широко применяется для
оценки надежности энергетических объектов.

23.

Логарифмически нормальное распределение
При логарифмически нормальном распределении нормально
распределенным является логарифм (lg t) случайной величины T, а
не сама эта величина.
Логарифмически нормальное распределение во многом более
точно, чем нормальное описывает наработку до отказа тех
объектов, у которых отказ возникает вследствие усталости,
например, подшипников качения, электронных ламп и пр.
f (t )
1
t 2
e
(ln t )2 / (2 2 )

24.

25. Гамма-распределение

Гамма-распределение наиболее хорошо описывает
распределение суммы независимых случайных
величин, каждая из которых распределена по
экспоненциальному закону

26.

27.

Распределение Вейбулла
k 1 0t k
f ( t ) kt
e
0
( t ) kt
0
k 1