Анализ мат. моделей на чувствительность (лекция 3.1)

1.

Анализ мат. моделей на чувствительность
• Анализ чувствительности оптимального решения к определенным
изменениям исходной модели.
• Рассматривается некоторая совокупность оптимизационных моделей, т.е. по
сути некоторая модель исследования операций
• Возникает возможность анализа влияния возможных изменений исходных
условий на полученное ранее оптимальное решение
• Отсутствие такой возможности может привести к такой ситуации, что
принятое решение «устареет» еще до своей реализации.

2.

Анализ мат. моделей на чувствительность
• Связывающие (активные) ограничения – ограничения, график
которых (прямая) проходит через оптимальную точку
• Несвязывающие (неактивные) ограничения – ограничения ,
график которых не проходит через оптимальную точку
• Ресурсы относящиеся связанным ограничениям являются
дефицитными ресурсами
• Ресурсы относящиеся несвязанным ограничениям являются
недефицитными ресурсами

3.

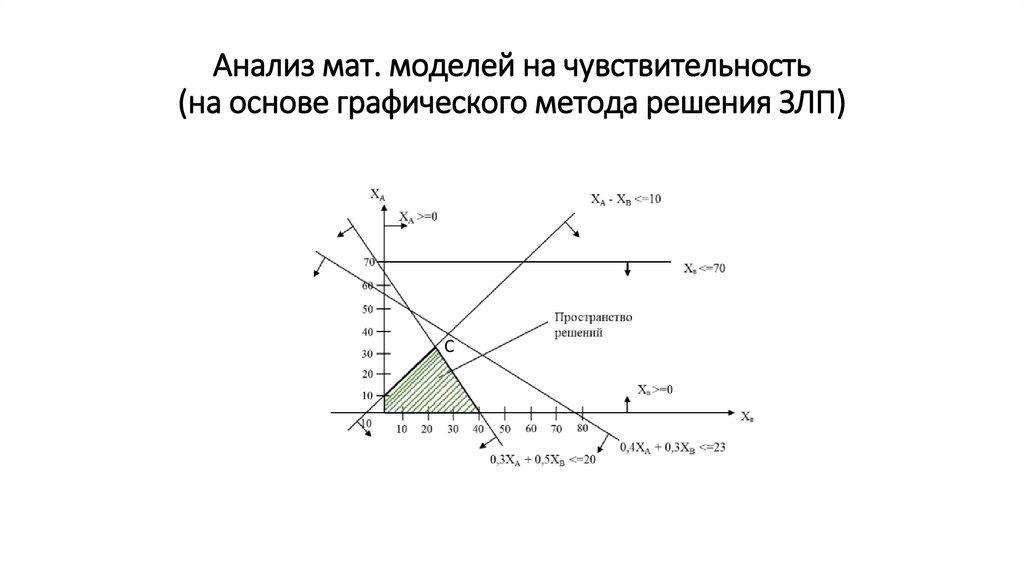
Анализ мат. моделей на чувствительность
(на основе графического метода решения ЗЛП)
C

4.

Анализ мат. моделей на чувствительность
1) На сколько можно увеличить запас некоторого ресурса
(дефицитного) для улучшения значения целевой функции Z?
2) На сколько можно снизить запас некоторого ресурса
(недефицитного) при сохранении полученного значения
целевой функции Z?
3) Увеличение объема какого ресурса наиболее выгодно?
4) В каких пределах допустимо изменение коэффициентов целевой
функции?

5.

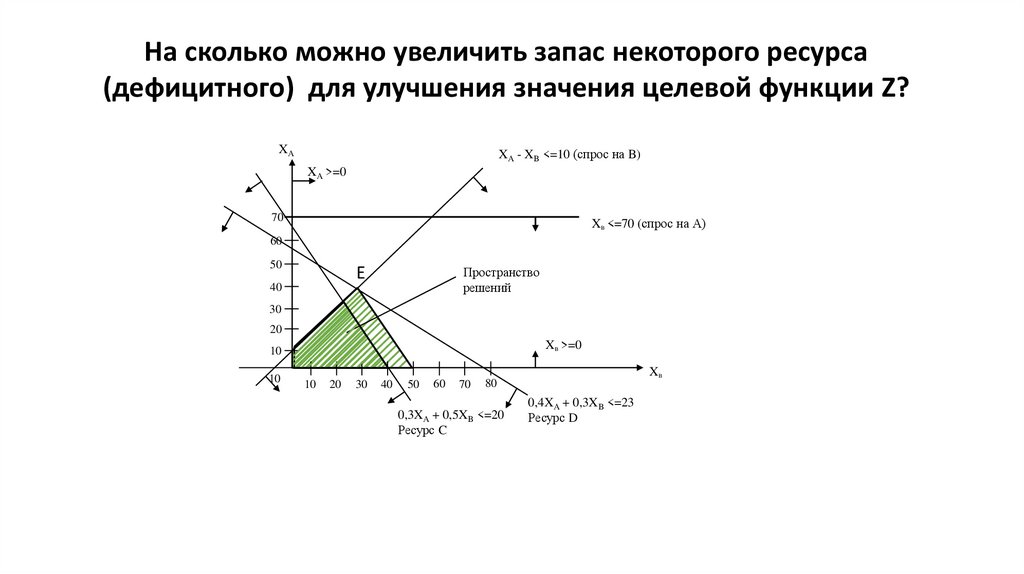
На сколько можно увеличить запас некоторого ресурса
(дефицитного) для улучшения значения целевой функции Z?
В нашем примере дефицитным ресурсом является запасы сырья С,
а запасы сырья Д – избыточным.
Это означает что ресурс С сдерживает рост доходности
предприятия.
На параметры спроса на рынке прямого влияния у предприятия нет
С точки зрения увеличения доходности, естественно нас волнует
вопрос – при существующих условиях по рынку спроса, какой
объем ресурса С мы сможем увеличить и сколько прироста
доходности даст каждая единица приращенного дефицитного
ресурса С

6.

На сколько можно увеличить запас некоторого ресурса
(дефицитного) для улучшения значения целевой функции Z?
XA
XA - XB <=10 (спрос на B)
XA >=0
70
XB <=70 (спрос на А)
60
50
Е
40
Пространство
решений
30
20
XB >=0
10
10
XB
10
20
30
40
50
60
70
80
0,3XA + 0,5XB <=20
Ресурс C
0,4XA + 0,3XB <=23
Ресурс D

7.

На сколько можно увеличить запас некоторого ресурса
(дефицитного) для улучшения значения целевой функции Z?
• Как видим из графика, новой точкой оптимума целевой функции
является точка Е
• на сколько необходимо увеличить запас сырья С ?
для этого сначала находим координаты точки Е, решая систему из
двух уравнений, пересечение прямых которых образуют точку Е,
Ха=37,14, Хв=27,14
затем подставляем их в ограничение по сырью С
0,3х37,14 + 0,5х27,14 = 24,71
• В точке Е значения запаса сырья С составляет 24,71 тонн

8.

На сколько можно увеличить запас некоторого ресурса
(дефицитного) для улучшения значения целевой функции Z?
Как видим прирост сырья С составляет 4,71 тонны
При этом прирост доходности составляет 16 980 сом
При этом прирост каждой единицы (тонны) сырья С способствует
приросту дохода предприятия на 3500 сом
При анализе чувствительности оптимального решения на
изменения ограничений, накладываемых на ресурсы, мера
чувствительности решения называется стоимостью единицы
ресурса
В нашем примере стоимость единицы ресурса равна 3500 сом

9.

На сколько можно снизить запас некоторого ресурса
(недефицитного) при сохранении полученного значения целевой
функции Z?
• В нашем примере избыточным ресурсом является сырье Д и
спрос на продукцию А
• Из графика видно, что не изменяя оптимальное решение
величину спроса на продукцию А можно до уровня,
соответствующей точке С
• Также не изменяя оптимальное решение можно уменьшить
запасы сырья Д до величины, соответствующей точке С

10.

На сколько можно снизить запас некоторого ресурса
(недефицитного) при сохранении полученного значения
целевой функции Z?
XA
XA - XB <=10 (спрос на B)
XA >=0
70
XB <=70 (спрос на А)
60
50
Пространство
решений
40
30
С
20
XB >=0
10
10
XB
10
20
30
40
50
60
70
80
0,3XA + 0,5XB <=20
Ресурс C
0,4XA + 0,3XB <=23
Ресурс D

11.

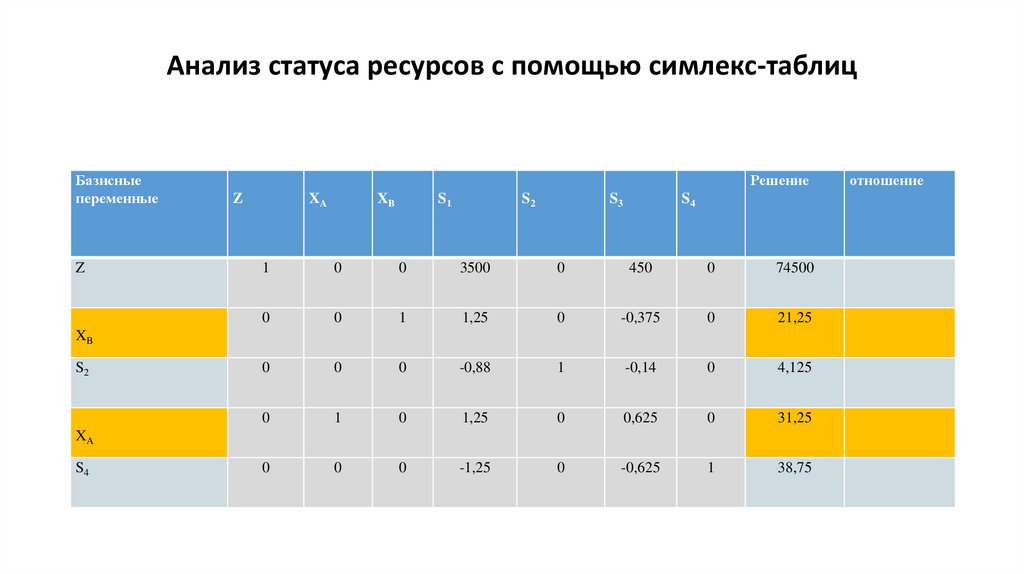
Анализ статуса ресурсов с помощью симлекс-таблиц
Базисные
переменные
Z
Решение
Z
XA
XB
S1
S2
S3
S4
1
0
0
3500
0
450
0
74500
0
0
1
1,25
0
-0,375
0
21,25
0
0
0
-0,88
1
-0,14
0
4,125
0
1
0
1,25
0
0,625
0
31,25
0
0
0
-1,25
0
-0,625
1
38,75
XB
S2
XA
S4
отношение

12.

Анализ статуса ресурсов с помощью симлекс-таблицы
• Как видим из результирующей симплекс-таблицы:
• остаточные переменные S₁ (сырье С) и S₃ (превышение спроса
изделия А относительно изделия В) равны нулю, а это означает
что их статус дефецитный
• Остаточные переменные S₂ (сырье Д) и S₄ (спрос на изделие А)
положительны, что указывает на их недефицитность

13.

Анализ ценности ресурсов с помощью симлекс-таблицы
• Ценность ресурса характеризуется величиной увеличения
целевой функции Z за единицу прироста данного ресурса
• Анализ статуса ресурсов показал, что в нашем примере
дефицитными ресурсами являются сырье С и соотношение
спроса изделий А и В
• Если обратить внимание на значения коэффициентов остаточных
переменных в Z -уравнении, то видим что значения
недефицитных ресурсов (S₂ и S₄) равны нулю, т.е. их увеличение
не дают прироста целевой функции
• Ценность сырья С составляет 3500 сом (что было отмечено и при
анализе чувствительности модели при графическом методе)

14.

В каких пределах допустимо изменение коэффициентов
целевой функции?
• В общем виде целевая функция ЗЛП имеет вид
Z= C₁ X₁ + C₂X₂ → max (min)
• Изменение коэффициентов C₁ и C₂ приводит к изменению угла наклона
прямой Z
• Графический метод решения ЗЛП наглядно показывает, что изменение
угла наклона Z может привести к изменению оптимального решения,
т.е. оно будет соответствовать другой угловой точке пространства
допустимых решений
• Исследование модели на чувствительность целевой функции состоит в
определении интервала изменений ее коэффициентов (C₁ и C₂ ) , в
пределах которых
целевая функция остается неизменной, т.е.
оптимальное решение сохраняется.

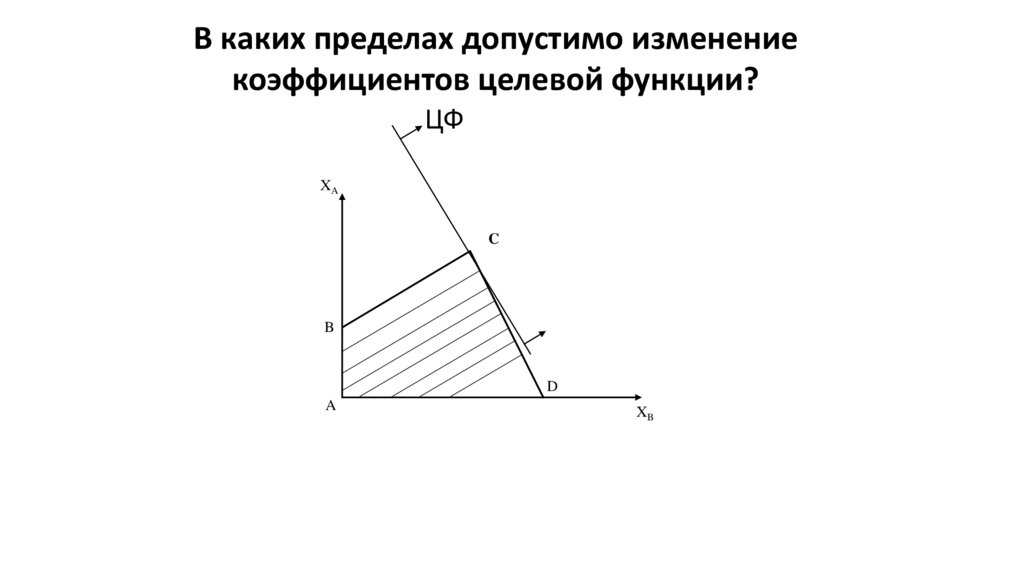
15.

В каких пределах допустимо изменение
коэффициентов целевой функции?
ЦФ
XA
C
B
D
A
XB

16.

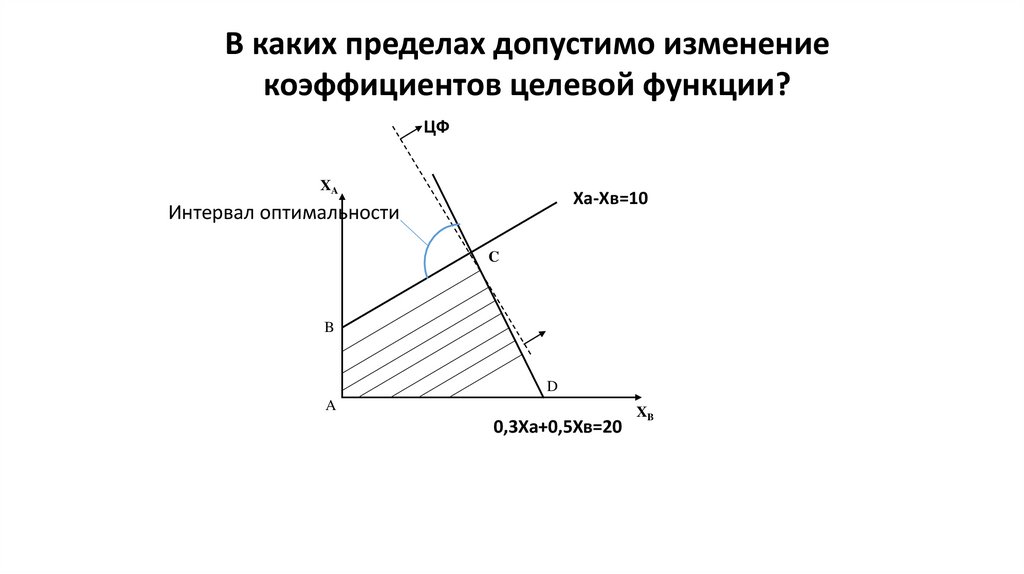
В каких пределах допустимо изменение коэффициентов
целевой функции?
• Для нашего примера ЦФ имеет вид Z= 1500Xа+1300Хв →max
и достигает максимума в точке С.
• При изменении коэффициентов ЦФ точка С останется
соответствующей оптимальному решению до тех пор, пока угол
наклона линии Z будет лежать между прямыми Xа-Хв =10
(ограничение по спросу) и 0.3Xа + 0.5Хв =20 (ограничение по сырью
С), пересечением которых является точка С.

17.

В каких пределах допустимо изменение
коэффициентов целевой функции?
ЦФ
XA
Ха-Хв=10
Интервал оптимальности
C
B
D
A
0,3Ха+0,5Хв=20
XB