Решение систем нелинейных уравнений. Лекция 3

1. ЛЕКЦИЯ 3

Решение систем
нелинейных
уравнений

2.

1. Система нелинейных уравнений
имеет общий вид:
f 1 ( x 1 , x 2 ,..., x n ) 0
f ( x , x ,..., x ) 0
2
1
2
n
..............................
f n ( x 1 , x 2 ,..., x n ) 0
(1)

3.

2. Рассмотрим методы решения (1)
на примере системы из двух
уравнений:
f1 ( x 1 , x 2 ) 0
f
(
x
,
x
)
0
2 1 2
(2)

4.

3. Метод простой итерации
Представим (2) в виде:
x1 g1 ( x1, x 2 )
x 2 g 2 ( x1, x 2 )
(3)

5.

4. или в матричном виде:
x=g(x)
x1
где
x
x
2
g1 ( x 1 , x 2 )
g( x )
g 2 (x1 , x 2 )
(4)
(5)

6.

5. Решением системы (2), (3) или
(4) является вектор
1
x
2
который будучи подставлен в (2) или
в (3) обращает их в равенства.

7.

6. Итерационная формула решения
методом простой итерации имеет вид:
x
g
(
x
)
k
1
k
k=0,1,2,..
или
(6)
x1k 1 g1( x1k , x 2 k )
x 2 k 1 g 2( x1k , x 2 k )
(7)

8.

7. В результате получается
последовательность векторов:
x1k
X k
x
2
k
(8)

9. Если ||J(x)||<1, то итерационный процесс сходится.

8. Погрешность метода простой
итерации зависит от нормы матрицы
и нормы Якобиана
g1
x1
J( x )
g 2
x1
g1
x 2
g 2
x 2
(9)
Если ||J(x)||<1, то
итерационный процесс сходится.

10.

9. Опишем способ преобразования
уравнений(2) к виду (3).
Представим правые части уравнений
(3) в виде:
g1(x1, x 2) x1 11 f 1(x1, x 2) 12 f 2(x1, x 2)
g2(x1, x 2) x 2 21 f 1(x1, x 2) 22 f 2(x1, x 2)
(10)

11.

10. Для вычисления ( ij)
используют условие, что в
начальной точке x0 норма
||J(x)||=0, то есть сама матрица
Якоби (9) приравнивается к нулю.
J(x0)=0

12.

11. То есть:
g1
0
x1 X 0
g1
0
x 2 X 0
g 2
0
x1 X 0
g 2
0
x 2 X 0
(11)

13.

12. Из (10) с учетом (11) получим
систему:
f 1
f 2
1 11 x1 12 x1 0
X0
X0
f 1
f 2
11
12
0
x 2 X 0
x 2 X 0
f 1 f 2 0
22
21 x1 X
x1 X 0
0
f 1
f 2
1
0
21
22
x 2 X 0
x 2 X 0
(12)

14.

13. Из (12) можно найти
неизвестные ( ij):
11
1
1
J ( x 0 )
0
12
21
0
1
J ( x 0 )
1
12
(13)

15.

14. Где:
g1
x1 X 0
J x 0
g 2
x1 X 0
g1
x 2 X 0
g 2
x 2 X 0

16.

15. Итерационная формула метода
простой итерации примет вид:
x1k 1 x1k 11 f 1( x1k , x2 k ) 12 f 2( x1k , x2 k )
x2 k 1 x2 k 21 f 1( x1k , x2 k ) 22 f 2( x1k , x2 k )
(14)
Или в матричной форме получим
x1k 1
x1k 11 12 f 1( x1k , x 2 k )
x 2 k 1 x 2 k 21 22 f 2( x1k , x 2 k )

17.

16. Метод Ньютона
Запишем (1) в матричном виде:
f1 ( x 1 , x 2 ,..., x n )
f 2 ( x 1 , x 2 ,..., x n )
F( x )
0
.........................
f n ( x 1 , x 2 ,..., x n )
(15)

18.

17. Пусть x10, x20,…,xn0 –
начальные приближения.
x10
x20
X0
...
xn 0

19.

18. Заменим каждое из нелинейных
уравнений (15) линейным, полученным
разложением в ряд Тейлора. Например,
первое уравнение после линеаризации
будет иметь вид:
f 1( x10 , x 20 ,..., xn0 )
f 1( x10 , x 20 ,..., xn0 )
( x1 x10 )
x1
(16)
f 1( x10 , x 20 ,..., xn0 )
( x 2 x 20 ) ...
x 2
f 1( x10 , x 20 ,..., xn0 )
( xn xn0 )
xn

20.

19. Запишем матрицу Якоби, то есть
матрицу производных:
f 1
x1
f 2
J ( x ) x1
fn
x1
f 1
f 1
...
x 2
xn
f 2
f 2
...
x 2
xn
fn
fn
...
x 2
xn
(17)

21.

20. Тогда систему линеаризованных
уравнений можно записать в
матричном виде:
F(X 0 )
F(X 0 )
(X X 0 ) 0
X
(18)
Эта система линейна относительно
поправок xk,1=xk,1-xk,0

22.

21. Если матрица Якоби не
вырождена, то можно найти
поправки и первое
приближение
X1=X0+ X1
(19)

23.

22. Каждый шаг итерационного
процесса состоит из решения
линейной системы
F ( X i )
X i 1 F ( X i )
X
(20)
и определения следующего приближения
неизвестных
(21)
Xi+1=Xi+ Xi+1

24.

23. Или итерационный процесс в
матричной форме:
F(X i )
X i 1 X i
F(X i )
X
(22)

25.

24. Конец итерации наступает при
обеспечении заданной точности
X i 1 X i

26.

25. Использование встроенных в
MathCad функций.
Для решения систем нелинейных
уравнений в MathCad
используется блок Given-Find.

27.

26. Использование блока Given-Find имеет
стандартную последовательность:
- задаются функции f1(x), f2(x), …, fn(x)
- если необходимо строятся графики
- задаются начальные приближения
неизвестным переменным x1:=x10
x2:= x20
… xn=xn0
служебное слово Given
блок нелинейных уравнений записывается через
булевое равно (=)
находится решение с помощью встроенной
функции Find
Find(x1,x2,…xn)=

28.

27. Задание 1.
Решение системы нелинейных
уравнений методом простой итерации.
Система двух нелинейных уравнений
f1 ( x1 x2 )
x2 x1
f2 ( x1 x2 )
2
( x1 )
x2
1
( x2 )
2
1
x1:=1.5 x2:=1.5 – начальные приближения

29.

28. Вычислим Якобиан А:
A11
d
f1 ( x1 x2 )
d x1
A21
d
f1 ( x1 x2 )
d x2
A
A11 A12
A21 A22
A12
d
f2 ( x1 x2 )
d x1
A22
d
f2 ( x1 x2 )
d x2

30.

29. Вычисляем вспомогательные
коэффициенты L11, L12, L21, L22
L11
L12
A
1
1
L21
0
L22
A
1
0
1

31.

30. Итерационные формулы
k:=1..10
xx11 1.5
:
xx 2 1.5
1
- начальные приближения

32.

31. итерации:
xx1k
xx2k
1
xx1k
L11 L12
1
xx2k
L21 L22
f1 xx1k xx2k
f2 xx1k xx2k

33.

32. Результат:
xx1k
xx2k
1.5
1.5
1.708
1.375
1.719
1.395
1.717
1.396
1.717
1.395
1.717
1.395
1.717
1.395
1.717
1.395
1.717
1.395
1.717
1.395
Корни х1=1.717 и х2=1.395
совпали
с корнями
при помощи
всроенной
ф
Корни
х1=1.717
и х2=1.395найденными
совпали с корнями
найденными
при помощ
Корни х1=1.717 и х2=1.395 совпали с корнями
найденными при помощи встроенной функции Given
– Find.

34.

33. Задание 2.
Решение системы нелинейных
уравнений с помощью блока
Given-Find.

35.

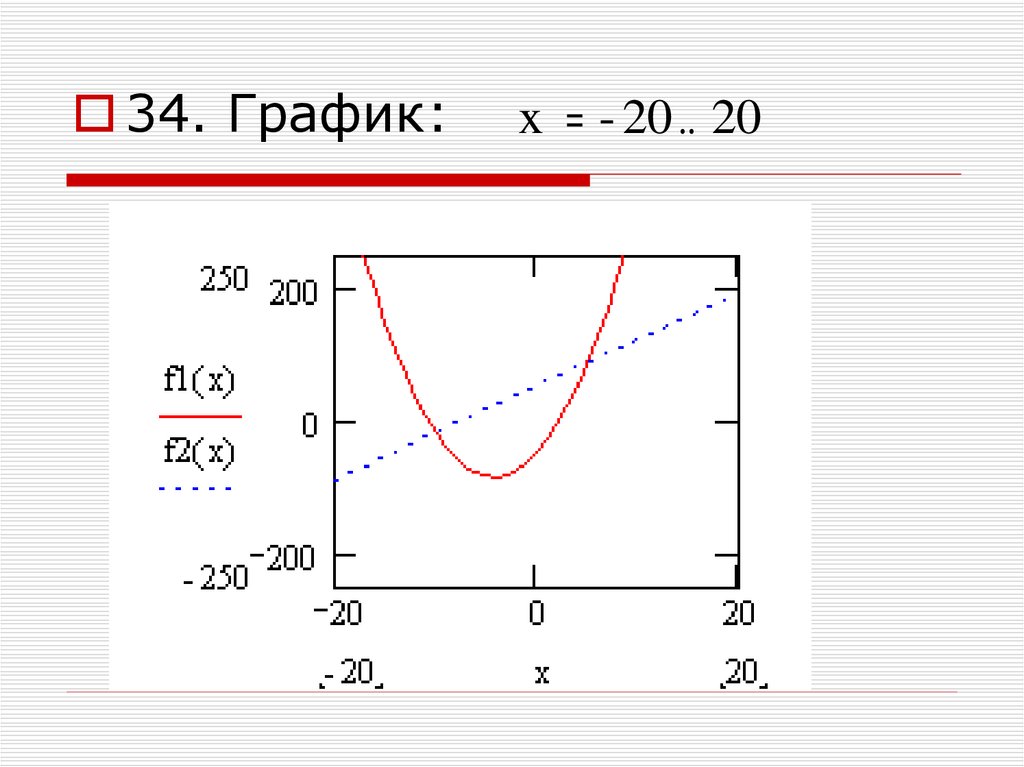
34. С одной неизвестной:
f1 ( x)
f2 ( x)
2
2x
17 x 50
7 x 50

36.

34. График:
x
20 20

37.

35. 1-й корень
Given
x
10
y
y f1 ( x)
y f2 ( x)
x1
y1
0
Find ( x y)
x1 10 y1 20

38.

36. 2-й корень
x
10 y 100
Given
y f1 ( x)
x2
y2
y f2 ( x)
Find ( x y)
x2 5
y2 85

39.

37.С двумя неизвестными
F1 ( x1 x2 )
x2 x1
x2
F2 ( x1 x2 )
2
2
x1
x2
1
1

40.

38. 1-й корень
x1:=1,5 x2:=1,5 z:=0
Given
Given
z
F2 ( x1 x2 )
z
F1 ( x1 x2 )
x1
x2
x1=1.717
Find ( x1 x2 )
x2=1.395
8
8
8
F1 (F1
x1 ( x2
)
5.139
10
x1 x2) 5.139 10
F2 ( x1 x2) 4.392 10

41.

39. 2-й корень
x1:=1.5 x2:=1.5
Given
F2 ( x1 x2) z
z
x1
x2
F1 ( x1 x2)
Find ( x1 x2 )
x1 1.107
x2 0.475