Похожие презентации:
Динамика. Лекция 3
1.
Кафедра физикиМЕХАНИЧЕСКАЯ
ЭНЕРГИЯ
Энергией называется физическая величина, являющаяся общей
количественной мерой движения и взаимодействия всех видов
материи.
Механическая энергия - физическая величина, характеризующая
способность тела совершать механическую работу.
К механическим видам энергии относятся
потенциальная энергии.
кинетическая
и
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ.
Запишем уравнение движения (второй закон Ньютона)
dv
m
F
для механической системы из одной частицы
dt
результирующая
сил,
действующих
на
частицу.
F
Общая физика «Основы классической механики»
1
2.
Кафедра физикиРАБОТА
Если на частицу действует сила F , кинетическая энергия частицы
изменяется:
2
mv
(Fds )
d
2
В этом случае приращение кинетической
энергии частицы за время dt
равно скалярному произведению (Fds ).
Величина dA (Fds ) называется работой, совершаемой силой F на
пути d. s .
Работа – это физическая величина, равная произведению силы на
путь, пройденный телом под действием этой силы.
Работа характеризует изменение
действием силы на движущуюся
совершает только сила.
Общая физика «Основы классической механики»
энергии, обусловленное
частицу. Иначе, работу
2
3.
Кафедра физикиРАБОТА
Проинтегрируем соотношение
mv 2
Fs ds
d
2
вдоль траектории от точки 1 до точки 2:
mv 2
Fs ds
d
2
1
1
2
2
2
2
mv 2
mv1
Fs ds
2
2
1
2
Иначе: K 2 K 1 A
2
Fs ds - работа силы F на пути 1–2.
1
Работа результирующей всех сил, действующих на частицу, идет на
приращение кинетической энергии частицы.
Общая физика «Основы классической механики»
3
4.
Кафедра физикиПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Потенциальной называется часть механической энергии системы,
зависящей от взаимного расположения тел, составляющих эту
систему, и от их положения во внешнем силовом поле.
Дать более точное представление о потенциальной энергии проще
через взаимосвязь энергии с работой определенного типа сил.
Оказывается, что само понятие потенциальной энергии применимо
лишь для сил, которые носят название консервативные силы.
Работа консервативных сил по перемещению тела по замкнутой
траектории всегда равна нулю.
Общая физика «Основы классической механики»
4
5.
Кафедра физикиПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Оказывается, что все 4 типа фундаментальных сил консервативные.
Пример неконсервативных сил: трение. Работа таких сил может
приводить к выделению тепла (диссипации энергии).
A12 W p 2 W p 1 W p 1 W p 2
Работа консервативной силы А12 равна изменению потенциальной
энергии частицы, взятому с обратным знаком.
Общая физика «Основы классической механики»
5
6.
Кафедра физикиЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Пусть на частицу кроме консервативных сил действует также
неконсервативная сила F *. Тогда при переходе частицы из точки
1 в точку 2 будет совершаться работа
2
*
*
A12 Fds F ds Aконсерв A12
1
*
A12
- работа неконсервативной силы.
Работу консервативных сил представим как
*
Тогда
A12 W p1 W p2 A12
Aконсерв W p 1 W p 2
Работа результирующей сил, действующих на частицу, идет на
приращение кинетической энергии частицы, т.е.
A12 K 2 K 1
Общая физика «Основы классической механики»
6
7.
Кафедра физикиЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
В итоге получим:
*
K 2 K 1 W p 1 W p 2 A12
K W E
*
K 2 W p 2 K 1 W p 1 A12
- полная механическая энергия частицы
*
E 2 E1 A12
Изменение полной механической энергии частицы, находящейся
в поле консервативных сил, равно работе неконсервативных сил,
действующих на частицу
Полная механическая энергия системы невзаимодействующих
частиц, на которые действуют только консервативные силы,
остается постоянной.
Это закон сохранения полной механической энергии.
Общая физика «Основы классической механики»
7
8.
Кафедра физикиЗАКОНЫ СОХРАНЕНИЯ. Пример практического применения
Абсолютно упругий центральный удар
m1
m2
v1
v2
Массы шаров и их скорости до
соударения известны. Шары
однородны.
Задача: рассмотреть абсолютно упругий удар шаров. Определить
параметры механического движения шаров после соударения,
выполнить анализ.
Абсолютно упругим называется такой удар, при котором
механическая энергия тел не переходит в другие, немеханические,
виды энергии.
Абсолютно неупругий удар - кинетическая энергия тел частично
или полностью превращается во внутреннюю энергию; после удара
столкнувшиеся тела движутся с одинаковой скоростью, либо
покоятся.
Общая физика «Основы классической механики»
8
9.
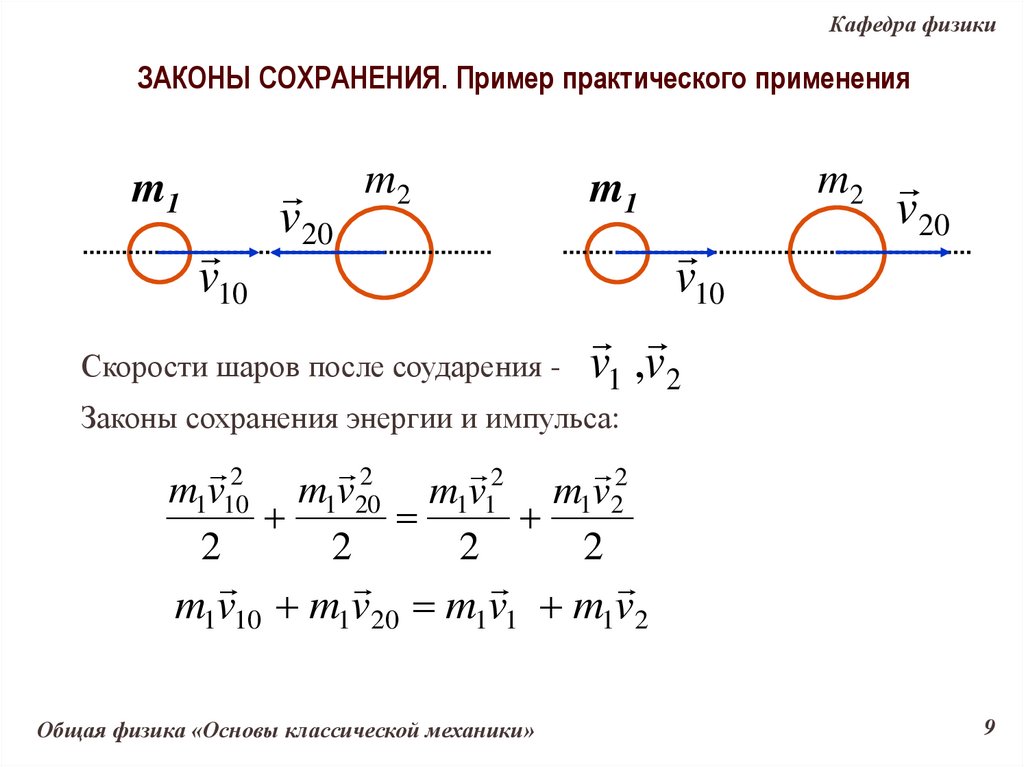
Кафедра физикиЗАКОНЫ СОХРАНЕНИЯ. Пример практического применения
m1
v10
m2
v20
m2
m1
v10
v20
Скорости шаров после соударения - v1 ,v 2
Законы сохранения энергии и импульса:
2
2
2
2
m1v10 m1v20 m1v1 m1v2
2
2
2
2
m1v10 m1v20 m1v1 m1v2
Общая физика «Основы классической механики»
9
10.
Кафедра физикиЗАКОНЫ СОХРАНЕНИЯ. Пример практического применения
Преобразуем выражение ( a 2 b 2 a b a b ):
m1 v10 v1 v10 v1 m2 v2 v20 v2 v20
После преобразований:
m1 v10 v1 m2 v2 v20
Скорости шаров до после удара будут направлены вдоль одной
прямой, следовательно, векторы в полученных соотношениях
коллинеарные (направлены вдоль параллельных прямых).
Правило для коллинеарных векторов a , b , c :
Если ab ac , то b c
Общая физика «Основы классической механики»
10
11.
Кафедра физикиЗАКОНЫ СОХРАНЕНИЯ. Пример практического применения
После преобразований получим:
2m2 v20 m1 m2 v10
v1
m1 m2
2m1v10 m2 m1 v20
v2
m1 m2
Общая физика «Основы классической механики»
11
12.
Кафедра физикиЛЕКЦИЯ 3
Динамика
План лекции
1. Динамика вращательного движения твердого тела:
моменты импульса и силы;
момент инерции тела. Теорема Штейнера.
2. Закон сохранения момента импульса.
Пример применения закона сохранения момента импульса.
Общая физика. Раздел "Основы классической механики"
12
13.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
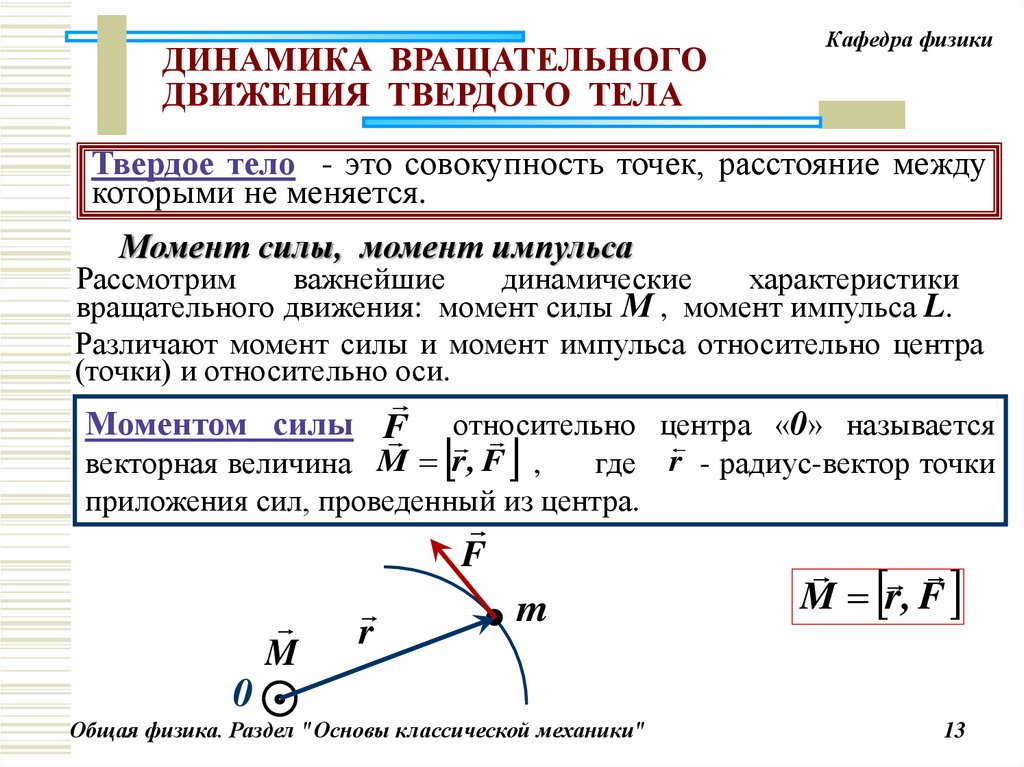
Твердое тело - это совокупность точек, расстояние между
которыми не меняется.
Момент силы, момент импульса
Рассмотрим
важнейшие
динамические
характеристики
вращательного движения: момент силы М , момент импульса L.
Различают момент силы и момент импульса относительно центра
(точки) и относительно оси.
Моментом силы F
относительно
центра «0» называется
r
M
r
,
F
векторная величина
,
где
- радиус-вектор точки
приложения сил, проведенный из центра.
F
M
r
m
M r , F
0
Общая физика. Раздел "Основы классической механики"
13
14.
Кафедра физикиДИНАМИКА ВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Момент силы, момент импульса
Момент силы характеризует способность
вращение тела и изменять угловую скорость.
силы
вызывать
Момент импульса
относительно центра «0» - это векторная
L
величина L r , p .
L
0
m
r
p
L r , p
Момент импульса в динамике играет ту же роль, что и импульс в
поступательном движении.
Общая физика. Раздел "Основы классической механики"
14
15.
ЗАКОН СОХРАНЕНИЯ МОМЕНТАИМПУЛЬСА
Кафедра физики
Суммарный момент импульса
L системы частиц связан с
суммарным моментом M внешних сил, действующих на
систему, уравнением моментов:
d L dt M
второй закон Ньютона, записанный
для моментов импульсов и сил.
M M1 M2 Mi Mi
i
L L1 L2 Li Li
i 1, 2 , n
i
Момент импульса системы, как и импульс, является
величиной аддитивной.
Общая физика. Раздел "Основы классической механики"
15
16.
ЗАКОН СОХРАНЕНИЯ МОМЕНТАИМПУЛЬСА
Если в d L dt M
Кафедра физики
положить M равным нулю, получим:
d L dt 0
Момент импульса замкнутой системы
материальных точек остается постоянным
Общая физика. Раздел "Основы классической механики"
16
17.
ЗАКОН СОХРАНЕНИЯ МОМЕНТАИМПУЛЬСА
Кафедра физики
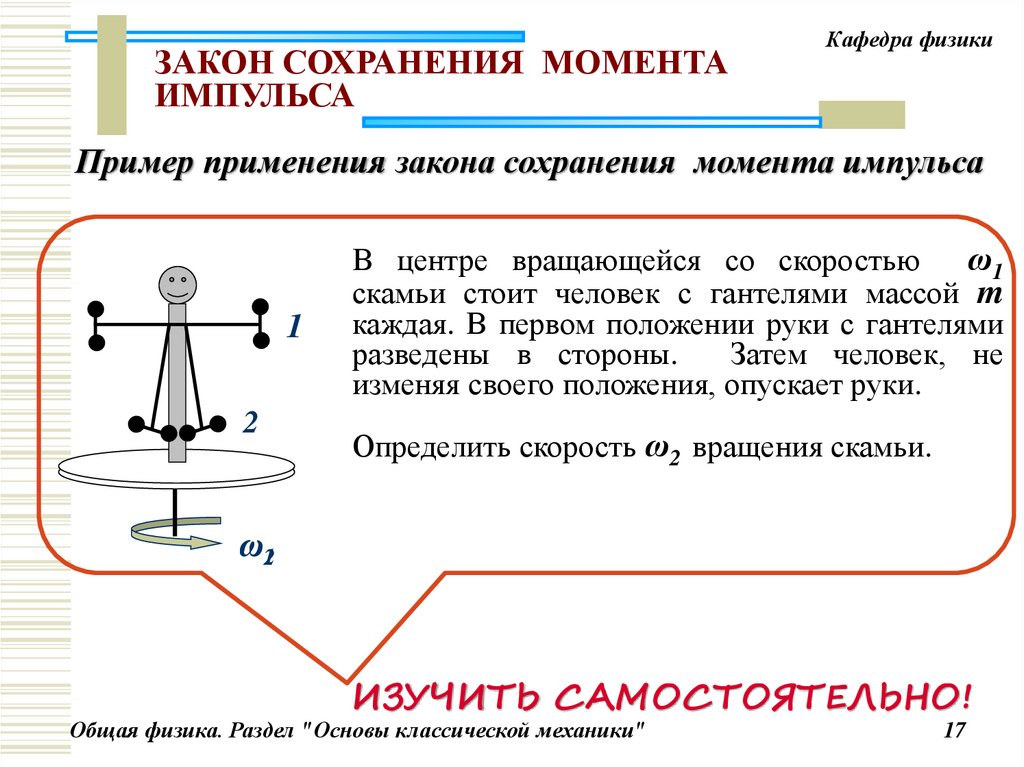
Пример применения закона сохранения момента импульса
1
2
В центре вращающейся со скоростью
ω1
скамьи стоит человек с гантелями массой m
каждая. В первом положении руки с гантелями
разведены в стороны.
Затем человек, не
изменяя своего положения, опускает руки.
Определить скорость ω2 вращения скамьи.
ω21
ИЗУЧИТЬ САМОСТОЯТЕЛЬНО!
Общая физика. Раздел "Основы классической механики"
17
18.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
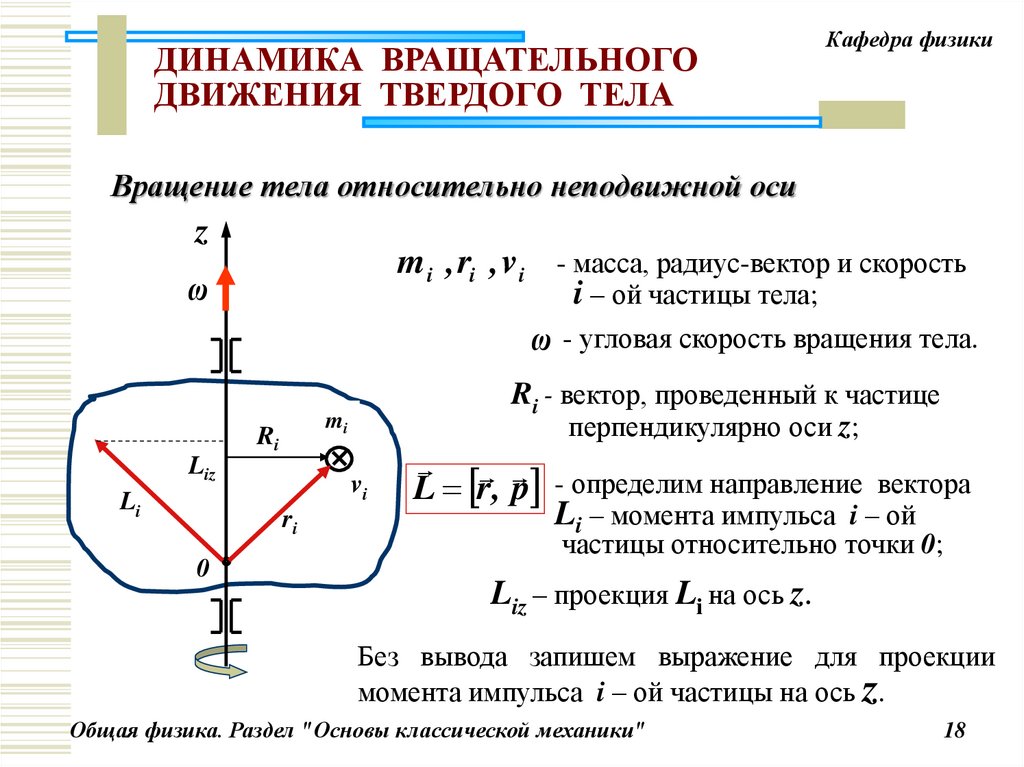
Вращение тела относительно неподвижной оси
z
m i , ri , v i - масса, радиус-вектор и скорость
i – ой частицы тела;
ω - угловая скорость вращения тела.
ω
mi
Ri
Liz
Li
vi
ri
0
Ri - вектор, проведенный к частице
перпендикулярно оси z;
L r, p - определим направление вектора
Li – момента импульса i – ой
частицы относительно точки 0;
Liz – проекция Li на ось z.
Без вывода запишем выражение для проекции
момента импульса i – ой частицы на ось z.
Общая физика. Раздел "Основы классической механики"
18
19.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
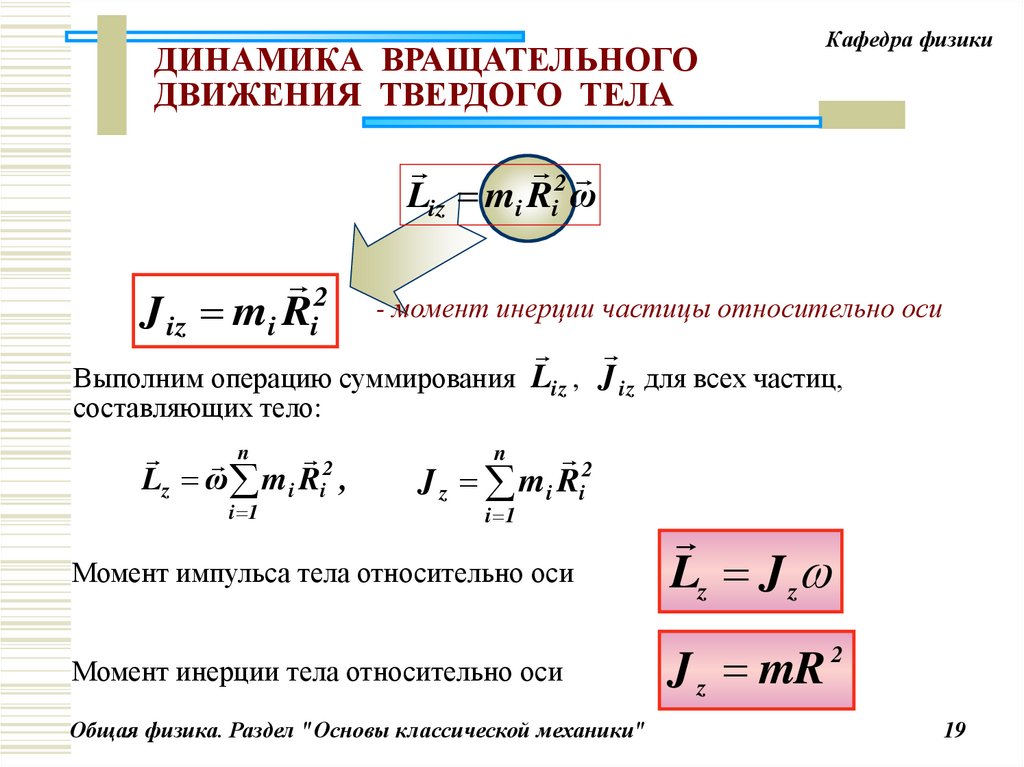
2
Liz mi Ri ω
2
J iz mi Ri
- момент инерции частицы относительно оси
Выполним операцию суммирования Liz , J iz для всех частиц,
составляющих тело:
2
n
Lz ω m i Ri ,
i 1
2
J z m i Ri
n
i 1
Момент импульса тела относительно оси
Момент инерции тела относительно оси
Общая физика. Раздел "Основы классической механики"
Lz J z
J z mR 2
19
20.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
Момент инерции
Формулы для вычисления моментов инерции для стандартных тел
Тело
Ориентация оси
Момент инерции
Полый тонкостенный цилиндр с По оси цилиндра
радиусом R и массой m
mR 2
Сплошной цилиндр с радиусом
R и массой m
m 2
R
2
По оси цилиндра
Полый тонкостенный цилиндр с По оси цилиндра
радиусом
с
внутренним
радиусом R1, внешним радиусом
R2 и массой m
Диск с радиусом R и массой m
По оси диска
Общая физика. Раздел "Основы классической механики"
m 2
R1 R22
2
m 2
R
2
20
21.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
Теорема Штейнера.
ИЗУЧИТЬ САМОСТОЯТЕЛЬНО!
Общая физика. Раздел "Основы классической механики"
21
22.
Кафедра физикиДИНАМИКА ВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
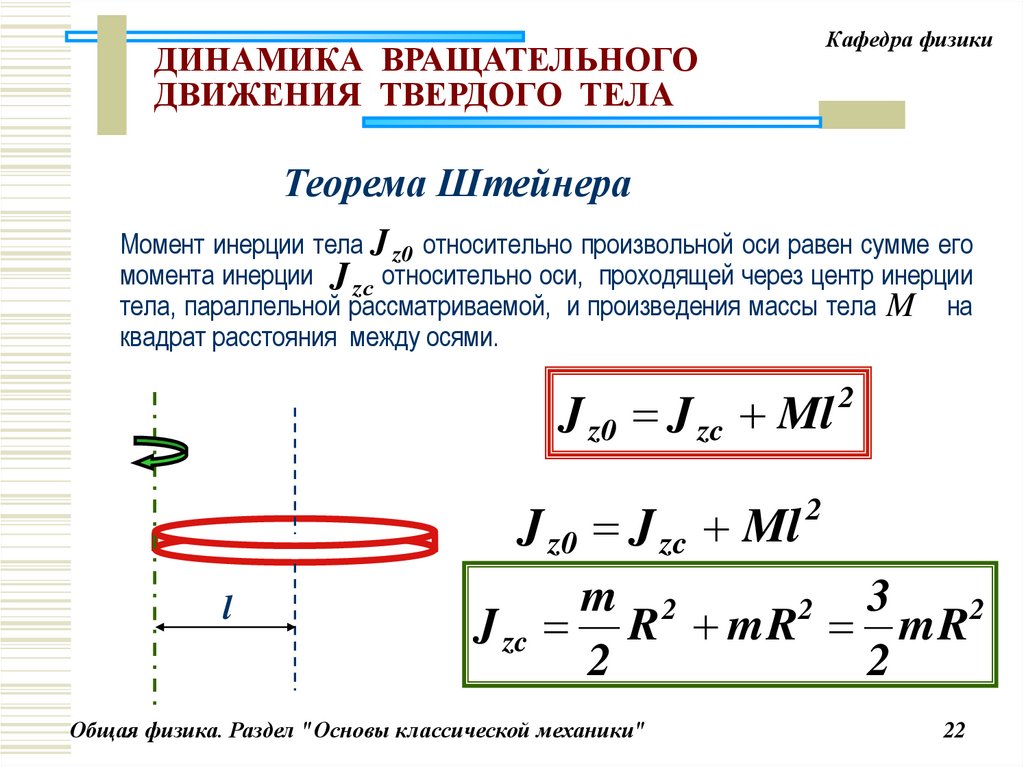
Теорема Штейнера
Момент инерции тела J z0 относительно произвольной оси равен сумме его
момента инерции J zс относительно оси, проходящей через центр инерции
тела, параллельной рассматриваемой, и произведения массы тела M на
квадрат расстояния между осями.
J z0 J zc Ml
2
J z0 J zc Ml
m 2
3
2
2
J zc R mR mR
2
2
2
l
Общая физика. Раздел "Основы классической механики"
22
















 Физика
Физика








