Похожие презентации:
Динаамика. Вращательное движение. Энергия. (Лекция 3)
1.
Кафедра физикиЛЕКЦИЯ 3
План лекции
1.
2.
3.
4.
5.
6.
Динамика
Динамика вращательного движения твердого тела
Закон сохранения момента импульса
Неинерциальные системы отсчета. Силы инерции
Кинетическая энергия, работа, мощность
Потенциальная энергия
Закон сохранения механической энергии
Общая физика. Раздел "Основы классической механики"
1
2.
Кафедра физикиДИНАМИКА ВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Момент силы, момент импульса
Твердое тело - совокупность точек, расстояние между которыми
не меняется.
Важные динамические характеристики вращательного
движения:
F
момент силы М, момент импульса L.
Различают момент силы
и
момент
импульса
относительно
центра
(точки) и относительно
оси.
Моментом силы F
M
r
m
M r, F
0
относительно
центра
«0» называется
векторная величина M r , F ,
где r - радиус-вектор точки
приложения сил, проведенный из центра.
Момент силы характеризует способность
вращение тела и изменять угловую скорость.
Общая физика. Раздел "Основы классической механики"
силы
вызывать
2
3.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
Момент силы, момент импульса
Момент импульса
L относительно центра «0» - это векторная
величина L r , p .
L
0
L r , p
m
r
p
Момент импульса в динамике играет ту же роль, что и импульс в
поступательном движении.
Общая физика. Раздел "Основы классической механики"
3
4.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
Плечо импульса и силы относительно точки
l = r sin -
плечо импульса
относительно точки «0».
L l=r sin
0
α
r
m
р
α
Модуль вектора момента импульса
частицы относительно точки «0»
равен:
L p r sin pl
По аналогии модуль вектора момента силы частицы относительно
точки «0» равен:
M F r sin Fl
Общая физика. Раздел "Основы классической механики"
4
5.
Кафедра физикиДИНАМИКА ВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Вращение твердого тела относительно оси
Момент инерции
Момент импульса тела относительно оси
Jz
Lz J z
- момент инерции тела относительно оси (аналог массы).
Момент инерции материальной точки массой m,
вращающейся
относительно оси вращения по
окружности радиуса R, равен
J z mR 2
Момент инерции тела массой m , вращающейся относительно оси
вращения по окружности радиуса R , равен
n
Jz
n
m i Ri2
m
i 1
Общая физика. Раздел "Основы классической механики"
m
i
i 1
5
6.
Кафедра физикиДИНАМИКА ВРАЩАТЕЛЬНОГО
ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Момент инерции
Формулы для вычисления моментов инерции для стандартных тел
рассмотреть самостоятельно
Тело
Ориентация оси
Момент инерции
Полый тонкостенный цилиндр с По оси цилиндра
радиусом R и массой m
mR 2
Сплошной цилиндр с радиусом
R и массой m
m 2
R
2
По оси цилиндра
Полый тонкостенный цилиндр с По оси цилиндра
радиусом
с
внутренним
радиусом R1, внешним радиусом
R2 и массой m
Диск с радиусом R и массой m
По оси диска
Общая физика. Раздел "Основы классической механики"
m 2
R1 R22
2
m 2
R
2
6
7.
ДИНАМИКА ВРАЩАТЕЛЬНОГОДВИЖЕНИЯ ТВЕРДОГО ТЕЛА
Кафедра физики
Момент инерции. Теорема Штейнера.
Момент инерции тела
Штейнера –
относительно произвольной оси. Теорема
изучить
самостоятельно
Общая физика. Раздел "Основы классической механики"
7
8.
Кафедра физикиЗАКОН СОХРАНЕНИЯ МОМЕНТА
ИМПУЛЬСА
L системы частиц связан с
Суммарный момент импульса
суммарным моментом M
внешних сил, действующих на
систему, уравнением моментов:
моментов
d L dt M
второй закон Ньютона, записанный
для моментов импульсов и сил.
M M1 M2 Mi
L L1 L2 Li
i
Mi
Li
i 1, 2, n
i
Общая физика. Раздел "Основы классической механики"
8
9.
Кафедра физикиЗАКОН СОХРАНЕНИЯ МОМЕНТА
ИМПУЛЬСА
Если в
d L dt M
положить M равным нулю, получим:
d L dt 0
Момент импульса замкнутой системы
материальных точек остается постоянным
Общая физика. Раздел "Основы классической механики"
9
10.
Кафедра физикиНЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ
ОТСЧЕТА
но
ль
ть
чи
яте
изу осто
сам
Силы инерции. Центробежные силы инерции. Сила Кориолиса.
Примеры проявления центробежных сил инерции -
Общая физика. Раздел "Основы классической механики"
10
11.
Кафедра физикиКИНЕТИЧЕСКАЯ ЭНЕРГИЯ
Запишем уравнение движения (второй закон Ньютона)
dv
m
F
для механической системы из одной частицы
dt
F - результирующая сил, действующих на частицу.
Умножим уравнение движения на перемещение частицы v dt ds.:
dv
m( v
)dt ( Fds )
dt
m ( v dv ) ( F ds )
Внесем скорость под знак дифференциала, получим:
v2
mv 2
( F ds )
md d
2
2
Общая физика. Раздел "Основы классической механики"
11
12.
Кафедра физикиКИНЕТИЧЕСКАЯ ЭНЕРГИЯ
Если система замкнута, т.е. F 0
следовательно
mv 2
2
2
mv
d
2
0
const T
Эта величина называется кинетической энергией частицы.
Общая физика. Раздел "Основы классической механики"
12
13.
Кафедра физикиРАБОТА
сила F,
Если на частицу действует
кинетическая энергия частицы изменяется:
mv 2
d
2
(Fds )
В этом случае приращение кинетической
энергии частицы за время
равно скалярному произведению(Fds ) .
Величина dA (Fds )
на пути
ds .
записать
dt
называется работой, совершаемой силой
F
Следовательно, раскрыв скалярное произведение, можно
dA Fs ds
Работа – это физическая величина, равная произведению силы на
путь, пройденный телом под действием этой силы.
Работа характеризует изменение энергии, обусловленное действием силы
на движущуюся частицу. Иначе, работу совершает только сила.
Общая физика. Раздел "Основы классической механики"
13
14.
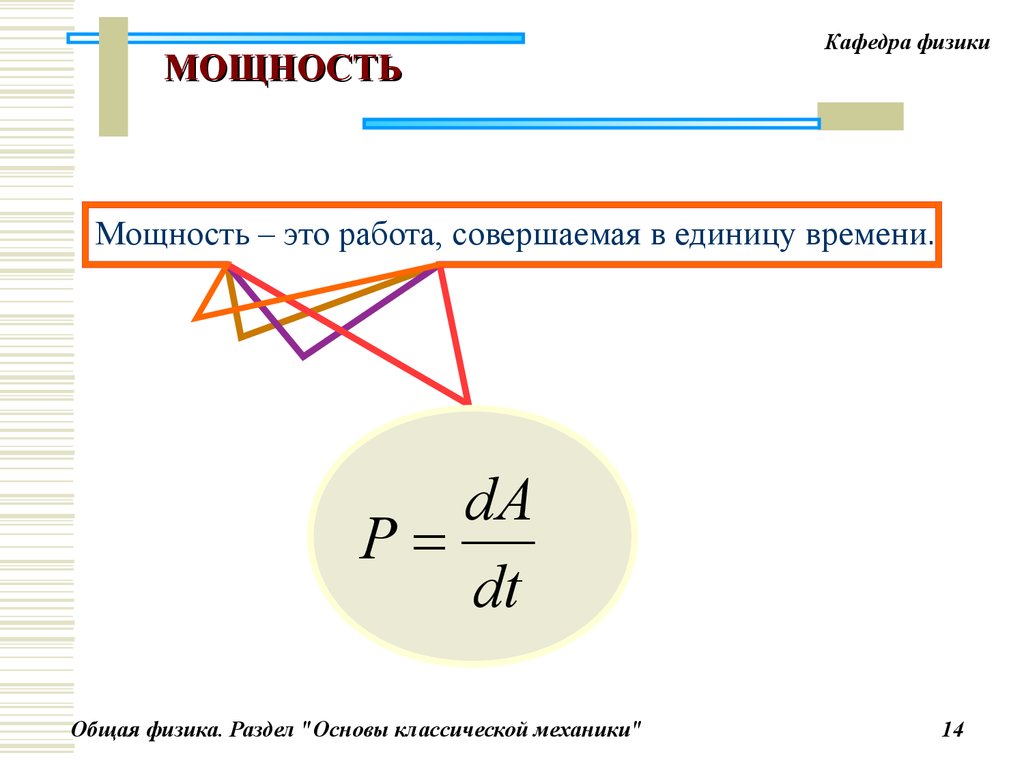
МОЩНОСТЬКафедра физики
Мощность – это работа, совершаемая в единицу времени.
dA
P
dt
Общая физика. Раздел "Основы классической механики"
14
15.
Кафедра физикиПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Силовые поля делятся на потенциальные и непотенциальные
Потенциальным называется такое силовое поле, которое может
быть выражено через некоторую скалярную функцию П (x, y, z, t),
называемую потенциальной, по следующему правилу:
dП dП dП
F
ex
ey
e z
dy
dz
dx
F - сила, действующая на частицу в потенциальном поле
Используем векторную дифференциальную операцию, называемую
градиентом:
dП dП dП
qradП
ex
ey
ez
dx
dy
dz
Общая физика. Раздел "Основы классической механики"
15
16.
Кафедра физикиПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Таким образом, потенциальная сила записывается в виде:
F qradП
Консервативными являются такие потенциальные силовые поля,
которые явно не зависят от времени.
Потенциальная функция П в таком случае называется
потенциальной энергией частицы во внешнем консервативном поле.
Общая физика. Раздел "Основы классической механики"
16
17.
Кафедра физикиПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Пусть W p
потенциальная функция. Тогда
dW p
dW p
dW p
F qrad W p x, y, z
ex
ey
e z
dy
dz
dx
Сила, действующая на движущуюся частицу, совершает работу.
Несложно показать, что для конечных перемещений из точки 1 в точку 2
A12 W p1 W p2
Работа консервативной силы А12
равна изменению
потенциальной энергии частицы, взятому с обратным знаком.
Работа консервативной силы не зависит от того, по какой
траектории перемещается частица из начальной точки в конечную.
Общая физика. Раздел "Основы классической механики"
17
18.
Кафедра физикиЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Рассмотрим систему, состоящую из N не взаимодействующих
между собой частиц, находящихся в поле консервативных сил.
Кинетическая и потенциальная энергии i -ой частицы:
K i m i v i2 2 ,
Wi Wi xi , yi , z i
E i K i W i const
Полная энергия частицы:
N
E
N
N
E K W
i
i 1
i
i 1
i
const
i 1
Полная механическая энергия системы невзаимодействующих
частиц, на которые действуют только консервативные силы,
остается постоянной.
Общая физика. Раздел "Основы классической механики"
18
19.
Кафедра физикиЗАКОНЫ СОХРАНЕНИЯ. Пример практического применения
Абсолютно упругий удар
Абсолютно упругим называется такой удар, при котором
механическая энергия тел не переходит в другие,
немеханические, виды энергии.
Рассмотреть абсолютно упругий удар двух однородных частиц,
образующих замкнутую систему -
самостоятельно
Общая физика. Раздел "Основы классической механики"
19


















 Физика
Физика








