Решение задач с параметрами

1.

Решение задач с
параметрами
Выполнила: Матвиенко Елена
Валентиновна – учитель математики
ГООУ санаторной школы-интерната
г.Петровска Саратовской области.

2.

1. Найти все значения параметра а, х 2 ах 2
2,
2
при которых решением системы
х х 1
2
является вся прямая.
х ах 2 3.
х2 х 1
2. При каких значениях
5
2
параметра р функция
у (4 р) х 5х (1 р)
8
определена при всех хєR ?
3. При каких значениях параметра а
система неравенств
а) имеет единственное решение;
б) не имеет решений;
в) имеет бесконечно много
решений?
х 2 8 х 15 0,
2
х (а 4) х 4а 0.

3.

1. Найти все значения параметра а,
при которых решением системы
является вся прямая.
Решение.
х 2 ах 2
2,
2
х х 1
2
х ах 2 3
х 2 х 1
х 2 ах 2
2,
2
х х 1
2
х ах 2 3.
х 2 х 1
х ах 2 2 х 2 х 2
0,
2
х х 1
2
2
х ах 2 3 х 3 х 3 0
х2 х 1
2
2
х 2 ( а 2) х 4
0,
2
х х 1
2
4 х (а 3) х 1 0.
х2 х 1
Так как квадратный трехчлен х2-х+1=(х2-2·0,5·х+0,25)+0,75= (х-0,5)2+0,75>0
Оцените
знаменатель дробей.
при любом значении х, то получим систему неравенств:
х 2 (а 2) х 4 0,
2
4 х (а 3) х 1 0.

4.

Система
неравенств
имеет решением
числовую
прямую,
Когда система
неравенств
будетвсю
иметь
решением
когда
решение каждого
неравенства этой системы – есть вся
всю числовую
прямую?
числовая прямая.
х 2 (а 2) х 4 0,
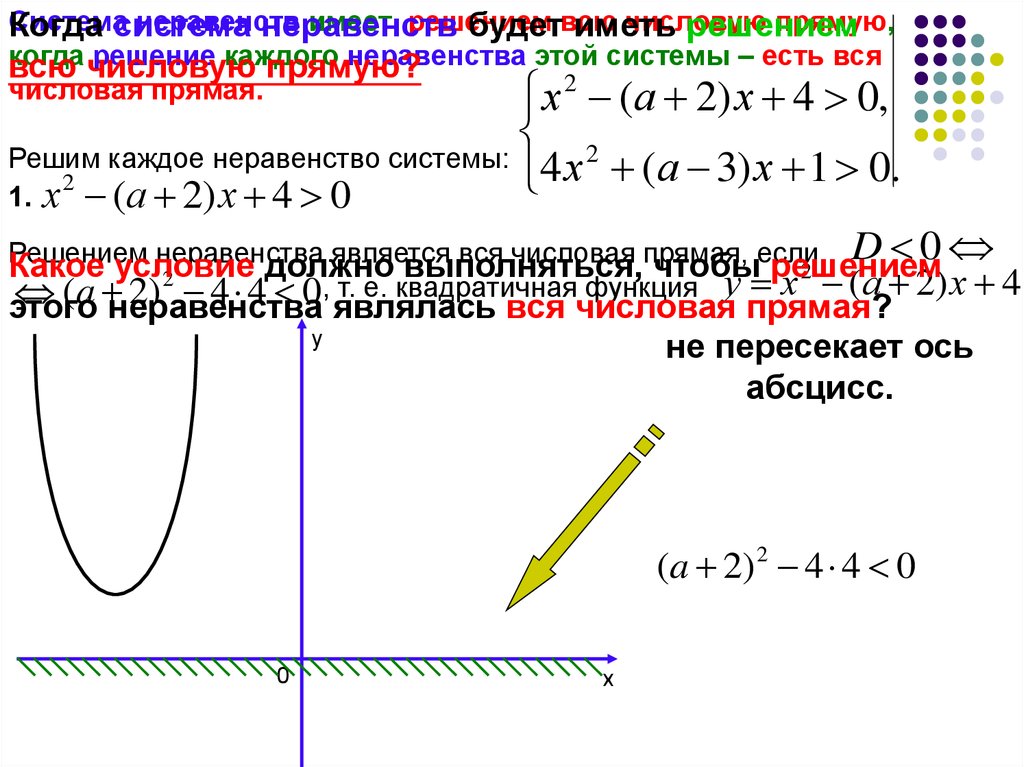
Решим каждое неравенство системы: 4 х 2 ( а 3) х 1 0.
2
1.
х (а 2) х 4 0
D
0
Решением
неравенства
является
вся числовая прямая,
если
Какое условие
должно
выполняться,
чтобы
решением
2
2
у
х
(а 2) х 4
,
т.
е.
квадратичная
функция
(a 2) 4 4 0
этого неравенства являлась вся числовая прямая?
у
не пересекает ось
абсцисс.
(a 2) 2 4 4 0
0
х

5.

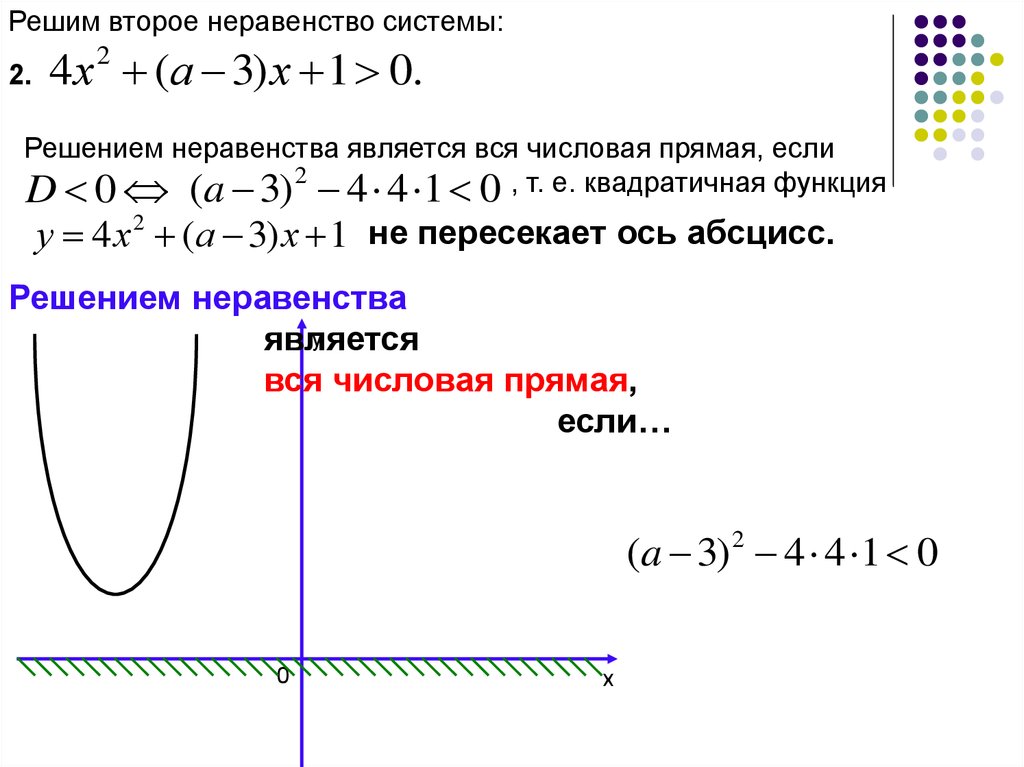
Решим второе неравенство системы:
2.
4 х (а 3) х 1 0.
2
Решением неравенства является вся числовая прямая, если
D 0 (a 3) 2 4 4 1 0 , т. е. квадратичная функция
у 4 х 2 (а 3) х 1 не пересекает ось абсцисс.
Решением неравенства
у
является
вся числовая прямая,
если…
(a 3) 2 4 4 1 0
0
х

6.

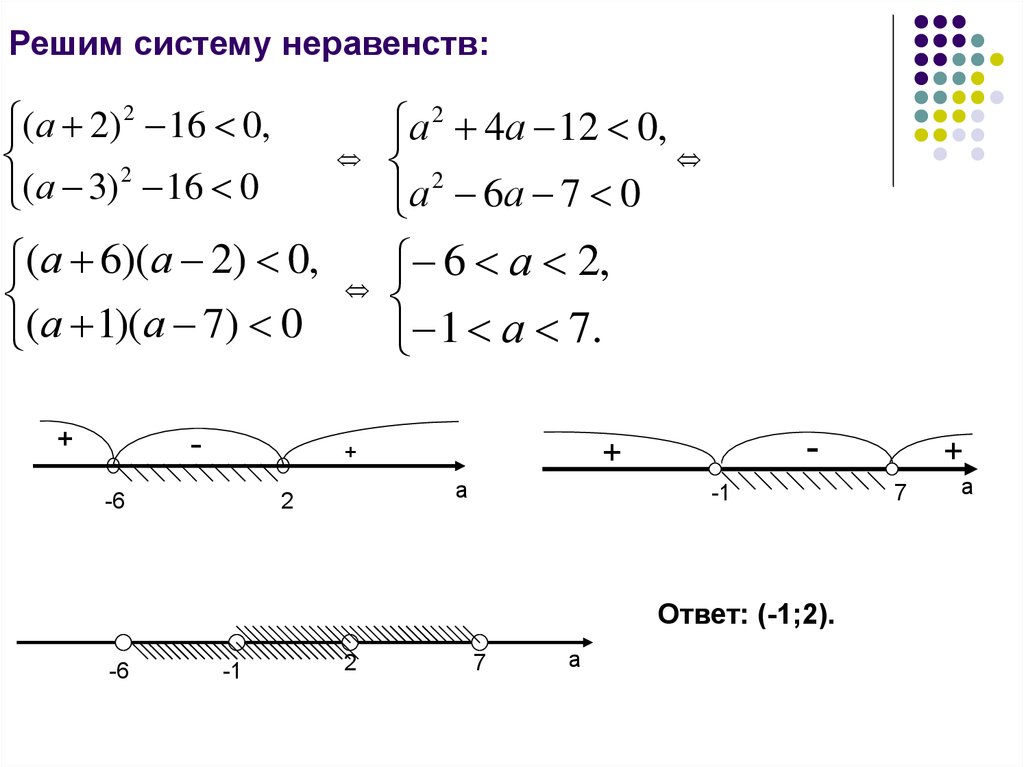
Решим систему неравенств:
(а 2) 2 16 0,
(а 3) 2 16 0
(а 6)( а 2) 0,
(а 1)( а 7) 0
+
-
а 2 4а 12 0,
2
а 6а 7 0
6 а 2,
1 а 7.
-6
а
2
-
+
+
-1
Ответ: (-1;2).
-6
-1
2
7
а
+
7
а

7.

2. При каких значениях
5
параметра р функция у (4 р) х 2 5 х (1 р)
8
определена
при всех хєR ?
Решение.
Область определения функции - множество действительных
чисел, удовлетворяющих условию… (4 р ) х 2 5 х 5 (1 р) 0
8
Какие условия должны выполняться, чтобы решением этого
неравенства (4 р ) х 2 5 х 5 (1 р ) 0 являлась вся числовая
8
прямая?
D 0,
4 р 0
р 1,
р 6,
р 4
5
25
4
(1 р)( 4 р ) 0,
8
р 4
р 1.
р 2 5 р 6 0,
р 4
Ответ:(-∞ ; -1].

8.

Домашнее задание:
3. При каких значениях параметра а
система неравенств
а) имеет единственное решение;
б) не имеет решений;
в) имеет бесконечно много
решений?
х 2 8 х 15 0,
2
х (а 4) х 4а 0.