Похожие презентации:
Інтерполяційний многочлен Ньютона. (Лекція 3)
1. Лекція №3
Інтерполяційниймногочлен Ньютона
2.
3.Нехай задана таблична функція:x
y
x
y
x x
y y
0
0
1
2
1
2
x
... y
...
n
n
Різниці І-го порядку або перші різниці визначаються
формулами:
y y y
Δ y y y
...
y
y
y
n 1
n
n 1
0
1
0
1
2
1
Різниці ІІ-го порядку або другі різниці визначаються
формулами:
2
2
2
y0 y1 y0 y1 y2 y1 ... yn 1 y n yn 1
Різниці (n+1)-го порядку або (n+1) різниці визначаються формулами:
n 1
n
n
y y y
y1 y2 y1 ... y y y
n 1
n
0
n 1
n
1
0
n
n 1
n
n
n 1
3.
Таблиця кінцевих різниць різних порядківx
x
x
x
x
x
x
...
0
1
2
3
4
5
y
y
y
y
y
y
y
...
2
∆y
0
1
2
3
4
5
3
y
y
y
y
y
...y
4
y
5
y
y
2
y 3y
4
2
y
1
y
3
2 1 y1 4 5 y
2
2 y 3 y y1
3
y
0
4
...
0
0
0
2
2
...
3
...
...
...
0
4.
Кожне число цієї таблиці (починаючи з 3-го стовпчика) єрізницею двох сусідніх чисел стовпчика зліва = від нижнього
числа віднімають верхнє,а різницю записують у наступному
стовпчику між цими числами.
Приклад 1.
xi
yi
-1
11
2
-2
4
13
8
14
5.
f ( x і ) yif xi 1 f xi yi 1
f ( xi , xi 1)
xi 1 xi
xi 1
y
x
i
i
6.
f xi 1 , xi 2 f xi , xi 1f xi , xi 1 , xi 2
xi 2 xi
f ( x0 , x1 ,..., xn)
y
x
i 2
i 2
y
x
x
i 1
i 1
i 2
y
x
x
i 1
i 1
y
x
i
i
i
f ( x1 , x2 ,..., xn) f ( x0 , x1 ,..., xn 1)
x x
n
0
7.
8.
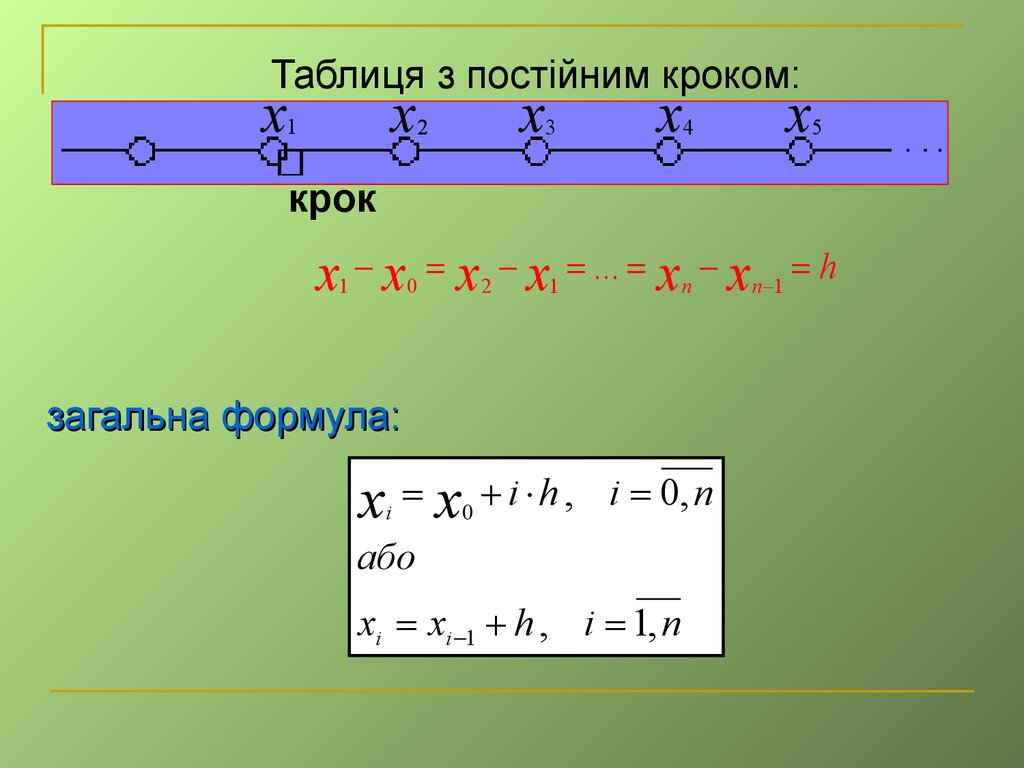
Таблиця з постійним кроком:x
x
1
x
2
3
x
x
4
5
крок
x x x x
1
0
2
1
... xn
загальна формула:
x x
i
0
i h , i 0, n
або
xi xi 1 h , i 1, n
x
n 1
h
9.
Розділені різниці для таблиці з постійним кроком:І-го порядку:
f ( xi , xi 1)
ІІ-го порядку:
y
h
f ( xi , xi 1 , xi 2)
i 1
2h
n-го порядку:
y
y
h
i
h
i
y y y
i
i
i 1 2
2h
2!h 2
2
y
f ( x , x ,..., x )
n!h
n
0
1
n
n
0
10.
5.Інтерполяційний многочлен НьютонаРозглянемо многочлен
N ( x) a a x x a x x x x ...
a x x x x ... x x
n
0
0
n
0
1
1
На рівномірній сітці з кроком h
N
n
( x і ) y , i 0, n
i
0
2
n 1
1
11.
Знайдемо коефіцієнти аіx=x0
N
N
x=x1
n
n
( x0 ) a0 y0
( x1 ) a0 a1 x1 x0 y1
y1 y0 y0
a1
x1 x0
h
12.
x=x2N ( x ) a a x x a x x x x
y
y
2h a 2h h y 2 y a 2h y
h
2
n
0
2
1
0
2
0
2
1
2
0
0
2
2
0
0
2
y2 y0 2 y0 y2 y0 2 y1 2 y0
a2
2
2
2h
2h
y2 2 y1 y0 2 y0
2
2
2h
2!h
n y0
an n
n!h
2
13.
Отримаємо многочлен Ньютона для рівномірної сіткиN n ( x) y
0
n
y
n!h
n
0
y
1!h
0
x x0
2
y
2!h
2
0
x x0 x x1 ...
(*)
x x0 x x1 ... x xn 1
«Інтерполяція вперед» використовується для знаходження
значення функції f(x) у точці x, що розташована ближче до
вузла x0
x
0
x
x
n
14.
«Інтерполяція назад» використовується для знаходження значення функції f(x) у точці x, що розташована ближче до вузла xnx xn
x0
N n ( x) y
n
y
y
(x x )
( x x )( x x
2
h
2!h
2
n 1
n 2
n
n
y
( x x )( x x )( x x )
3!h3
y
...
( x x )( x x )...( x x )
n
n!h
3
)
n 1
n 3
n
n 1
n 2
n
0
n
n 1
1
(**)
15.
Оскільки k-ий член многочлена Ньютона залежить тількивід k перших вузлів інтерполяції і від значень функції у цих
вузлах,то додавання нових вузлів призводить лише до
додавання нових членів у формулі Ньютона без зміни
попередніх
16.
У формулі (*) коефіцієнтами многочлена єскінченні різниці, що знаходяться на верхній бічній
стороні
рівнобедреного
трикутника
(одне
підкреслення у таблиці різниць);
У формулі (**) коефіцієнтами многочлена є
скінченні різниці, що знаходяться на нижній бічній
стороні
рівнобедреного
трикутника
(два
підкреслення у таблиці різниць).
17.
xy
x
x
x
x
x
x
...
0
1
2
3
4
5
y
y
y
y
y
y
...
2
y
∆y
0
1
2
3
4
5
y
y
y
y
y
0
1
...
3
y
2
2 y0
2 y1
2 y2
4
y
3
3 y0 4 y
0
4
y
3 1 y1
y
3 y
2
4
5
y
5
y
2
3
...
...
...
...
...
0
18.
Якщо коефіцієнти аі замінити на розділені різниці, тоотримаємо многочлен Ньютона для змінного кроку
N
n
( x) f x0 f ( x0 , x1 ) x x0 f ( x0 , x1 , x 2 ) x x0 x x1
.. f ( x0 , x1 ,..., x n ) x x0 x x1 ... x xn 1
Інтерполяційна формула Ньютона:
f ( x) f x0 f ( x0 , x1 ) x x0 f ( x0 , x1 , x 2 ) x x0 x x1
.. f ( x0 , x1 ,..., x n ) x x0 x x1 ... x xn 1
19.
Приклад 2.Дана таблиця значень теплоємності речовини в
завлежності від температури Cр =f(T). Визначити
значення теплоємності в точці Т=450 К, n=3; h=100
Складемо таблицю кінцевих різниць функції
20.
Скористаємось першою інтерполяцйною формулою,запишемо інтерполяційний многочлен при x=450 К.
Таким чином, теплоємність при температурі 450 К
буде: Сp(450)=71,31Дж/(моль*К).




















 Математика
Математика








