Похожие презентации:
Математический анализ. Лекция № 9
1.
Математический анализЛЕКЦИЯ № 9
ТЕОРЕМЫ
О
ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЯХ.
ИССЛЕДОВАНИЕ ФУНКЦИИ.
2.
§ 1. Теоремы о дифференцируемых функцияхОпределение 1. Говорят, что f (x) достигает в т. х=с локального максимума
( минимума), если U (c) - окрестность т.е., в которой
f (c) f ( x) [ f (c) f ( x)] x U (c)
Локальные максимумы (max) и минимумы (min) называются
экстремумами функций.
Теорема 1. (Ферма). Если f ( x) C 1[a; b] и имеет в т. x c (a; b) экстремум,
то
(1)
f (c) 0
Геометрически Т. Ферма означает, что в точке экстремума касательная к
кривой у f (x) параллельна оси Ox (рис.1).
Рисунок 1
3.
Равенство нулю производной в т. x c является условием необходимым, но не достаточнымдля существования экстремума функции.
Определение 2. Точки, в которых производная функции равна нулю или терпит разрыв,
называются критическими (стационарными).
Теорема 2. (Ролля). Пусть функция y f (x) удовлетворяет следующим условиям:
1) непрерывна на отрезке a, b ;
2) дифференцируема на интервале a, b ;
3) на концах отрезка принимает равные значения, т.е. f a f b .
Тогда внутри отрезка существует по крайней мере одна такая точка c a, b , в которой
производная функции равна нулю, т.е.
f ' c 0 .
Г е о м е т р и ч е с к и й с м ы с л т е о р е м ы Р о л я . На графике функции
найдется хотя бы одна точка, в которой касательная будет параллельна оси Ох (рис. 2).
y
y f x
а
с
b
Рисунок 2
x
4.
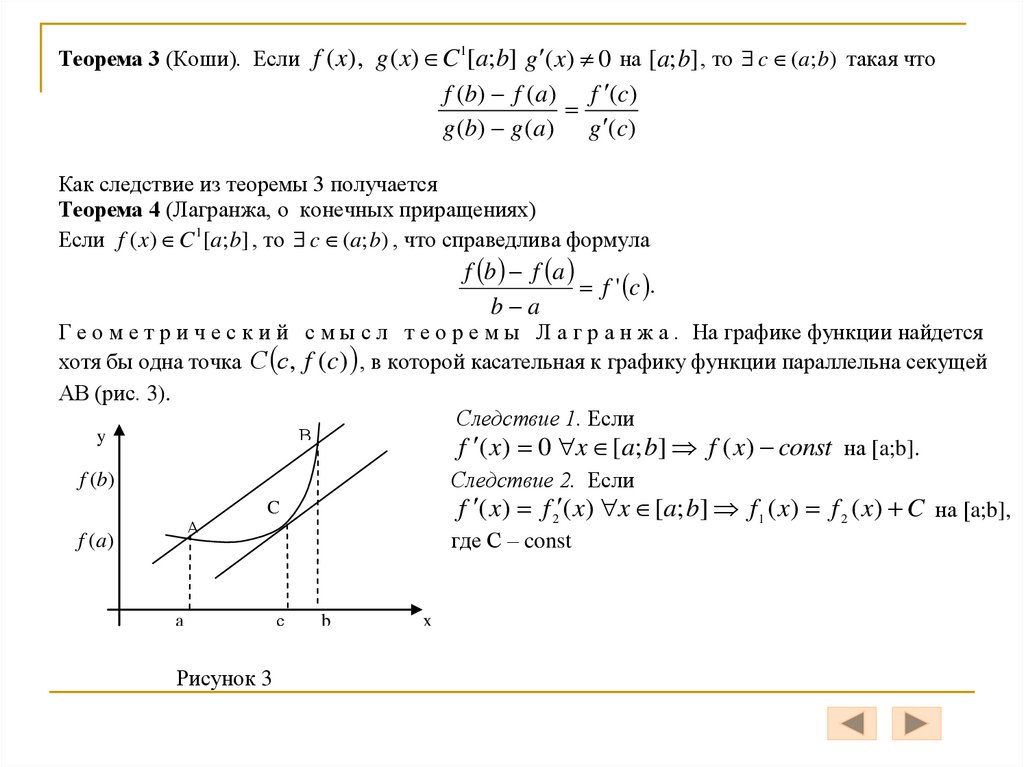
Теорема 3 (Коши). Если f ( x) , g ( x) C 1[a; b] g ( x) 0 на [a; b] , то c (a; b) такая чтоf (b) f (a) f (c)
g (b) g (a) g (c)
Как следствие из теоремы 3 получается
Теорема 4 (Лагранжа, о конечных приращениях)
Если f ( x) C 1[a; b] , то c (a; b) , что справедлива формула
f b f a
f ' c .
b a
Г е о м е т р и ч е с к и й с м ы с л т е о р е м ы Л а г р а н ж а . На графике функции найдется
хотя бы одна точка С с, f (c) , в которой касательная к графику функции параллельна секущей
АВ (рис. 3).
Следствие 1. Если
В
y
f ( x) 0 x [a; b] f ( x) const на [a;b].
f (b)
Следствие 2. Если
C
f ( x) f 2 ( x) x [a; b] f 1 ( x) f 2 ( x) C на [a;b],
А
f (a)
где С – const
a
Рисунок 3
с
b
x
5.
1.1 Правило Лопиталя. Раскрытие неопределенностей вида 0 ,Это
правило
0
дает
возможность
вычислять
пределы
0
дифференцируемых функций вида или
с использованием производных.
0
Теорема 5. Пусть y f ( x ) и y g( x ) две бесконечно малые или бесконечно
большие при x a функции, дифференцируемые в U(a ) \ {a} и пусть
f ( x )
g( x) 0 и g ( x ) 0 в U(a ) \ {a} . Тогда, если существует lim
, то
x a
g (x)
f (x)
существует lim
и они равны:
x a
g( x )
f (x)
f ( x )
= lim
.
(2)
lim
x a
x a
g ( x )
g( x )
Аналогичные утверждения справедливы для x , x ,
x , x a , x a .
Пример1.
2 ln x
1
2
ln
x
ln
x
lim ln x lim
lim x lim 2 ln x lim
2 lim x 2 lim 1 0 .
x
3x
3x
x
3x 3 3x 9 3x
2
2
x
3
x
3
x
2
x
3
x
3
x
2
x
3
6.
В формуле (2) предел левой части может существовать, а правой – нет.Пример 2.
2
2
x sin 1
x sin 1
x 0 lim
x lim x sin 1 0 .
lim
x 0
x
0
x 0
sin x
0
x
x
x2 sin 1
2x sin 1 cos 1
x
x
x lim 2x sin 1 lim cos 1 0 lim cos 1 - не
lim
lim
x 0
x 0
x 0
x 0
cos x
x x 0
x
x
sin x
существует.
Пример 3. Найти
е3 х 1
lim
x 0 sin 5 x
Числитель и знаменатель данной дроби непрерывные, дифференцируемые
функции и стремятся к нулю. Это означает, что можно применить правило
Лопиталя. Применяем его дважды:
1 cos 4 x
0
4 sin x 0
4 4 cos 4 x
lim
8.
lim
=
=
=
=
x 0
x 0
2
x2
0 x 0 2x
0
lim
7.
2.1 Раскрытие неопределенностей 0 , , 0 , 0f x A , lim g x B . Тогда
Пусть lim
x a
x a
g x
.
1
f x
1
ln x lim x 0
ln x
x ln x 0 lim
lim
Пример 4. lim
.
x 0
x 0 1
x 0
1
x 0 1
2
x
x
x
g x
f x g x lim f x 1
б) A B . Тогда lim
.
x a
x a
f
x
ln x
x ln x lim x 1
Пример 5. lim
.
x
x
x
1
ln x
lim
lim x 0 lim x 1 0 .
x x
x
x 1
f x g x 0 lim
а) A 0 , B 0 . В этом случае lim
x a
x a
8.
Пример 6.lim x sin x 0 0 y x sin x ln y sin x ln x lim ln y lim sin x ln x 0
x 0
x 0
x 0
1
ln x
sin 2 x
x2
x
x
lim
lim
lim
lim
lim
0.
x 0
x 0
x 0 x cos x
x 0 x cos x
x 0 cos x
1
cos
x
sin x
sin 2 x
Или lim ln y 0 y e 0 1.
x 0
9.
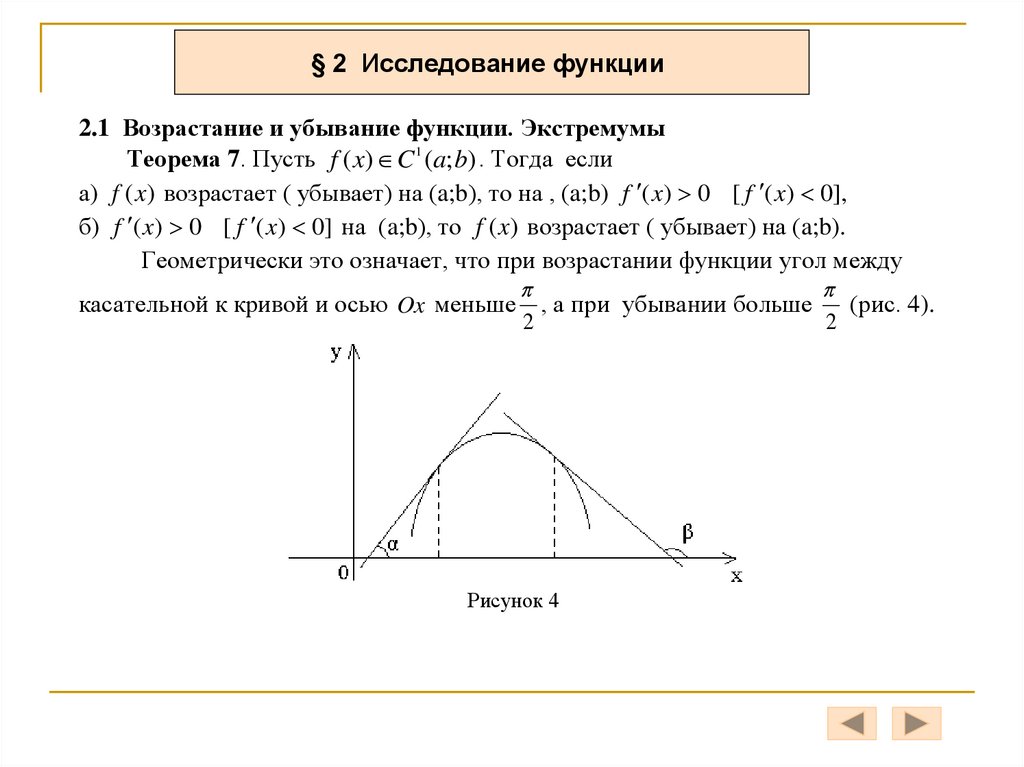
§ 2 Исследование функции2.1 Возрастание и убывание функции. Экстремумы
Теорема 7. Пусть f ( x) C 1 (a; b) . Тогда если
а) f (x) возрастает ( убывает) на (a;b), то на , (a;b) f ( x) 0 [ f ( x) 0],
б) f ( x) 0 [ f ( x) 0] на (a;b), то f (x) возрастает ( убывает) на (a;b).
Геометрически это означает, что при возрастании функции угол между
касательной к кривой и осью Ox меньше , а при убывании больше
(рис. 4).
2
Рисунок 4
2
10.
Теорема 8. (достаточные условия существования экстремума).Пусть х1 – критическая точка f (x) , а U ( x1 ) - интервал, содержащий точку х1.
Тогда, если
а) f (x) непрерывна в U ( x1 ) и дифференцируема в U ( x1 ) , кроме, может быть, т. х1, то
она имеет в т. х1 max[min], если при переходе слева направо через х1, меняет знак с + на
- [с – на +],
б) f ( x1 ) 0 и в U ( x1 ) f ( x ), то в т. х1 f (x) имеет max[min], если
f ( x1 ) 0 [ f ( x1 ) 0] .
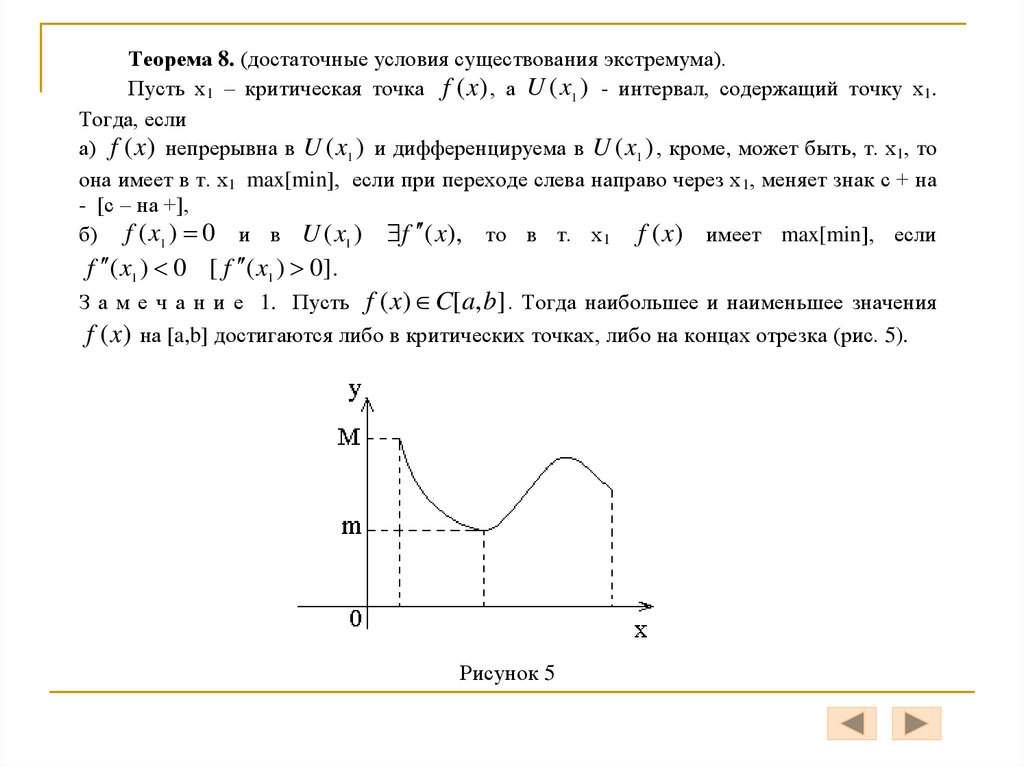
З а м е ч а н и е 1. Пусть f ( x) C[a, b] . Тогда наибольшее и наименьшее значения
f (x) на [a,b] достигаются либо в критических точках, либо на концах отрезка (рис. 5).
Рисунок 5
11.
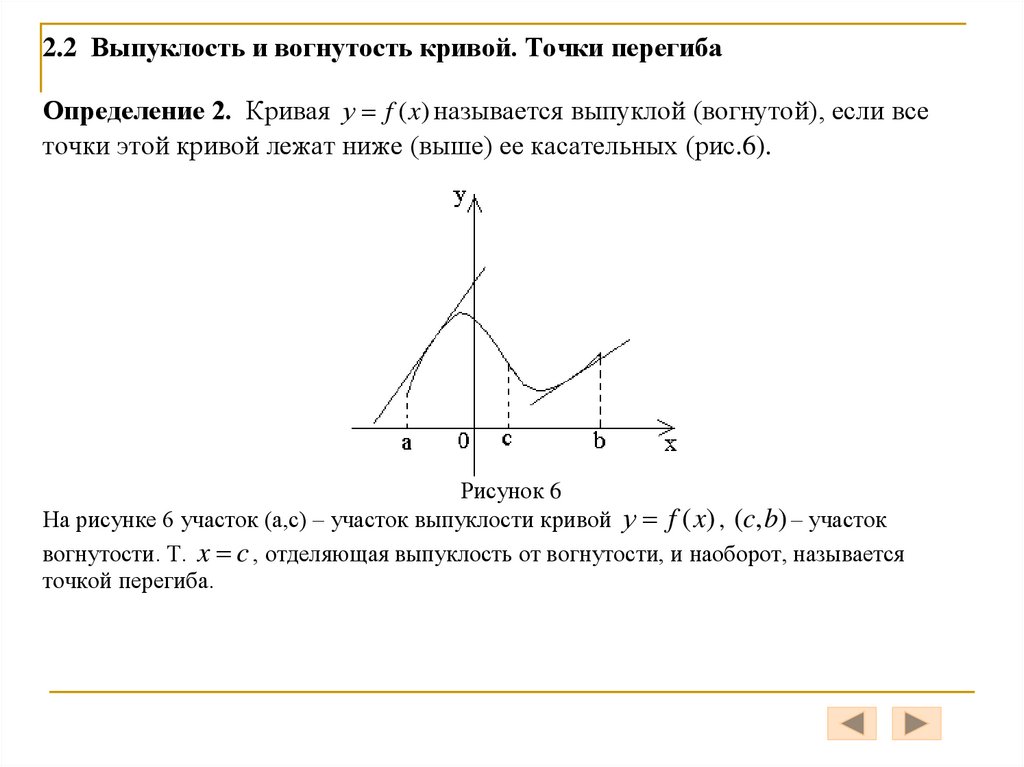
2.2 Выпуклость и вогнутость кривой. Точки перегибаОпределение 2. Кривая у f (x) называется выпуклой (вогнутой), если все
точки этой кривой лежат ниже (выше) ее касательных (рис.6).
Рисунок 6
На рисунке 6 участок (а,с) – участок выпуклости кривой у f (x) , (c, b) – участок
вогнутости. Т. x c , отделяющая выпуклость от вогнутости, и наоборот, называется
точкой перегиба.
12.
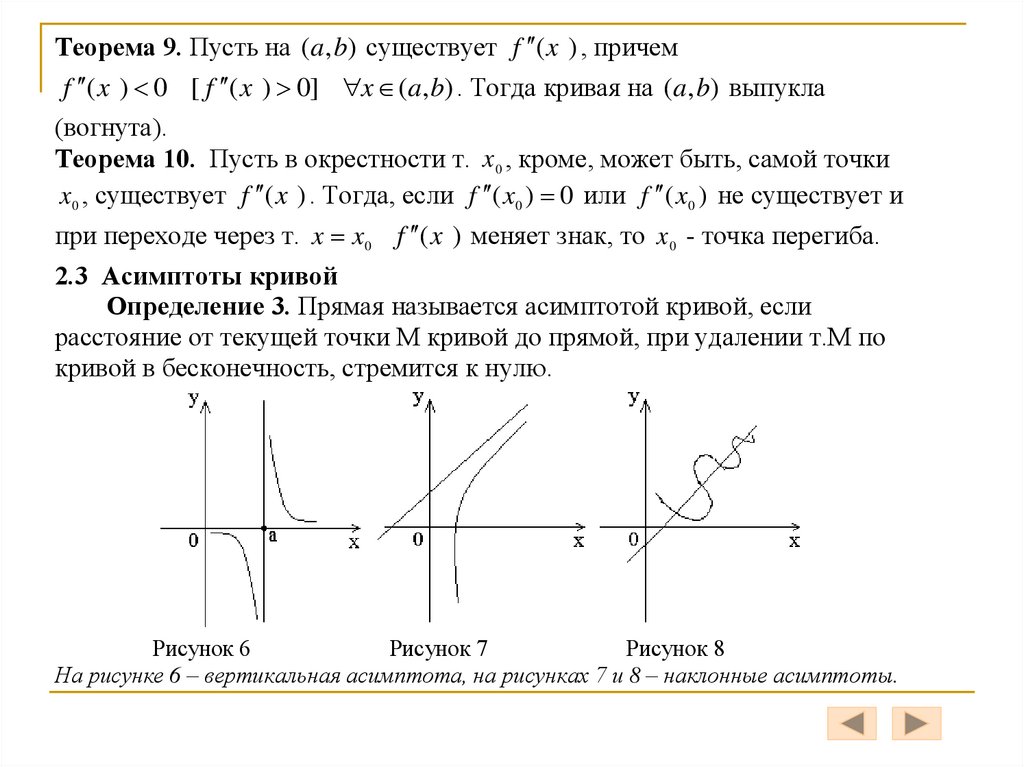
Теорема 9. Пусть на (a, b) существует f (x ) , причемf ( x ) 0 [ f ( x ) 0] x (a, b) . Тогда кривая на (a, b) выпукла
(вогнута).
Теорема 10. Пусть в окрестности т. x 0 , кроме, может быть, самой точки
x 0 , существует f (x ) . Тогда, если f ( x0 ) 0 или f ( x0 ) не существует и
при переходе через т. x x0 f (x ) меняет знак, то x 0 - точка перегиба.
2.3 Асимптоты кривой
Определение 3. Прямая называется асимптотой кривой, если
расстояние от текущей точки М кривой до прямой, при удалении т.М по
кривой в бесконечность, стремится к нулю.
Рисунок 6
Рисунок 7
Рисунок 8
На рисунке 6 – вертикальная асимптота, на рисунках 7 и 8 – наклонные асимптоты.
13.
Пусть кривая задана уравнением у f (x) . Очевидно, что вертикальнаяасимптота имеет уравнение x а , где при x а 0 или x а 0
предел f (x) стремится к .
Пусть y kx b - наклонная асимптота. Тогда
f ( x)
,
х x
k lim
b lim [ f ( x) kx]
х
Прямая может быть асимптотой при x или при x , или при
x . Поэтому пределы при x и x , в общем случае надо
брать отдельно.
2.4 Общий план исследования и построения графика функции
1. Определить область существования.
2. Определить, если они есть, точки разрыва.
3. Найти точки пересечения графика f (x) с осями координат.
4. Выяснить, является ли функция четной, нечетной, периодической
или общего вида.
5. Найти интервалы монотонности функции и экстремумы.
6. Найти интервалы выпуклости и вогнутости и точки перегиба.
7. Найти асимптоты.
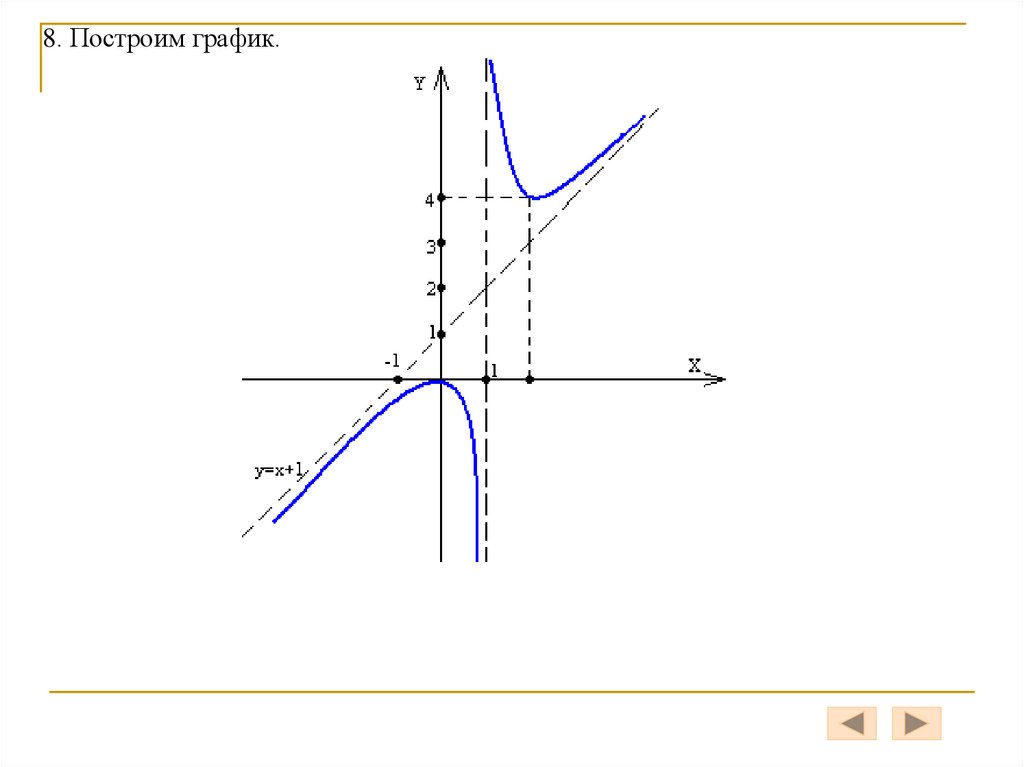
8. На основании исследования построить график функции.
14.
x2Пример. Исследовать функцию y
и построить её график.
x 1
1. Область существования вся числовая ось кроме т. x 1 .
2. Функция терпит разрыв в т. x 1 . Исследуем точку разрыва.
x2
1
1
1
f ( x) lim
lim
х 1 0
х 1 0 x 1 1 0 1
0
0
1 1
f
(
x
)
lim
х 1 0
1 0 1 0
Т. x 1 – точка разрыва 2- го рода.
3. При x 0 y 0.
В ( ;1) y 0 , в (1; ) y 0 .
4. Так как f ( x) f ( x) , f ( x) f ( x) , f ( x T ) f ( x) , то f (x) функция общего вида.
5. Определим участки возрастания, убывания, экстремумы.
x 2 2 x x( x 2) x( x 2)
y
2
2
( x 1)
( x 1)
( x 1) 2
Найдем критические точки:
15.
а) y 0 x( x 2) 0 x1 0,x2 2
б) y не существует в т. x 1 x3 1 1
Следовательно, критические точки x1 0, x2 2, x3 1 .
Найдем участки возрастания и убывания f (x) .
2
знак y совпадает со знаком x 2 x х( х 2) , т.е. необходимо решить
неравенство x 2 x 0 . Корни квадратного уравнения 0 и 2, а
2
коэффициент у х положительный. Следовательно,
2
Имеем
а) y 0 в (0;2) - в (0;2) f (x) убывает;
б) y 0 в ( ;0) и ( 2; ) - в ( ;0) и ( 2; ) f (x) возрастает;
в) при переходе через x1 0 y меняет знак с + меняет знак -, при переходе
через х2 2 - с - на + , при переходе через х3 1 - y знак не меняет.
Следовательно в т. x1 0 max y ( x) y (0) 0 , в т. x2 2
min y( x) y(2) 4 . В т. х3 1 экстремума нет.
16.
6. Найдем участки выпуклости, вогнутости, точки перегиба.2
y
( x 1) 3
Знак y совпадает со знаком (х-1). Следовательно,
а) y 0 в ( ;1) . В ( ;1) f (x) - выпукла;
б) y 0 в (1; ) . В (1; ) f (x) - вогнута;
в) В т. х=1 y не существует. При переходе через х=1 y меняет знак с –
на +. Следовательно x 1 точка перегиба.
7. Найдем асимптоты.
а) Вертикальная асимптота – x 1 .
б) наклонная асимптота y kx b
f ( x)
х2
k lim
lim
1 ,
х x
х х ( х 1)
х2
х
b lim [ f ( x) kx] lim
x lim
1
х
х х 1
х х 1
Следовательно y x 1 - асимптота при х и при х .











 Математика
Математика








