Математический анализ Раздел 2. Дифференциальное исчисление функции одной переменной

1.

Математический анализ
Раздел 2. Дифференциальное исчисление
функции одной переменной
2024 г.

2.

Дифференциальное исчисление – раздел математики,
в котором изучаются производные, дифференциалы
функций и их применение к исследованию функций.

3.

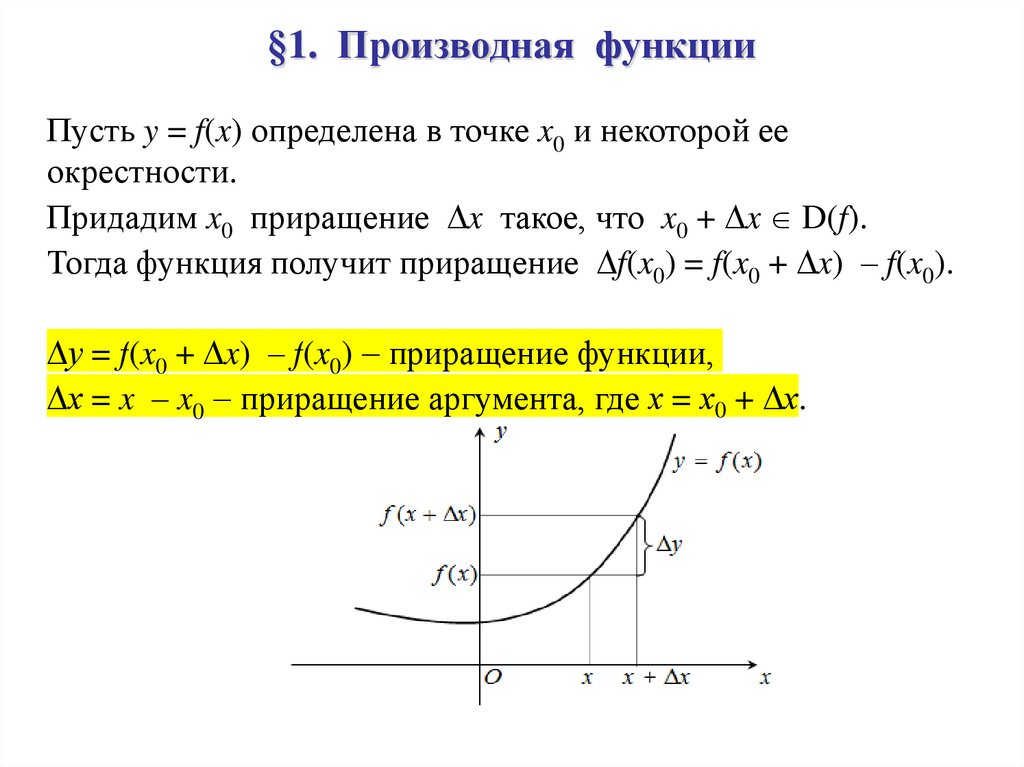
§1. Производная функции
Пусть y = f(x) определена в точке x0 и некоторой ее
окрестности.
Придадим x0 приращение x такое, что x0 + x D(f).
Тогда функция получит приращение f(x0) = f(x0 + x) – f(x0).
у = f(x0 + x) – f(x0) приращение функции,
х = x – x0 приращение аргумента, где х = х0 + х.

4.

Определение. Производной функции y = f(x) в точке x0
называется предел отношения приращения функции в этой
точке к приращению аргумента x, при x 0 (если этот
предел существует и конечен), т.е.
f ( x0 )
f ( x0 x) f ( x0 )
lim
lim
.
x 0 x
x 0
x
Обозначают: y ( x0 ) ,
dy( x0 )
,
dx
f ( x0 ) ,
df ( x0 )
.
dx

5.

Производной функции y = f(x) в точке x0 справа (слева)
называется
f ( x0 )
f ( x0 )
lim
lim
x 0 x
x 0 x
(если этот предел существует и конечен).
Обозначают:
y ( x0 ) , f ( x0 )
y ( x0 ) , f ( x0 )
– производная y = f(x) в точке x0 справа,
– производная y = f(x) в точке x0 слева.
Пропустить 2-3 страницы

6.

Теорема (необходимое и достаточное условие существования производной).
Функция y = f(x) имеет производную в точке x0 в этой
точке существуют и равны между собой производные
функции справа и слева. Причем,
f ( x0 ) f ( x0 ) f ( x0 ) .
Теорема (необходимое условие существования производной функции в точке).
Если функция y = f(x) имеет производную в точке x0, то
функция f(x) в этой точке непрерывна.
Пропустить 0,5 страницы

7.

Замечание. Непрерывность функции в точке x0 не является
достаточным условием существования в этой точке производной
функции.
Например, функция y = |x| непрерывна на всей области определения,
но не имеет производной в точке x0 = 0.
Пропустить 0,5 страницы

8.

Производную функции y = f(x) обозначают так:
y ,
dy
,
dx
f ( x) ,
df
.
dx
Определение. Функцию, которая имеет производную в точке х0,
называют дифференцируемой в точке х0.
Определение. Операцию нахождения для функции y = f(x) ее
производной функции называют дифференцированием
функции f(x).

9. Физический и геометрический смысл производной

1. Физический смысл производной.
Если функция y = f(x) и ее аргумент x являются физическими
величинами, то производная f (x) – скорость изменения
величины y относительно величины x .
Примеры.
1. Пусть S = S(t) – расстояние, проходимое точкой за время t.
Тогда производная S (t0) – скорость в момент времени t0.
2. Пусть q = q(t) – количество электричества, протекающее
через поперечное сечение проводника за время t.
Тогда q (t0) – скорость изменения количества электричества
в момент времени t0, т.е. сила тока в момент времени t0.
3. Пусть m = m(x) – масса отрезка [a ; x].
Тогда m (x0) – скорость изменения массы в точке x0, т.е.
линейная плотность в точке x0.

10.

2. Геометрический смысл производной
Пусть ℓ – некоторая кривая, M0 – точка на кривой ℓ.
Любая прямая, пересекающая ℓ не менее чем в двух точках,
называется секущей.
Определение. Касательной к кривой ℓ в точке M0
называется предельное положение секущей M0M1, если
точка M1 стремится к M0, двигаясь по кривой.
M1
M0
Если касательная к кривой в точке
единственная.
M0 существует, то она

11.

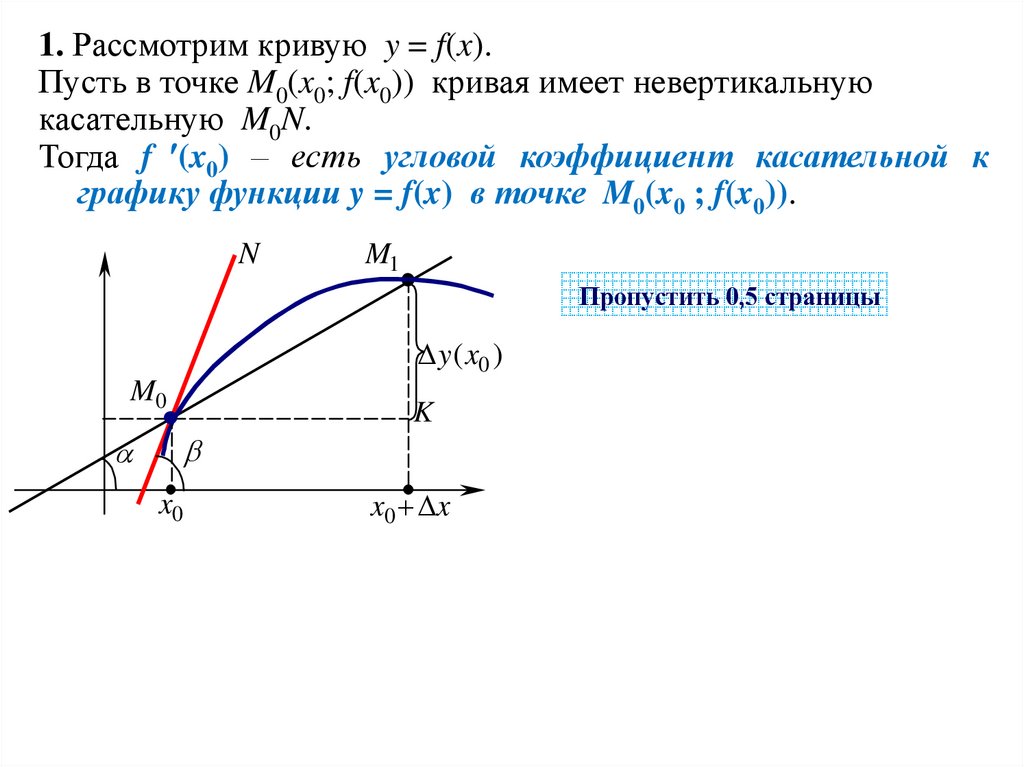
1. Рассмотрим кривую y = f(x).
Пусть в точке M0(x0; f(x0)) кривая имеет невертикальную
касательную M0N.
Тогда f (x0) – есть угловой коэффициент касательной к
графику функции y = f(x) в точке M0(x0 ; f(x0)).
N
M1
Пропустить 0,5 страницы
y ( x0 )
M0
K
x0
x0 x

12.

Уравнение касательной к кривой y = f(x) в точке M0(x0 ; f(x0))
можно записать в виде
y f ( x0 ) f ( x0 ) ( x x0 ).
Определение. Прямая, проходящая через точку M0
перпендикулярно касательной, проведенной к кривой в точке
M0, называется нормалью к кривой в точке M0.
Так как для перпендикулярных прямых справедливо равенство
k1 k2 = –1, где k1 = f (x0), то уравнение нормали к кривой
y = f(x) в точке M0(x0 ; f(x0)) будет иметь вид
1
y f ( x0 )
( x x0 ) , если f (x0) 0.
f ( x0 )
Замечание. Если же f (x0) = 0, то касательная к кривой y = f(x)
в точке M0(x0 ; f(x0)) будет иметь вид:
y = f(x0),
а нормаль: x = x0.

13.

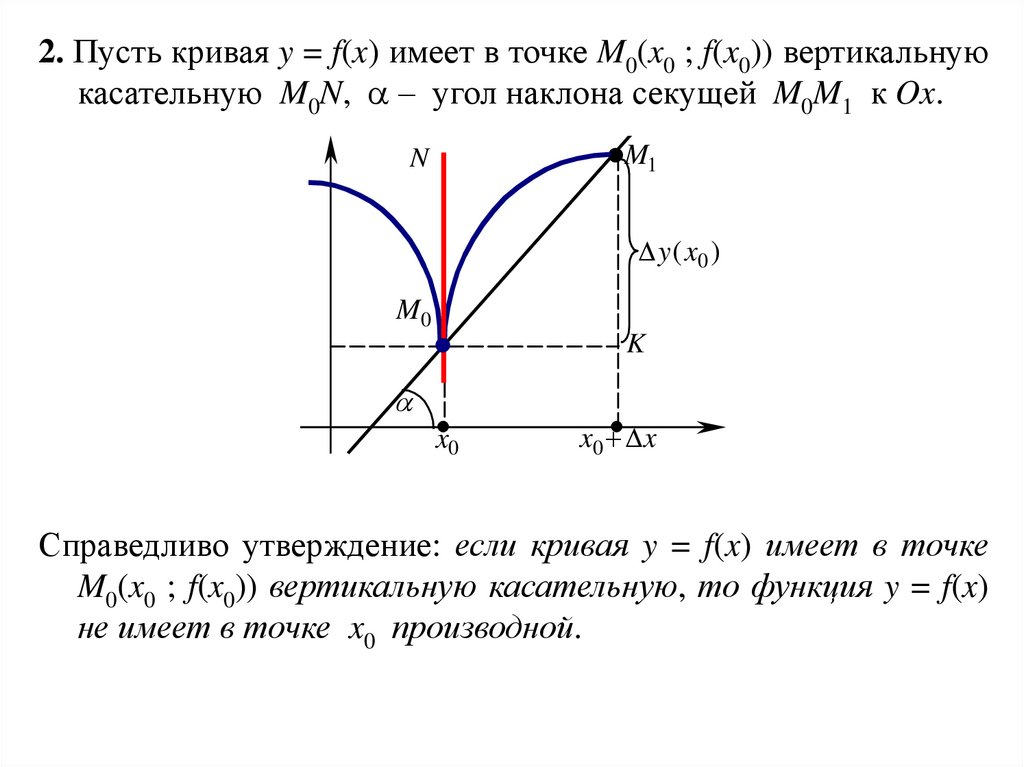
2. Пусть кривая y = f(x) имеет в точке M0(x0 ; f(x0)) вертикальную
касательную M0N, – угол наклона секущей M0M1 к Ox.
M1
N
y ( x0 )
M0
K
x0
x0 x
Справедливо утверждение: если кривая y = f(x) имеет в точке
M0(x0 ; f(x0)) вертикальную касательную, то функция y = f(x)
не имеет в точке x0 производной.

14. Правила дифференцирования

1. Производная суммы (разности) равна сумме (разности)
производных, т.е.
(u v) u v .
Доказательство Пропустить 0,3 страницы
2. Производная произведения находится по правилу:
(u v) u v u v
Доказательство Пропустить 0,5 страницы
3. Константу можно вынести за знак производной:
, где С – константа.
Доказательство Пропустить 0,5 страницы
4. Производная дроби находится по правилу:
u u v u v
v
v2
v( x) 0 .

15.

6. Правило дифференцирования сложной функции.
Если функция (t) имеет производную в точке t, а функция
f(u) имеет производную в точке u = (t), то сложная
функция y = f( (t)) имеет производную в точке t, причем
y f (u ) u .
7. Теорема (о производной обратной функции).
Пусть функция y = f(x) имеет производную в точке x0,
причем f (x0) 0. Если существует обратная функция
x = (y), то она имеет производную в точке y0 = f(x0) и
1
( y0 )
f ( x0 ) .
Доказательство
Пропустить 0,3 страницы

16.

Пример. Найти производную функции y = arcsinx.
Пропустить 1 страницу

17.

Таблица производных основных элементарных функций

18.

Производная показательно-степенной функции
Пусть u = u(x) и v = v(x).
Функция у = u(x)v(x) называется показательно-степенной.
Прологарифмируем обе части равенства по основанию е
и выразим у:
Найдем производную функции у и преобразуем ее:
Таким образом,

19.

Аналитический способ задания функции в ДСК
1) у = f (x) уравнение функции,
заданной явно
2) F (x, y) = 0 уравнение функции,
заданной неявно
3) x = x(t),
y = y(t)
параметрические
уравнения кривой

20.

Неявно заданная функция у = у(х), определяемая
одним уравнением

21.

22.

23.

Дифференцирование функции, заданной неявно
Пусть дано уравнение F(x, y) = 0, не разрешенное
относительно у, где = f(x). В этом случае говорят, что функция
задана неявно.
Для нахождения производной неявно заданной функции,
надо продифференцировать обе части равенства F(x, y) = 0 по х,
рассматривая функцию у как функцию от х.
Затем из полученного равенства надо выразить у .

24.

25.

Функция, заданная параметрически
Говорят, что функция у(х) задана параметрически, если
переменные х и у можно выразить через другую
переменную t:
Переменная t называется параметром.

26. Построение графиков функций, заданных параметрически

Пример.
Построить кривую, заданную уравнением x a cos t ,
y b sin t
Подготовим таблицу значений x и y
t
x
y
0
a
0
p/6
√3/2 a
½b
p/4
√2/2 a
√2/2 b
p/3
½a
√3/2 b
p/2
0
b
в I четверти
y
O
x

27.

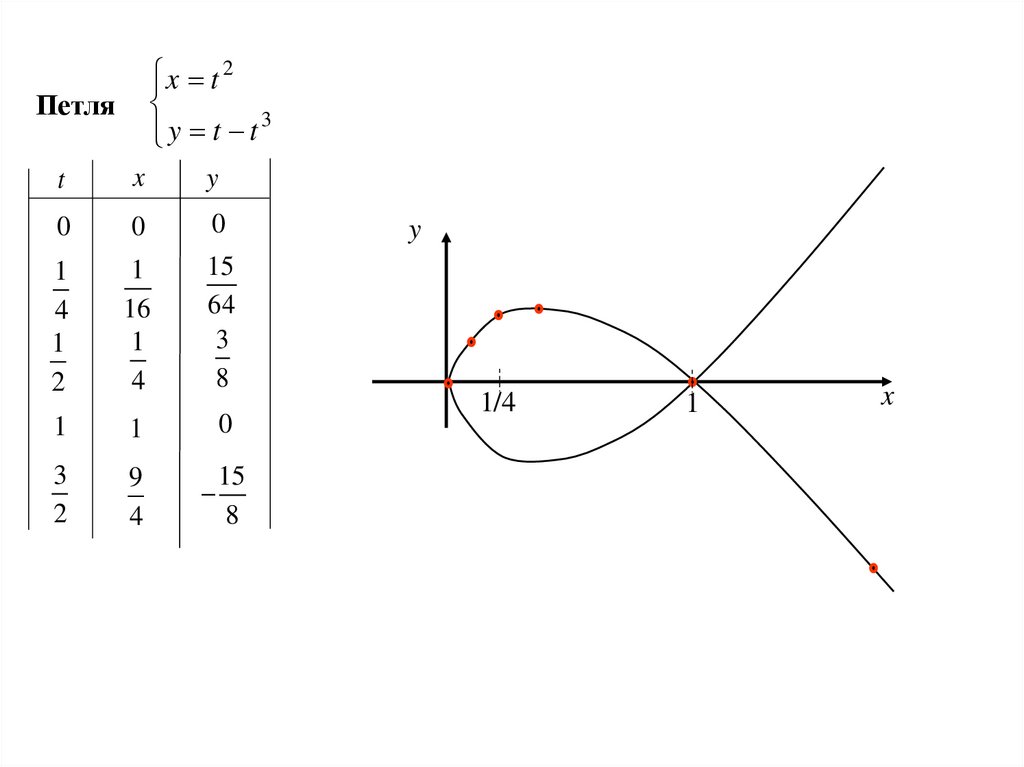
x t 2
y t t 3
Петля
t
x
y
0
0
0
1
4
1
2
1
16
1
4
15
64
3
8
1
1
0
3
2
9
4
15
8
y
1/4
1
x

28.

Дифференцирование функции, заданной
параметрически
Пусть функция у(х) задана параметрически уравнениями:
Выразим из первого равенства х = х(t) переменную t = t(x) и
подставим в у(х). Получим сложную функцию от t:
у (t(х)).
Тогда

29.

Обозначим
Тогда
Теорема. Пусть функции х = х(t) и у = у(t) имеют производные
в точке t (a; b): у t и х t 0. Кроме того, функция х = х(t)
имеет обратную функцию t = t(x) в окрестности точке t.
Тогда для функции, заданной параметрически, имеет место
формула:

30. §2. Дифференциал функции

1. Определение и геометрический смысл
Определение. Функция y = f(x) называется дифференцируемой в точке x0, если ее приращение в этой точке может
быть записано как сумма линейной относительно x части
и бесконечно малой более высокого порядка чем x, т.е.
f(x0) = A x + ( x),
(1)
где A – число, ( x) – б.м. более высокого порядка чем x.
Слагаемое A x в выражении (1) называют дифференциалом
функции y = f(x) в точке x0.
Дифференциал функции y = f(x) обозначают: dy, df(x).

31.

Теорема (о связи дифференцируемости с существованием
производной).
Функция y = f(x) дифференцируема в точке x0 она имеет
в точке x0 производную. При этом справедливо равенство:
dy(x0) = f (x0) x.
Доказательство

32.

Операцию
нахождения
производной
дифференцированием функции.
называют
Определение. Функция y = f(x) называется дифференцируемой на интервале (a; b), если она имеет производную
в каждой точке этого интервала.
Функция y = f(x) называется дифференцируемой на отрезке [a; b], если она дифференцируема на интервале (a; b) и
имеет соответствующие односторонние производные
в точках a и b.

33.

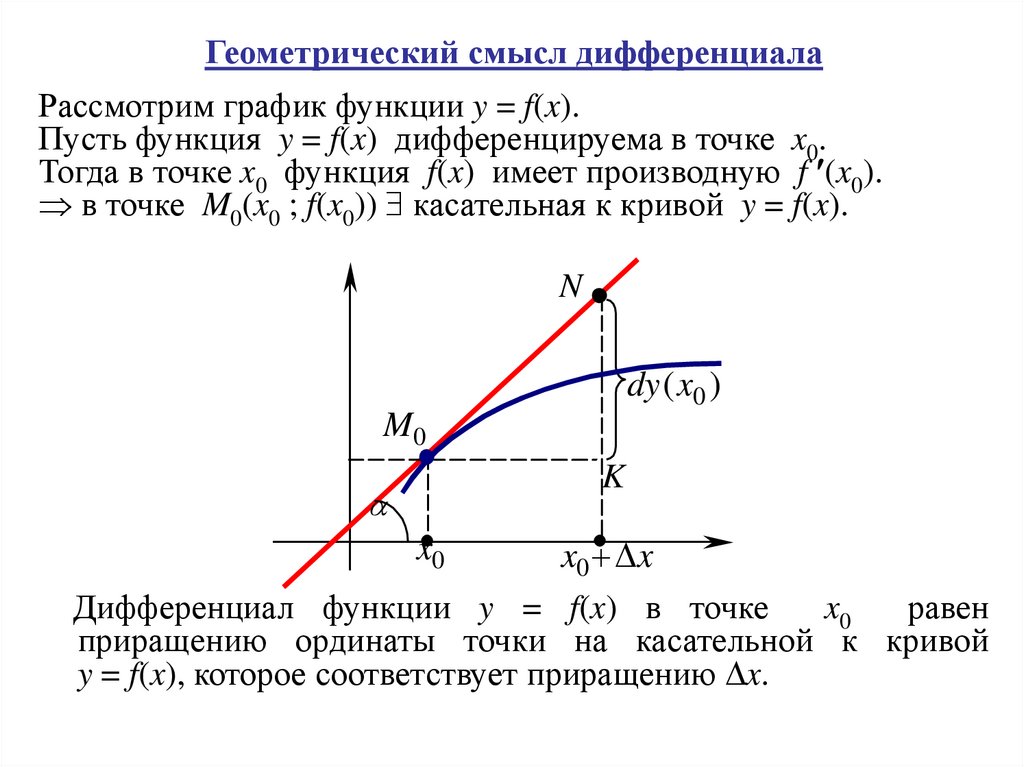
Геометрический смысл дифференциала
Рассмотрим график функции y = f(x).
Пусть функция y = f(x) дифференцируема в точке x0.
Тогда в точке x0 функция f(x) имеет производную f (x0).
в точке M0(x0 ; f(x0)) касательная к кривой y = f(x).
N
dy ( x0 )
M0
K
x0 x
Дифференциал функции y = f(x) в точке
x0
равен
приращению ординаты точки на касательной к кривой
y = f(x), которое соответствует приращению x.
x0

34.

Замечания.
1. Для дифференциала функции y = x справедливо
dy = dx = x.
Учитывая, что dx = x формулу dy(x0) = f (x0) x можно
записать в виде
dy = f (x) dx.
2. Из формулы dy = f (x) dx. получим, что производная
y = f (x) является отношением 2-х дифференциалов:
dy
y f ( x) .
dx

35. 2. Свойства дифференциалов

1. d(C) = 0, где C – константа.
2. d(u v) = du dv.
3. d(u v) = du v + u dv.
4. d(C u) = C du где C – константа.
u du v u dv
, v( x) 0 .
5. d
2
v
v
6. Свойство инвариантности дифференциала.
Если y = f(u), где u = (х), то dy = yx dx = yu du.

36.

Формула приближенного вычисления
По определению f(x0) = dy(x0) + ( x), где ( x) б.м.
при х 0.
Следовательно,
Тогда
или
(*)
Формула (*) называется формулой приближенного
вычисления значения функции в точке (х0 + х).

37. §3. Производные и дифференциалы высших порядков

1. Производные высших порядков
Пусть y = f(x) дифференцируема на множестве X1 D(f).
Функцию f (x)
функции f(x).
называют производной первого порядка
Если f (x) дифференцируема на некотором множестве X2 X1,
то (f (x)) называют производной второго порядка функции
f(x) и обозначают
y ,
d2y
,
2
dx
f ( x),
d2 f
.
2
dx

38.

И так далее.
Тогда n-й производной функции y = f(x) называют ее
производную от производной порядка (n – 1).
Обозначают:
d3y
d3 f
– третья производная y = f(x);
y ,
, f ( x) ,
3
3
dx
dx
y (n) ,
dny
,
n
dx
f ( n ) ( x) ,
dn f
dx n
– n-я производная y = f(x).
Производные порядка n > 1 называют производными высших
порядков.

39.

Производные высших порядков неявно заданных функций
Пусть функция F(x, y) = 0, где у = у(х), задана неявно.
Продифференцируем обе части равенства по х и разрешим
уравнение относительно у .
Получим у = (х, у).
Продифференцируем обе части равенства у = (х, у) по х,
учитывая, у = у(х).
Затем в полученное равенство подставим у = (х, у) и
найдем у .
И так далее.

40.

Производные высших порядков от функций, заданных
параметрически
Пусть функция задана параметрически
Производную первого порядка находят по формуле:
Производную порядка n от параметрически заданной
функции находят по формуле:

41.

Физический смысл первой и второй производной
Если S = S(t) – расстояние, проходимое точкой за время t,
то S (t0) – скорость в момент времени t0,
S (t0) – ускорение в момент времени t0 (скорость изменения
скорости).

42.

Свойства производной порядка n
1. (C u)(n) = C u(n), где C – константа.
2. (u v)(n) = u(n) v(n).
3. n-я производная произведения двух функций находится по
формуле:
где u(0) = u, v(0) = v,
число сочетаний из n по k.

43. 2. Дифференциалы высших порядков

Пусть y = f(x) дифференцируема на множестве X1 D(f).
Рассмотрим дифференциал dy = f (x) dx как функцию
переменной x, зафиксировав значение dx.
Дифференциал функции dy(x) (если он существует) называют
дифференциалом второго порядка функции y = f(x).
Обозначают: d 2y, d 2f(x).
Продолжая процесс, определим дифференциал n-го порядка
функции y = f(x)
как дифференциал от дифференциала порядка (n – 1).
Обозначают: d ny, d nf(x).

44.

Дифференциалы порядка n > 1 называют дифференциалами
высших порядков.
Если функция имеет дифференциал порядка n, то ее называют
n раз дифференцируемой.
Теорема (о связи дифференциала n-го порядка и n-й
производной).
Функция y = f(x) n раз дифференцируема в точке x0 она
имеет в точке x0 производную порядка n. При этом для
d ny(x0) справедливо равенство
d ny(x0) = f (n)(x0) (dx)n.
Обычно (dx)n записывают в виде dxn.

45. §4. Основные теоремы дифференциального исчисления

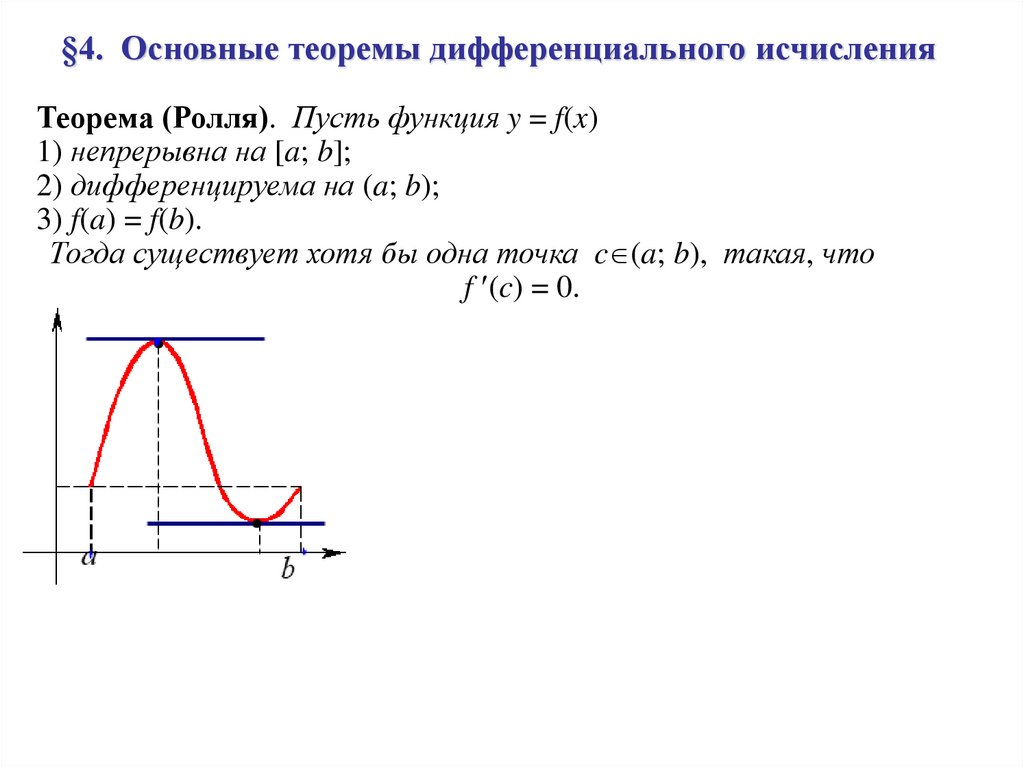
Теорема (Ролля). Пусть функция y = f(x)
1) непрерывна на [a; b];
2) дифференцируема на (a; b);
3) f(a) = f(b).
Тогда существует хотя бы одна точка c (a; b), такая, что
f (c) = 0.

46. Геометрический смысл теоремы Ролля

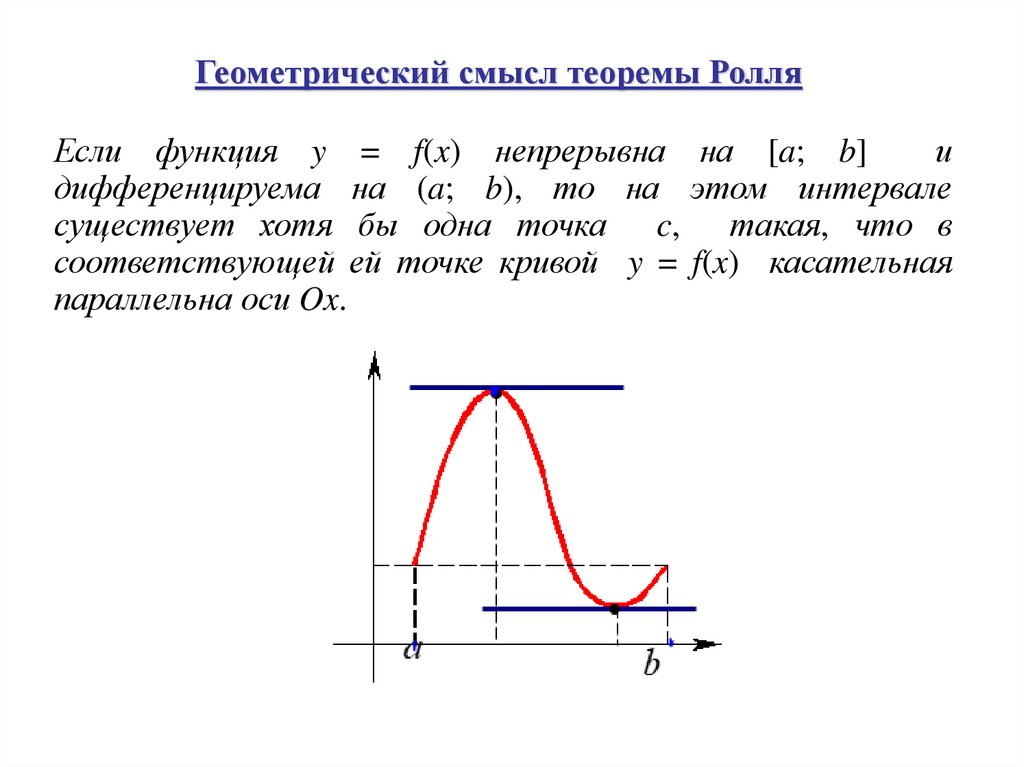
Если функция y = f(x) непрерывна на [a; b]
и
дифференцируема на (a; b), то на этом интервале
существует хотя бы одна точка c, такая, что в
соответствующей ей точке кривой y = f(x) касательная
параллельна оси Ox.

47.

Теорема (Лагранжа).
Пусть функция y = f(x) непрерывна на [a; b] и дифференцируема
на (a; b).
Тогда существует хотя бы одна точка c (a; b), такая, что

48.

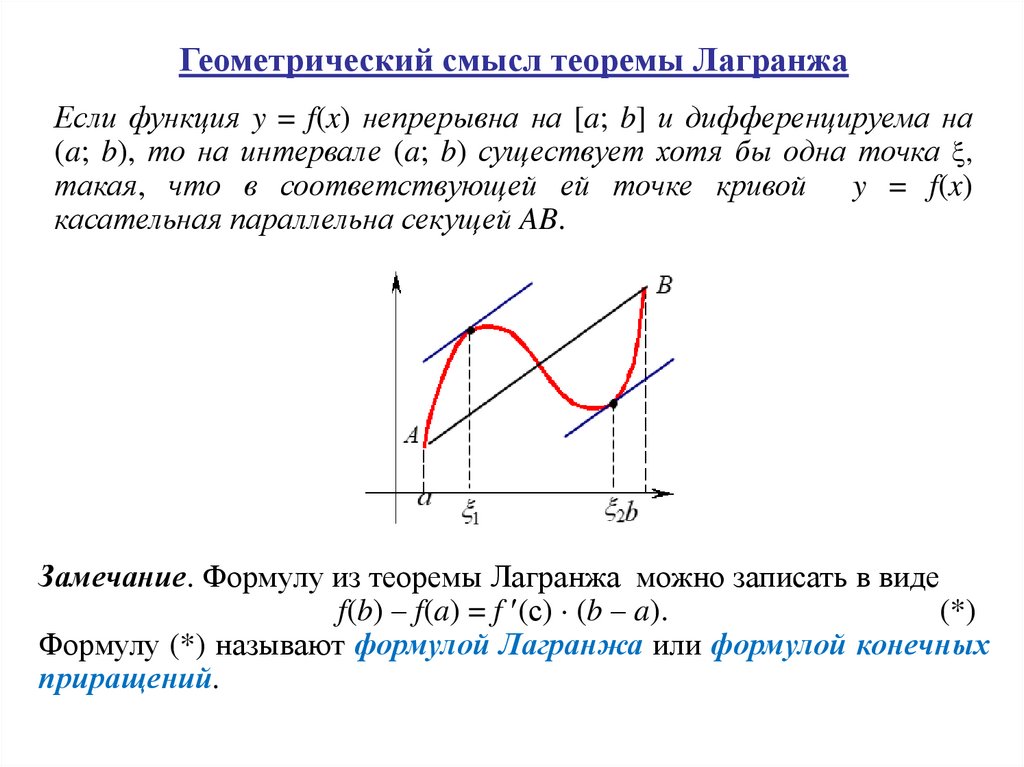
Геометрический смысл теоремы Лагранжа
Если функция y = f(x) непрерывна на [a; b] и дифференцируема на
(a; b), то на интервале (a; b) существует хотя бы одна точка ,
такая, что в соответствующей ей точке кривой y = f(x)
касательная параллельна секущей AB.
Замечание. Формулу из теоремы Лагранжа можно записать в виде
f(b) – f(a) = f (с) (b – a).
(*)
Формулу (*) называют формулой Лагранжа или формулой конечных
приращений.

49.

Теорема (Коши).
Пусть функции f(x) и (x) непрерывны на [a; b] и
дифференцируемы на (a; b), причем (x) 0 x (a; b).
Тогда существует хотя бы одна точка с (a; b), такая, что

50. §5. Использование производной при вычислении пределов

Теорема (Правило Лопиталя, 0/0).
Пусть функции f(x) и g(x) дифференцируемы в окрестности
точки x0, причем g (x) 0 в окрестности точки x0.
Если
1)
2)
Тогда конечный
причем

51.

Теорема (Правило Лопиталя, / ).
Пусть функции f(x) и g(x) дифференцируемы в окрестности
точки x0, причем g (x) 0 в окрестности точки x0.
Если
1)
2)
Тогда конечный
причем

52.

Замечания.
1. Если f (x) и (x) тоже являются б.м. (б.б.) при x x0
(x ), то правило Лопиталя можно применить повторно.
f ( x)
2. Если lim
не существует, то правило Лопиталя нельзя
x x0 ( x)
применить.

53.

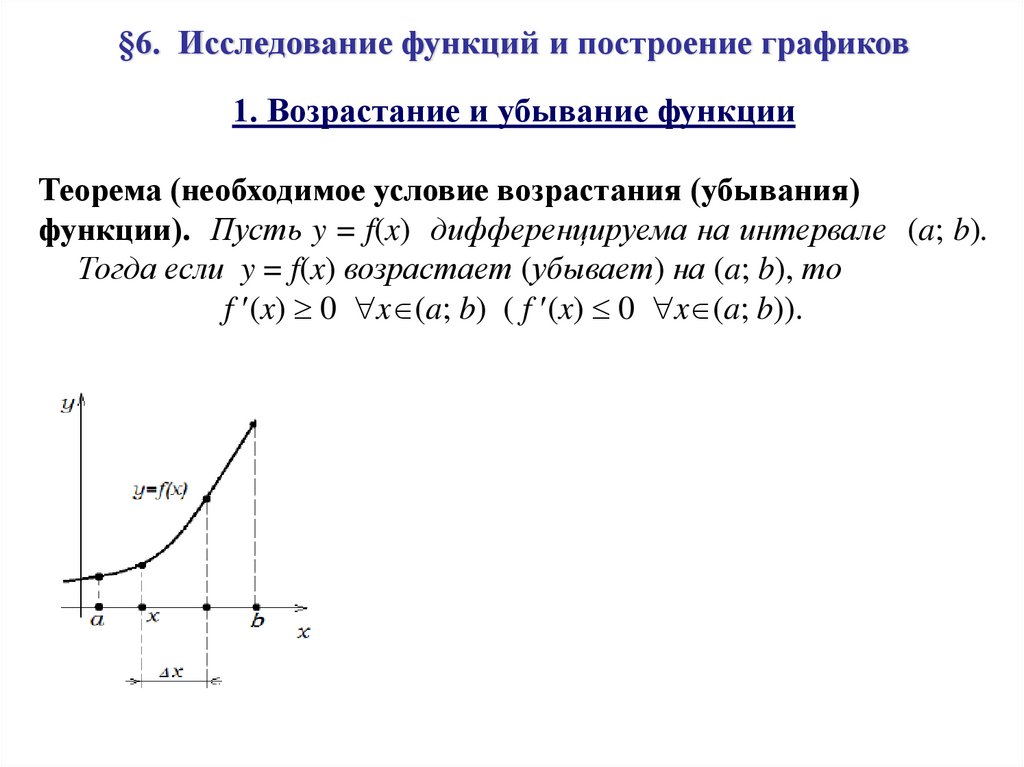
§6. Исследование функций и построение графиков
1. Возрастание и убывание функции
Теорема (необходимое условие возрастания (убывания)
функции). Пусть y = f(x) дифференцируема на интервале (a; b).
Тогда если y = f(x) возрастает (убывает) на (a; b), то
f (x) 0 x (a; b) ( f (x) 0 x (a; b)).

54.

Теорема (достаточное условие строгой монотонности).
Если f (x) > 0 x (a; b) ( f (x) < 0 x (a; b)),
то функция y = f(x) на (a; b) возрастает (убывает).

55. 2. Экстремумы функции

Пусть функция у = f(x) определена в некоторой окрестности
точки x0 D(f ).
Определение. Точка x0 называется точкой максимума
функции f(x), если существует такая -окрестность
U(x0, ) точки x0, что
f(x) < f(x0) x U*(x0, ).
Определение. Точка
x0
называется точкой минимума
функции f(x), если существует такая -окрестность
U(x0, ) точки x0, что
f(x) > f(x0) x U*(x0, ).
Точки минимума и максимума функции называются ее точками
экстремума.

56.

Основные определения
Значение функции точке максимума называется максимумом
функции.
Значение функции точке минимума называется минимумом
функции.
Точки минимума и максимума функции называются ее
точками экстремума.
Минимумы и максимумы функции называются ее экстремумами.
Точки функции f(x), в которых f (x) = 0 называются
стационарными точками.
Точки функции f(x), в которых f (x) = 0 или не существует,
называются критическими точками I рода.

57.

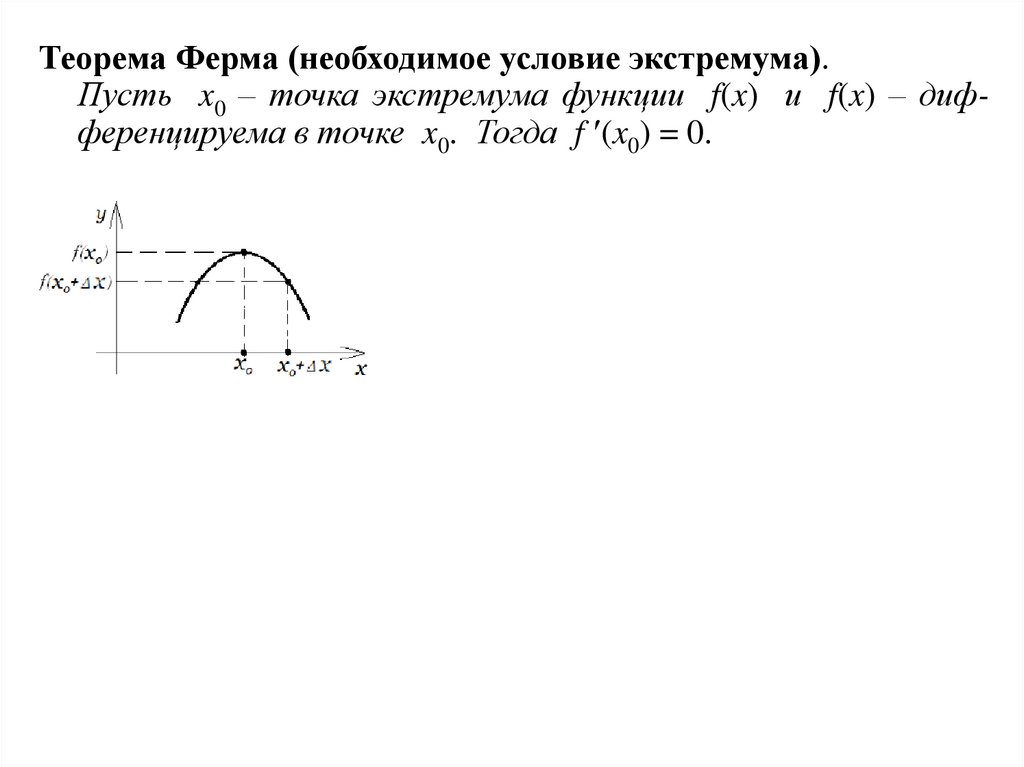
Теорема Ферма (необходимое условие экстремума).
Пусть x0 – точка экстремума функции f(x) и f(x) – дифференцируема в точке x0. Тогда f (x0) = 0.

58.

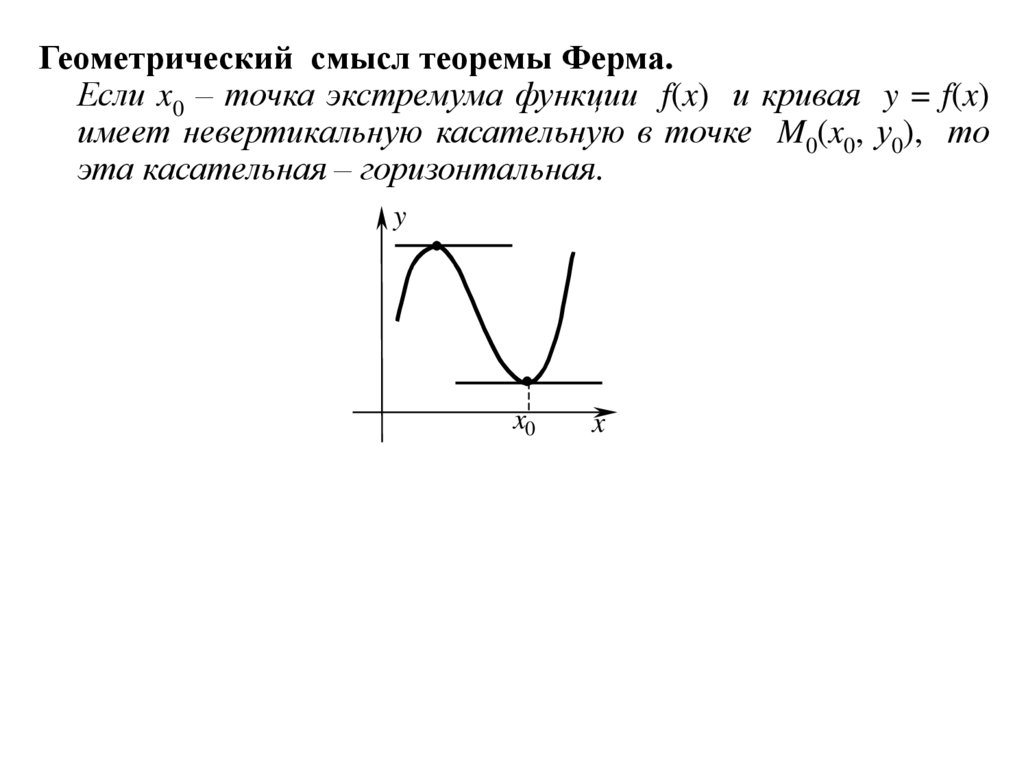
Геометрический смысл теоремы Ферма.
Если x0 – точка экстремума функции f(x) и кривая y = f(x)
имеет невертикальную касательную в точке M0(x0, у0), то
эта касательная – горизонтальная.
y
x0
x

59.

Теорема (первое достаточное условие экстремума).
Пусть f(x) непрерывна и дифференцируема в U(x0, ) или U*(x0, ) и
x0 D(f ) критическая точка.
Тогда:
а) если производная меняет знак с «+» на « », то x0 – точка максимума;
б) если производная меняет знак с « » на «+», то x0 – точка минимума.

60. 3. Выпуклость и вогнутость кривой. Точки перегиба

Пусть ℓ – кривая, M0 – точка кривой.
Определение. Кривую ℓ называют выпуклой в точке M0,
если в некоторой окрестности этой точки кривая лежит
ниже касательной, проведенной к ℓ в точке M0.
Определение. Кривую ℓ называют вогнутой в точке M0,
если в некоторой окрестности этой точки кривая лежит
выше касательной, проведенной к ℓ в точке M0.
M0
M0

61.

Точки кривой, которые разделяют ее выпуклые и вогнутые
участки, называются точками перегиба кривой.
Замечание.
В точке перегиба касательная к кривой (если она существует)
пересекает кривую (кривая переходит с одной стороны
касательной на другую).

62.

Определение. Кривая y = f(x) называется выпуклой (вогнутой)
на интервале (a; b), если x (a; b) кривая выпукла
(вогнута) в соответствующей точке M(x; f(x)).
Замечания.
1. Если M0(x0 ; f(x0)) – точка перегиба кривой y = f(x), то x0 –
внутренняя точка области определения функции f(x).
2. Точками перегиба кривой y = f(x) часто называют точки,
которые разделяют интервалы выпуклости и вогнутости этой
кривой (т.е. абсциссы точек перегиба кривой y = f(x)).
Определение. Точки, в которых y = 0 или имеет разрыв,
называют критическими точками II рода функции y = f(x).

63.

Теорема (необходимое и достаточное условия выпуклости
(вогнутости) графика функции).
Пусть функция y = f(x) дважды дифференцируема на
интервале (a; b). Тогда:
1) если кривая y = f(x) выпукла (вогнута) на интервале (a;b),
то
f (x) 0 (f (x) 0) x (a; b);
(необходимое условие выпуклости (вогнутости) графика)
2) если
f (x) < 0 (f (x) > 0) x (a; b),
то кривая y = f(x) выпукла (вогнута) на интервале (a; b).
(достаточное условие выпуклости (вогнутости) графика)
Без доказательства

64.

Теорема (достаточное условие перегиба кривой y = f(x)).
Пусть x0 D(f) и функция f(x) дважды дифференцируема в
U*(x0, ).
Если при переходе через точку x0 функция f (x) меняет знак,
то точка M0(x0; f(x0)) является точкой перегиба кривой
y = f(x).

65. 4. Асимптоты кривой

Определение. Прямая ℓ называется асимптотой кривой, если
при неограниченном удалении точки M кривой от начала
координат расстояние от точки
M
до прямой
ℓ
стремится к нулю.
Замечание.
Выделяют два вида асимптот: вертикальные и наклонные.
Вертикальные асимптоты кривая y = f(x) не пересекает,
наклонные – может пересекать.

66.

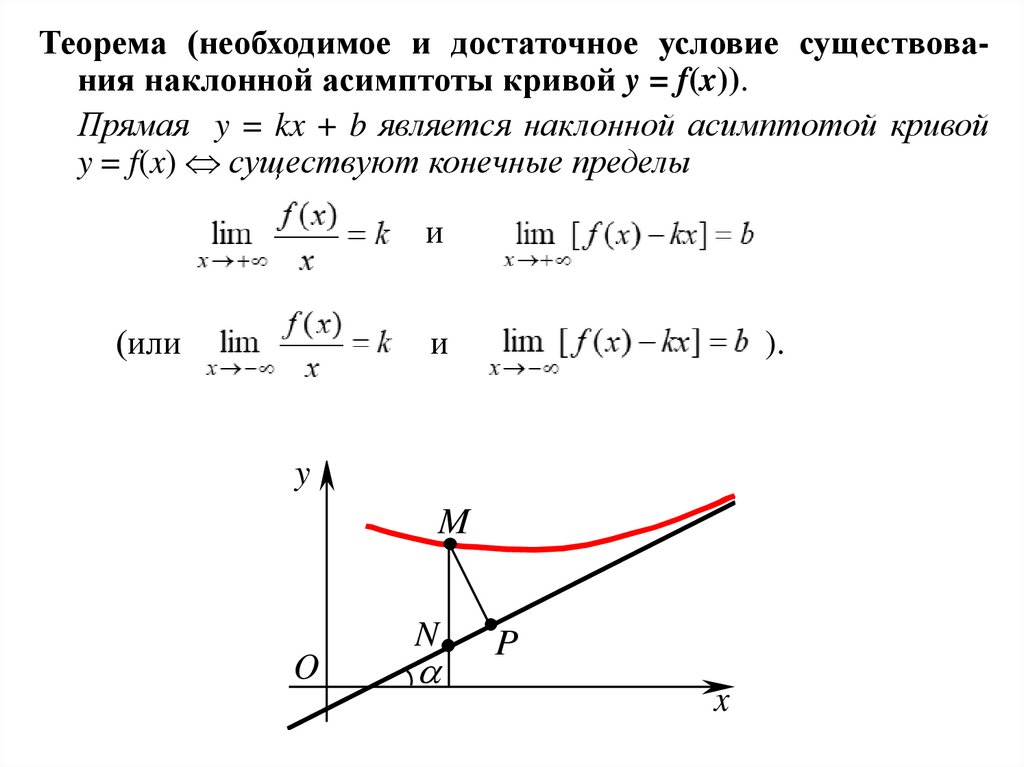
Теорема (необходимое и достаточное условие существования наклонной асимптоты кривой y = f(x)).
Прямая y = kx + b является наклонной асимптотой кривой
y = f(x) существуют конечные пределы
и
(или
и
).
y
M
N
O
P
x

67.

Замечания.
1. Наклонных асимптот у кривой y = f(x) может быть не более
двух: для правой ветви (т.е. при x + ) и для левой ветви
(т.е. при x – ).
2. Если
и
,
то наклонная асимптота имеет уравнение y = b, т.е. является
горизонтальной.

68.

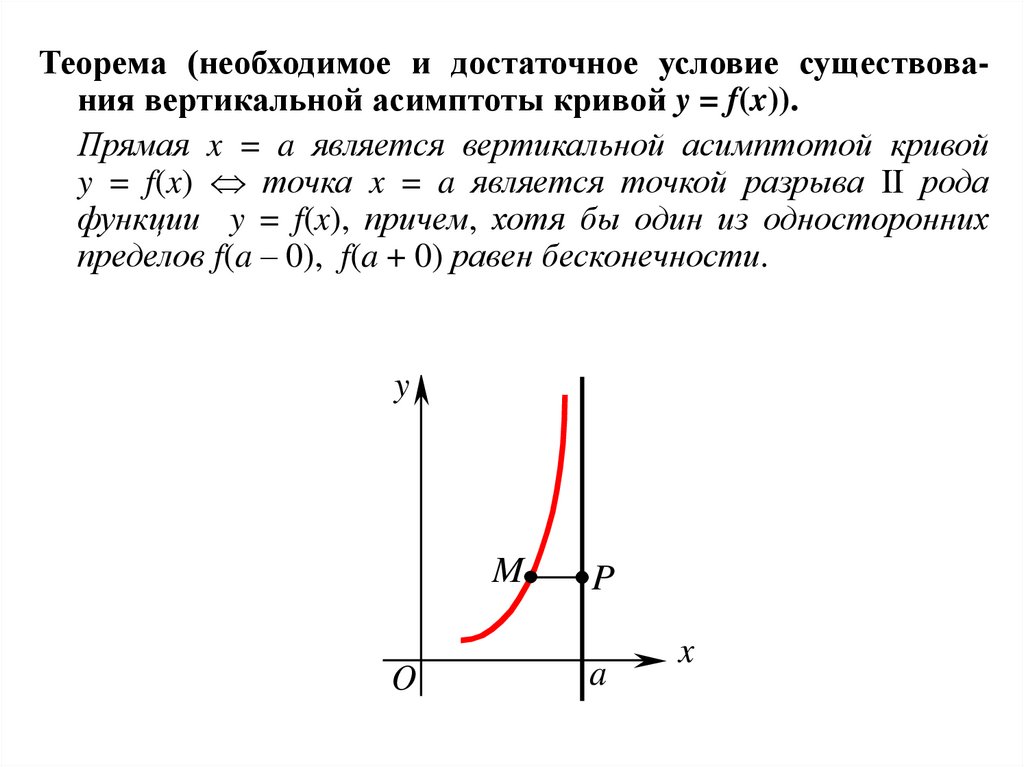
Теорема (необходимое и достаточное условие существования вертикальной асимптоты кривой y = f(x)).
Прямая x = a является вертикальной асимптотой кривой
y = f(x) точка x = a является точкой разрыва II рода
функции y = f(x), причем, хотя бы один из односторонних
пределов f(a – 0), f(a + 0) равен бесконечности.
y
M
O
P
a
x

69. СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ

1. Найти область определения функции.
2. Найти точки пересечения графика с осями координат.
3. Исследовать четность (нечетность) и периодичность функции.
4. Исследовать точки разрыва, найти вертикальные асимптоты.
5. Найти наклонные асимптоты (если они существуют).
6. Найти f (x). Определить точки экстремума, интервалы возрастания и убывания функции.
7. Найти f (x). Определить точки перегиба графика, интервалы
его выпуклости и вогнутости.
8. Построить график функции.