Идеальные растворы. Законы Дальтона и Рауля

1. Идеальные растворы. Законы Дальтона и Рауля

2.

Модельная
система:
идеальный
жидкий
бинарный раствор в равновесии с собственным
паром. Растворитель («1») и растворенное
вещество («2») летучи, пар над раствором
содержит оба компонента и имеет свойства
идеального газа.
Р = Р1 + Р 2
(1)
Закон Дальтона: парциальное давление Рi газа в
смеси пропорционально общему давлению Р и
мольной доле этого газа в газовой фазе хi
Pi Pxi
П
(2)

3. В идеальных растворах стремление к переходу в газовую фазу одинаково для всех компонентов раствора и связано с концентрацией компонента в

растворе.
Закон Рауля: парциальное давление пара i-того
компонента Pi пропорционально его мольной доле в
растворе xi и давлению насыщенного пара чистого
компонента Pi0
(3)

4. Если оба компонента идеального раствора летучи, то закон Рауля выполняется для каждого из них на всем интервале концентраций, а общее давл

Если оба компонента идеального раствора летучи, то закон
Рауля выполняется для каждого из них на всем интервале
концентраций, а общее давление пара над раствором равно
сумме парциальных давлений компонентов. Все зависимости
давление - состав линейны.
P1 P1 x1
Ж
(4)
P2 P2 x2
(5)
0
0
Ж
P Р1 Р2 Р1 x1 Р2 x2
0
Р2 ( Р1 Р2 ) x1
0
0
0
0
(6)

5.

Для бинарного раствора, образованного нелетучим растворенным
веществом и летучим растворителем:
P1 P1 x1 Р1 1 х 2
0
0
Р1 Р1 Р
0 x2
0
Р1
Р1
0
(7)
Oтносительное понижение давления пара растворителя над
раствором равно мольной доле растворенного вещества.
Для разбавленных растворов электролитов:
Р
in2
in2
n2 n1
0
Р1
n1 n2 n1
i – изотонический коэффициент Вант-Гоффа
i 1 ( 1)

6. Предельно (бесконечно) разбавленные растворы. Закон Генри.

В предельно разбавленных растворах к растворителю
применимы законы
идеальных растворов (закон
Рауля), а для растворенного вещества справедлив
закон Генри.
Парциальное давление пара растворенного
вещества
над
бесконечно
разбавленным
раствором пропорционально его мольной доле в
растворе.

7.

Закон Генри применим только к растворенному веществу
и только в предельно разбавленном растворе.
Р2 K Г x2
(8)
КГ (Г) – константа Генри.
В идеальных растворах:
P2 P2 x2 К Г Р2
0
0
P2
tg
KГ
x2

8. Реальные растворы. Отклонения от закона Рауля.

С ростом давления пара
или концентрации
раствора наблюдаются
положительные и
отрицательные
отклонения от закона
Рауля.

9. Положительные отклонения от закона Рауля

1)
Положительные отклонения от закона Рауля
Взаимодействия между частицами в реальном растворе слабее,
чем в идеальном растворе: ∆Р = РРЕАЛ – РИД > 0; ∆H > 0; ∆V > 0

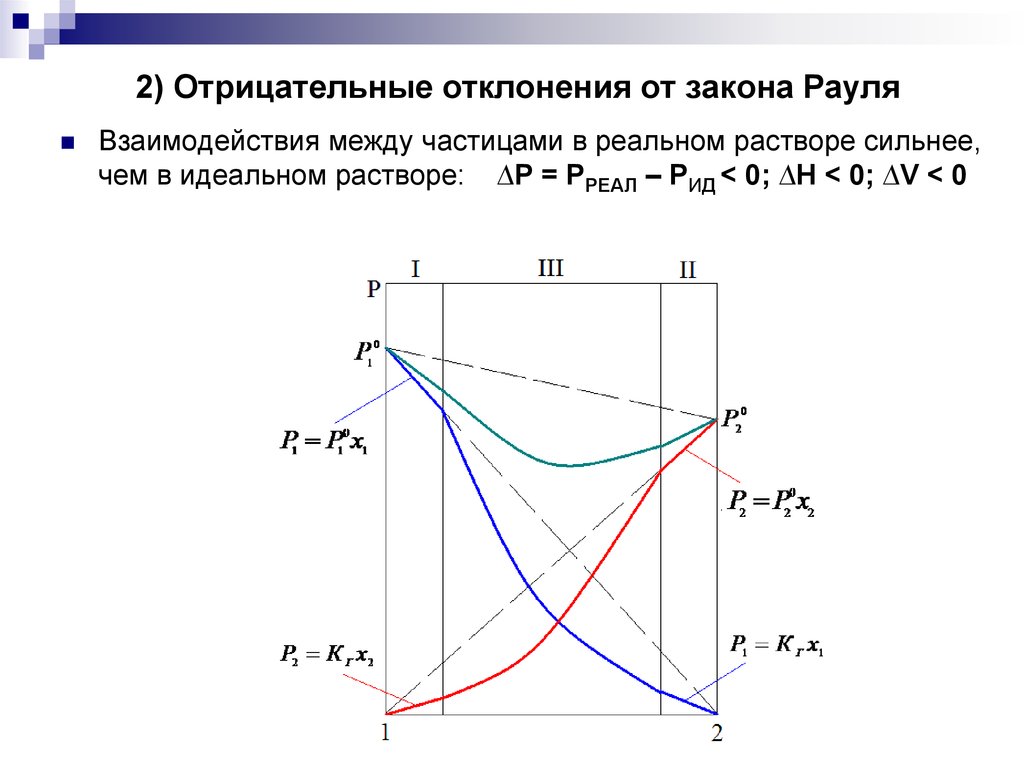
10. 2) Отрицательные отклонения от закона Рауля

Взаимодействия между частицами в реальном растворе сильнее,
чем в идеальном растворе: ∆Р = РРЕАЛ – РИД < 0; ∆H < 0; ∆V < 0

11. Термодинамика реальных растворов. Активность и коэффициент активности

Для описания свойств реальных систем Льюис ввел в
термодинамику растворов понятие активности i-того
компонента для конденсированных растворов и
фугитивности или летучести для газовых растворов.

12.

Активность (аi) – эффективная или реально действующая
концентрация компонента в растворе
ai Ci i
i
Фугитивность (fi) – эффективное давление пара
fi Pi i
коэффициент
активности
(фугитивности);
является
поправочным коэффициентом, учитывающим различие в
межмолекулярных взаимодействиях для молекул разной
природы.
В идеальном растворе
i 1 ai Ci и fi Pi
i 1
- положительные отклонения от закона Рауля
i 1
- отрицательные отклонения от закона Рауля

13. Активность – гипотетическая величина, которая при подстановке вместо концентрации в уравнения для идеальных растворов позволяет использ

Активность – гипотетическая величина, которая
при
подстановке
вместо
концентрации
в
уравнения для идеальных растворов позволяет
использовать
их
для
описания
реальных
растворов
и
получать
сопоставимые
результаты эксперимента и расчета.
Абсолютная величина активности и коэффициента
активности зависит от способа выражения концентрации
раствора
x c m ; ax ac am
В бесконечно разбавленных растворах
( x c m ) 1

14.

Идеальный раствор
Реальный раствор
i i RT ln Pi
i i RT ln f i
i i RT ln хi
i i RT ln аi
0
0
0
0
0
0
Р1 Р1 Р
f
f
f
Р
Р
Р
1
1
1
1
0 x2
0 x2
0 а2
0
0
0
Р1
Р1
f1
f1
Р1
Р1
0
P2 К Г x2
P2 К Г а2