Раздел 3. Аналитическая геометрия. Глава 1. Аналитическая геометрия на плоскости. Тема 1. Системы координат на плоскости

1.

РАЗДЕЛ 3.
АНАЛИТИЧЕСКАЯ
ГЕОМЕТРИЯ
Глава 1. Аналитическая
геометрия на плоскости
§1. Системы координат на
плоскости

2.

1.1 ПРЯМОУГОЛЬНАЯ СИСТЕМА
КООРДИНАТ НА ПЛОСКОСТИ
Выберем
на
плоскости
две
взаимно
перпендикулярные прямые OX и OY с
указанными
на
них
положительными
направлениями. Прямые OX и OY называют
координатными
осями,
точку
их
пересечения О – началом координат.
Выберем
также
единицу
масштаба
–
единичный отрезок.

3.

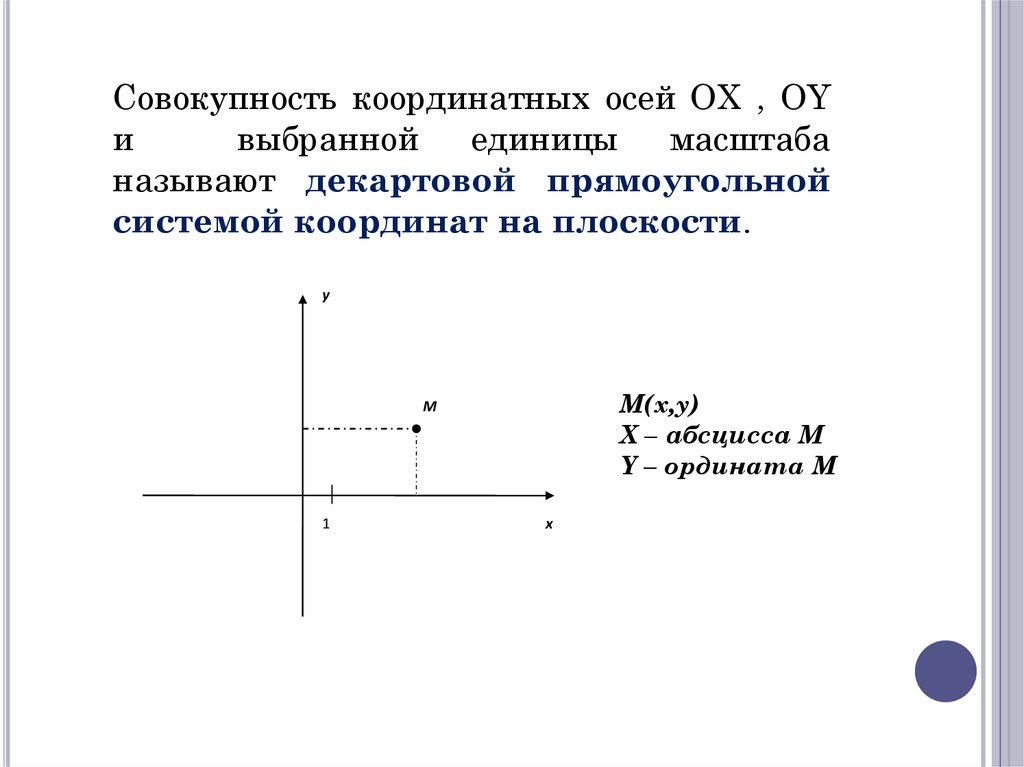
Совокупность координатных осей OX , OY
и
выбранной
единицы
масштаба
называют декартовой прямоугольной
системой координат на плоскости.
y
М(x,y)
X – абсцисса М
Y – ордината М
M
1
x

4.

1.2 ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ
НА ПЛОСКОСТИ
Зафиксируем на плоскости точку P и выходящую из нее
прямую PO, выберем единицу масштаба. Точку P назовем
полюсом, луч PO – полярной осью.
Произвольной точке M плоскости поставим в
соответствие два числа:
полярный радиус r – расстояние от точки M до
полюса P;
полярный угол - угол между полярной осью PO и
полупрямой PM.
M
P
O

5.

Рассмотрим декартову систему координат, у которой
начало координат точка O совпадает с полюсом
полярной системы – точкой P.
y
М
y
x
P
x

6.

§2. УРАВНЕНИЯ ПРЯМОЙ НА ПЛОСКОСТИ
Уравнением
линии на плоскости в
прямоугольной
системе
координат
называется
уравнение
,
которому
удовлетворяют координаты каждой точки
этой
линии
и
не
удовлетворяют
координаты любой точки плоскости, не
лежащей на этой линии.

7.

2.1. УРАВНЕНИЕ ПРЯМОЙ С УГЛОВЫМ
КОЭФФИЦИЕНТОМ
Рассмотрим
на
плоскости
прямоугольную систему координат
XOY и прямую L, которая отсекает по
оси OY отрезок OB=b.
k tg
- угловой коэффициент
прямой.
Пусть M x, y - произвольная точка
прямой.

8.

Из рисунка видно, что
y b
k tg
y b kx
x
y kx b (1) - уравнение прямой с
угловым коэффициентом.

9.

2.2 УРАВНЕНИЕ ПРЯМОЙ, ПРОХОДЯЩЕЙ
ЧЕРЕЗ ДАННУЮ ТОЧКУ С ДАННЫМ
УГЛОВЫМ КОЭФФИЦИЕНТОМ
Рассмотрим
на
плоскости
прямоугольную систему координат XOY и
прямую L, которая проходит через точку
M1 x1; y1 .
k tg
прямой.
-
угловой
коэффициент

10.

Пусть M x, y - произвольная точка
прямой. M1 x1; y1 - фиксированная (данная)
точка прямой.
Из рисунка видно, что
k tg
y1 y
k x1 x y1 y y y1 k x x1
x1 x
(2)
- уравнение прямой, проходящей через
точку M x ; y с угловым коэффициентом k.
1
1
1

11.

2.3. УРАВНЕНИЕ ПРЯМОЙ ПО ДВУМ
ТОЧКАМ
Рассмотрим
на
плоскости
прямоугольную систему координат
XOY и прямую L, которая проходит
через точки M1 x1; y1 и M 2 x2 ; y2 .

12.

Из рисунка видно, что k tg
y2 y1
x2 x1
.

13.

Подставим найденный угловой коэффициент
в уравнение (2). Получим:
y2 y1
y2 y1
y
x x1
x x1 y1 y y1
x2 x1
x2 x1
x x1
y y1
x2 x1 y2 y1 (3) - уравнение прямой,
проходящей через точки M1 x1; y1 и M 2 x2 ; y2 .

14.

2.4. ОБЩЕЕ УРАВНЕНИЕ ПРЯМОЙ
Общее уравнение прямой имеет вид:
Ax By C 0 (4).
1. Если A 0 , B 0 , тогда уравнение (4)
By C 0 y
C
B
примет вид:
- прямая
параллельна оси OX.
2. Если B 0 , A 0 , тогда уравнение (4)
C
Ax
C
0
x
примет вид:
- прямая
A
параллельна оси OY.

15.

3. Если A C 0 , B 0 , тогда уравнение (4)
примет вид: By 0 y 0 - прямая
совпадает с осью OX.
4. Если B C 0 , A 0 , тогда уравнение
(4) примет вид: Ax 0 x 0 - прямая
совпадает с осью OY.
5. Если C 0 , A 0 , B 0 тогда уравнение
(4) примет вид: Ax By 0 - прямая
проходит через точку О(0,0).

16.

2.5. УРАВНЕНИЕ ПРЯМОЙ «В ОТРЕЗКАХ»
Рассмотрим
уравнение
A 0, B 0, C 0 .
(4)
Ax By C 0 ,
Ax By C 0 Ax By C |: C 0
.
Обозначим
Тогда
отрезках».
C
a,
A
A
B
x
y 1
C
C
C
b .
B
x
y
1 - уравнение прямой «в
a b

17.

§ 3. УГОЛ МЕЖДУ ПРЯМЫМИ
Рассмотрим прямые:
L1 : y k1 x b1 , L2 : y k2 x b2
Пусть
они
пересекаются
некоторым углом . Тогда
k1 k2
tg
1 k1k2
.
под

18.

Частные случаи формулы (1).
1. Пусть L1 // L2 , тогда
,
k1 k2
tg tg 0
0 k1 k2 0
1 k1k2
k1 k2 - условие параллельности двух
прямых.

19.

2. Пусть L1 L2 , тогда
дробь
k1 k2
1 k1k2
, значит
теряет арифметический смысл.
1 k1k2 0 k1k2 1 - условие
перпендикулярности двух прямых.