Автоматика и управление. Тема 5. Устойчивость линейных стационарных автоматических систем

1.

Автоматика и управление
Тема 5. Устойчивость линейных
стационарных автоматических
систем
ПЗ 7. Определение устойчивости ЛСС с
использованием алгебраических критериев.

2.

Задача № 1
Оценить устойчивость продольного движения
самолета, если характеристическое уравнение имеет вид:
0,7р3+20р2+р+0,1=0.
Решение:
1 .Необходимое условие выполняется ?
2. Т.к. система третьего порядка, то воспользуемся правилом
Вышнеградского:
a1 a2 a0 a3 ;
1 20-0,1 0,7 0
АС – устойчива

3.

Задача № 2.
Структурная схема АС имеет вид:
Х(р)
1
0 ,05 p 1
0 ,5 p 1
0 ,1 p 1
50
p2
Y(р)
С помощью критерия Гурвица исследовать устойчивость
замкнутой АС.
Решение: 1 .Чтобы исследовать устойчивость необходимо получить
характеристический полином системы
W(p)=
50( 0 ,5 р 1 )
25 р 50
;
2
4
3
2
( 0 ,05 р 1 )( 0 ,1 р 1 ) р
0 ,005 р 0 ,15 р р
Ф(р)=
W ( p)
25 р 50
В( р )
;
1 W ( p) 0 ,005 р 4 0 ,15 р 3 р 2 25 р 50 А( р )
A(p)=0,005р4+0,15р3+р2+25р+50 – характеристический полином
Необходимое условие выполняется, в структуре системы признаков
неустойчивости нет

4.

3. Составим матрицу Гурвица из коэффициентов
характеристического полинома:
A(p)=0,005р4+0,15р3+р2+25р+50
R=
50
0
0
0
1
25
50
0
0 ,005 0 ,15
1
25
0
0
0 ,005 0 ,15
Вычислим определители подматриц матрицы Гурвица R:
Δ1=detR1=0,15 >0
1
25
1 0 ,15 0 ,005 25 0
Δ2=detR2=
0 ,005 0 ,15
25
50
0
Δ3=detR3= 0 ,15 1
25 = -0,5<0
0
0 ,005 0 ,15
АС неустойчива

5.

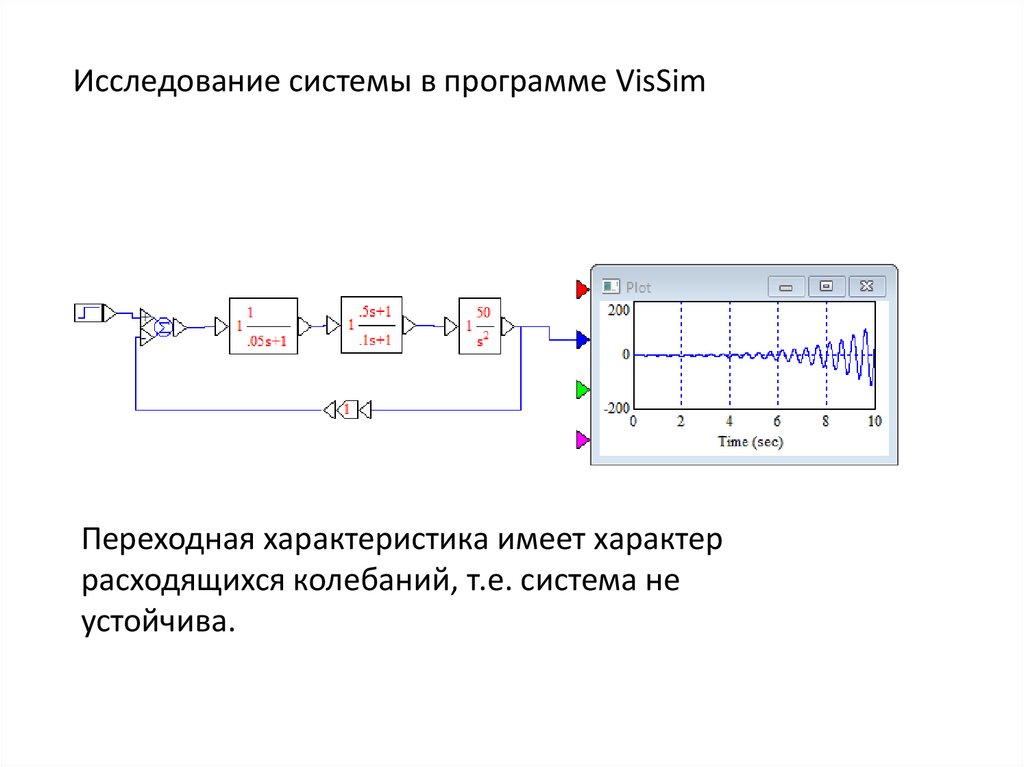
Исследование системы в программе VisSim
Переходная характеристика имеет характер
расходящихся колебаний, т.е. система не
устойчива.

6.

Задача №3
Передаточная функция разомкнутой системы имеет вид:
W( p )
0 ,1К ( р 1 )
р( 5 р 1 )( 3 р 1 )
Используя критерий Гурвица найти критическое значение
коэффициента усиления разомкнутой системы.
1. Определим передаточную функцию замкнутой АС:
W ( p)
0 ,1К ( р 1 )
0 ,1Кр 0 ,1К
;
Ф(р) =
3
2
1 W ( p)
р( 5 р 1 )( 3 р 1 ) 0 ,1К ( р 1 ) 15 р 8 р ( 1 0 ,1К ) р 0 ,1К
А(р)=15р3+8р2+(1+0,1К)р+0,1К
2. Критический коэффициент усиления соответствует нахождению АС на
границе устойчивости.
Анализ соответствия коэффициентов А(р) необходимому условию
устойчивости
Ккр>0
1+0.1Ккр>0

7.

Учитывая, что а0 0, воспользуемся критерием Гурвица для АС находящейся на
границе устойчивости.
det R=a0 Rn 1 =0
0 ,1К
R= 8
0
0
1 0 ,1К
15
0
0 ,1К
8
det Rn-1=0
R2
Из условия detR2=0 определим Ккр:
(1+0,1К)8-15 0,1К=0
(1+0,1К)8=15 0,1К
Ккр 11,43
АС будет устойчива при коэффициенте усиления разомкнутой системы
0 К 11,43.

8.

Методика оценки устойчивости по критерию
Гурвица:
1. Проверить
выполнение
необходимого
условия устойчивости по коэффициентам А(р).
2.
Составить
матрицу
Гурвица
из
коэффициентов А(р) замкнутой системы.
3. Определить знаки определителей подматриц
матрицы Гурвица.
4. Если хотя бы один из определителей
отрицателен – система неустойчива. В противном
случае – устойчива.

9.

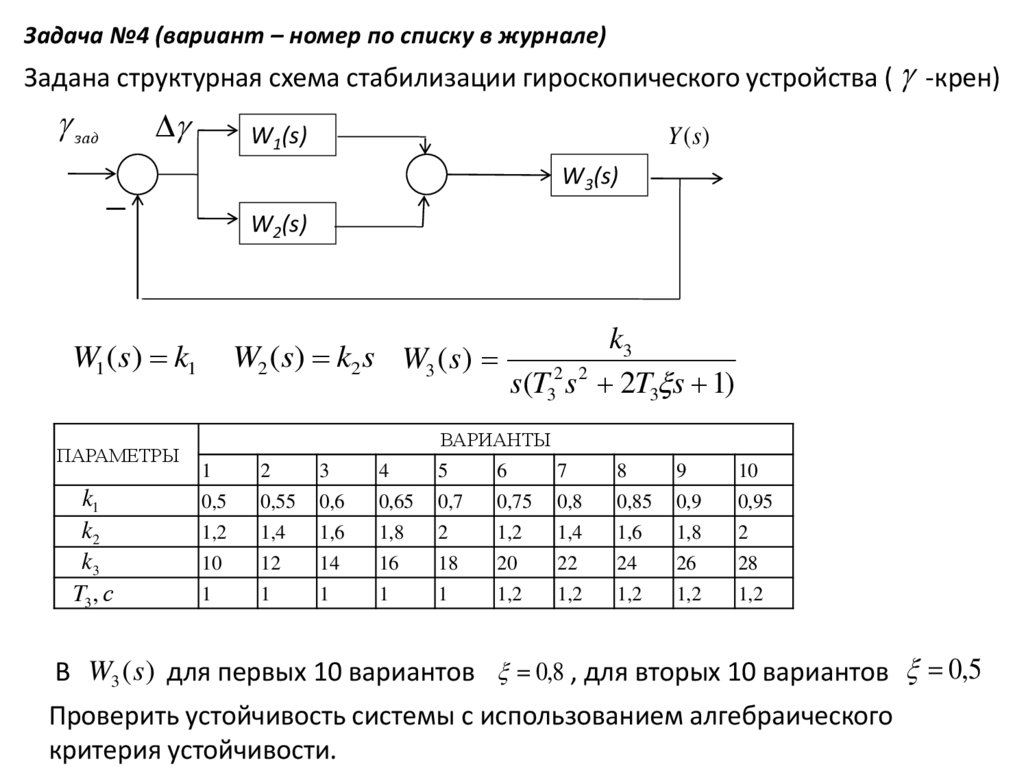
Задача №4 (вариант – номер по списку в журнале)
Задана структурная схема стабилизации гироскопического устройства ( -крен)
зад
W1(s)
W3(s)
W2(s)
W1 (s) k1
ПАРАМЕТРЫ
k1
k2
k3
T3 , с
Y (s)
W2 (s) k2 s W3 ( s)
k3
s(T32 s 2 2T3 s 1)
ВАРИАНТЫ
1
2
3
4
5
6
7
8
9
10
0,5
0,55
0,6
0,65
0,7
0,75
0,8
0,85
0,9
0,95
1,2
1,4
1,6
1,8
2
1,2
1,4
1,6
1,8
2
10
12
14
16
18
20
22
24
26
28
1
1
1
1
1
1,2
1,2
1,2
1,2
1,2
В W3 ( s) для первых 10 вариантов 0,8 , для вторых 10 вариантов 0,5
Проверить устойчивость системы с использованием алгебраического
критерия устойчивости.