Теорія границь

1.

Лекція №5
Тема Теорія границь
План
1. Нарахування простих та складних процентів.
2. Числова послідовність. Границя числової
послідовності.
3. Границя функції в точці. Односторонні границі.
4. Нескінченно малі і нескінченно великі величини.

2.

Нарахування простих процентів
Нехай на початкову суму (теперішня величина
грошових коштів) PV нараховують річну процентну
ставку i.
Тоді майбутня величина грошових коштів FV
становитиме:
- на кінець першого інтервалу
нарахувань
-на кінець другого інтервалу
нарахувань
-на кінець n-го інтервалу
нарахувань

3.

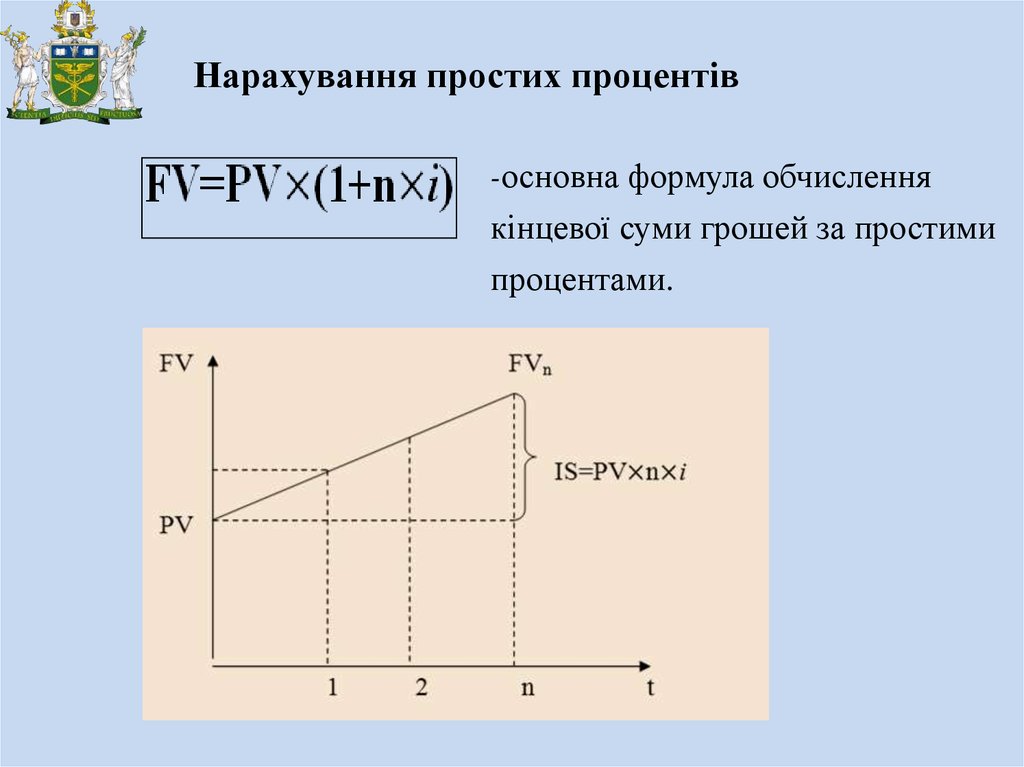
Нарахування простих процентів
-основна формула обчислення
кінцевої суми грошей за простими
процентами.

4.

Нарахування складних процентів
Приклад 1
Петро Клименко хоче дати в борг на один рік 1 млн.
грн. під 9% річних. В кінці першого року йому
нарахують суму (у млн. грн):
Петро може забрати нараховані проценти, а може
залишити ще на рік.Петро вибирає другий варіант.
В кінці другого року йому нараховують :
Відповідно в кінці третього року:

5.

Нарахування складних процентів
Приклад 1 (продовження)
В кінці n-го року Необхідно звернути увагу на слідуюче:
- нарахування за простими
процентами на початкову
суму
-нарахування процента
на процент.
Метод підрахунку майбутньої вартості, коли нарощену за
кожний інтервал суму знову вкладають під простий
процент, називають правилом складних процентів
Результат нарахування - складними процентами .

6.

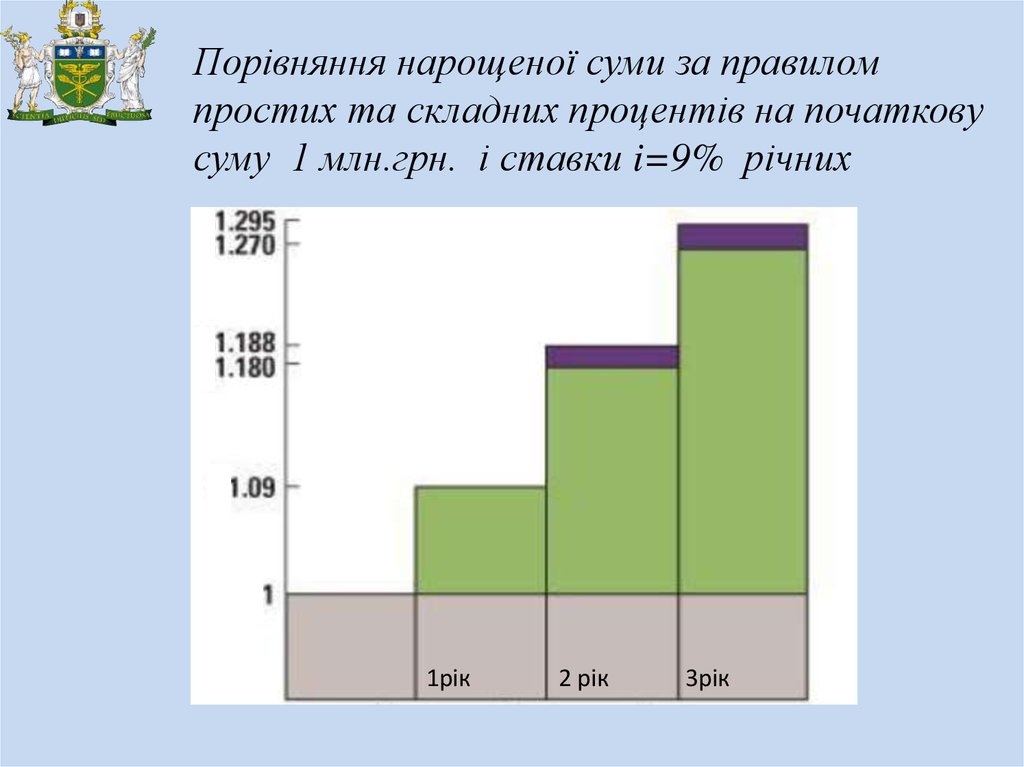
Порівняння нарощеної суми за правилом
простих та складних процентів на початкову
суму 1 млн.грн. і ставки i=9% річних
1рік
2 рік
3рік

7.

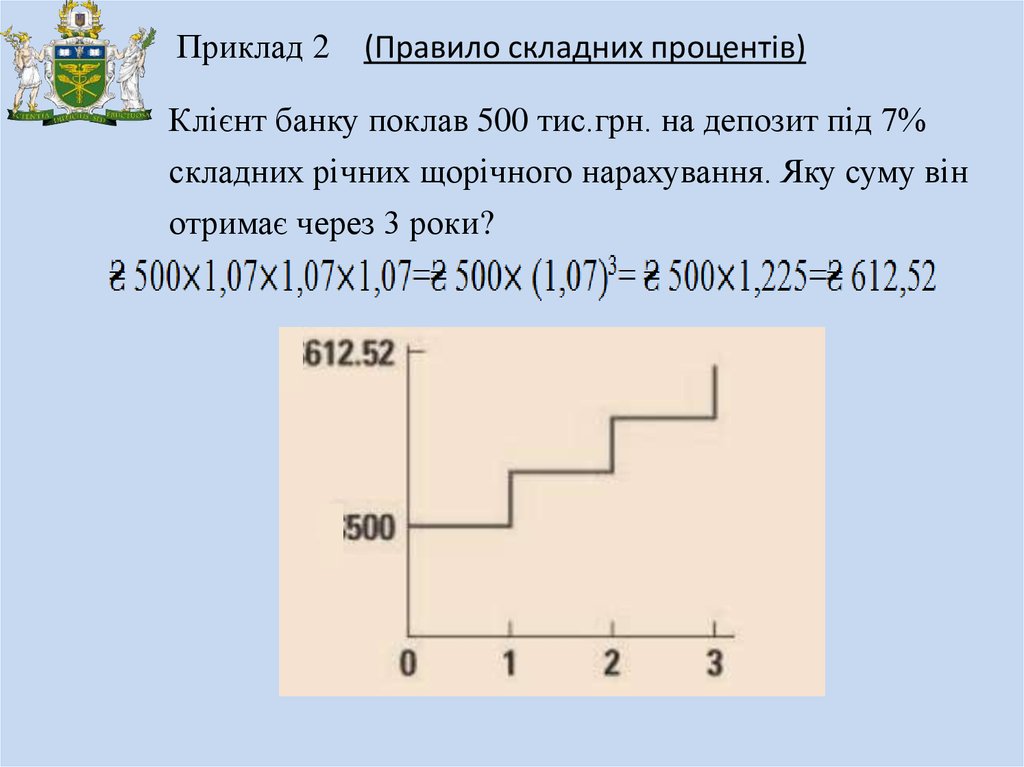
Приклад 2
(Правило складних процентів)
Клієнт банку поклав 500 тис.грн. на депозит під 7%
складних річних щорічного нарахування. Яку суму він
отримає через 3 роки?

8.

Нарахування складних процентів
Отже, в загальному вигляді нарощена сума
буде змінюватись за правилом:
формула нарощування за
складними процентами
множник нарощування
складних процентів
Для коректних обчислень величини i та n
мають бути узгоджені.

9.

Нарахування складних процентів
У випадку, якщо відсотки нараховуються m разів на
рік, відсоток за період
року складає
де i- річна процентна ставка
i nm
FV PV (1 )
m

10.

Нарахування складних процентів
Розглянемо випадок, коли кількість нарахувань
необмеженно збільшується, тобто прямує до
нескінченності (неперервне нарахування ) .
Приймемо також до уваги, що для виразу де змінна
величина прямує до відомої границі прийнято
використовувати символ lim.
Тоді формула нарахування складних процентів при
неперервному нарахуванні процентів прийме
вигляд:

11.

Числова послідовність
Означення 1. Величину називають змінною,
якщо вона набуває різних значень під час
розв’язування задачі, в протилежному випадку
величина – стала.
Позначення : x, y, z,.. – змінні; a, b, c,.. - сталі
Означення 2. Змінну х називають впорядкованою
змінною або числовою послідовністю, якщо
відома сукупність усіх її можливих значень і про
кожне можна сказати, яке попереднє, а яке наступне,
тобто значення змінної величини можна за певним
правилом занумерувати.
Позначення : xn , yn , zn .

12.

Числова послідовність. Границя числової
послідовності
Приклади числових послідовностей
Іншими словами:
Числова послідовність - це функція натурального
аргумента yn = f (n).
Якщо із збільшенням номера n значення f (n)
необмеженно наближаються до деякого числа а, то
кажуть, що число а є границею числової
послідовності yn = f (n) і записують:

13.

Числова послідовність. Границя числової
послідовності.
Означення 3.
Число а називають границею числової послідовності
хn , якщо для всякого наперед заданого як завгодно
малого числа ɛ >0, існує такий номер N, що для
всіх n >N виконується нерівність | хn - а | < ɛ
Геометричний зміст
2ɛ
а- ɛ
х2 х4
а
а+ ɛ
х25 х26 …. xm…
.
х3
х1
хn

14.

Числова послідовність. Границя числової
послідовності.
Приклад 3.
Показати, що змінна величина (числова
послідовність)
хn =2+1/1, x2=2+ 1/2 , …. . xn = 2+ 1/n , …. має
границю,
а=2.
Розвязок
Дійсно, | хn - 2 | = | (2 +1/n ) -2| =1 /n,
і для будь-якого ɛ можна вказати номер N =1/ɛ
такий, що для всіх наступних n> N
виконуватиметься нерівність
| хn - 2 | = 1 /n <1/1/ɛ = ɛ . Отже,

15.

Границя функції в точці..
Будемо розглядати функцію у =f (x ),визначену в
деякому околі точки А, або в деяких точках цього
околу.
Означення 3.
Число А називають границею у =f (x ), в точці х0 ,
якщо для будь-якого як завгодно малого ɛ >0
знайдеться таке число δ >0 , що для усіх значень
х ≠ х0 ,які задовольняють умову
|х- х0 | <δ , виконується нерівність
|f(x)- A | <ɛ
Позначення:

16.

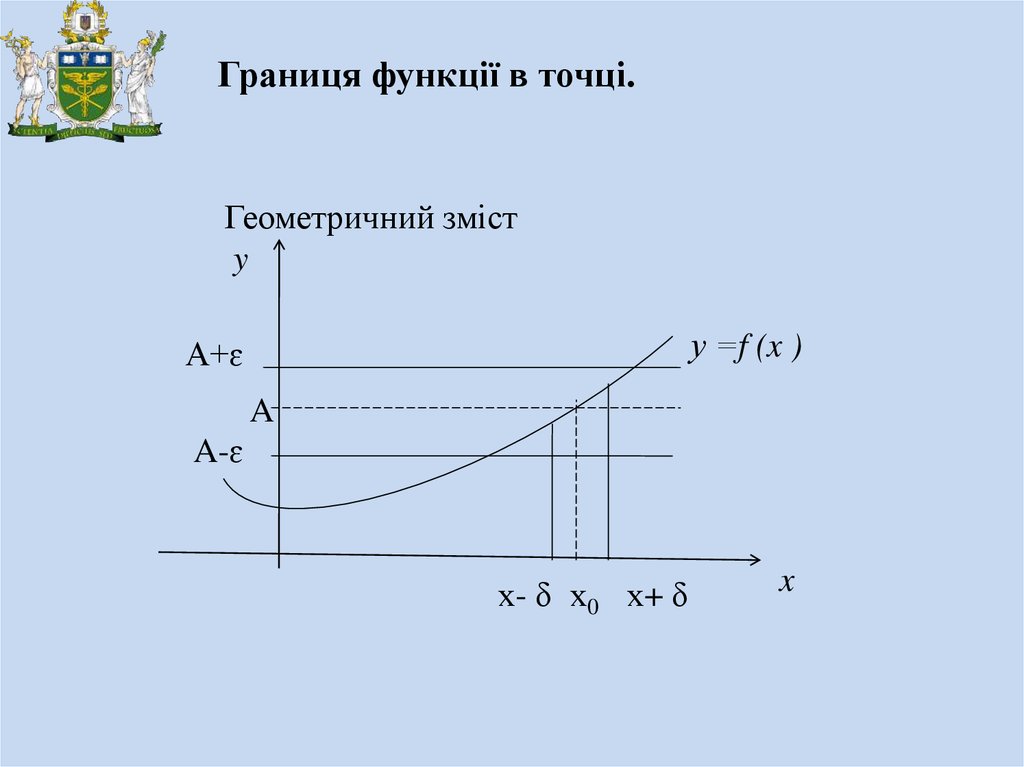
Границя функції в точці.
Геометричний зміст
y
у =f (x )
A+ɛ
A
A-ɛ
х- δ х0 х+ δ
x

17.

Границя функції в точці.
Приклад функціі що не має границі в т. х0
y
y
у =f (x )
у =f (x )
a
b
x0-0
х0
x0 +0
x
x0-0
х0
x0 +0
x

18.

Односторонні границі.
Означення 5
Якшо у =f (x ) прямує до границі А1, коли х прямує
до числа х0 , так що х< х0 , то записують
Якщо у =f (x ) прямує до границі А2 , коли х прямує
до числа х0, так що х > х0 , то записують
Ці границі називають односторонніми, відповідно
ліворуч і праворуч.
Для існування границі А в точці х0, необхідно і
достатньо, щоб існували односторонні границі і
виконувалась рівність А1 = А2 = А

19.

Нескінченно малі величини.
Означення 6.
Функцію y =f (х) називають нескінченно малою
коли х→х0 , або х →∞ , якщо
або
Позначення : Н.М.В. або О (нуль).
Приклади Н.М.В.:
a) y=x2 коли х→ 0 ;
b) у =5/х коли х→ ∞ ;
c) y = 3/(x-4) коли х→ ∞.

20.

Нескінченно великі величини.
Означення 7.
Функцію y =f (х) називають нескінченно великою,
коли х→х0 , або х →∞ ,
якщо
є нескінченно мала величина , коли
х→х0 , або х →∞
Позначення : Н.В.В. або
∞ (нескінченність).
Приклади Н.В.В.:
a) y=1/x2 коли х→ 0 ;
b) у = х+2 коли х→ ∞ ;
c) y = х+3/(x-4) коли х→ 4