Основные элементарные функции (повторение)

1. 3.6. Основные элементарные функции (повторение)

Основными элементарными функциями называют
нижеследующие функции y = f(x).
1. Степенная функция y = x , R. Среди степенных
функций выделяется класс функций с целочисленным
показателем степени: y = xn, n N.
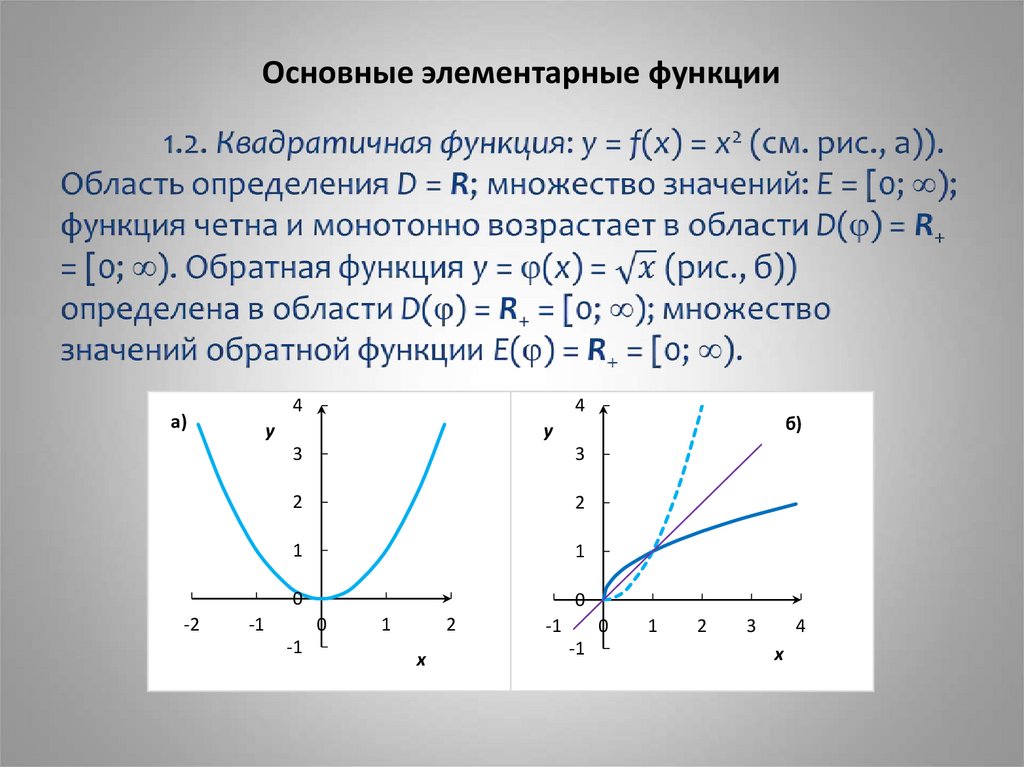
1.1. Линейная функция: y = x (см. рис., а)). Область
определения D = R; множество значений: E = R; функция
нечетна и монотонно возрастает в D. Обратная функция: y =
x (б) совпадает с данной.
б)
2
а)
y2
y
1
1
0
0
-2
-1
0
-1
-2
1
2
x
-2
-1
0
-1
-2
1
x 2

2. Основные элементарные функции

4
а)
-2
4
y
б)
y
3
3
2
2
1
1
0
0
-1
0
-1
1
2
x
-1
0
-1
1
2
3
4
x

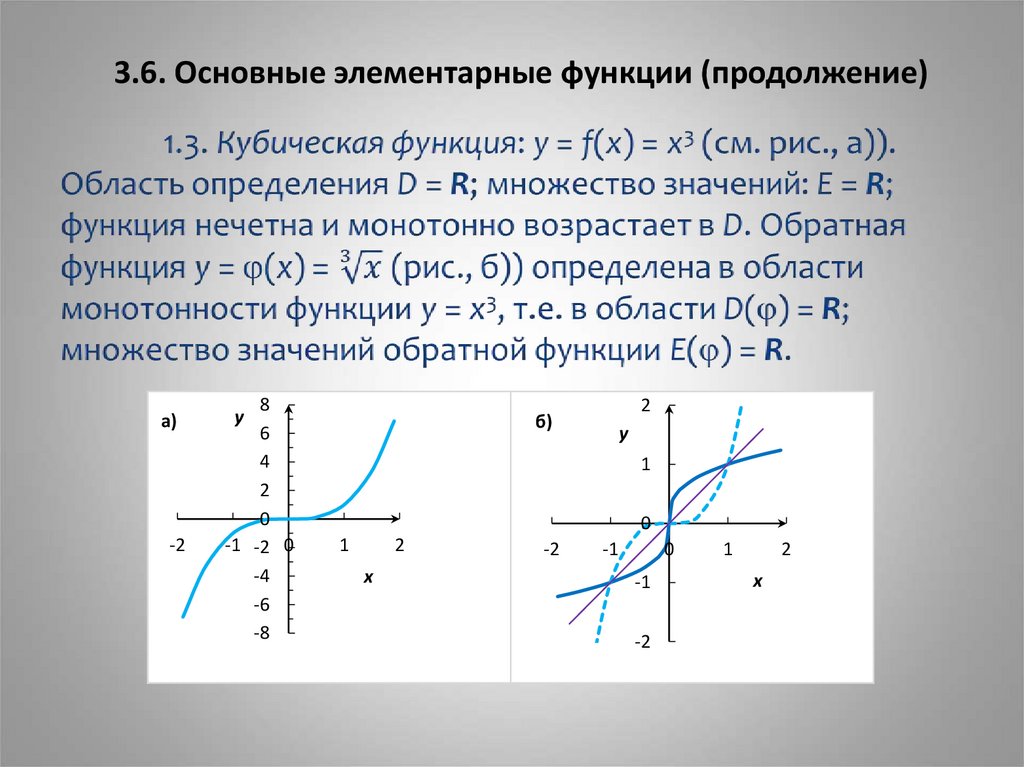
3. 3.6. Основные элементарные функции (продолжение)

а)
-2
8
6
4
2
0
-1 -2 0
-4
-6
-8
y
б)
2
y
1
0
1
2
x
-2
-1
0
-1
-2
1
2
x

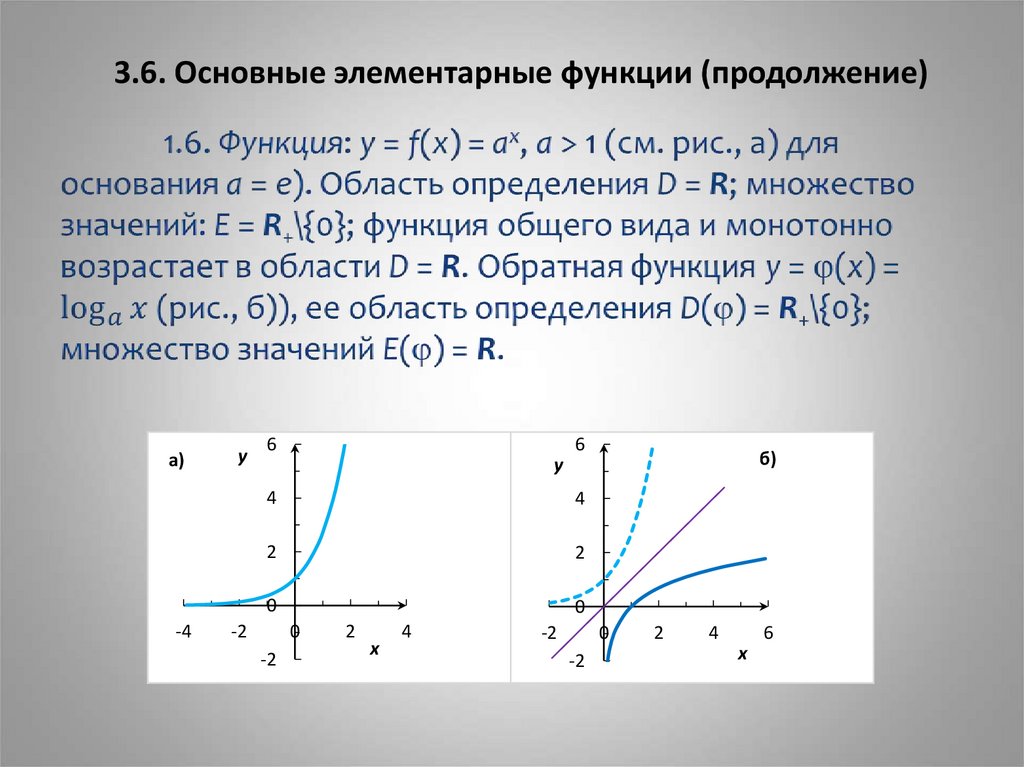
4. 3.6. Основные элементарные функции (продолжение)

а)
-4
y
4
б)
4
y
2
2
0
0
-2
0
-2
-4
2
4
x
-4
-2
0
-2
-4
2
4
x

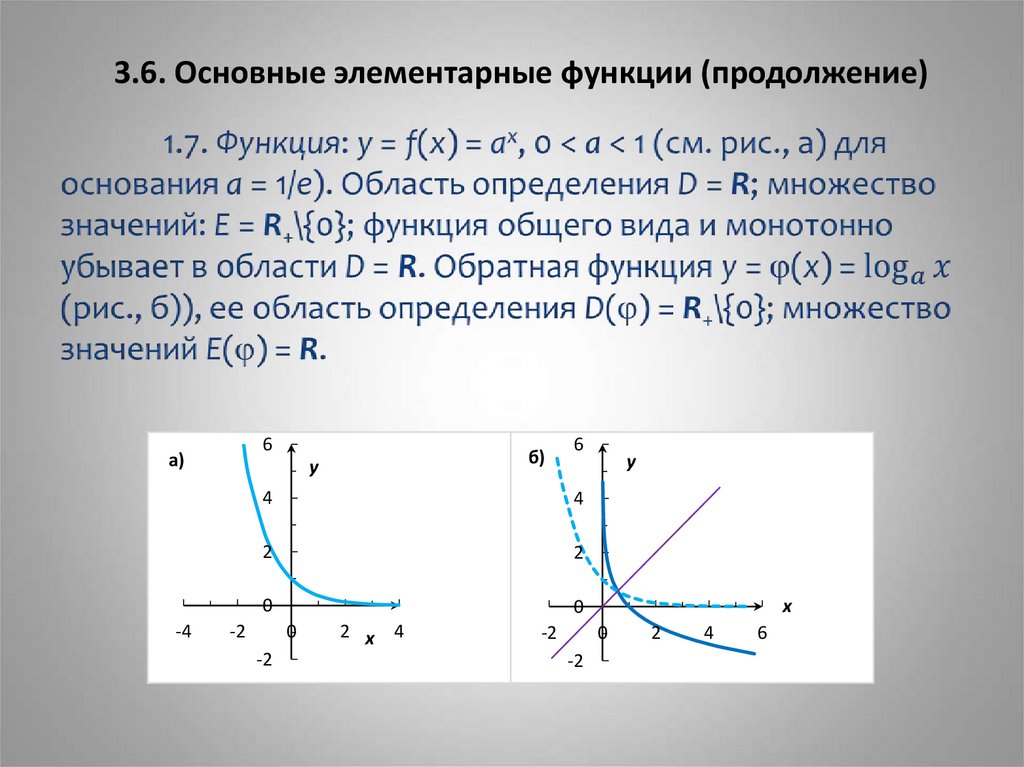
5. 3.6. Основные элементарные функции (продолжение)

а)
-4
y
6
б)
6
y
4
4
2
2
0
0
-2
0
-2
2
4
x
-2
0
-2
2
4
x

6. 3.6. Основные элементарные функции (продолжение)

а)
-4
y
6
6
б)
y
4
4
2
2
0
0
-2
0
-2
2
x
4
-2
0
-2
2
4
6
x

7. 3.6. Основные элементарные функции (продолжение)

6
а)
-4
б)
y
6
4
4
2
2
0
0
-2
0
-2
2 x 4
-2
y
x
0
-2
2
4
6

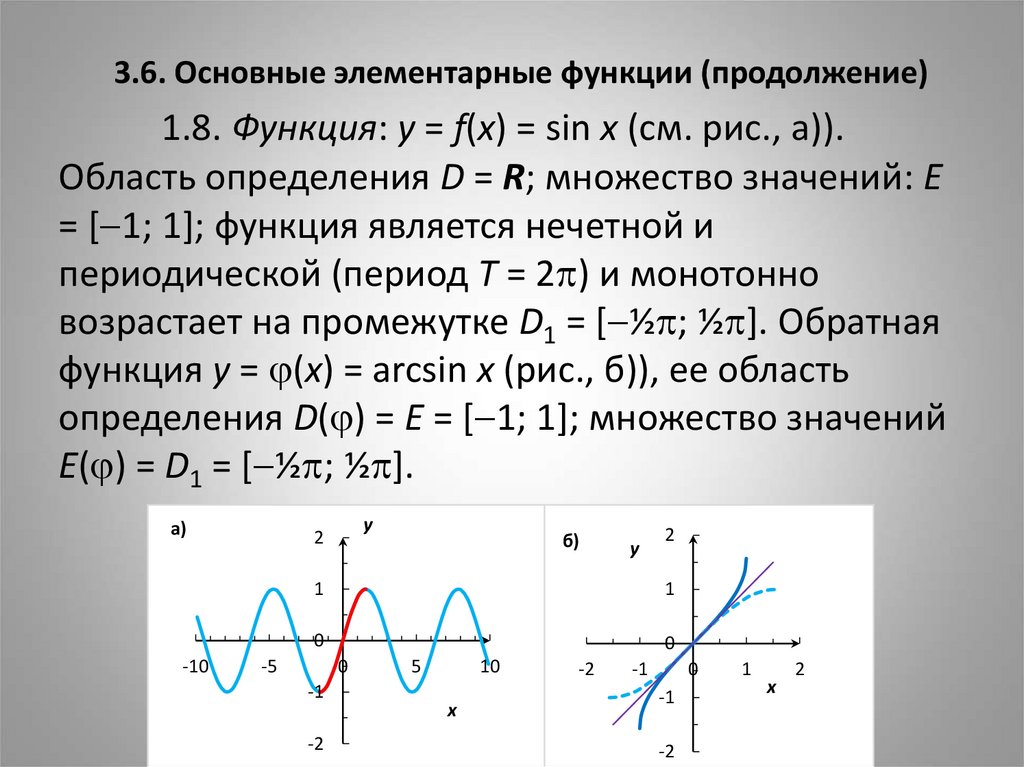
8. 3.6. Основные элементарные функции (продолжение)

1.8. Функция: y = f(x) = sin x (см. рис., а)).
Область определения D = R; множество значений: E
= [ 1; 1]; функция является нечетной и
периодической (период T = 2 ) и монотонно
возрастает на промежутке D1 = [ ½ ; ½ ]. Обратная
функция y = (x) = arcsin x (рис., б)), ее область
определения D( ) = E = [ 1; 1]; множество значений
E( ) = D1 = [ ½ ; ½ ].
а)
-10
y
2
б)
y
2
1
1
0
0
-5
0
-1
-2
5
10
x
-2
-1
0
-1
-2
1
x
2

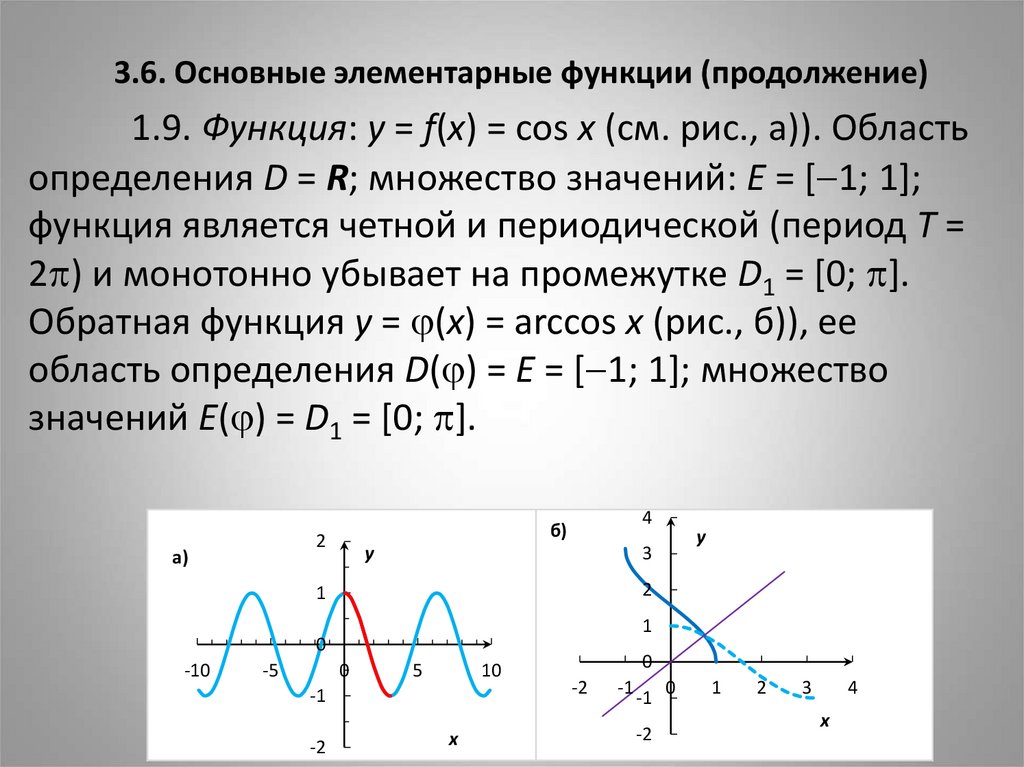
9. 3.6. Основные элементарные функции (продолжение)

1.9. Функция: y = f(x) = cos x (см. рис., а)). Область
определения D = R; множество значений: E = [ 1; 1];
функция является четной и периодической (период T =
2 ) и монотонно убывает на промежутке D1 = [0; ].
Обратная функция y = (x) = arccos x (рис., б)), ее
область определения D( ) = E = [ 1; 1]; множество
значений E( ) = D1 = [0; ].
2
а)
4
б)
y
2
1
1
0
-10
-5
0
5
10
-1
-2
y
3
x
0
-2
-1
-1
-2
0
1
2
3
4
x

10. 3.6. Основные элементарные функции (продолжение)

1.10. Функция: y = f(x) = tg x (см. рис., а)). Область
определения D = R\{ (n + ½), n N}; множество
значений: E = R; функция является нечетной и
периодической (период T = ) и монотонно возрастает
на промежутке D1 = [ ½ ; ½ ]. Обратная функция y =
(x) = arctg x (рис., б)), ее область определения D( ) = E
= R; множество значений E( ) = D1 = [ ½ ; ½ ].
4
а)
4
б)
y
2
2
0
0
-6
-4
-2
0
-2
-4
y
2
4
6
x
-4
-2
0
-2
-4
2
4
x

11. 3.6. Основные элементарные функции (продолжение)

1.11. Функция: y = f(x) = ctg x (см. рис., а)).
Область определения D = R\{ n, n N}; множество
значений: E = R; функция является нечетной и
периодической (период T = ) и монотонно убывает
на промежутке D1 = [0; ]. Обратная функция y = (x)
= arcсtg x (рис., б)), область определения D( ) = E =
R; множество значений E( ) = D1 = [0; ].
4
а)
y
-6
-4
4
б)
2
2
0
0
-2
0
-2
-4
2
4
x
6
-4
-2
y
0
-2
-4
2
4
x

12. 3.5. Сложная функция