Каноническое уравнение гиперболы. Фокусы, асимптоты и директриса гиперболы

1.

Каноническое уравнение
гиперболы.
Фокусы, асимптоты и
директриса гиперболы.

2.

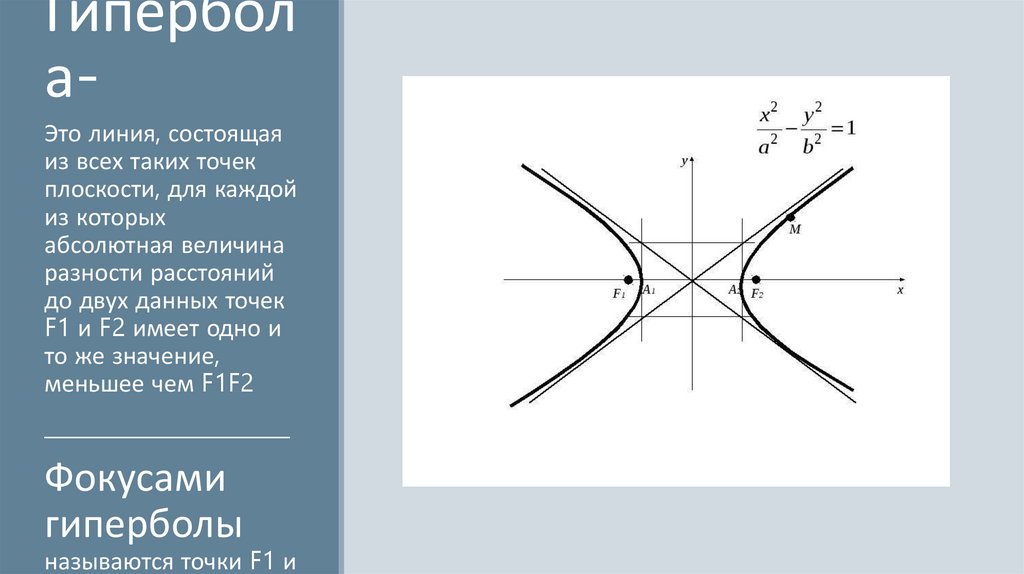
Гипербол
аЭто линия, состоящая
из всех таких точек
плоскости, для каждой
из которых
абсолютная величина
разности расстояний
до двух данных точек
F1 и F2 имеет одно и
то же значение,
меньшее чем F1F2
_______________________
Фокусами
гиперболы
называются точки F1 и

3.

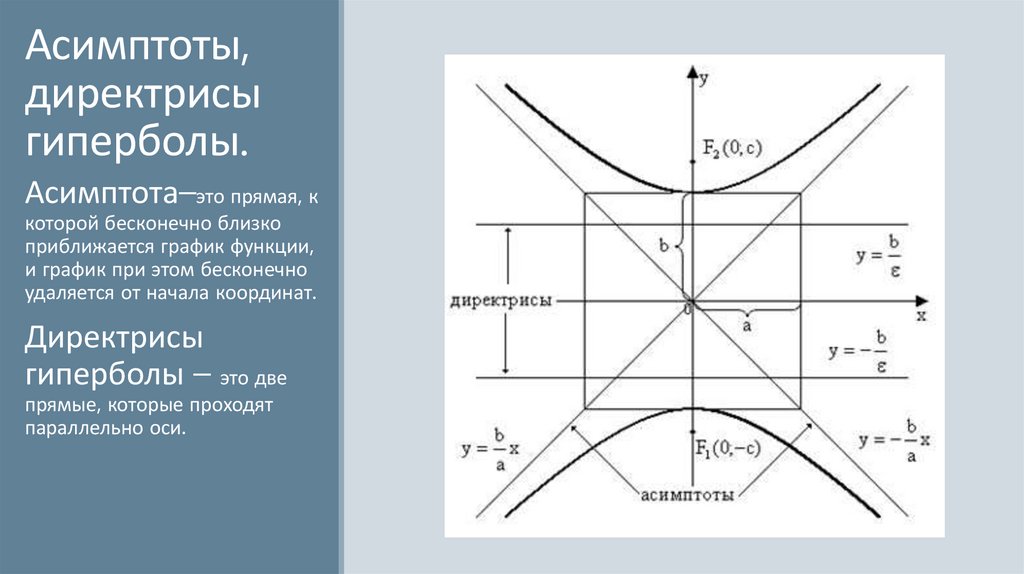
Каноническое уравнение гиперболы.
Доказательство.
Пусть F1F2 = 2с, а постоянную величину, равную
разности расстояний от произвольной точки
гиперболы до ее фокусов обозначим 2а. По
определению гиперболы 2а < 2c, тогда а < c.
Введем систему координат, так, чтобы начало
координат лежало на середине отрезка F1F2, а
точки F1 и F2 лежали на оси абсцисс. Тогда F1(-c;0)
и F2(c;0). Расстояние от произвольной точки М(x;y)
до F1 и F2 выражается формулами MF1 = √