Определители второго порядка

1. Определители

a11 a12
a11 a22 a21 a12
Выражение
a21 a22
называется определителем 2-го
порядка .

2. Определители

Элементы a11 , a 22 называют
элементами главной диагонали
определителя, а другие два элемента –
соответственно элементами побочной
диагонали.

3. Определители третьего порядка

Выражение
a11 a12 a13
a22 a23
a21 a23
a21 a22
a21 a22 a23 a11
a12
a13
a32 a33
a31 a33
a31 a32
a31 a32 a33
называется определителем 3-го
порядка.

4. минор

Минором элемента определителя 3-го
порядка называется определитель 2-го
порядка, получающийся из данного
определителя вычёркиванием строки и
столбца, в которых расположен элемент.

5. Обозначение минора

Минор элемента , стоящего на
пересечении i-й строки и j-го столбца
определителя, обозначают Мij.

6. Алгебраическое дополнение

Алгебраическим дополнением
элемента определителя
3-го
порядка называется минор
этого элемента, взятый со
знаком плюс, если элемент

7. Алгебраическое дополнение (продолжение)

расположен
на
пересечении
строки и столбца
с четной
суммой номеров, и со знаком
минус, если c нечётной.

8. В ы б о р з н а к а

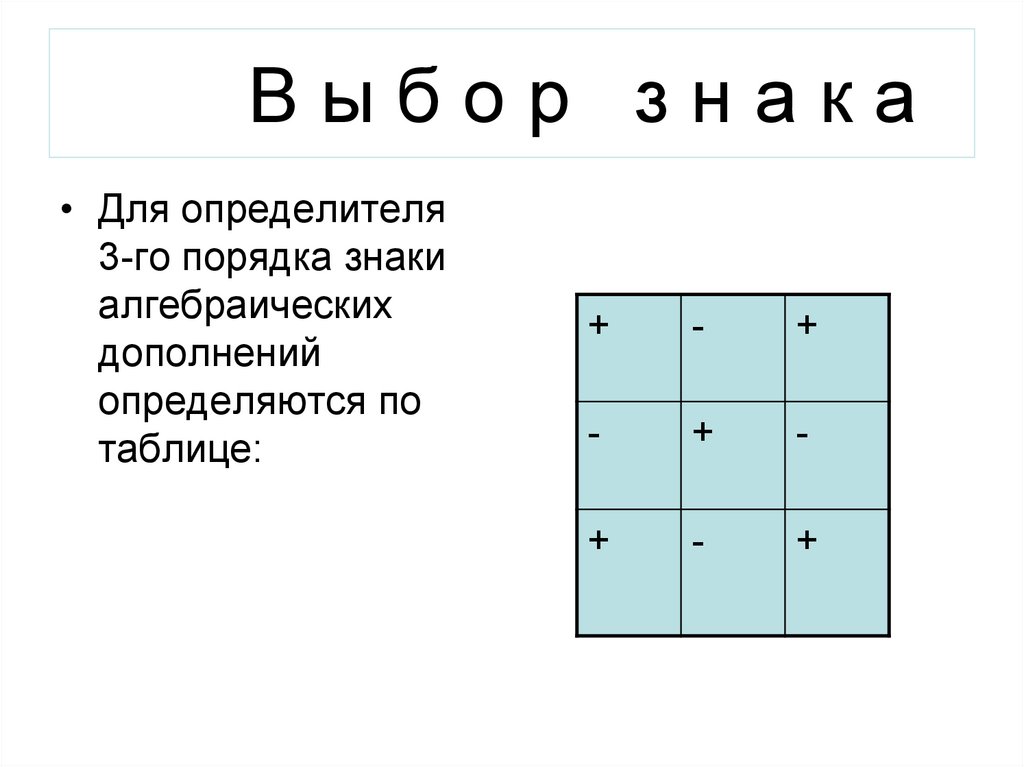
Выбор знака
• Для определителя
3-го порядка знаки
алгебраических
дополнений
определяются по
таблице:
+
-
+
-
+
-
+
-
+

9. теорема разложения

Определитель 3-го порядка равен
сумме парных произведений
элементов какого-либо ряда
определителя на их алгебраические
дополнения (под рядом понимается
строка или столбец)

10. Теорема разложения (продолжение)

Таким образом,
разложений:
имеет
место
a11 A11 a12 A12 a13 A13 ,
a 21 A21 a 22 A22 a 23 A23 ,
a 31 A31 a 32 A32 a 33 A33 ,
a11 A11 a 21 A21 a 31 A31 ,
a12 A12 a 22 A22 a 32 A32 ,
a13 A13 a 23 A23 a 33 A33 .
шесть

11. Свойства определителей

1.Определитель не меняет своего
значения при замене каждой строки
соответствующим столбцом.
2.Определитель изменит знак ,если
поменять местами любые две
строки или столбца.

12. Свойства определителей(продолжение)

3.Общий множитель элементов
какого-либо ряда определителя
можно выносить за знак
определителя.

13. Свойства определителей (продолжение)

4.Определитель равен нулю, если он
имеет два одинаковых столбца или
строки.
5.Определитель равен нулю, если он
имеет нулевой ряд.

14. Свойства определителей (продолжение)

6.Значение определителя
не
изменится, если к элементам строки
или столбца прибавить
соответствующие элементы другой
строки или столбца, умноженные на
одно число.

15. Определители высших порядков

Выражение
a11
a12
a13
a14
a 21
a 22
a 23
a 24
a 31
a 32
a 33
a 34
a 41
a 42
a 43
a 44
a 22
a 23
a 24
a 21
a 23
a 24
a11 a 32
a 33
a 34 a12 a 31
a 33
a 34
a 42
a 43
a 44
a 43
a 44
a 21
a 22
a 24
a 21
a 22
a 23
a13 a 31
a 32
a 34 a14 a 31
a 32
a 33
a 41
a 42
a 44
a 42
a 43
a 41
называется определителем 4-го
порядка
a 41

16. Метод приведения к треугольному виду

Метод приведения к треугольному
виду заключается в таком
преобразовании данного
определителя, когда все элементы
его, лежащие по одну сторону одной
из его диагоналей, становятся
равными нулю.

17. Матрицы

Матрицей называется прямоугольная
таблица чисел .
Если матрица содержит m строк и n
столбцов, то говорят, что матрица имеет
размерность
m n .
17

18. Матрицы

Матрица размера m m называется
квадратной.
Две матрицы считаются равными, если
равны их размеры и равны элементы,
стоящие на одинаковых местах.
18

19. Матрицы

Квадратная матрица называется
невырожденной (неособенной), если
её определитель отличен от нуля, и
вырожденной (особенной) , если
определитель её равен нулю.
19

20. Матрицы

Определитель произведения квадратных
матриц
равен
произведению
определителей
этих матриц:
det( A B) det A det B
20

21. Действия над матрицами.

Суммой двух матриц одинаковой
размерности А и В
называется матрица С той же
размерности,
элементы которой равны суммам
элементов матриц A и B с
одинаковыми индексами.
21

22. Действия над матрицами (продолжение)

Произведением матрицы
на
число называется матрица ,
получающаяся из матрицы A
умножением всех её элементов
на .
22

23. Действия над матрицами (продолжение)

Разностью двух
матриц А и В
одинаковой
размерности
называется матрица A+(-B).
23

24. Действия над матрицами (продолжение)

Произведением матрицы A (aij ) размера
m n на матрицу B (bij ) размера n k
называется матрица C (cij ) размера
m k , элемент cij которой ,
24

25. Действия над матрицами (продолжение)

стоящий в i-ой строке и j-ом
столбце, равен сумме произведений
элементов i-ой строки матрицы A и
соответствующих элементов j-го столбца
матрицы B.
25

26. ИЗОБРАЖЕНИЕ МАТРИЦЫ

a11 a12
a 21 a 22
A
a
a
m
1
m2
a1n
a 2n
a mn
26

27. Обратная матрица

Две невырожденные квадратные
матрицы одного и того же порядка
называются обратными, если их
произведение, взятое в любом
порядке, равно единичной матрице
того же порядка.
27

28. Формула обратной матрицы

.
А11 А21 А31
А11 А21 А31
1
1 А12 А22 А32
А
А12 А22 А32
А
А
А
А13 А23 А33
13 23 33
28

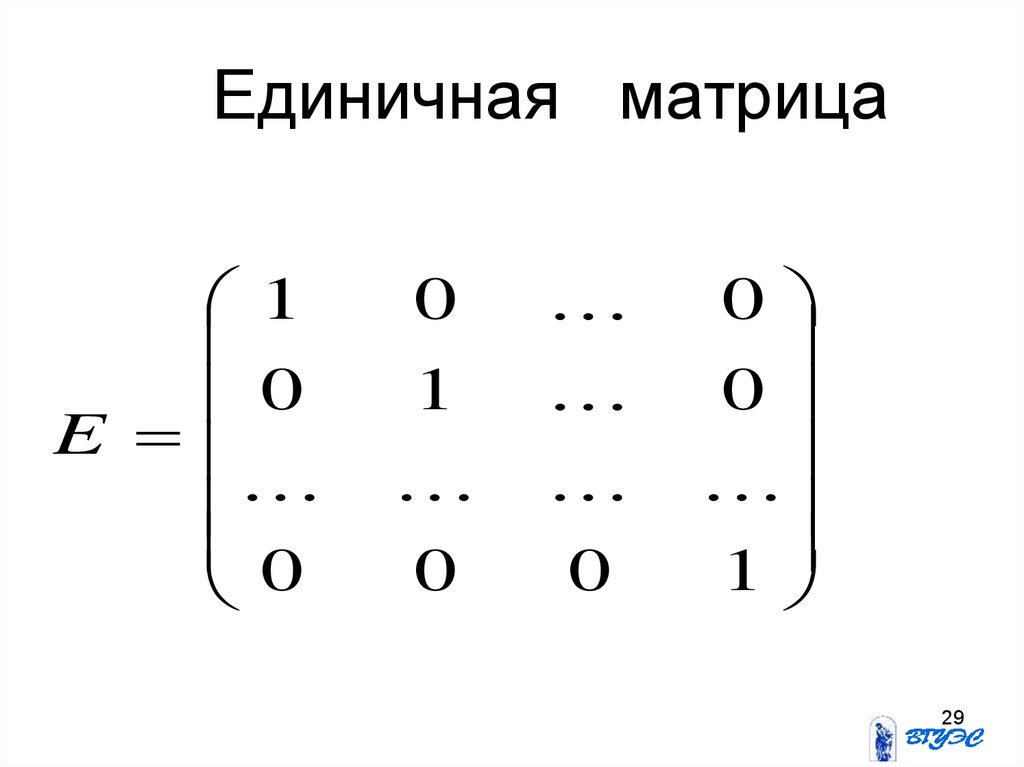
29. Единичная матрица

1
0
E
0
0
1
0
0
0
0
1
29

30. Свойства операций над матрицами

1.A+B=B+A
2.(A+B)+C=A+(B+C)
3.(A+B)k=kA+kB
30

31. Свойства операций над матрицами (продолжение)

4. (AB)C=A(BC)
5. A(B+C)=AB+AC
6. A+O=A
7. AE=EA=A
31

32. Метод Крамера

М е Метод
т о д Крамера
Крамера
а11 a12
а21 a22
... ...
аn1 an 2
... a1n
... a2 n
.
... ...
... ann
b1
b2
1
...
bn
a12
a22
...
an 2
... a1n
... a2 n
.
... ...
... ann
1
x1
.
32

33. М е т о д К р а м е р а

Метод
Крамера
Аналогично находят остальные
переменные по формулам:
n
xn .
33

34. Правило Крамера решения квадратных систем линейных равнений

Если определитель матрицы A не
равен нулю, то система имеет
единственное решение,
определяемое формулами:
1
x1
Здесь i – определитель n-го
порядка,
получающийся
из
x 2
определителя матрицы A
2
коэффициентов системы заменой
i-го столбца столбцом свободных
членов.
x n
n
34